2.3 Transport de l’électricité
L’énergie électrique ne pouvant être stockée qu’en petite quantité et à des coûts importants, il est nécessaire de la produire « en continu ». Mais les lieux de production ne sont pas forcément les lieux où elle est utilisée.
Effet Joule et perte d’énergie électrique
- Faire un schéma d’un circuit électrique modélisant une ligne à haute tension.
- Utiliser les formules littérales reliant la puissance à la résistance, l’intensité et la tension pour identifier l’influence de ces grandeurs sur l’effet Joule.
Effet Joule
L’effet Joule, vous connaissez depuis longtemps. C’est le fait que, lorsqu’un courant électrique circule dans un conducteur, celui-ci s’échauffe. Une partie de l’énergie électrique transportée est alors transformée en chaleur.
Il arrive parfois que l’on souhaite utiliser cet effet : tous les appareils électriques qui servent à chauffer l’utilisent (chauffe-eau, bouilloire électrique, radiateur, etc…). Mais la plupart du temps, l’effet Joule est un effet indésirable du passage du courant, car il constitue une perte d’énergie.
Loi d’Ohm et puissance électrique
Pour bien suivre ce chapitre, gardez à l’esprit les deux formules ci-dessous :
Loi d’Ohm
Pour un conducteur ohmique de résistance électrique $*R*$, la tension à ses bornes $*U*$, et l’intensité du courant qui le traverse $*I*$ sont liés par la relation : $µ U=R·I µ$ Un fil électrique est un conducteur ohmique (bien que sa résistance soit relativement faible).
Puissance électrique
Pour un dipôle électrique (un générateur, un moteur, une ampoule, un conducteur ohmique, bref… tous les dipôles) parcouru par un courant d’intensité $*I*$ et aux bornes duquel il y a une tension $*U*$, la puissance électrique $*P*$ produite ou consommée vaut : $µ P=U·I µ$
Comme un conducteur ohmique obéit à la loi d’Ohm, la puissance électrique qu’il consomme (et qui est donc transformée en chaleur par effet Joule) peut s’écrire :
Puissance dissipée par effet Joule
$µ P_J = U·I = (RI)·I = RI^2 µ$ ou encore $µ P_J = U· \frac UR = \frac{U^2}R µ$Transport d’énergie électrique sous haute-tension

Pour vous faire comprendre l’intérêt de la haute tension dans le transport du courant, voici un petit exercice.
Haute tension
Imaginons un dipôle électrique D qui a besoin d’une puissance électrique de 100 W. Ce dipôle est connecté à un générateur par l’intermédiaire de deux fils ayant chacun une résistance électrique de 1 Ω.
Ce circuit pourrait modéliser une ville (le dipôle D), une centrale électrique (le générateur) et les câbles reliant la ville à la centrale.
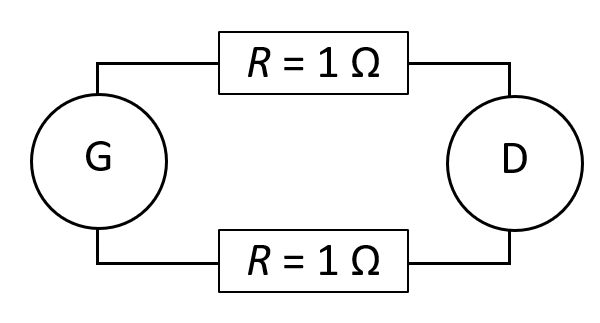
1. Si la tension aux bornes de D vaut 10 V, quelle doit être l’intensité le traversant s’il concomme une puissance de 100 W ?
2. Quelle va être la puissance thermique dissipée par les câbles par effets Joule ?
3. Quelle sera la puissance électrique que devra produire la centrale pour que D reçoivent bien ses 100 W ? Commentez ce résultat.
4. Mêmes questions (1 à 3) si le dipôle D est alimenté avec une tension de 100 V.
5. Conclure quant à l’intérêt de la haute tension pour le transport du courant.
Correction
1. $*I = \frac PU =*$ 10 A
2. $*P_J = 2×RI^2 =*$ 200 W
3. Le générateur devra produire 300 W, soit le triple (!) de ce qui est nécessaire.
4. $*I = \frac PU =*$ 1 A ; $*P_J = 2×RI^2 =*$ 2 W. Le générateur devra produire 102 W pour 100 W consommés.
5. Le transport sous haute-tension est bien plus efficace en terme de perte électrique.
Réseaux de transport
- Modéliser un réseau de distribution électrique simple par un graphe orienté. Exprimer mathématiquement les contraintes et la fonction à minimiser.
- Sur l’exemple d’un réseau comprenant uniquement deux sources, un nœud intermédiaire et deux cibles, formuler le problème de minimisation des pertes par effet Joule et le résoudre pour différentes valeurs numériques correspondant aux productions des sources et aux besoins des cibles.
Qu’est-ce qu’un graphe ?
Un réseau de transport et de distribution d’énergie électrique peut être modélisé par un circuit électrique d’un point de vue physique, mais cette modélisation devient vite inutilement compliquée lorsqu’il s’agit de modéliser un réseau un peu complexe uniquement d’un point de vue échange d’énergie.
Lorsqu’on cherche à modéliser mathématiquement un tel réseau, on fait appel à un objet mathématique appelé graphe. Un graphe peut d’ailleur servir à modéliser tout un tas d’autres choses : réseaux sociaux, réseaux informatique, réseaux routier… Mais ce n’est pas notre propos ici.
Voici la définition qu’en donne Wikipédia :
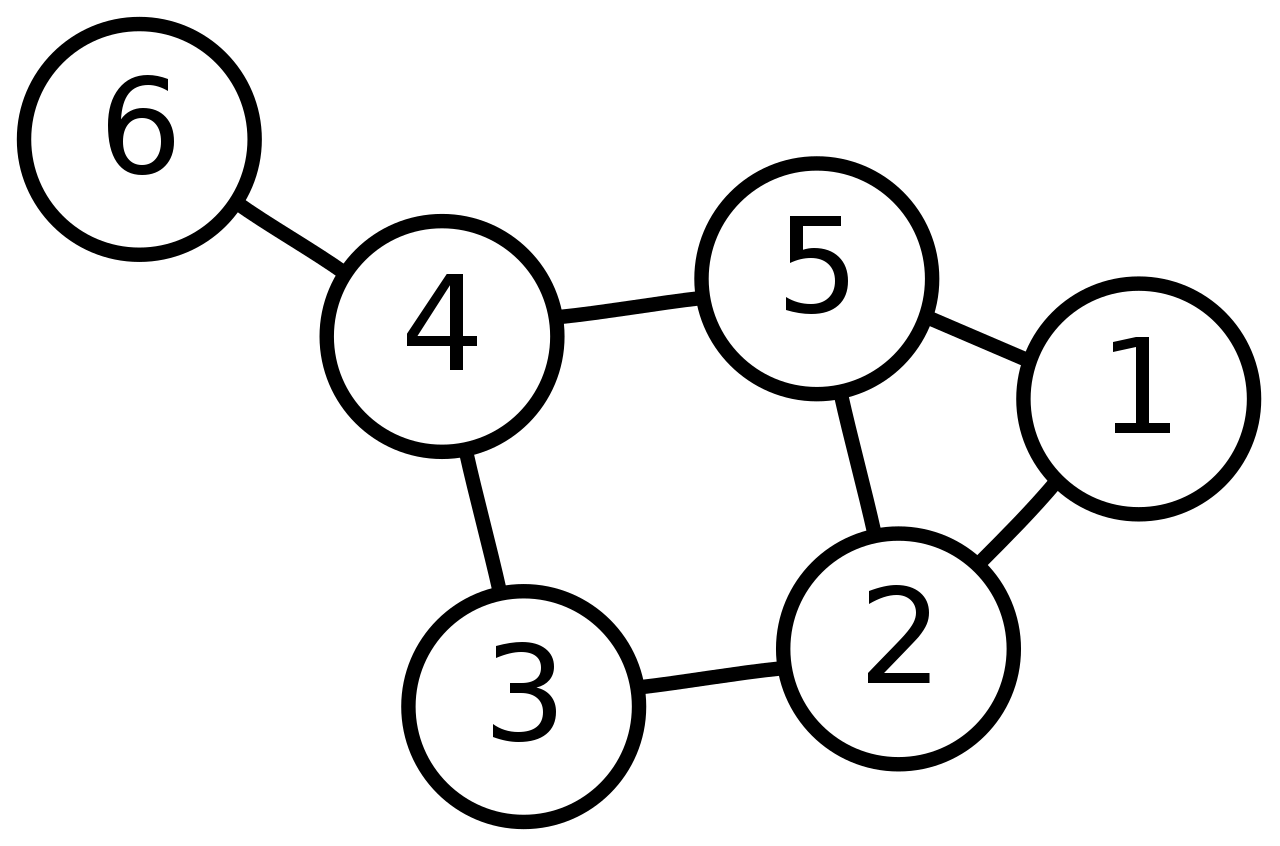
Modélisation d’un réseau de transport
Le réseau électrique d’un pays est constituée de plusieurs sources d’énergie électrique (des centrales thermiques, barrages, etc.), de transformateurs capables de recevoir de l’énergie électrique de différentes sources et de la redistribuer sous la tension voulue (en général 230 V, mais ici, on s’en fiche) et d’un grand nombre de récepteurs qui consomment cette énergie électrique (usine, habitations, etc) qui peuvent parfois être connectée entre eux.
On peut modéliser ce réseau par un graphe, avec autant de nœuds qu’il y a de sources, de transformateurs et de récepteurs, et plein d’interconnexions, qui sont les arrêtes du graphe. Certaines sont orientées (l’énergie électrique quitte les sources) et d’autres non (les transformateurs peuvent recevoir ou donner de l’énergie électrique par la même connexion, selon les besoins locaux).
La problématique constante qui se pose aux ingénieurs en charge de ce réseau est :
Oui, c’est vrai, mais (1) dans la vie, rien n’est simple et (2) les gars sont ingénieurs, tout de même… Et puis, je n’ai pas dit qu’on allait résoudre ce problème 😉
Le problème de la minimisation des pertes
Ah ben si, en fait ! 😅 Mais dans un cas très simple seulement.
Imaginons deux villages, alimentés en énergie électrique par deux sources. Ces deux sources sont aussi polluantes l’une que l’autre donc on ne va pas tenir compte du critère environnemental dans ce problème (c’est d’ailleurs une habitude en politique, mais c’est une autre histoire… 😏). Un transformateur central reçoit l’énergie électrique des deux sources.
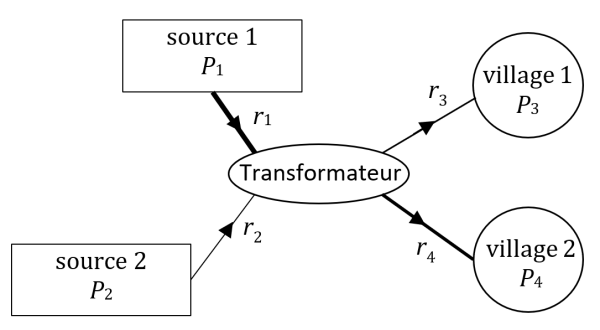
Pour la suite du problème, on va travailler avec des valeurs simples qui n’ont pas de pertinence physique et on va oublier les unités. L’idée est d’arriver à trouver une méthode pour résoudre le problème de la minimisation des pertes par effet Joule.
Les $*r_i*$ représentent la résistance des câbles.
Le village 2 consomme une puissance $*P_4*$ = 3.
La connexion $*r_1*$ est bonne : $*r_1*$ = 1
La connexion $*r_2*$ est mauvaise car la source 2 est loin : $*r_2*$ = 3
La connexion $*r_3*$ est moyenne : $*r_3*$ = 2
La connexion $*r_4*$ est bonne : $*r_4*$ = 1
Le transformateur ne dissipe pas d’énergie.
L’énergie dissipée par effet Joule est négligeable devant les énergies échangées, c’est-à-dire qu’on peut faire l’approximation que l’énergie produite par les sources est égale à l’énergie reçue par les villages.
On suppose que les deux sources d’énergie électrique ne sont pas limitées en puissance.
Formulation du problème
Sachant que les pertes lors du passage dans les câbles sont proportionnelles à la valeur de leur résistance $*r_i*$ et au carré de la puissance qu’ils transportent (voir l’encadré ci-contre / ci-dessous), quelle doit être la valeur des puissances $*P_1*$ et $*P_2*$ produites par les sources pour avoir le minimum de perte possible ?
Suggestion : vous pouvez commencer par calculer les pertes par effet Joule pour différentes valeurs de $*P_1*$ comprises entre 0 et 5 (en vous aidant d’un tableur), puis tracer le graphique montrant les pertes en fonction de $*P_1*$.
Remarque : la résolution formelle de ce problème ne dépasse pas le niveau première. Pour ceux qui n’ont pas fait de spé math l’année dernière, vous pouvez vous aider d’un tableur. Dans ce cas, le problème ne dépasse pas le niveau collège.
La solution
On commence par recenser les pertes dans chaque câble/connexion :
Connexion $*r_1*$ : $*k·r_1·P_1^2*$
Connexion $*r_2*$ : $*k·r_2·P_2^2*$
Connexion $*r_3*$ : $*k·r_3·P_3^2*$
Connexion $*r_4*$ : $*k·r_4·P_4^2*$
L’énergie totale dissipée $*E_D*$ pendant le transport est donc proportionnelle à : $µ r_1·P_1^2 + r_2·P_2^2 + r_3·P_3^2 + r_4·P_4^2 µ$
En remplaçant les grandeurs connues par leur valeurs, on obtient que $*E_D*$ est proportionnelle à : $µ P_1^2 + 3P_2^2 + 2×2^2 + 1·3^2 µ$
Les inconnues sont $*P_1*$ et $*P_2*$.
Comme l’énergie produite est égale à l’énergie consommée (les pertes sont négligeables par rapport à l’énergie consommée), on sait donc que $*P_1 + P_2 =*$ 5
On peut donc écrire, en tenant compte que $*P_1 = 5 - P_2*$ : $µ \begin{aligned} E_D &\propto (5 - P_2)^2 + 3P_2^2 + 8 + 9 \\ E_D &\propto 25 - 10P_2 + P_2^2 + 3P_2^2 + 17 \\ E_D &\propto 4P_2^2 - 10P_2 + 42 \\ \end{aligned} µ$
Ne pas perdre de vue notre objectif, à savoir : quelles valeurs doivent avoir $*P_1*$ et $*P_2*$ pour minimiser $*E_D*$ ?
Pour cela, il suffit de chercher pour quelle valeur de $*P_2*$ la dérivée de $*E_D*$ par rapport à $*P_2*$ : $µ (E_D)' \propto 8P_2-10 µ$
Donc $*E_D*$ est minimal pour $*8P_2-10 =0*$ soit $*P_2*$ = 1,25 et donc $*P_1*$ = 3,75.
Et voilà ! Retenez que pour rechercher un extremum d’une fonction, il suffit de trouver où sa dérivée s’annule.