P1. Interactions électrique & gravitationnelle
Il y a, dans l’Univers, quatre interactions fondamentales. L’interaction gravitationnelle, qui est le fait que deux masses s’attirent, l’interaction électrique, qui est le fait que deux charges s’attirent ou se repoussent selon leur signe, et enfin deux autres interactions (l’interaction nucléaire forte et l’interaction nucléaire faible) qui ne jouent un rôle qu’à l’échelle des nucléons.
Électrisation de la matière
- Interpréter des expériences mettant en jeu l’interaction électrostatique.
- Illustrer l’interaction électrostatique.
- Mettre en œuvre un dispositif permettant d’illustrer l’interaction électrostatique.
D’abord, un bref rappel de ce que vous avez déjà vu au collège et en seconde, ça ne fera pas de mal ! 😊
Certaines particules possèdent une caractéristique particulière appelée charge électrique. Il existe deux types de charge électrique : positive et négative.
Deux charges de même signe se repoussent ; deux charges de signe opposé s’attirent.
Il est possible de charger certaines matières, en lui arrachant des électrons ou en lui donnant des électrons.
Dans un matériau conducteur (comme un métal), les électrons peuvent se déplacer librement.
Place maintenant à quelques expériences sur l’électrisation.
TP Électrisation et interaction électrostatique

Objectif : découvrir le phénomène d’électrisation.
Quelques expériences à interpréter
Pour chacune des expériences ci-dessous, proposer une explication qui permette de rendre compte de ce que vous observez.
- Frotter l’une après l’autre deux pailles contre un morceau de tissu. Approcher ensuite les deux pailles l’une de l’autre. Attention : le phénomène n’est pas facile à observer. Poser une des deux pailles en équilibre sur un rebord de table, perpendiculairement à celui-ci par exemple, de manière à ce qu’elle puisse pivoter très facilement. Approcher ensuite l’autre paille.
- Frotter une baguette en verre contre un morceau de tissu. Approcher ensuite la baguette de la paille.
- Frotter une paille avec du tissu et une autre avec du papier absorbant. Approcher ensuite les deux pailles l’une de l’autre.
- Approcher la paille chargée d’une petite boule d’aluminium suspendue.
- Approcher la baguette de verre chargée de la boule d’aluminium.
- Expériences d’électrisation avec la machine de Wimshurst (réalisées par le professeur).
- Charger une paille en la frottant avec du tissu. Approchez-la d’un filet d’eau.
- Faites la même expérience avec une baguette de verre.
Électrisation par frottement
En frottant deux matières différentes, il est possible, pour certaines combinaisons de matières, de les charger. Une des matières arrache des électrons à l’autre. La première se charge négativement et la deuxième se charge positivement.
Bonne question ! À laquelle on ne vous demandera jamais de répondre. 😊
Il faut pour cela consulter une série triboélectrique ou le déterminer par l’expérience.
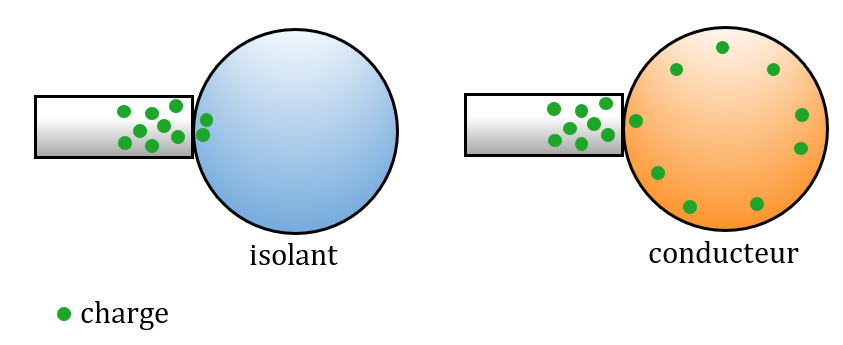
Électrisation par contact
Un objet chargé mis en contact avec un objet neutre lui transmet une partie de sa charge.
Si l’objet touché est constitué d’un matériau conducteur, alors les charges transmises se répartissent dans tout l’objet.
Si l’objet touché est constitué d’un matériau isolant, alors les charges transmises restent dans la zone de contact.
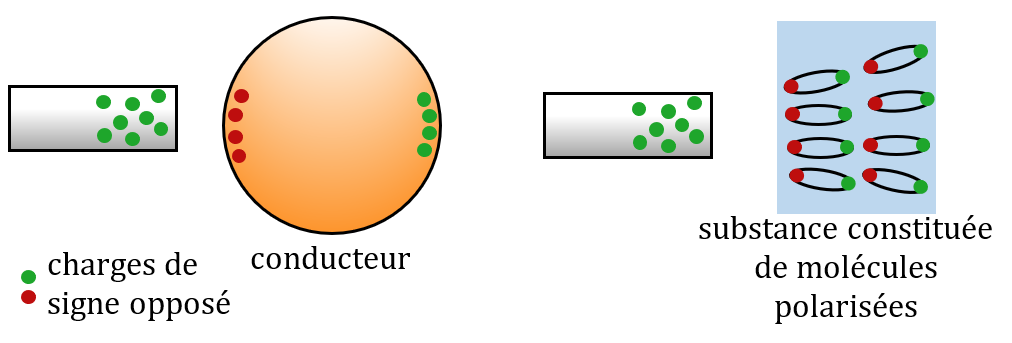
Électrisation par influence
Lorsqu’on approche un objet chargé d’un conducteur, la répartition des charges est modifiée.
Lorsqu’on approche un objet chargé d’un liquide dipolaire (l’eau par exemple), les dipôles s’orientent de manière à présenter leur charge opposée à celle de l’objet chargé.
Cloche de Franklin
Benjamin Franklin a inventé une cloche qui sonne toute seule lorsqu’un orage approche. Lorsqu’un orage se prépare, des nuages chargés négativement s’accumulent. Ces charges négatives dans les nuages repoussent les charges négatives du sol dans les profondeurs, laissant la surface du sol chargée positivement. Cette cloche est schématisée ci-dessous.
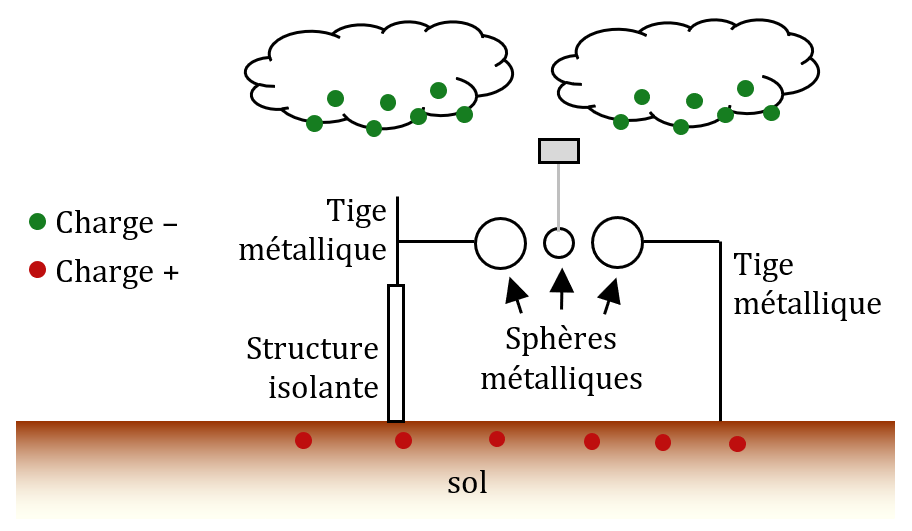
La sphère métallique du milieu peut osciller jusqu’à venir en contact avec chacunes des deux autres sphères.
• Expliquer comment un tel dispositif peut se mettre à « sonner » à l’approche d’un orage.
• Quel danger présente-t-il ?
Correction
Les électrons de la tige de gauche sont repoussés par les charges négatives portées par les nuages. Ils s’accumulent dans la sphère de gauche, qui se charge (légèrement) négativement.
Les électrons de la boule de droite sont attirés par les charges positives du sol (la boule et le sol sont reliés par un conducteur). Le boule de droite se charge donc positivement.
La boule du milieu va donc se polariser et être attirée par l’une au l’autre boule. Au moment du premier contact avec l’une des deux boules chargées, la boule de milieu va également se charger et sera repoussée par la boule avec qui elle vient d’entrer en contact et attirée par l’autre boule. Le phénomène se répète et cela va provoquer un son à chaque contact (phénomène vu en TP).
L’inconvénient de ce dispositif est que les tiges métalliques attirent la foudre.
Les éclairs, lors d’un orage sont une manifestation à la fois courante et spectaculaire du phénomène d’électrisation.
Force gravitationnelle et force électrique
- Utiliser la loi de Coulomb.
- Utiliser les expressions vectorielles de la force de gravitation et de la force électrostatique.
- Citer les analogies entre la loi de Coulomb et la loi d’interaction gravitationnelle.
L’interaction gravitationnelle et l’interaction électromagnétique sont deux des quatre interactions fondamentales de l’Univers.
L’interaction entre deux objets est modélisée par une force, représentée par un vecteur ayant 4 caractéristiques : direction ; sens ; norme (ou valeur) ; point d’application.
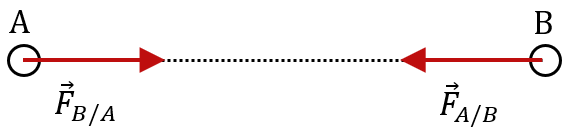
Interaction gravitationnelle
L’interaction gravitationnelle, c’est le fait que deux masses s’attirent l’une l’autre. Cette interaction est responsable de la structure de l’Univers entier à l’échelle macroscopique : la Terre, ainsi que le Soleil et les autres planètes se sont formés grâce à l’interaction gravitationnelle. Notre système solaire doit sa structure et sa stabilité à l’interaction gravitationnelle. De même que l’existence des galaxies et des amas de galaxies. Bref, si l’Univers a la structure qu’il a, c’est à cause de la gravitation.

Deux objets A et B exercent l’un sur l’autre une force attractive appelée force d’attraction gravitationnelle.
| $µ F_{A/B} = F_{B/A} = {Gm_Am_B \over d^2} µ$ | $*G*$ : constante de gravitation universelle – 6,67×10-11 S.I. $*m_A*$ et $*m_B*$ : masse des objets en interaction (kg) $*d*$ : distance séparant le centre des deux objets (m) $*F_{A/B}*$ et $*F_{B/A}*$ : valeur des forces, en newton (N) |
Le vecteur représentant la force d’attraction gravitationnelle a pour direction la droite passant par le centre de A et le centre de B.
Son sens rend compte du fait que cette force est toujours attractive.
Son point d’application est le centre des deux objets.
Expression vectorielle de la force gravitationnelle
Pour écrire l’expression vectorielle de la force gravitationnelle qui s’exerce entre deux corps, on définit un vecteur unitaire $*\vec{u}*$ de direction la droite (AB) et on lui attribue un sens (peu importe lequel).
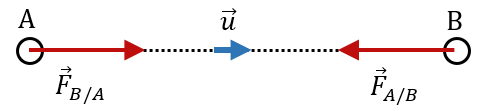
Dans le sens choisi pour cet exemple : \[\begin{aligned} \vec{F}_{B/A} &= {Gm_Am_B \over d^2}\vec{u} \\ \vec{F}_{A/B} &= -{Gm_Am_B \over d^2}\vec{u} \end{aligned}\]
Force gravitationnelle de la Terre
Données
- Masse de la Terre : $*M_T*$ = 6,0·1024 kg
- Masse du Soleil : $*M_S*$ = 2,0·1030 kg
- Rayon de la Terre : $*R_T*$ = 6380 km
- Distance Terre-Soleil : $*D_{TS}*$ = 150·106 km (de centre à centre)
1.a. Donner l’expression de l’intensité $*F*$ de la force gravitationnelle exercée par la Terre sur une masse $*m*$ en fonction de l’altitude $*z*$ de cette masse par rapport au niveau de la mer.
1.b. Calculer la force exercée par la Terre sur l’objet lorsque celui-ci est à sa surface en prenant comme masse de l’objet $*m*$ = 1,0 kg.
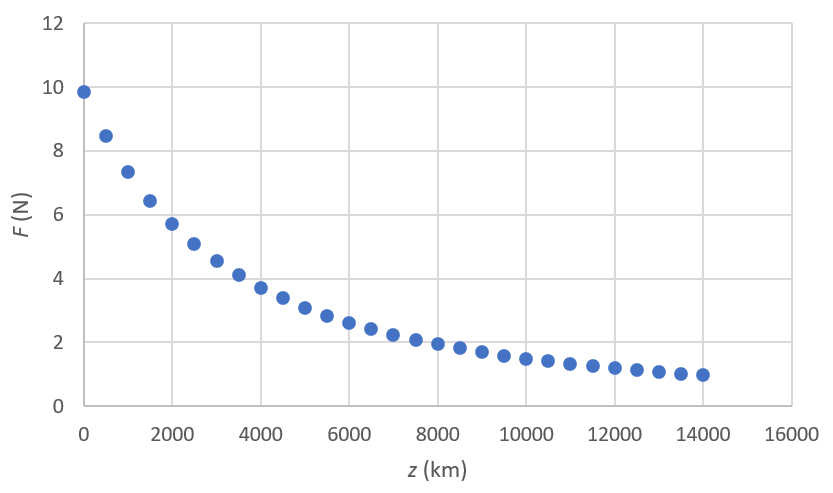
1.c. En utilisant un tableur, représenter cette force sur un graphique pour une altitude allant de 0 à 14 000 km (un point tout les 500 km). Vous prendrez $*m*$ = 1 kg.
On dit qu’une sonde interplanétaire a quitté la zone d’influence gravitationnelle de la Terre lorsque la force exercée par le Soleil sur celle-ci est supérieure à celle exercée par la Terre.
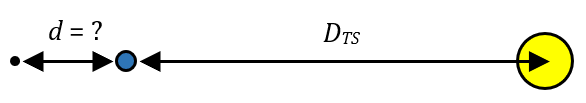
2.a. Représenter sur un graphique l’évolution de ces deux forces en fonction de la distance de l’engin au centre de la Terre ($*d*$) et du Soleil, dans la situation ci-schématisée ci-dessus. On prendra une masse $*m*$ = 1 kg.
Trouver graphiquement à quelle distance du centre de la Terre la sonde quitte la zone d’influence de la Terre.
2.b Retrouver cette distance par le calcul.
Correction
1.a. $* F= \dfrac {GM_Tm}{(R_T + z)^2} *$
1.b. N’oubliez pas de convertir $*R_T*$ en mètres. $µ F = \frac {GM_Tm}{R_T^2} = \frac {6,67·10^{-11}×6,0·10^{24}×1}{(6,380·10^6)^2} µ$ $*F*$ = 9,83 N
1.c. Graphique de $*F = f(z)*$
2.a. Graphique obtenu sur Excel :
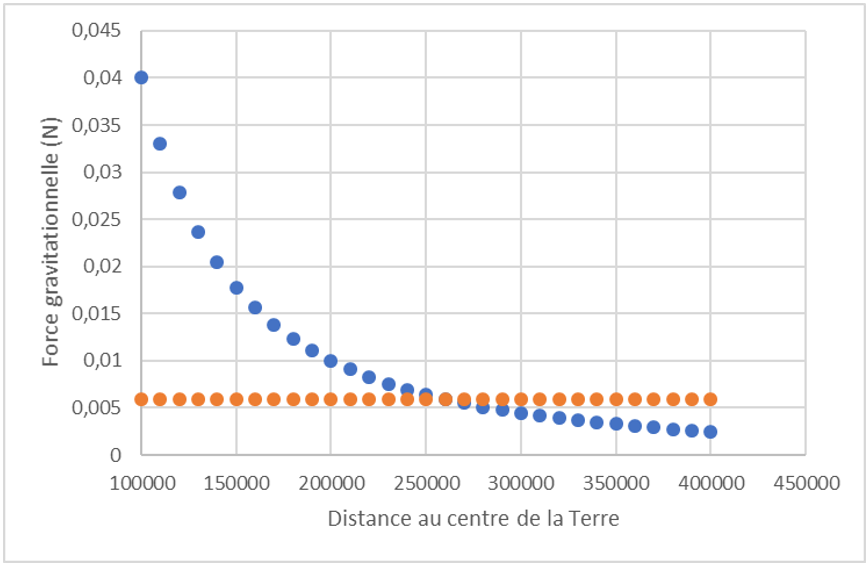
En bleu : force exercée par la Terre sur une masse de 1 kg.
En orange : force exercée par le Soleil, sur une masse de 1 kg.
On observe que la limite de la zone d’influence gravitationnelle de la Terre se situe vers 255.000 km.
2.b. Limite de la zone d’influence gravitationnelle de la Terre : on cherche à calculer pour quelle distance $*d*$ entre la sonde et le centre de la Terre la valeur de la force gravitationnelle $*F_T*$ est égale à la valeur de la force gravitationnelle exercée par le soleil $*F_S*$. On a : $µ F_T = {GM_Tm \over d^2} \text{ et } F_S = {GM_Sm \over {(D_{TS} + d)}^2} µ$ On cherche pour quelle valeur de $*d*$ ces deux forces sont égales : $µ \begin{aligned} {GM_Tm \over d^2} &= {GM_Sm \over {(D_{TS} + d)}^2} \\ {M_T \over d^2} &= {M_S \over {(D_{TS} + d)}^2} \\ {M_T \over M_S} &= {d^2 \over {(D_{TS} + d)}^2} \\ {d \over {D_{TS} + d}} &= \sqrt{M_T \over M_S} \\ \end{aligned} µ$
Par commodité, notons $*\alpha*$ le terme $*\sqrt{M_T \over M_S}*$
$µ \begin{aligned}d &= \alpha·(D_{TS} + d) \\ d( 1-\alpha) &= \alpha·D_{TS} \\ d &= {\alpha \over {1-\alpha }}·D_{TS} \end{aligned} µ$ Application numérique : $* d \approx *$ 260·103 km
Interaction électromagnétique
Deux charges électriques ponctuelles $*q_A*$ et $*q_B*$ exercent l’une sur l’autre une interaction qui peut être répulsive (charges de même signe, vecteurs en bleu) ou attractive (charges de signe opposé, vecteurs en rouge).

| $µ F_{A/B} = F_{B/A} = {k|q_A·q_B| \over d^2} µ$ |
$*k*$ : 8,99·109 N·m2·C-2 $*q_A*$ et $*q_B*$ : charge électrique des particules A et B (C) $*d*$ : distance séparant le centre des deux objets (m) $*F_{A/B}*$ et $*F_{B/A}*$ : valeur des forces, en newton (N) |
La relation $* F = {k|q_Aq_B| \over d^2} *$ est appelée la loi de Coulomb.
Le vecteur représentant la force électrique a pour direction la droite passant par le centre de A et le centre de B.
Son sens dépend du caractère attractif ou répulsif de l’interaction.
Son point d’application est le centre des deux objets.
Cohésion de l’atome d’hydrogène
L’électron d’un atome d’hydrogène reste à proximité du proton qui constitue son noyau car il est attiré par celui-ci.
Cette attraction est-elle majoritairement due à leur charge opposée ou à leur attraction gravitationnelle ?
Données
- Masse du proton : $*m_p*$ = 1,67·10-27 kg
- Masse de l’électron : $*m_e*$ = 9,11·10-31 kg
- Charge élémentaire : $*e*$ = 1,60·10-19 C
- Distance moyenne proton-électron dans l’atome d’hydrogène : $*d*$ = 5·10-11 m
Correction
Force gravitationnelle entre un électron et un proton : $* F_g \approx *$ 4,1·10-47 NForce électrique entre un électron et un proton : $* F_e \approx *$ 9·10-8 N
On remarque que la force électrique est environ 1039 fois plus grande (!) ce qui signifie que l’attraction gravitationnelle ne joue aucun rôle dans la cohésion de l’atome d’hydrogène.
Analogies entre l’interaction gravitationnelle et l’interaction électromagnétique
Remarquez la similarité entre les expressions des deux forces.
$µ {Gm_Am_B \over d^2} \quad \text{et} \quad {k|q_Aq_B| \over d^2} µ$
Dans les deux cas, la valeur de la force est proportionnelle au produit des masses/charges sur la distance qui les sépare, au carré. Bien-sûr, les constantes de proportionnalité – $*G*$ dans un cas et $*k*$ dans l’autre – n’ont pas du tout la même valeur. De plus, comme une charge peut être négative ou positive, au contraire d’une masse, et que l’on parle de la valeur de la force, qui est forcément positive, il faut donc éliminer un éventuel signe - au produit $*q_Aq_B*$, d’où la présence des barres de valeur absolue.
Champ gravitationnel et champ électrique
- Utiliser les expressions vectorielles du champ de gravitation et du champ électrostatique.
- Caractériser localement une ligne de champ électrostatique ou de champ de gravitation.
- Cartographier un champ électrostatique.
Champ gravitationnel
Imaginons une planète de masse $*M*$ et un objet de masse $*m*$ situé à une distance $*d*$ du centre de cette planète.
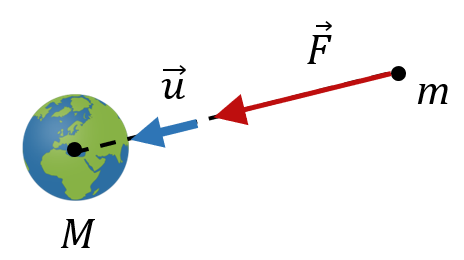
Nous avons vu que la planète exerce sur l’objet une force :
$µ \vec{F} = {GMm \over d^2}\vec{u} µ$
On peut écrire l’expression de cette force un peu différemment, mais d’une manière complètement équivalente :
$µ \vec{F} = m·{GM \over d^2}\vec{u} µ$
Vous voyez que $*{GM \over d^2}\vec{u}*$ ne dépend absolument pas de la valeur de la masse $*m*$, mais seulement de la masse de la planète et de la distance à laquelle on se trouve de son centre. Eh bien les physiciens appellent ça le champ gravitationnel de la planète. Il est noté $*\mathcal{\vec{G}}*$. Tous les objets créent autour d’eux un champ gravitationnel. Le concept de champ gravitationnel n’est qu’une autre manière de voir l’interaction gravitationnel entre deux objets.
Du coup, on peut également écrire $*\vec{F}*$ sous la forme $* \vec{F} = m\mathcal{\vec{G}}*$. L’intensité $*\mathcal{G}*$ du champ de pesanteur $*\mathcal{\vec{G}}*$ s’exprime en N·kg-1.
Champ de pesanteur de la Terre
Le poids d’un objet est la force avec laquelle cet objet est attiré vers le centre de la Terre (ou d’une autre planète). Le poids est la somme de la force d’attraction gravitationnelle et de la force d’entraînement, dite « force centrifuge », due à la rotation de la Terre qui contribue à diminuer le poids.
Le champ de pesanteur est associé au poids de la même manière que la champ gravitationnel est associé à la force gravitationnelle : il est définit comme
$* \vec{P} = m\vec{g} *$
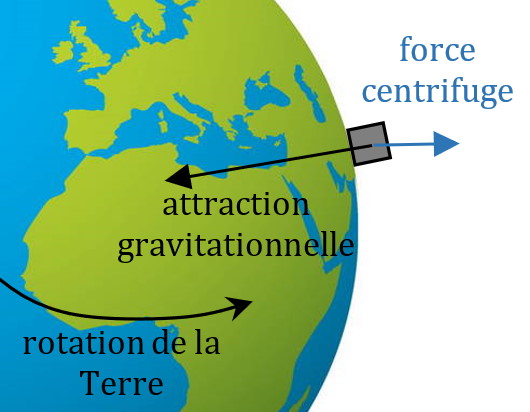
La force centrifuge est faible comparée à la force d’attraction gravitationnelle.
Dans un domaine restreint d’altitude, on peut considérer que sa valeur ne varie pas.
Valeur du champ gravitationnel
Montrer que l’expression de l’intensité du champ gravitationnel $* \mathcal{G} *$ autour d’une planète ou autour d’un objet ponctuel de masse $*M*$ et à une distance $*d*$ de son centre peut s’écrire : $µ \mathcal{G} = {GM \over d^2} µ$
Calculer la valeur de $*\mathcal{G}*$ à la surface de la Terre.
Correction
On sait d’une part que, pour un objet de masse $*m*$ situé à une distance $*d*$ de l’objet en question, la valeur de la force gravitationnelle $*F*$ qu’il subit s’écrit : $µ F = {GMm \over d^2} µ$ D’autre part, d’après la définition du champ gravitationnel, on sait également que : $µ F = m\mathcal{G} µ$ Donc on a l’égalité : $µ m\mathcal{G} = {GMm \over d^2} µ$ En simplifiant par $*m*$, il vient : $µ \mathcal{G} = {GM \over d^2} µ$
Petite application numérique avec les données que vous trouvez dans les exercices précédents : $* \mathcal{G} *$ = 9,83 N·kg-1
Champ électrique
Pour le champ électrique, le principe est le même que pour le champ gravitationnel. Une charge électrique $*Q*$ crée autour d’elle un champ électrique $*\vec{E}*$. Toute charge $*q*$ se trouvant dans ce champ subira une force électrique $* \vec{F}_e = q\vec{E}*$.
L’intensité $*E*$ du champ électrique $* \vec{E}*$ s’exprime en V·m-1.
En revanche, la force électrique $* \vec{F}_e *$ s’appliquant à une charge $*q*$ se trouvant dans un champ électrique aura le même sens que le champ électrique $*\vec{E}*$ seulement si $*q*$ > 0. Elle sera de sens opposé si $*q*$ < 0.
Lignes de champ
Une ligne de champ est une ligne tangente en chacun de ses points au vecteur champ (électrique ou gravitationnel). Elle est orientée par une flèche dans le sens du champ.
Les lignes de champ sont une manière commode de visualiser un champ vectoriel. Elles n’indiquent pas la valeur du champ, mais son orientation.
Ces lignes sont continues et ne se croisent jamais.
Champ électrique autour d’une charge ponctuelle
Le schéma ci-dessous représente un proton p ainsi que deux points P1 et P2 situés à une même distance $*d*$ de p, matérialisée par des pointillés.
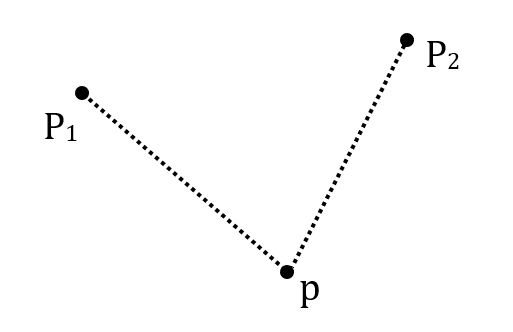
1.a. Exprimer la valeur $*F*$ de la force exercée par p sur un autre proton situé en P1 ou en P2. La charge du proton sera notée $*e*$.
1.b. Représenter ces forces par un vecteur, ainsi que deux vecteur unitaires $*\vec{u}*$ et $*\vec{u}’*$ permettant de donner l’expression vectorielle de $*\vec{F}*$ pour chacune des positions.
1.c. Donner l’expression vectorielle de cette force pour chacune de position.
2.a. En vous servant des résultats précédents, exprimer la valeur du champ électrique créé par p aux points P1 et P2.
2.b. Représenter les vecteurs champs électriques à ces deux endroits.
2.c. Représenter les lignes de champs créées par le proton autour de lui.
3. Reprendre l’exercice dans le cas d’un électron.
Correction
1.a. $*F={ke^2 \over d^2} *$
1.b. Forces et vecteurs unitaires.
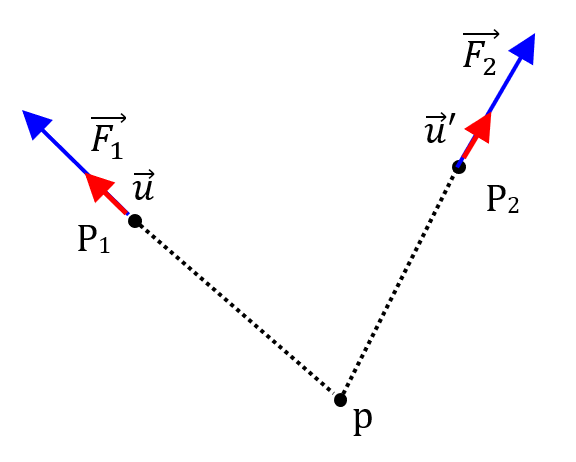
Remarque : on peut représenter les vecteur $*\vec{u}*$ et $*\vec{u}'*$ n’importe où.
2.a. On sait que $* \vec{F} = q\vec{E} *$ donc $* \vec{E} = {\vec{F} \over q} *$, ce qui donne, dans notre situation : $* E = {ke \over d^2} *$.
2.b. Les vecteurs $*\vec{E}_1*$ et $*\vec{E}_2*$ sont colinéaires et ont le même sens que les vecteurs $*\vec{F}_1*$ et $*\vec{F}_2*$
2.c. Les lignes de champs sont tangentes en tout point au champ électrique. Il suffit d’imaginer comment est le champ électrique autour du proton (les deux exemples aux points P1 ou en P2 sont là pour vous y aider) pour en déduire l’organisation des lignes de champs autour du proton. Ces lignes partent toutes du protons et sont orientées vers l’exterieur.
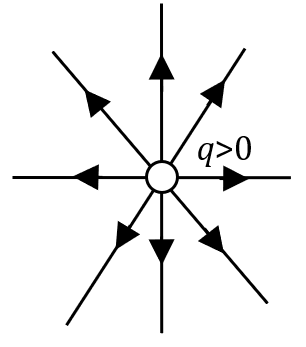
3. Si on remplace le proton par un électron, on change le signe de la charge. Cela revient à inverser le sens des forces qui s’exercent sur le proton placé en P1 et en P2, ainsi que le sens du champ électrique et des lignes de champ.
Révision & entraînement
Cohésion d’un cristal de NaCl
Un cristal de chlorure de sodium est composé d’ions Na+ (en violet) et d’ions Cl– (en vert).
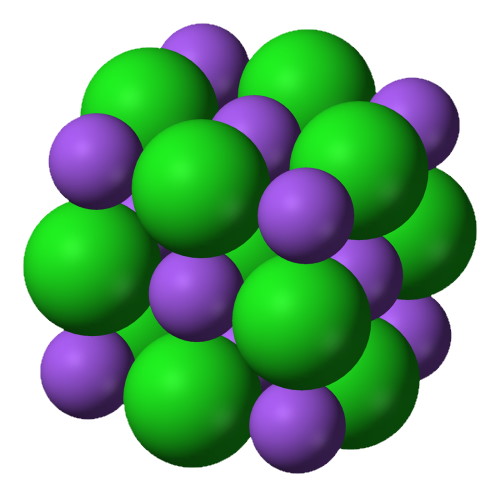
La distance entre deux ions $*\ce{Na+}*$ est la même que la distance entre deux ions Cl– : $*d_1*$ = 0,40 nm. La distance entre un ion $*\ce{Na+}*$ et un ion $*\ce{Cl-}*$ est de $*d_2*$ = 0,28 nm.
1. En assimilant les ions à des corps ponctuels, calculer la valeur des forces s’exerçant entre :
a. Deux ions $*\ce{Na+}*$
b. Deux ions $*\ce{Cl-}*$
c. Un ion $*\ce{Na+}*$ et un ion $*\ce{Cl-}*$.
2. Justifier la cohésion du cristal de chlorure de sodium.
Correction
1.a. Entre deux ions Na+ : $*F = \dfrac {ke^2}{d_1^2}*$ = 1,44·10-9 N (répulsive)
Remarque : $*e*$ est la valeur de la charge élémentaire, soit 1,60·10-19 C. En effet, un ion ayant une charge ⊕ a perdu un électron, donc sa charge est égale à une charge élémentaire. De même, un ion ayant une charge ⊖ a gagné un électron. Donc sa charge est de $*-e*$.
1.b. Entre deux ions Cl– : $*F*$ = 1,44·10-9 N (répulsive)
1.c. Entre un ion Cl– et un ion Na+ : $*F*$ = 2,94·10-9 N (attractive)
2. Les forces de répulsion entre deux ions de même nature sont plus faibles que les forces de répulsion entre des ions de charge opposée, d’où la cohésion du cristal.
Champ de pesanteur de la Terre
Données
- Masse de la Terre : $*M_T*$ = 6,0·1024 kg
- Rayon de la Terre : $*R_T*$ = 6380 km
Poids et force d’attraction gravitationnelle
1. Où sur Terre le poids est-il le plus différent de la force d’attraction gravitationnelle ? Est-il plus important que la force gravitationnel ou plus faible ? Justifier.
Poids et altitude
Dans la pratique, à la surface de la Terre, le poids et l’attraction gravitationnelle sont quasiment égaux. On négligera donc la différence entre ces deux valeurs pour la suite de l’exercice.
2.1. Calculer la valeur de l’intensité du champ de pesanteur à la surface de la Terre.
2.2. Définir un vecteur unitaire $*\vec{u}*$ permettant d’écrire l’expression vectorielle de ce champ gravitationnel en un point P au voisinnage de la Terre. Donner alors cette expression vectorielle.
Correction
1. Le poids est d’autant plus différent de l’attraction gravitationnelle que la force centrifuge est importante. Cette force centrifuge est nulle lorsqu’on se trouve exactement aux pôles géographiques. Elle est d’autant plus forte qu’on se rapproche de l’équateur. C’est donc sur l’équateur que la différence entre le poids et la force d’attraction gravitationnelle est la plus forte.
2.1. $*g = {GM_T \over {R_T}^2} = *$ 9,83 N·kg-1
2.2. Il suffit de choisir un vecteur $*\vec{u}*$ qui pointe vers le centre de la Terre depuis le point P. $µ \vec{g} = {GM_T \over {R_T}^2}\vec{u} µ$
2.3. On a vu dans le cours que l’intensité du champ gravitationnel en un point vaut : $µ{GM \over d^2}µ$ avec $*d*$ la distance entre ce point et le centre de la Terre. Donc $µ g = {GM \over (R_T + z)^2} µ$ avec $*R_T*$ le rayon de la Terre.
À 10 km d’altitude, $*g*$ = 9,80 N·kg-1. Il y a donc environ 0,3 % de diminution.
2.4. On voit que même si on se trouve plus haute que la plus haute montagne sur Terre, l’intensité de la pesanteur varie de moins de 1 %. Donc tant qu’on étudie des situations où l’altitude ne varie pas très fortement, les variations de $*g*$ sont négligeables.
Forces de marées
Extrait de Wikipédia
Lorsqu’un objet attiré par un astre n’est pas considéré comme ponctuel, un côté de cet objet est plus proche de l’astre attracteur que l’autre, et donc n’est pas attiré avec la même force que l’autre. Si cette différence de force est suffisamment forte, cela peut avoir tendance à disloquer l’objet attiré.
Nous allons modéliser un corps humain par deux points associés chacun à une masse de 35 kg et distant de 1 m.
1. Faire un schéma de la situation. Calculer la différence entre les forces gravitationnelles exercées sur ces points pour un être humain se trouvant debout à la surface de la Terre. Conclure.
Dans le film Interstellar, le héros tombe en direction d’un trou noir.
2. Imaginons un trou noir stellaire de 7 masses solaires (7×2·1030 kg). Un tel trou noir aurait un « rayon » de 20 à 60 km environ, selon ce que l’on appelle « rayon » du trou noir – C’est juste une information, vous n’avez pas besoin du rayon pour la suite de l’exercice. Quelle serait la différence entre les forces gravitationnelles exercées sur les deux points de notre modèle, si l’être humain se trouve à une distance de 1000 km du centre d’un tel astre ? Conclure.
Correction
1. Schéma
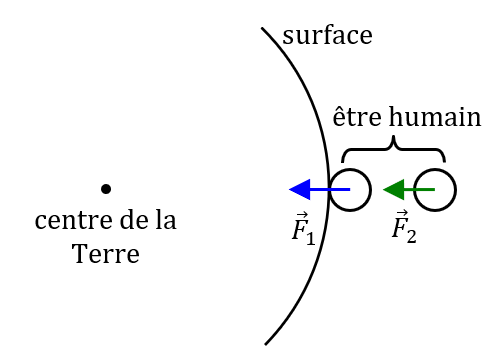
$*F_1 = {GM_Tm \over R_T^2}*$ = 344,11513 N et $*F_2 = {GM_Tm \over (R_T+1)^2}*$ = 344,11503 N
$*F_1 - F_2*$ = 1,0·10-4 N
Remarque : il faut beaucoup de chiffres significatifs pour constater la différence entre les deux forces.
Conclusion : la différence entre ces deux forces est infime.
2. Le schéma est le même, mais il faut remplacer $*M_T*$ par la masse du trou noir et $*R_T*$ par 1000 km (soit 106 m). On trouve cette fois $*F_1 – F_2*$ = 6,5·104 N.
Cette différence de force correspond au poids d’un objet d’environ 6,5 t à la surface de la Terre (un petit camion). Conclusion : l’être humain sera écartelé par cette différence de force.
Champ gravitationnel de Mars
Cet exercice a été donné en devoir en 2020/2021
Mars est une planète rocheuse plus petite que la Terre. Des projets plus ou moins réalistes de colonisation de la planète Mars existent depuis plus de 50 ans.
L’objectif de cet exercice est d’évaluer l’intensité de son champ de pesanteur.
Données
- Masse de Mars : $*M*$ = 6,42·1023 kg
- Rayon moyen de Mars : $*R*$ = 3400 km
- Masse volumique de Mars : $* \rho *$ = 3,9·103 kg·m-3
- Constante de gravitation universelle : $*G*$ = 6,67·10-11 S.I.
- Volume d’une sphère de rayon $*r*$ : $* V = \dfrac 43 \pi r^3*$
1 En vous servant des données, montrer que la masse de Mars est de 6,42·1023 kg.
2.a. Donner l’expression du poids d’un objet de masse $*m*$ situé à une altitude $*z*$ de la surface de Mars. On assimilera le poids à la force d’attraction gravitationnelle.
2.b. Calculer ce poids pour un objet de 1 kg à la surface de Mars. En déduire l’intensité de pesanteur $*g_M*$ de Mars à sa surface.
Correction
1. $*m = ρV = 3,9·10^3 × \dfrac 43 × \pi ×(3,4·10^6)^3 = 6,42·10^{23}*$ kg
2.a. Force gravitationnelle exercée par Mars $µ F = \frac {GMm}{(R_M+z)^2} µ$
2.b. $* F = \dfrac {6,67·10^{-11}×6,42·10^{23}×1}{(3400·10^3 )^2} = 3,7*$ N
L’intensité de la pesanteur est donc de 3,7 N·kg-1.