Physique & Chimie au lycée

Cours de physique-chimie pour les classes de 1ère et Terminale

Sommaire
SP-1 ES-1
SP-T ES-T
3e SNT
Divers Annales
Contact

P2. Mouvement

Dans ce chapitre, nous allons reparler de la notion de mouvement, qui a, normalement, largement été traitée dans les classes précédentes. J’irai donc un peu vite, mais je reprendrai tout de même tout à zéro.

Référentiel et trajectoire
  • Caractériser le mouvement d’un objet.
  • Relativité du mouvement dans des cas simples.
  • Mouvements rectilignes et circulaires.

Un mouvement, en physique, c’est le déplacement d’un objet par rapport à un autre, nommé référentiel. On caractérise (c’est-à-dire qu’on décrit) le mouvement d’un objet par sa trajectoire et l’évolution de sa vitesse.
Nous reviendrons sur ces deux termes un peu plus loin.

Mouvement d’un ballon lancé dans un panier

Référentiel

Il n’existe pas de mouvement « absolu ». Le mouvement d’un objet est toujours décrit par rapport à quelque chose, que l’on appelle un référentiel.

Le plus souvent dans la vie quotidienne, ce référentiel, c’est le sol, aussi appelé référentiel terrestre. On choisit ce référentiel sans même y penser. Mais en physique, il faudra toujours expliciter le référentiel par rapport auquel on étudie le mouvement d’un objet.

Relativité du mouvement
Animation n°1
Animation n°2

Un exemple simple pour fixer les idées. Imaginez une voiture sur le plateau d’un camion. Ce camion se déplace sur la route.

La voiture est-elle immobile ?

Vous voyez bien qu’il n’y a pas une réponse unique à cette question. On peut tout aussi bien répondre :

  • « Non, la voiture n’est pas immobile, car elle est sur le camion qui se déplace ».
  • « Oui, la voiture est immobile, car elle ne bouge pas sur le camion ».

C’est la question qui est mal posée… 😊 Il aurait fallu préciser par rapport à quel référentiel on pose la question. La voiture n’est pas immobile dans le référentiel terrestre. Mais elle est immobile par rapport au camion.

Relativité du mouvement

1. Donner un autre exemple de situation où un objet est en mouvement dans un référentiel donné et immobile dans un autre référentiel.

2. Lorsqu’on dit que l’orbite de la Terre est un cercle, quel est le référentiel qui est sous-entendu ?

Trajectoire

La trajectoire d’un objet (ou d’un point d’un objet) est l’ensemble des positions qu’a ce point au cours de son mouvement.

Animation sur les trajectoires

Lorsqu’un objet se déplace en ligne droite, ses positions successives au cours du temps forment une droite. On dit que la trajectoire est rectiligne. Lorsque vous lâchez un objet sans vitesse initiale, cet objet aura alors une trajectoire rectiligne jusqu’à ce qu’il rencontre un obstacle.

Lorsqu’un objet en mouvement décrit un cercle, ses positions successives forment un cercle (ou un arc de cercle). On dit que son mouvement est circulaire. C’est le cas de la Terre dans son mouvement par rapport au Soleil.

Bien sûr, il n’y a pas que ces trajectoires qui existent… Pensez au mouvement d’une fourmi. Sa trajectoire est très complexe et ne ressemble à aucune forme mathématique simple.

Parmi les trajectoires simples qui se rencontrent facilement dans la vie quotidienne, il y a celle d’un objet lancé. Même si elle n’est pas au programme, je vous en parle brièvement. Lorsque vous jetez une pierre ou un ballon autrement que verticalement, la trajectoire qu’il va suivre a la forme d’une courbe qui, en mathématiques, s’appelle une « parabole ».
On dit que sa trajectoire est parabolique.

Trajectoire

Donner un exemple de trajectoire rectiligne et un exemple de trajectoire circulaire tirés de la vie quotidienne et qui soient différents de ceux abordés dans le cours.

Vitesse
  • Vitesse : direction, sens et valeur.
  • Utiliser la relation liant vitesse, distance et durée dans le cas d’un mouvement uniforme.
  • Mouvements uniformes et mouvements dont la vitesse varie au cours du temps en direction ou en valeur.

Vecteur vitesse

Pour décrire la vitesse d’un objet, indiquer sa valeur ne suffit pas. Dire qu’un avion se déplace à 900 km·h-1 ne nous dit pas dans quelle direction il se déplace. Pour décrire une vitesse, il faut aussi indique sa direction.

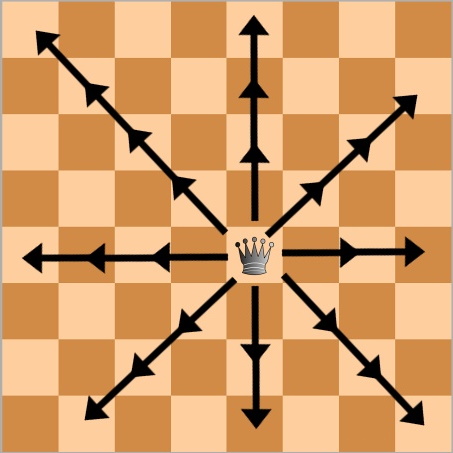
Au échec, la reine peut se déplacer selon les directions indiquées, d’autant de case que l’on souhaite.

Si vous jouez aux échecs contre un ordinateur et que vous souhaitez déplacer votre reine, vous ne pouvez pas indiquer à l’ordinateur « je déplace ma reine de trois cases ». Il faut également lui dire dans quelle direction vous souhaitez la déplacer. Il faut donc indiquer un vecteur déplacement et non pas juste une valeur de déplacement.

En mathématique, un « outil » permettant de décrire à la fois une valeur et une direction (en fait, une valeur, un sens et une direction) est un vecteur.

  • La valeur d’un vecteur est sa norme (sa longueur)
  • La direction d’un vecteur est une droite parallèle au vecteur
  • Le sens du vecteur indique de quelle côté de la droite le vecteur pointe.

Décollage d’un drone

Un drone décolle du sol avec une vitesse de 1 m·s-1. La direction de sa vitesse est une droite faisant un angle de 45° avec l’horizontale. Le sens de la vitesse est vers le haut (évidemment, puisqu’il décolle).

1. Faites un schéma représentant le sol par une droite horizontale. Placez-y la position initiale du drone. Puis tracez la droite représentant la trajectoire du drone.

2. À quelle altitude se trouve le drone après 3 secondes d’ascension ?

3. Quelle serait son altitude si le drone avait décollé verticalement, avec la même valeur de vitesse ?

Vitesse, distance et temps

La vitesse moyenne $*v*$ d’un objet peut se calculer si on connaît la distance $*d*$ qu’il a parcouru pendant une durée $*\Delta t*$

$µ v = \frac d {\Delta t} µ$

La vitesse calculée de cette manière est une vitesse moyenne. Ce n’est pas forcément la vitesse de l’objet à un instant donné, sauf si l’objet a une vitesse constante.

Un randonneur marche pendant 1 h et parcourt 4,5 km. Puis il fait une pause de 15 minutes. Il reprend sa route et parcourt 2 kilomètre en 30 minutes.
Son temps de marche est donc de 1 + 0,25 + 0,5 = 1,75 h. La distance parcourue est de 6,5 km. Sa vitesse moyenne est de $*v*$ = 6,5÷1,75 = 3,7 km·h-1. Mais cette vitesse tient compte de son arrêt de 15 minutes. Elle ne correspond donc pas à la vitesse à laquelle se déplace le randonneur.

Unité de la vitesse

Dans le système international d’unités (appelée système S.I.), une vitesse doit être exprimée en m·s-1. Mais ce n’est pas toujours nécessaire. Si la distance est exprimée en km et la durée en heure, vous obtiendrez des km·h-1.

Rappel : 1 m·s-1 = 3,6 km·h-1

Vitesse

1. La distance entre Belgrade et Paris est de 1700 km. Pour parcourir cette distance, un avion met 2h30. Calculer sa vitesse moyenne en km·h-1 et en m·s-1.

2. Quelle sera la durée d’un vol Belgrade – Bâle, distantes de 1300 km, à la même vitesse ?

Variation de la vitesse

Lorsque la valeur de la vitesse d’un objet ne varie pas au cours de son mouvement, on dit que son mouvement est uniforme.

  • Un objet qui se déplace en ligne droite avec une valeur de vitesse constante a un mouvement rectiligne uniforme.
  • Un objet qui parcourt un cercle avec une valeur de vitesse constante a un mouvement circulaire uniforme.

Variation de la valeur de la vitesse

Prenons l’exemple d’une voiture se déplaçant sur une route. À l’approche d’un virage, le conducteur freine. La valeur de la vitesse de la voiture diminue. Puis en sortie de virage, le conducteur accélère. La valeur de la vitesse augmente.

Ainsi, la valeur de la vitesse varie lorsqu’un objet ralentit ou accélère.

Variation de la direction et du sens de la vitesse

Mais n’oubliez pas que la vitesse est un vecteur ! Sa valeur peut varier, mais aussi sa direction et son sens. Ainsi, lorsque la voiture prend un virage, la direction de la vitesse varie tout on long de la courbe du virage. Donc le vecteur vitesse varie, même si le conducteur prend le virage avec une valeur de la vitesse constante.

Dans un mouvement circulaire uniforme, la valeur de la vitesse est constante, mais la direction du vecteur vitesse change en permanence.

Voici trois situations particulières, où on a appelé $*\vec{a}*$ la variation du vecteur vitesse $*\vec{v}*$.

Situation Signification
$*\vec{v}*$ et $*\vec{a}*$ ont même sens et même direction : l’objet se déplace en ligne droite à une vitesse croissante.
$*\vec{v}*$ et $*\vec{a}*$ ont la même direction mais un sens opposé : l’objet se déplace en ligne droite à une vitesse décroissante.
$*\vec{v}*$ et $*\vec{a}*$ sont orthogonaux : l’objet tourne dans le sens indiqué par $*\vec{a}*$ à vitesse constante

Variation du vecteur vitesse

1. Donner un exemple de mouvement pour lequel le vecteur vitesse de l’objet en mouvement ne varie pas en valeur, mais seulement en direction.

2. Donner un exemple de mouvement pour lequel le vecteur vitesse de l’objet en mouvement ne varie pas en direction, mais seulement en valeur.

TP Étude d’un mouvement

Dans ce TP, nous allons étudier le mouvement d’un ballon de basket lancé dans un panier. Pour cela, nous allons exploiter cette vidéo.

Pointage du mouvement du ballon

  • Télécharger la vidéo sur le bureau
  • Réaliser le pointage du mouvement du ballon avec le logiciel Regressi en suivant le tuto que je vous ai fait. Le pointage ne se fait que lorsque la joueuse ne touche plus le ballon et que celui-ci ne touche pas le panier.
  • Copier les valeurs obtenues dans Excel.

Affichage de la trajectoire

  • Sur Excel, affiche le graphique montrant la trajectoire $*y(x)*$ du ballon.
Questions

1. Quel intervalle de temps sépare chaque position du ballon ?

2. Que peut-on dire de la vitesse du ballon au cours de son mouvement, simplement en observant ce graphique ?

Vitesse du ballon

  • À l’aide d’Excel, calculer la valeur de la vitesse du ballon sur les différentes parties de sa trajectoire.
Question

Quels sont la direction et le sens du vecteur vitesse du ballon entre deux positions successives ?