P2. Mouvement dans un champ uniforme
On va s’intéresser, dans ce (très long) chapitre, au mouvement d’un objet lorsqu’il est placé dans un champ gravitationnel ou électrique uniforme (c’est-à-dire identique en tous points de l’espace).
Deuxième loi de Newton
- Justifier qualitativement la position du centre de masse d’un système, cette position étant donnée.
- Discuter qualitativement du caractère galiléen d’un référentiel donné pour le mouvement étudié.
- Utiliser la deuxième loi de Newton dans des situations variées pour en déduire :
- le vecteur accélération du centre de masse, les forces appliquées au système étant connues ;
- la somme des forces appliquées au système, le mouvement du centre de masse étant connu.
La deuxième loi de Newton, appelée aussi la relation fondamentale de la dynamique (abrégée RFD) a été le pilier de la mécanique jusqu’à la mise au point de la Relativité d’Einstein et de la mécanique quantique, au début du XXe siècle. Elle est encore très utilisée aujourd’hui car dans la plupart des situations courantes en physique, les effets relativistes ou quantiques ne se manifestent pas.

On l’a vue l’année dernière, souvenez-vous… Voilà ce que je vous disais :
La somme vectorielle des forces appliquées sur un objet de masse $*m*$ lui communique une accélération $*\vec{a}*$ vérifiant la relation : $µ \sum \vec{F}_{ext} = m\vec{a} µ$
Cette relation est dite « approchée » si on utilise le vecteur accélération moyenne (…) Pour utiliser rigoureusement cette relation, il faut faire appel à des notions mathématiques (dérivée et primitive de fonctions) qui ne sont pas au programme de SPC cette année mais qui seront utilisées l’année prochaine.
Eh bien l’année prochaine, c’est maintenant ! 😊
Mais d’abord, il y a une petite chose à clarifier. Dans toute la mécanique du lycée, on réduira les objets à un simple point qui concentre toute la masse de cet objet – je vous le disais dans le chapitre précédent. Ce point n’est pas n’importe quel point : il s’agit du centre de masse (ou centre de gravité) de l’objet
Centre de masse d’un objet
Le centre de masse d’un objet, qu’on appelle aussi son centre de gravité, c’est un point qui correspond à la « position moyenne » de sa masse.
C’est important que vous compreniez à quoi il correspond, car, comme je vous le disais dans le chapitre précédent, on ne va étudier des mouvements d’objets uniquement en les réduisant à un point, qui correspond à leur centre de masse.
Concrètement, ça correspond à quoi, le centre de masse ? Eh bien, mathématiquement, imaginez qu’on divise l’objet en un très très grand nombre de morceaux très très petits (pour fixer les idées, on va dire que chaque morceau correspond à un atome) que l’on va noter Mi. Chaque morceau a une masse très très petite (la masse d’un atome) qu’on va noter $*\delta m*$.
Le centre de gravité est tel que : $µ \sum_i \delta m · \overrightarrow{GM}_i = \vec{0} µ$
Oui, c’est comme ça qu’est défini mathématiquement le centre de masse d’un objet. Bonne nouvelle : inutile de retenir ce truc. On va maintenant s’intéresser aux propriétés physiques du centre de masse. C’est plus simple à comprendre.
Il a deux propriétés intéressantes :
- Si l’objet peut tourner librement sur lui-même (par exemple, si vous le lancez en l’air en le faisant tournoyer), il va tourner autour de son centre de gravité.
- Si le centre de gravité ne se trouve pas au-dessus de sa surface de contact avec le sol… il bascule. Regardez le schéma ci-dessous pour mieux comprendre.
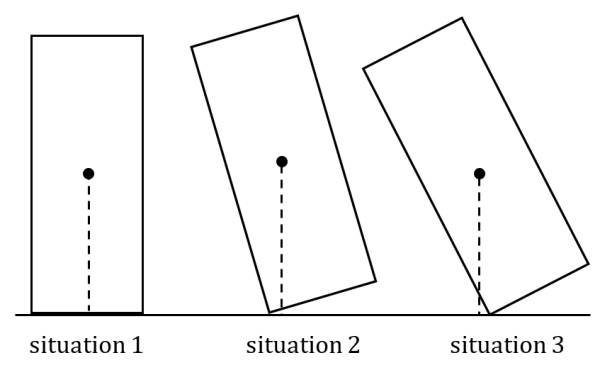
Dans la situation 1, le centre de gravité de l’objet, matérialisé par un point noir, se trouve au-dessus de la surface de contact. L’objet est en équilibre stable.
Dans la situation 2, son centre de gravité n’est pas au-dessus de la surface de contact, qui est très réduite car l’objet repose sur un coin. Il va donc basculer vers la droite.
Dans la situation 3, l’objet bascule vers la gauche.
À propos de la 2e loi de Newton
Nous voilà dans le point central de ce paragraphe. Donc, comme je vous le disais plus haut, la deuxième loi de Newton, aussi appelée RFD, s’écrit :
La première loi est appelé le principe d’inertie. Vous la connaissez depuis la seconde :
$* \sum \vec{F}_{ext} = \vec{0} \Leftrightarrow *$ système immobile ou en mouvement rectiligne uniforme (MRU).
Cette première loi, vous pouvez l’oublier, car elle est en fait une conséquence de la deuxième loi. Si vous connaissez la deuxième loi, alors vous connaissez la première.
Elle mérite quelques petites explications.
Force extérieure
Le terme $* \sum \vec{F}_{ext} *$ se lit : « somme des forces extérieures ». Mais qu’est-ce qu’une « force extérieure » ? Et extérieure à quoi, d’abord ?
Eh bien rappelez-vous, on étudie le mouvement d’un système qui doit être parfaitement défini au préalable. Si on étudie le lancé d’un ballon, les forces extérieures au ballon sont celles exercées par la main du lanceur (tant qu’il y a un contact), le poids du ballon et les frottements dans l’air. Ce sont elles qui vont avoir une influence sur l’accélération du ballon et donc sur son mouvement.
La force exercée par l’air sous pression à l’intérieur du ballon n’est pas une force extérieure. Elle n’a aucun rôle sur le mouvement du ballon (du moins tant qu’il ne rebondit pas, mais là il se passe d’autres trucs dont je ne veux pas parler ici.
Donc quand on dit « forces extérieures », on sous-entend « forces extérieures au système ».
Somme des forces extérieures
Remarquez bien qu’on parle de la somme des forces extérieures. Il s’agit de la somme de vecteurs. C’est donc un vecteur, éventuellement égal au vecteur nul $*\vec{0}*$. Cette somme est parfois aussi appelée la résultante des forces (extérieures). Tout se passe comme si il n’y avait qu’une seule force égale à la somme vectorielle des forces extérieures (ou pas de force du tout si la résultante est nulle).
Masse × vecteur accélération
$*m\vec{a}*$ est le produit de la masse $*m*$ du système par le vecteur accélération $*\vec{a}*$.
Qu’est-ce qu’on fait avec ça ?
Eh bien grâce à cette loi, si on connaît les forces qui s’appliquent à notre système et qu’on connaît sa position et sa vitesse initiale, alors on peut entièrement prévoir son mouvement ! 😎
C’est ce qu’on va faire dans le reste du chapitre.
Référentiel galiléen
Une avant-dernière petite chose avant de commencer à utiliser la RFD pour prévoir des mouvements. La RFD ne s’applique que dans des référentiels galiléens. Qu’est-ce qu’un référentiel galiléen ? C’est un référentiel dans lequel la RFD peut s’appliquer. 😊
Oui ! On tourne en rond. 🔄
Je vais vous donner un exemple pour mieux vous faire sentir les choses et vous faire comprendre pourquoi la définition d’un référentiel galiléen tourne en rond. Imaginez une balle posée sur une surface parfaitement horizontale, dans une voiture. La balle est initialement immobile, donc d’après le principe d’inertie ($* \sum \vec{F}_{ext} = \vec{0} \Leftrightarrow *$ système immobile ou en MRU), la résultante des forces qui s’appliquent sur elle (son poids et la réaction du support) est nulle. Si la voiture se met à accélérer (dans le sens commun du terme), la balle va se mettre en mouvement vers l’arrière de la voiture. Et pourtant aucune nouvelle force n’est apparue sur la balle. Cette mise en mouvement est uniquement due à l’accélération de la voiture. On a ici un exemple de situation où la RFD ne s’applique pas. Le référentiel de la voiture est non galiléen.
C’est une question simple à laquelle il est compliqué de répondre… 😊 En fait, un référentiel galiléen, ça n’existe pas dans l’absolu. Prenons par exemple le référentiel terrestre. Est-il galiléen ?
La réponse est oui… et non. Ça dépend du mouvement que l’on étudie.
Si on étudie un mouvement relativement localisé, le référentiel terrestre peut être considéré comme galiléen. Mais on si considère un mouvement qui se déroule dans un espace plus grand, on peut observer l’effet de la rotation de la Terre sur elle-même. Par exemple, Ferdinand Reich, en 1831, fit tomber des projectiles dans un puits de 158 m de profondeur à Freiberg (Saxe). Il observa une déviation des projectiles de 28 mm vers l’est au cours de leur chute. Le caractère non galiléen du référentiel terrestre est mis en évidence par cette expérience.
Ce qu’il faut retenir
- La RFD (et le principe d’inertie) ne se vérifient que dans un référentiel galiléen.
- Le référentiel terrestre peut être considéré comme galiléen pour des mouvements localisés.
- Un référentiel en MRU par rapport à un référentiel galiléen est lui aussi galiléen.
- Un référentiel dont le vecteur accélération n’est pas nul par rapport à un référence galiléen n’est pas galiléen.
Faire un bilan des forces
Allez, encore une dernière chose, très importante…
Vous l’aurez compris, si on connaît toutes les forces qui s’appliquent sur un objet, on peut en déduire son vecteur accélération $*\vec{a}*$ et ensuite, par intégration, comme on l’a vu au chapitre P1, on peut connaître sa vitesse et sa position.
Faire un bilan des forces, c’est dénombrer toutes les forces qui s’appliquent à un système, en connaissant leurs caractéristiques (intensité et direction/sens). Si ce bilan est mal fait, tout ce que vous calculerez ensuite sera faux, donc il ne faut pas se louper à ce stade.
Facile ! Il n’y a que deux types de forces qui peuvent s’exercer à distance : l’interaction gravitationnelle et l’interaction électromagnétique. Donc si votre système se trouve dans un champ gravitationnel, il sera soumis à son poids. Et s’il est chargé électriquement et qu’il se trouve dans un champ électrique, il sera soumis à une force électrique (on ne traitera jamais le cas du magnétisme, plus complexe).
Toutes les autres forces s’exercent par contact. Donc faites l’inventaire de ce qui est en contact avec le système (n’oubliez pas l’air lui-même).
Liste des forces les plus courantes
- Le poids $*\vec{P}*$ : vertical vers le bas. $*P = mg*$.
- La force électrique $*\vec{F}_e*$ : $*\vec{F}_e = q\vec{E}*$.
- La réaction du support $*\vec{R}*$ : si l’objet est posé sur un support, cette force est perpendiculaire au support. $*R*$ et $*P*$ ont même valeur si le support est horizontal. Si ce n’est pas le cas, c’est plus compliqué. On verra ça dans un exercice un peu plus loin.
- Les frottements $*\vec{f}*$ : leur direction est celui du vecteur vitesse s’il y a déplacement. Si l’objet est immobile (par exemple sur un plan légèrement incliné, les frottements empêchant l’objet de glisser), leur direction est la même que celui qu’aurait le mouvement de l’objet s’il pouvait glisser. Le sens est toujours opposé au mouvement. La valeur des frottements est une question complexe car elle varie selon la vitesse de l’objet. En général, on les néglige, sinon l’étude mathématique du mouvement se corse beaucoup, mais on en reparlera.
- La poussé d’Archimède $*\vec{\Pi}_A*$ : tout corps plongé dans un fluide (un liquide ou un gaz) subit une poussée verticale égale ou poids du volume de fluide déplacé. La plupart du temps, dans l’air, cette poussée est négligeable… sauf si on étudie un ballon gonflé à l’hélium, par exemple. Dans l’eau, c’est une autre histoire.
Ne vous inquiétez pas, il est inutile de connaître toutes ces forces par cœur. Vous serez toujours placés, en examen et en contrôle, dans une situation où on peut négliger toutes les forces sauf une (le poids ou la force électrique).
Allez, trève de théorie. Il est l’heure de mettre un peu en pratique. Les deux exercices qui suivent vont vous permettre de rencontrer au moins une fois tous les problèmes que vous devez savoir traiter.
Décollage du rafale
Le Rafale est un avion de chasse français. Sa masse, armé et avec le plein de carburant, est de 23,7 t. Il dispose de deux turboréacteurs d’une poussée unitaire de 50 kN. Sa vitesse de décollage est de 213 km·h-1.
Le porte-avion Charles de Gaulle comporte une piste de 195 m.

Problème : le Rafale est-il capable de décoller du Charles de Gaulle sans catapulte ? On négligera les frottements.
Remarque : une catapulte sert à communiquer à l’avion un complément d’accélération en plus de celle fournie par ses turboréacteurs.
Un peu de méthode
- Définissez le sytème que vous étudiez (ici l’avion), le référentiel de l’étude et le repère le plus simple possible.
- Faites le bilan des forces et donner les coordonnées de la résultante des forces extérieures dans votre repère.
- Vous obtenez ainsi le vecteur accélération $*\vec{a}*$ par application de la RFD.
- Intégrez une première fois $*\vec{a}*$ pour obtenir les coordonnées de $*\vec{v}*$. Pensez bien aux constantes d’intégration que vous pouvez calculer en connaissant $*\vec{v}_0*$.
- Faites encore une fois la même chose avec $*\vec{v}*$ pour obtenir les coordonnées du vecteur position.
- Enfin, traduisez en équation la problématique posée. Ici, c’est : est-ce que l’avion atteint une vitesse de 213 km·h-1 après avoir parcouru 195 m ?
Si vous bloquez dès le départ, voyez l’aide n°1 ci-dessous. Pressez-vous un peu le 🍋, mais si vous n’y arrivez pas, ce n’est pas grave, c’est la première fois. 😊
Aide n°1
Pour le système, c’est facile, c’est l’avion. Pour le référentiel, c’est… le vent. Mais comme on ne nous dit rien sur le vent, on va supposer qu’il n’y en a pas et on va prendre comme référentiel le porte-avions. Ensuite, choisissez correctement votre repère : un axe vertical orienté vers le haut (disons $*\mathrm{O}y*$) et un axe horizontal ($*\mathrm{O}x*$) orienté dans le sens du mouvement de l’avion. L’origine O du repère coïncide avec l’avion – assimilé à un point – juste avant qu’il ne se lance. Faites un schéma. C’est très important en physique. J’en ai mis un dans l’aide n°2.
Faites un bilan des forces. Au moment où l’avion allume ses réacteurs, il y en a 3. Deux verticales et une horizontale. Trouvez-les et donnez les coordonnées des vecteurs qui les modélisent dans notre repère. Justifiez du fait que les deux forces horizontales se compensent.
Si vous bloquez sur le bilan des forces, voyez l’aide n°2 ci-dessous. 😏
Aide n°2
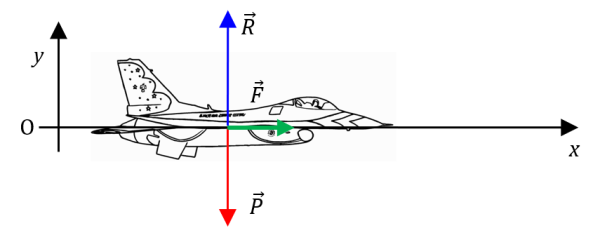
Les trois forces sont : le poids, d’intensité $*P = mg*$, la réaction de la piste, qui a la même intensité que le poids car l’avion se déplace à l’horizontal, donc son accélération verticale est nulle et donc la somme des composantes verticales des forces doit être nulle aussi ! Enfin il y a la poussée des réacteurs, d’intensité $*F*$ = 2×50 kN, de direction horizontale et orientée vers l’avant de l’avion. Voici les coordonnées de ces forces :
$µ \vec{P} \begin{pmatrix} \begin{aligned} P_x &= 0 \\ P_y &= -mg \\ \end{aligned} \end{pmatrix} \quad \vec{R} \begin{pmatrix} \begin{aligned} R_x &= 0 \\ R_y &= mg \\ \end{aligned} \end{pmatrix} \quad \vec{F} \begin{pmatrix} \begin{aligned} F_x &= F \\ F_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
Et les frottements dans tout ça ? Eh bien on ne va pas en tenir compte. Ils ne sont pas très importants comparés à la poussée des réacteurs. Et de toute façon, sauf cas très particuliers (on verra ça dans l’exercice suivant) vous ne pouvez pas tenir compte des frottements parce que d’une part il manque des données dans l’exercice, et d’autre part ça serait trop compliqué mathématiquement.
Si vous bloquez pour trouver les coordonnées du vecteur accélération, voyez l’aide n°3 ci-dessous. 😑
Aide n°3
Il suffit maintenant d’ajouter ces trois forces :
$µ \sum \vec{F}_{ext} \begin{pmatrix} \begin{aligned} P_x + R_x + F_x &= F \\ P_y + R_y + F_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
On a maintenant les coordonnées de $*\vec{a}*$ grâce à la RFD :
$µ \vec{a} \begin{pmatrix} \begin{aligned} a_x &= \frac Fm \\ a_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
Si vous bloquez pour trouver les coordonnées vitesse et position, voyez l’aide n°4 ci-dessous. Mais là, c’est déjà moins pardonnable… 😒
Aide n°4
On sait que l’avion est immobile à $*t*$ = 0. Donc $*v_{0x}*$ = $*v_{0y}*$ = 0.
On a choisi l’origine du repère à la position initiale de l’avion. Donc $*x_0*$ = $*y_0*$ = 0.
Vous devez vous débrouiller avec ça pour trouver :
$µ \vec{v} \begin{pmatrix} \begin{aligned} v_x &= \frac Fm t \\ v_y &= 0 \\ \end{aligned} \end{pmatrix} \quad \overrightarrow{OM} \begin{pmatrix} \begin{aligned} x &= \frac 12 \frac Fm t^2 \\ y &= 0 \\ \end{aligned} \end{pmatrix} µ$
Correction
Une partie de la correction ayant été fournie sous forme d’aides, je ne mets là que la partie finale de l’exercice.
Répondre à la question posée, c’est savoir si, après 195 m de parcours, l’avion a bien atteint la vitesse de 213 km·h-1 (soit 59,2 m·s-1). Pour cela, on peut calculer le temps au bout duquel l’avion a parcouru les 195 m de la piste ($*x_f*$ = 195 m), que l’on note $*t_f*$, par exemple, et calculer la valeur de la vitesse pour cette date :
$µ \begin{aligned} t_f &= \sqrt{ 2mx_f \over F } \\ t_f &= \sqrt{ 2×23,7·10^3×195 \over 2×50·10^3 } \\ t_f &= 9,61 \; \mathrm{s} \end{aligned} µ$
Puis :
$µ \begin{aligned} v_f &= \frac Fm t_f \\ v_f &= { 2×50·10^3 \over 23,7·10^3}×9,61 \\ v_f &= 40,6 \; \mathrm{m·s^{-1}} \end{aligned} µ$
On voit que la vitesse est inférieure à la vitesse requise (59,2 m·s-1). Donc la réponse à la question est non.
Une autre stratégie est possible : calculer le temps (on dit aussi la date) au bout duquel la vitesse de 59,2 m·s-1 est atteinte, puis calculer la distance parcourue par l’avion à cette date. On trouve que la vitesse voulue est atteinte au bout de 14,0 s ce qui correspond à une distance parcourue du 415 m. Les deux manières de faire sont tout à fait valables.
Luge
Un enfant sur sa luge descend une pente faisant un angle $*\alpha*$ de 10° avec l’horizontale. Après un certain temps, il atteint une vitesse constante à cause des frottements. Cette vitesse vaut $*v_f*$ = 10 m·s-1. L’ensemble {luge + enfant} pèse $*m*$ = 40 kg.
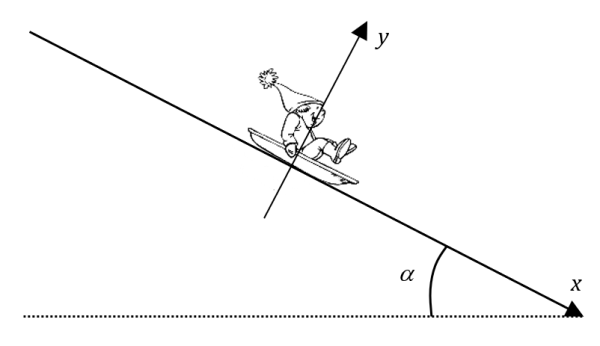
Je vous suggère le repère suivant pour le maximum de simplicité : un axe $*\mathrm{O}x*$ parallèle à la piste orienté dans le sens du mouvement de la luge, et un axe $*\mathrm{O}y*$ orienté vers le haut, perpendiculaire à la piste.
Problème : quelle est la valeur de la force créée par les frottements ?
Correction
Il faut d’abord faire un bilan des forces qui s’excercent sur la luge, sur un schéma. Il faut toujours faire un schéma ! 🤓
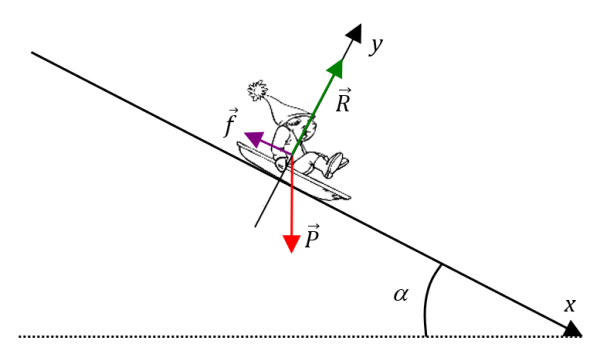
$µ \vec{P} \begin{pmatrix} \begin{aligned} P_x &= mg\sin \alpha \\ P_y &= -mg\cos \alpha \\ \end{aligned} \end{pmatrix} \quad \vec{R} \begin{pmatrix} \begin{aligned} R_x &= 0 \\ R_y &= R \\ \end{aligned} \end{pmatrix} \quad \vec{F} \begin{pmatrix} \begin{aligned} f_x &= -f \\ f_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
L’énoncé dit que la luge a une vitesse constante et comme la luge se déplace en ligne droite (l’énoncé ne dit rien là-dessus, mais si ça n’avait pas été le cas, l’énoncé l’aurait mentionné…), alors $*\vec{v}*$ est constant et donc $*\vec{a} = \vec{0}*$. D’après la RFD, cela implique que la somme vectorielle des forces est nulle. Donc :
$µ \sum \vec{F}_{ext} \begin{pmatrix} \begin{aligned} P_x + R_x + f_x &= 0 \\ P_y + R_y + f_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
Soit :
$µ \sum \vec{F}_{ext} \begin{pmatrix} \begin{aligned} mg\sin \alpha + 0 - f &= 0 \\ -mg\cos \alpha + R + 0 &= 0 \\ \end{aligned} \end{pmatrix} µ$
Donc $*f = mg\sin \alpha \simeq*$ 70 N
Remarquez au passage que $*R*$ ici ne vaut pas $*P*$ car le support est incliné. $*R = mg\cos \alpha*$. Si le plan n’est pas incliné, $*\alpha*$ vaut 0 et donc $*\cos \alpha*$ vaut 1 et on retrouve bien que $*R = mg = P*$. 😊
Méthode de résolution d’un exercice de mécanique
- Définir sytème, référentiel et repère.
- Bilan des forces → coordonnées de $*\Sigma \vec{F}_{ext}*$
- Coordonnées de $*\vec{a}*$ grâce à la RFD.
- Intégrer $*\vec{a}*$ pour avoir $*\vec{v}*$
- Intégrer $*\vec{v}*$ pour avoir le vecteur position $*\overrightarrow{OM}*$
- Traduire en équation la problématique posée.
✋ Apprenez par cœur cette suite d’étapes !
Mouvement dans un champ uniforme
- Montrer que le mouvement dans un champ uniforme est plan.
- Établir et exploiter les équations horaires du mouvement.
- Établir l’équation de la trajectoire.
Nous avons déjà vu toute la théorie nécessaire pour prévoir le mouvement d’un objet soumis à une force constante.
Vous serez confronté à deux situations possibles :
- un objet de masse $*m*$ placé dans un champ gravitationnel uniforme $*\vec{g}*$.
- une particule possédant une charge $*q*$ dans un champ électrique uniforme $*\vec{E}*$.
Ces deux situations sont en fait très similaires. Le traitement mathématique de la situation est le même dans les deux cas car le système étudié est soumis à une force unique ($*\vec{P}=m\vec{g}*$ ou $*\vec{F}_e=q\vec{E}*$).
C’est vrai ! Mais lorsqu’on étudie le mouvement d’un électron ou d’un proton dans un champ électrique, son poids a une influence complètement négligeable.
Et quand bien même ça ne serait pas le cas (imaginons le mouvement d’un proton dans un champ électrique extrêmement faible, de telle sorte que le poids du proton ne soit pas négligeable devant la force électrique qu’il subit (dans la pratique, ça serait très difficile à réaliser…), la résultante de deux forces constantes, c’est aussi un vecteur constant. Donc ça ne change rien non plus… 😊
Planéité du mouvement
Le mouvement d’un système dans un champ uniforme est forcément plan. Le système reste, tout au long de son mouvement, dans un plan défini par la force due au champ (poids ou force électrique) et le vecteur vitesse initiale.
Vous devez savoir démontrer que le mouvement d’une particule dans un champ uniforme est plan et donc comprendre et savoir refaire la démonstration suivante.
Démonstration
Prenons la situation la plus générale possible. Considérons un système ponctuel soumis à une force constante $*\vec{F}*$ et qui possède une vitesse initiale $*\vec{v}_0*$. Ces deux vecteurs définissent un plan, que je vais appeler $*\mathcal{P}*$ pour me simplifier la vie dans la suite de mes explications.
On définit maintenant un repère qui a deux de ses axes dans ce plan (disons les axes $*\mathrm{O}x*$ et $*\mathrm{O}y*$), et un troisième axe $*\mathrm{O}z*$ perpendiculaire à ce plan.
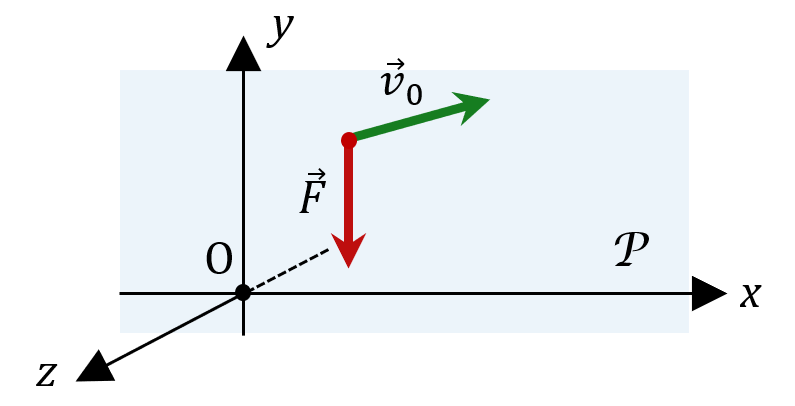
Donc la coordonnée $*v_z*$ du vecteur vitesse est constante.
Mais, rappelez-vous, on a aussi défini $*\mathcal{P}*$ de telle sorte que le vecteur vitesse $*\vec{v}_0*$ soit dans ce plan. Ça veut aussi dire que $*v_{0z}*$ = 0.
Du coup, on a la coordonnée $*v_z*$ du vecteur vitesse qui, initialement, est nulle, et qui en plus ne varie jamais. Donc le vecteur vitesse est toujours dans le plan $*\mathcal{P}*$.
Et comme le vecteur vitesse est tangent à la trajectoire du système, alors ça implique forcément que la trajectoire reste toujours dans le plan $*\mathcal{P}*$. CQFD.
La même démo en langage de matheux
- Soit un point matériel soumis à une force constante $*\vec{F}*$ et possèdant une vitesse initiale $*\vec{v}_0*$.
- Soit $*\mathcal{P}*$ le plan défini par $*\vec{F}*$ et $*\vec{v}_0*$
- Soit $*\mathcal{R}*$ un repère orthogonal d’axes $*\mathrm{O}x*$ et $*\mathrm{O}y*$ dans $*\mathcal{P}*$ et d’axe $*\mathrm{O}z*$ perpendiculaire à $*\mathcal{P}*$. L’origine de $*\mathcal{R}*$ se trouve dans $*\mathcal{P}*$.
- $*F_z = 0 \Rightarrow a_z = 0 \Rightarrow v_z = cste*$
- Or $*v_{0z} = 0*$
- Donc $*v_z = 0 \; \forall \; t*$
- Donc $*z*$ = cste = $*z_0*$ = 0. CQFD.
Équations du mouvement
Et comme vous savez déjà tout, c’est vous qui allez rédiger le cours grâce à un exercice. 😄
Mouvement dans un champ uniforme
Le repère utilisé est lié au référentiel terrestre, considéré comme galliléen.
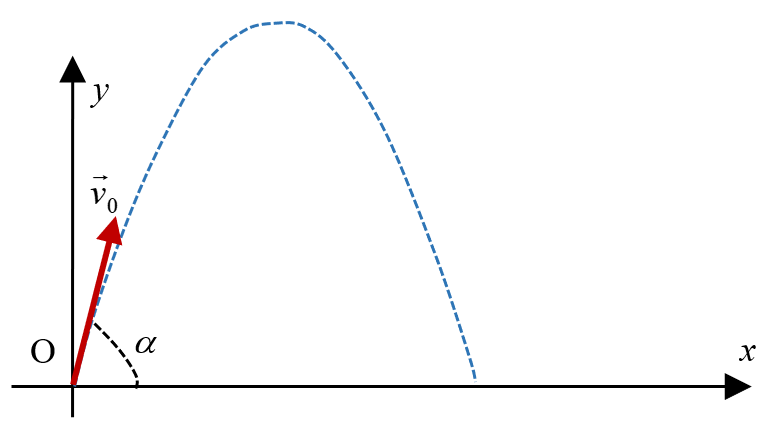
1. Donner les équations horaires littérales $*x(t)*$ et $*y(t)*$ d’un point matériel M soumis uniquement à son poids et ayant une vitesse initiale $*\vec{v}_0*$, dans la situation suivante :
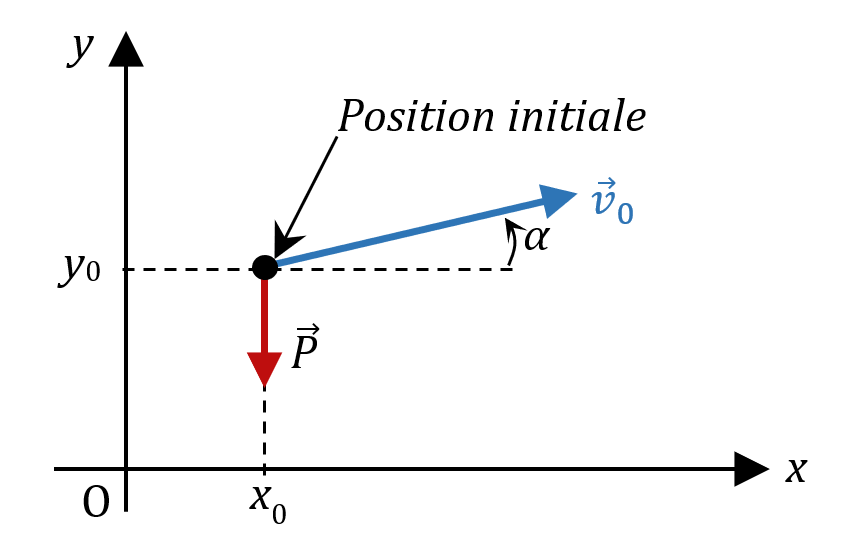
2. Application : à quelle distance retombe une pierre lancée avec une vitesse initiale de 50 km·h-1, un angle de 40°, à une distance de 2,0 m du sol ?
3. Même question, même conditions initiales, mais on se place maintenant sur la Lune, où $*g*$ vaut 1,6 N·kg-1
Correction
1. Ici, le système, le repère et le référentiel sont déjà définis.
Comme chaque fois, suivez la méthode indiquée dans l’exercice sur le Rafale.
Bilan des forces : facile ! L’énoncé le donne. Il n’y a que le poids. $* \sum \vec{F}_{ext} = \vec{P} *$. Donc, d’après la RFD : $µ \begin{aligned} m\vec{a} &= \vec{P} \\ m\vec{a} &= m\vec{g} \\ \vec{a} &= \vec{g} \\ \end{aligned} µ$ On a donc maintenant les coordonnées du vecteur accélération : $µ \vec{a} \begin{pmatrix} \begin{aligned} a_x &= 0 \\ a_y &= -g \end{aligned} \end{pmatrix} µ$
Vecteur vitesse : on intègre le vecteur accélération. Il apparaît des constantes d’intégration qui sont les coordonnées du vecteur vitesse initiale $*\vec{v}_0*$, c’est à dire $*v_{0x} = v_0 \cos \alpha*$ et $*v_{0y} = v_0 \sin \alpha*$ $µ \vec{v} \begin{pmatrix} \begin{aligned} v_x &= v_0 \cos \alpha \\ v_y &= -gt + v_0 \sin \alpha \end{aligned} \end{pmatrix} µ$
Vecteur position : on intègre le vecteur position. Les constantes d’intégration sont les coordonnées du vecteur position initiale $*x_0*$ et $*y_0*$. $µ \overrightarrow{OM} \begin{pmatrix} \begin{aligned} x &= v_0 \cos \alpha ·t + x_0 \\ y &= - \frac 12 gt^2 + v_0 \sin \alpha ·t + y_0 \end{aligned} \end{pmatrix} µ$
Et voilà !
2. Pour répondre à cette question, il faut d’abord trouver à quelle date $*t*$ la balle touche le sol (et donc $*y*$ = 0), puis, connaissant $*t*$, on calcule la position $*x*$ de la balle, en choisissant $*x_0*$ = 0, c’est à dire en plaçant l’origine du repère à l’endroit d’où on lance la balle.
Pour trouver le temps $*t*$ auquel la balle touche le sol, il suffit de résoudre $*- \frac 12 gt^2 + v_0 \sin \alpha ·t + y_0 = 0*$, avec $*y_0*$ = 2,0 m et $*v_0*$ convertie en m·s-1 (13,9 m·s-1). On trouve $*t*$ = 2,02 s, puis on en déduit $*x*$ = 21,5 m.
Remarque : soyez méthodique et rigoureux pour le calcul. Servez-vous intelligemment de votre calculatrice. Par exemple, stockez dans la variable $*a*$ la valeur de $* - \frac 12 g*$, puis dans la variable $*b*$ la valeur $*v_0 \sin \alpha*$ et enfin dans $*c*$ la valeur 2. Calculez ensuite le discriminant en utilisant ce que vous savez déjà : $*\Delta = \sqrt{b^2 - 4ac}*$. Stockez cette valeur dans la variable $*d*$. Puis calulez les solutions de l’équation de la même manière.
3. C’est le même calcul, mais avec une valeur différente pour $*g*$. On trouve $*t*$ = 11,4 s pour la date d’impact au sol, et une distance de 121 m pour le point d’impact.
🛑 Il est capital que vous sachiez refaire cet exercice vite et bien ! Et pas à peu près ! Vous devez savoir dérouler rigoureusement votre raisonnement aussi bien que son écriture mathématique. Je peux vous spoiler le sujet du prochain devoir : il y aura ça dedans… 😁
Forme du mouvement
Si l’objet à une vitesse initiale nulle ou ayant même direction (mais pas forcément même sens) que la force à laquelle il est soumis, sa trajectoire sera rectiligne. C’est le cas par exemple si vous lachez une balle sans vitesse initiale, ou si vous la lancez verticalement vers le haut ou vers le bas.
Dans tous les autres cas, le mouvement de l’objet sera parabolique.
Mais dans tous les cas, le raisonnement et les calculs pour trouver $*x(t)*$ et $*y(t)*$ restent strictement les mêmes.
Équation de la trajectoire
Parfois, il est utile de disposer de l’équation de la trajectoire, c’est-à-dire $*y(x)*$, plutôt que des équations horaires position $*x(t)*$ et $*y(t)*$.
Cette équation est facile à trouver. Le truc, c’est d’exprimer $*t*$ en fonction de $*x*$, puis d’injecter cette expression dans $*y(t)*$.
Vous avez trouvé les équations horaires suivantes dans l’exercice précédent : $µ \begin{aligned} x(t) &= v_0 \cos \alpha · t + x_0 \\ y(t) &= - \frac 12 gt^2 + v_0 \sin \alpha ·t + y_0 \end{aligned} µ$
Si on exprime $*t*$ en fonction de $*x*$, on obtient : $µ t(x) = \frac{x-x_0}{v_0 \cos \alpha} µ$
On injecte maintenant cette expression de $*t*$ dans l’équation $*y(t)*$ : $µ y(x) = - \frac 12 g· \left(\frac{x-x_0}{v_0 \cos \alpha}\right)^2 + v_0 \sin \alpha ·(\frac{x-x_0}{v_0 \cos \alpha}) + y_0 µ$
On peut encore faire une petite simplification. Vous vous souvenez que $* \frac {\sin \alpha}{\cos \alpha} = \tan \alpha*$, j’espère… Donc : $µ y(x) = - \frac 12 g· \left(\frac{x-x_0}{v_0 \cos \alpha}\right)^2 + \tan \alpha ·(x-x_0) + y_0 µ$
Et si on a un champ électrique ?
Si on a une charge ponctuelle $*q*$ dans un champ électrique $*\vec{E}*$ et qu’on néglige le poids de la particule (souvenez-vous, on en a déjà parlé plus haut), alors la RFD nous donne : $µ \begin{aligned} \vec{F}_e &= m\vec{a} \\ q\vec{E} &= m\vec{a} \\ \vec{a} &= \frac {q\vec{E}}m \end{aligned} µ$
Du coup, ce n’est pas très différent. Au lieu d’avoir $*a=g*$, on a $*a=\frac{qE}m*$. Tout le reste est identique.
Mouvement dans un champ électrique
On place un électron dans champ électrique $*\vec{E}*$ d’intensité $*E*$ = 1,0 kV·m-1. La vitesse initiale de l’électron est négligeable.
Données
- charge de l’électron = $*-e*$ = $*-*$1,60·10-19 C
- masse de l’électron = $*m_e*$ = 9,11·10-31 kg
1. Vérifier que le poids de l’électron est négligeable devant la force électrique qui s’applique sur lui.
2. En combien de temps parcourt-il 50 cm ?
3. Calculer la vitesse de l’électron après ces 50 cm.
Correction
1. $*P = mg = *$ 8,9·10-30 N et $*F_e = |q|E = *$ 1,6·10-16 N. On voit qu’il y a 13 ordres de grandeur de différence !!! Le poids est complètement négligeable devant la force électrique.
2. On choisit un axe $*\mathrm{O}x*$ dans la direction du mouvement (qui est rectiligne), l’origine de l’axe étant la position initiale de l’électron. (C’est pas obligé, mais c’est ce qu’il y a de plus simple.
Le référentiel est le référentiel terrestre.
La seule force (non négligeable) qui s’applique à l’électron est la force électrique. Donc la RFD nous donne :
$µ a_x = \frac {eE}m µ$
On intègre l’accélération pour trouver la vitesse. La vitesse initiale est nulle, donc :
$µ v_x = \frac {eE}m t µ$
On intègre la vitesse pour trouver la coordonnée de position $*x*$ de l’électon. $*x_0*$ = 0, donc :
$µ x = \frac 12 \frac {eE}m t^2 µ$
On veut connaître le temps au bout duquel $*x*$ = 0,50 m.
$µ t = \sqrt {\frac{2mx}{eE}} = 7,55·10^{-8} \; \text{s} µ$
3. Il suffit de calculer $*v*$ pour $*t*$ = 7,55·10-8 s.
$*v*$ = 1,33·107 m/s (environ 4,4 % de la vitesse de la lumière).
Accélérateur de particules
- Discuter de l’influence des grandeurs physiques sur les caractéristiques du champ électrique créé par un condensateur plan, son expression étant donnée.
- Décrire le principe d’un accélérateur linéaire de particules chargées.
On a vu l’année dernière qu’une charge électrique crée autour d’elle un champ électrique. Ce champ électrique pointe vers les charges négatives ou « fuient » les charges positives.
Pour accélérer des particules de manière contrôlée (on reparlera plus tard de l’intérêt de faire ça), il faut un champ électrique uniforme, c’est à dire identique en tout point de l’espace (au moins dans un petit espace). Alors, comment fait-on ça ? Eh bien avec un…
Condensateur plan
Un condensateur plan, c’est simplement deux plaques métalliques placées face-à-face, distante de $*d*$, connectées chacune à une borne d’un générateur dont la tension vaut $*U*$.
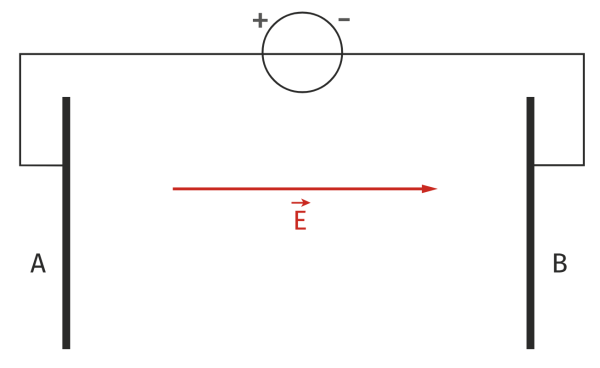
Dans l’espace délimité par les plaques, il règne un champ électrique uniforme $*\vec{E}*$ dont l’intensité vaut : $µ E = \frac Ud µ$
Remarquez que le champ électrique est orienté du ⊕ vers le ⊖.
Principe de l’accélérateur de particule
Un accélérateur linéaire de particules (il y a d’autres types d’accélérateur, dont on ne parlera pas) sert à communiquer une vitesse (généralement importante) à des particules chargées (électrons, protons, ions), et donc à augmenter son énergie (à quoi ça sert ? Attendez, on y vient plus tard).
L’idée est de faire en sorte que ces particules traversent plusieurs zones où règnent un champ électrique uniforme. À chaque passage dans une zone où il y a un champ électrique, la vitesse de la particule augmente.
Parce qu’au-delà d’une certaine valeur de champ électrique, les électrons de la plaque métallique chargée négativement sont tellement attirés par la plaque positive qu’ils quittent tout simplement leur plaque d’origine pour aller sur la plaque positive. Donc on est forcément limité au niveau de l’intensité du champ électrique.
Alors concrètement, comment on fait ça ? Eh bien c’est là qu’on peut être émerveillé par l’astuce des physiciens ! 😎 😁
Voici une animation qui explique le fonctionnement d’un accélérateur linéaire de particules :

Un accélérateur linéaire de particule est composé de tubes métalliques de longueur variable (ils sont de plus en plus grands), chacun étant connecté à une des deux bornes d’un générateur de tension alternative.
À l’intérieur du tube, il n’y a pas de champ électrique, parce que le tube est conducteur.
Par contre, entre les tubes il existe un champ électrique car, regardez-bien, les tubes sont alternativement connectés à l’une ou l’autre bornes du générateur. Ils ont donc la polarité inverse de celle de leurs voisins.
La fréquence de la tension et la longueur des tubes sont calibrées pour que, à chaque fois que la particule sort d’un tube, le champ électrique soit celui qu’il faut pour qu’elle accélère jusqu’au prochain tube. Je vous laisse réflechir au fait qu’un tel dispositif ne pourrait pas marcher avec une tension continue. 😊
Du coup, plus il y a d’étages dans l’accélérateur, plus la particule va vite, sans qu’il y ait besoin d’un champ électrique déraisonnablement intense.
Vous le voyez venir, le sujet d’exercice, là ? 😁
Accélérateur de particule
On dispose d’une source de protons et d’un générateur de tension carrée de fréquence 1,0 MHz et de tension maximale $*U*$ = 210 V (la tension vaut +210 V pendant 0,5 µs, puis -210 V pendant 0,5 µs, et ainsi de suite). On dispose également de tubes conducteurs de diamètre adéquat pour réaliser notre accélérateur. On peut les découper à la longueur que l’on souhaite. On veut réaliser un accélérateur comportant 5 tubes consécutifs séparés d’une longueur de $*d*$ = 5,0 cm.
On admet que le champ électrique qui règne entre chaque tube se calcule de la même manière que celui d’un condensateur plan.
À $*t*$ = 0, un proton est émis par la source avec une vitesse initiale négligeable. Le générateur vient de basculer dans un état de tension telle qu’il provoquera une accélération du proton (disons + 210 V).
Données
- masse du proton : $*m_p*$ = 1,67·10-27 kg
- charge élémentaire : $*e*$ = 1,60·10-19 C
1. Trajet jusqu’au premier tube
1.1. À quelle date ce proton va-t-il entrer dans le premier tube ?
1.2. Quelle sera sa vitesse ?
1.3. La fréquence du champ électrique est-elle appropriée ?
2. Traversée du premier tube
Quelle doit être la longueur du premier tube pour que le proton arrive à la sortie de celui à $*t*$ = 0,75 µs ? Combien de temps reste-t-il alors au proton avant que le champ électrique ne s’inverse ?
3. Deuxième phase d’accélération
3.1. Le proton arrive à la sortie du premier tube à $*t*$ = 0,75 µs. Donner la date et la vitesse avec laquelle il entre dans le deuxième tube, distant de 5,0 cm du premier.
3.2. Quelle devra être la longueur du deuxième tube pour que le proton en sorte à $*t*$ = 1,25 µs ?
Correction
1.1. On définit un axe $*\mathrm{O}x*$ dont l’origine coïncide avec la sortie de la source et orienté dans le sens du mouvement du proton.
Lorsque le proton sort, il a une accélération :
$µ a = a_x = \frac {eE}{m} = \frac {eU}{md} µ$
Sa vitesse est donc : $µ v_x(t) = at µ$ et sa position est : $µ x(t) = \frac 12 at^2 µ$ Les constantes d’intégration sont nulles car à $*t*$ = 0, le proton n’a pas de vitesse initiale et il se trouve sur l’origine de l’axe.
Remarque : je ne détaille pas les calculs, vous l’avez déjà fait plusieurs fois. Mais en évaluation, il faut détailler davantage, bien-sûr.
On cherche à quelle date $*t_e*$ le proton entre dans le tube, autrement dit : quand est-ce que $*x*$ = $*d*$ = 0,05 m. $µ t_e = \sqrt{\frac {2d^2m}{eU}} = 5,0·10^{-7} \; \text{s} µ$
1.2. $*v(t_e)*$ = $*v_{1}*$ = 2,0·105 m·s-1
1.3. La tension bascule à $*t*$ = 0,50 µs, date à laquelle le proton entre dans le tube. Si elle avait changé avant, cela aurait freiné le proton. Mais là, c’est bon. Juste à la limite, mais c’est bon quand-même.
2. Dans le tube, le proton n’est plus soumis à aucune force. Il est donc en MRU. Il doit sortir du tube à $*t_s*$ = 0,75 µs. La distance qu’il doit parcourir vaut donc $*\Delta x*$ = $* v_1·\Delta t *$ = 2,0·105×0,25·10-6 = 0,050 m.
Le tube doit donc avoir une longueur de 5,0 cm.
3.1. Là, ça se corse un peu… 😅 Si vous n’y êtes pas arrivé, ce n’est pas grave. Les calculs ne sont pas compliqués, mais il faut être très rigoureux et structuré dans son raisonnement pour ne pas s’y perdre. Essayez au moins de comprendre la correction.
À $*t*$ = 0,75 µs, le proton sort du tube n°1 avec la vitesse $*v_1*$, en $*x*$ = 0,10 m. Il est soumis à la même accélération $*a*$ qu’avant son entrée dans le tube n°1, car le champ électrique est le même.
Pour se simplifier les calculs et la vie, on peut prendre :
- la date de sortie du tube n°1 $*t*$ = 0,75 µs comme nouvelle origine des dates $*t'*$ ;
- la sortie du tube n°1 comme nouvelle origine des abscisses $*x'*$.
$µ \begin{aligned}
v(t') &= at' + v_1 \\
x'(t') &= \frac 12 at'\,^2 + v_1t
\end{aligned} µ$
On cherche à savoir pour quelle valeur de $*t'_e*$ le proton entre dans le deuxième tube, soit $*x'*$ = $*d*$
On doit donc résoudre une équation du deuxième degré…
$µ \frac 12 a{t'_e}^2 + v_1t'_e - d = 0 µ$
On trouve le discriminant $*\Delta*$ = 8,05·1010 m2·s-2 et une durée de traversée de l’espace entre le tube 1 et le tube 2 de $*t'_e*$ = 0,21 µs.
Donc le proton entre dans le tube n°2 0,21 µs après être sortie du tube n°1, c’est-à-dire à $*t*$ = 0,75 + 0,21 = 0,96 µs.
3.2. Le proton doit ressortir du tube n°2 à la date $*t'_s*$ = 1,25 µs. La traversée du tube doit donc durer 1,25 - 0,96 = 0,29 µs.
À quelle vitesse entre-t-il dans le tube n°2 ? $*v(t’_e) = at'_e + v_1 = v_2*$ = 2,84·105 m·s-1.
La longueur du tube n°2 doit être la distance parcourue par l’électron à la vitesse $*v_2*$ pendant un durée de 0,29 µs, soit : 0,082 m.
On peut continuer les calculs en tenant compte que le proton dont sortir du tube suivant 0,5 µs pour rester synchronisé avec les variations de tension. On trouve pour le troisième tube une longueur de 11,9 cm, puis 14,7 cm pour le suivant, etc… C’est une bonne occasion d’automatiser les calculs sur un tableur.
Pour un accélérateur de 20 m de long environ, on trouve qu’il faut 44 tubes, le dernier mesurant 61 cm et le proton en sort avec une vitesse de 1,33·106 km·s-1 environ. Ce qui est très peu.
À quoi ça sert ?
À plein de chose… 😄
Si vous accélérez des électrons, vous pouvez générer des rayons X, créer un microscope électronique, analyser la structure d’un cristal, faire un écran cathodique (vous savez, les vieilles télés qui faisant 1 m de profondeur…)
Si vous accélérez des particules chargées plus lourdes (protons où ions), vous pouvez bombarder de la matière pour voir ce qu’il y a dans les atomes, voire dans le noyau des atomes. Des collisions très énergétiques entre particules peuvent faire apparaître des antiparticules ou des particules dont la durée de vie est extrêmement brève. Vous pouvez aussi provoquer des réactions nucléaires pour obtenir des isotopes radioactifs qui peuvent servir, entre autres choses, en médecine. Bref, il y a un paquet d’applications qui font que les accélérateurs de particules sont des dispositifs courants.
Le plus grand accélérateur au monde est le LHC. Il fait 27 km de long et propulse des protons à une vitesse de 99,9999991% de la vitesse de la lumière
À plein de chose… 😄
Si vous accélérez des électrons, vous pouvez générer des rayons X, créer un microscope électronique, analyser la structure d’un cristal, faire un écran cathodique (vous savez, les vieilles télés qui faisant 1 m de profondeur…)
Si vous accélérez des particules chargées plus lourdes (protons où ions), vous pouvez bombarder de la matière pour voir ce qu’il y a dans les atomes, voire dans le noyau des atomes. Des collisions très énergétiques entre particules peuvent faire apparaître des antiparticules ou des particules dont la durée de vie est extrêmement brève. Vous pouvez aussi provoquer des réactions nucléaires pour obtenir des isotopes radioactifs qui peuvent servir, entre autres choses, en médecine. Bref, il y a un paquet d’applications qui font que les accélérateurs de particules sont des dispositifs courants.
Aspects énergétiques
- Exploiter la conservation de l’énergie mécanique ou le théorème de l’énergie cinétique dans le cas du mouvement dans un champ uniforme.
Presque rien de nouveau ici par rapport au chapitre P5 de première. On va commencer par un petit TP, et je vous présenterai la seule nouveauté en fin de paragraphe
Rappels de première
Énergie cinétique
| $µ E_c = \frac 12 mv^2 µ$ | $*m*$ : masse (kg) $*v*$ : vitesse (m·s-1) |
Énergie potentielle de pesanteur
| $µ E_{pp} = mgz µ$ | $*m*$ : masse (kg) $*g*$ : intensité du champ de pesanteur (N·kg-1) $*z*$ : altitude (m) |
Énergie mécanique
C’est la somme des différentes énergies potentielles. Rappelez-vous, je vous ai dit en première qu’il y avait plusieurs formes d’énergies potentielles. On n’a vu ensemble que l’énergie potentielle de pesanteur. Mais il y a également l’énergie potentielle électrique. J’en parlerai plus loin, dans la partie sur les nouveautés de cette année.
Travail d’une force
Le travail d’une force, c’est l’énergie que cette force communique au système étudié lors de son déplacement. Un travail peut être négatif si la force s’oppose au mouvement. Par exemple, le travail des forces de frottements est toujours négatif.
Le travail $*W*$ d’une force constante $*\vec{F}*$ sur un trajet rectiligne $*\vec{d}*$ se calcule par la relation :
$*\vec{F}·\vec{d}*$ est le produit scalaire de ces deux vecteurs. $*\vec{F}·\vec{d} = F·d·\cos (\theta) *$ avec $*\theta*$ l’angle entre les deux vecteurs.
Si le travail d’une force est positif, on dit qu’il est moteur.
S’il est négatif, on dit qu’il est résistant.
Conservation de l’énergie mécanique
Qu’est-ce qu’une force conservative ? C’est une force qui peut être associée à une énergie potentielle. Vous en connaissez seulement deux (et ça ne changera pas cette année) : le poids (associée à l’énergie potentielle de pesanteur $*E_{pp}*$) et la force électrique (associée à l’énergie potentielle électrique $*E_{pe}*$ dont je reparlerai plus bas.
Par conséquent, la variation d’énergie mécanique d’un système est égale à la somme du travail des forces non-conservatives qui s’appliquent sur ce sytème.
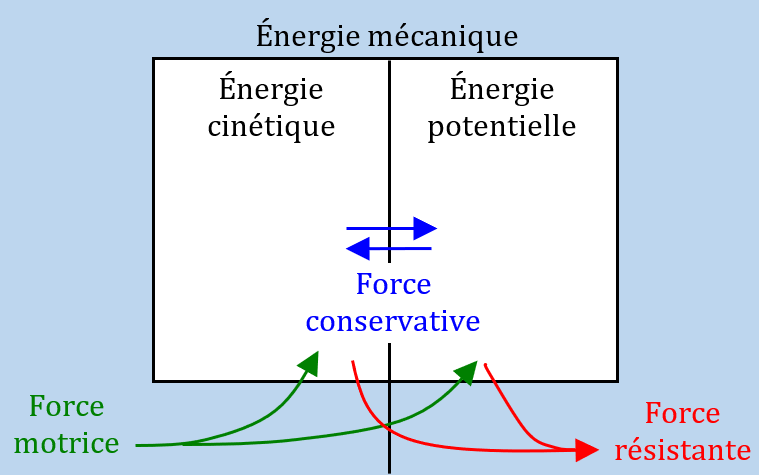
Le travail d’une force conservative ne fait que transformer l’énergie cinétique en énergie potentielle ou inversement. L’énergie mécanique du système est conservée.
Le travail d’une force motrice augmente l’énergie mécanique du système.
Le travail d’une force résistante diminue l’énergie mécanique du système.
Théorème de l’énergie cinétique
Allez, trève de rappel, place au TP. 😊
TP Énergie mécanique
- Utiliser des capteurs ou une vidéo pour déterminer les équations horaires du mouvement du centre de masse d’un système dans un champ uniforme.
- Étudier l’évolution des énergies cinétique, potentielle et mécanique.
- Capacité numérique : représenter, à partir de données expérimentales variées, l’évolution des grandeurs énergétiques d’un système en mouvement dans un champ uniforme à l’aide d’un langage de programmation ou d’un tableur.
Objectif : à partir de cette vidéo, réalisez un graphique avec Python, qui montre :
- la trajectoire de la balle $*y(x)*$ sous forme de points successifs ;
- l’énergie cinétique $*E_c*$ de la balle au cours du mouvement (courbe continue bleue) ;
- l’énergie potentielle de pesanteur $*E_{pp}*$ de la balle au cours du mouvement (courbe continue verte) ;
- l’énergie mécanique $*E_m*$ de la balle au cours du mouvement (courbe continue rouge).
Trouver les fonctions y(t) et x(t) sur Excel
Modéliser les résultats de votre pointage $*x(t)*$ et $*y(t)*$ sur Excel
Générer les grandeurs nécessaires sur Python
Plutôt que d’importer les valeurs modélisées dans Python, nous allons les lui faire calculer à partir des modèles trouvés par Excel.
D’abord, nous avons besoin de créer un tableau contenant les valeurs de $*t*$. Le code ci-dessous
t = [0.04*i + 0.36 for i in range(26)]
permet de créer une liste de 26 valeurs de $*t*$, commençant à 0,36 s et avec une incrémentation de 0,04 s. À vous de l’adapter à vos valeurs de $*t*$
Ensuite, si vous voulez générer vos valeurs de $*x*$ à partir du modèle trouvé par Excel (par exemple $*x = 2,5t + 1*$), vous pouvez utiliser le code ci-dessous.
x = [2.5*i + 1 for i in t]
Ce code permet de créer une liste appelée $*x*$ dont chaque élément est calculé à partir des valeurs de $*t*$ selon le calcul que vous lui indiquez. Très utile à retenir.
Tracer du graphique
Comme les grandeurs $*y*$ d’une part, et $*E_c*$ , $*E_p*$, $*E_m*$ d’autre part n’ont rien à voir, vous allez tracer un graphique ayant deux axes des ordonnées différents. Référez-vous à la section Python pour savoir comment faire.
N’hésitez pas à aller jeter un coup d’œil sur la page Techniques de TP si vous avez un trou de mémoire… 😊
Conclusion
Qu’est ce que ce graphique met en évidence ?
Éléments de correction
Ce fichier txt contient les résultats du pointage. Après modélisation, on trouve :
- $* y(t) = -4,6967t^2 + 5,4706t + 2,4489 *$
- $* x(t) = 4,4767t + 0,4405 *$
On estime la masse du ballon en cherchant sur internet : environ 600 g. La valeur exacte n’a de toute façon pas d’importance pour arriver à la conclusion.
Voici un code Python possible. Celui-ci est le plus court possible, mais on pourrait y rajouter des éléments de décoration, comme la légende des différentes courbes et une grille. Si ça vous intéresse, je mets un code plus élaboré à la fin de la correction.
t = [0.04*i for i in range(26)]
x = [4.5007*i + 0.6191 for i in t]
y = [-4.7153*i**2 + 5.5117*i + 2.4912 for i in t]
vx = [4.5007 for i in t]
vy = [-2*4.7153*i + 5.5117 for i in t]
v = [(vx[i]**2 + vy[i]**2)**0.5 for i in range(26)]
Ec = [0.5*0.6*i**2 for i in v]
Epp = [0.6*9.8*i for i in y]
Em = [Ec[i] + Epp[i] for i in range(26)]
import matplotlib.pyplot as plt
fig, axe1 = plt.subplots()
axe1.set_xlabel('x (m)')
axe1.set_xlim(0, 5.5)
axe1.set_ylabel('hauteur (m)', color='black')
axe1.set_ylim(0, 5)
axe2 = axe1.twinx()
axe2.set_ylabel('Énergie (J)', color='red')
axe2.set_ylim(0, 35)
axe1.plot(x, y, 'ko', ms=7)
axe2.plot(x, Ec, 'b-')
axe2.plot(x, Epp, 'g-')
axe2.plot(x, Em, "r-")
plt.show()
Et voici le graphique obtenu :
Conclusion
On voit que l’énergie mécanique (courbe rouge) du ballon reste constante au cours du mouvement. On remarque tout de même une légère déformation de cette courbe. Peut-être due aux aberrations géométriques de la lentille de la caméra.
Code Python plus élaboré
t = [0.04*i for i in range(26)]
x = [4.5007*i + 0.6191 for i in t]
y = [-4.7153*i**2 + 5.5117*i + 2.4912 for i in t]
Epp = [0.6*9.8*i for i in y]
vx = [4.5007 for i in t]
vy = [-2*4.7153*i + 5.5117 for i in t]
v = [(vx[i]**2 + vy[i]**2)**0.5 for i in range(26)]
Ec = [0.5*0.6*i**2 for i in v]
Em = [Ec[i] + Epp[i] for i in range(26)]
import matplotlib.pyplot as plt
fig, axe1 = plt.subplots()
axe1.set_xlabel('x (m)')
axe1.set_xlim(0, 5.5)
axe1.set_ylabel('hauteur (m)', color='black')
axe1.set_ylim(0, 5)
axe2 = axe1.twinx()
axe2.set_ylabel('Énergie (J)', color='firebrick')
axe2.set_ylim(0, 35)
for valeur in axe2.get_yticklabels(): valeur.set_color('firebrick')
axe1.plot(x, y, 'ko', ms=7, label = "Trajectoire balle")
axe2.plot(x, Ec, 'b-', label = "Ec")
axe2.plot(x, Epp, 'g-', label = "Epp")
axe2.plot(x, Em, color="firebrick", linestyle="--", label = "Em")
axe1.spines['top'].set_color('none')
axe2.spines['top'].set_color('none')
axe1.grid(True, linestyle="--")
axe1.legend(loc="lower left")
axe2.legend(loc="lower right")
plt.show()
Graphique obtenu avec ce code :
Voici quelques exercices sur le travail de forces et la conservation ou non de l’énergie mécanique
Travail d’une force constante
Une autre manière de résoudre l’exercice sur le décollage du rafale.
Le Rafale a une masse de 23,7 t. Il dispose de deux turbos réacteurs d’une poussée unitaire de 50 kN. Sa vitesse de décollage est de 213 km·h-1. Le porte-avion Charles de Gaulle comporte une piste horizontale de 195 m. On négligera les frottements tout au long de cet exercice.
1.a. Calculer le travail de la force de poussée des réacteurs sur la longueur de la piste. Comment peut-on qualifier ce travail ?
1.b. Y a-t-il d’autres forces qui travaillent lors de ce déplacement ?
2.a. En quelle forme d’énergie se transforme le travail de cette force ?
2.b. L’énergie mécanique de l’avion est-elle constante lors de ce déplacement ?
3. Montrer, sans utiliser la RFD, que l’avion ne peut décoller sur une distance aussi courte.
Correction
1.a Comme la force de poussée $*\vec{F}*$ est constante et que le trajet est rectiligne, on peut calculer ce travail par le relation :
$µ W_d(\vec{F}) = \vec{F}·\vec{d} µ$
où $*\vec{d}*$ est le vecteur déplacement. L’angle entre $*\vec{F}*$ et $*\vec{d}*$ est nul, d’où $* W_d(\vec{F}) = F·d =*$ 100·103×195 = 19,5 MJ.
Ce travail est positif, il est donc moteur.
1. Le poids et la réaction de la piste sont perpendiculaires au déplacement, donc ces forces ne travaillent pas. Et il n’y a pas d’autres forces, puisque les frottements sont négligés.
2.a. En énergie cinétique, car la force de poussée ne fait pas varier l’altitude de l’avion (dans sa phase d’accélératioin) donc son énergie potentielle de pesanteur reste constante.
2.b. L’énergie cinétique de l’avion augmente mais son énergie potentielle reste constante, donc son énergie mécanique augmente.
3. Au bout de la piste, l’énergie cinétique de l’avion vaut 19,5 MJ. On peut donc en déduire sa vitesse : $*v = \sqrt{2E_c/m}*$ = 40,6 m·s-1. Cette valeur est inférieure aux 213 km·h-1 (59,2 m·s-1) nécessaires. Donc on retrouve bien que l’avion ne peut pas décoller.
Lancer de balle
Une balle est lancée vers le haut, dans une direction parfaitement verticale, à partir d’une hauteur $*h*$ = 2,0 m et avec une vitesse initiale de 3,0 m·s-1. Les forces de frottement seront négligées.
Sans utiliser la RFD, déterminer quelle est la hauteur maximale atteinte par la balle, et quelle est sa vitesse au moment où elle touche le sol.
Correction
Tout au long du mouvement, on se sert dans la conservation de l’énergie. En effet, dans cette situation, l’énergie mécanique se conserve car la seule force qui travaille est le poids qui est une force conservative.
Donc entre deux situations (1) et (2), on a $*E_{m1} = E_{m2}*$.
L’origine de l’altitude est prise au sol.
Situation initiale : $*E_{ci} = \frac 12 mv_i^2*$ et $*E_{ppi} = mgz_i*$. On ne peut pas calculer numériquement ces valeurs car on ne connaît pas la masse de la balle, mais on s’en fiche car on peut ensuite tout simplifier par la masse.
Au sommet de la trajectoire, $*E_c = 0*$, donc $*mgz_{max} = \frac 12 mv_i^2 + mgz_i*$. D’où : $µ z_{max} = \frac 1{2g} v_i^2 + z_i = 2,46 \; \mathrm{m} µ$
Au moment de l’impact au sol, $*E_{pp} = 0*$, donc $* \frac 12 mv^2 = \frac 12 mv_i^2 + mgz_i*$. D’où : $µ v = \sqrt{v_i^2 + 2gz_i} = 6,95 \; \mathrm{m·s^{-1}} µ$
Saut en parachute
Un parachutiste de masse $*m*$ = 80 kg suit une trajectoire rectiligne du point A au point B comme montré sur la figure ci-dessous. Durant cette chute, sa vitesse est constante et vaut $*v*$ = 1,5 m·s-1.
Données : AB = 100 m et $*\theta*$ = 10°.
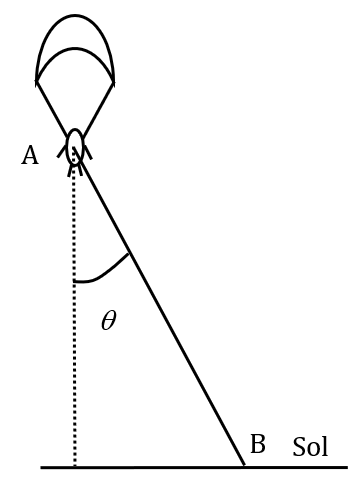
1. Exprimer le travail du poids en fonction de $*\theta*$, $*m*$, $*g*$ et AB.
2. Démontrer que ce travail peut s’écrire $*W_{AB} (\vec{P}) = mg(z_A - z_B)*$.
3. Calculer la valeur du travail du poids sur ce parcours.
4. Calculer la variation d’énergie mécanique du parachutiste entre le point A et le point B juste avant qu’il ne touche le sol (altitude négligeable mais $*v_B*$ = 1,5 m·s-1).
5. Pourquoi cette énergie mécanique n’est-elle pas constante ? En déduire la valeur du travail des forces de frottements.
Correction
1. On applique bêtement la formule du cours : $*W_{AB}(\vec{P}) = mg·\mathrm{AB}·\cos \theta *$
2. Il suffit de remarquer que $* \mathrm{AB}·\cos \theta *$ correspond à la hauteur de A par rapport au sol, autrement dit $*z_A - z_B*$.
3. 77,3 kJ
4. Énergie mécanique initiale : 77,4 kJ ; énergie mécanique au moment de toucher le sol : 90 J. Donc $*\Delta E_m*$ = -77,3 kJ.
5. Elle n’est pas constante à cause des frottements. Travail des forces de frottement : $*W(\vec{f}) = \Delta E_m*$.
Luge (bis)
Un enfant descend une pente en luge.
Données
- Vitesse en A : $*v_A \simeq*$ 0
- Vitesse en B : $*v_B*$ = 5 m·s-1
- Dénivelé : $*z_A – z_B*$ = $*h*$ = 5 m
- Angle de la pente avec l’horizontal : $*\alpha*$ = 10°
- Masse du système {luge + enfant} : $*m*$ = 40 kg
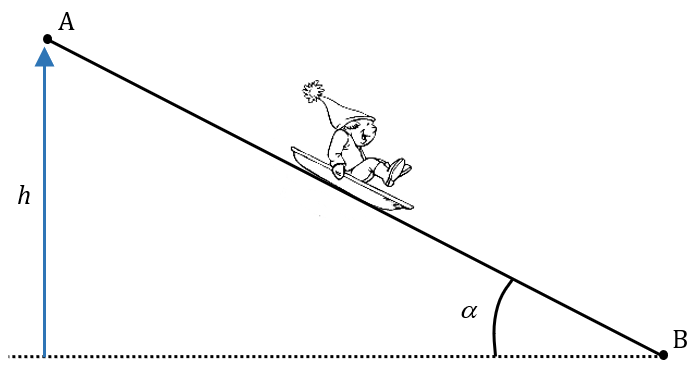
1. Quelle serait sa vitesse en B si les frottements étaient négligeables ?
2. Trouver la valeur moyenne des forces de frottements qui s’exercent sur la luge au cours de la descente.
Correction
1. Sans frottements, il n’y a que le poids $*\vec{P}*$ et la réaction de la piste $*\vec{R}*$. Mais $*\vec{R}*$ ne travaille pas car elle est perpendiculaire à la piste. Donc seul $*\vec{P}*$ travaille et donc l’énergie mécanique se conserve. D’où $*E_{mA} = E_{mB}*$.
Il s’en suit que : $*mgz_A = \frac 12 mv_B^2 + mgz_B*$.
$µ v_B = \sqrt{2g(z_A-z_B)} µ$
$*v_B*$ = 9,9 m·-1.
2. Le travail des forces de frottement est égal à la variation d’énergie mécanique.
$µ \Delta E_m = mgz_A - \frac 12 m v_B^2 µ$
D’où $*\Delta E_m*$ = $*-*$1460 J
La valeur « moyenne » des forces de frottements correspond à celle qu’elles auraient si elles étaient constantes sur tout le trajet. Donc, si on appelle $*f*$ cette valeur moyenne, on a : $*f·\mathrm{AB}·\cos(180°) = -1460*$.
$*\mathrm{AB}*$ = 28,8 m.
Ce qui donne $*f*$ = 50,7 N.
Énergie potentielle électrique
Lorsque vous lachez une balle dans un champ de pesanteur, elle tombe (j’espère que je ne vous apprends rien… 😁). Se faisant, elle gagne de l’énergie cinétique $*E_c*$. D’où lui vient cette énergie cinétique ? Eh bien de l’énergie potentielle de pesanteur $*E_{pp}*$ que la balle avait. Cette $*E_{pp}*$ se transforme, au cours de sa chute, en $*E_c*$.
Si vous lachez une particule chargée dans un champ électrique, elle va accélérer dans la direction du champ électrique (le sens de cette accélération dépend du signe de sa charge et du sens du champ électrique). D’où lui vient cette énergie cinétique ? Eh bien de l’énergie potentielle électrique $*E_{pe}*$ qu’a la particule chargée du fait de la présence d’un champ électrique. C’est pareil ! 😊
Mais avant de vous parler de cette $*E_{pe}*$, il faut que je vous parle du potentiel électrique. Il est dommage que cette notion ne soit jamais abordée au lycée, elle permet de comprendre simplement un certain nombre de choses dès qu’on parle d’électricité.
Le potentiel électrique, c’est un peu l’« altitude » électrique d’un point donné. Point qui peut être dans le vide aussi bien que dans la matière d’ailleurs.
Vous avez peut-être entendu l’expression « différence de potentiel » pour désigner une tension électrique. Vous savez qu’une tension électrique se mesure toujours entre deux points (ou deux bornes si on parle d’un circuit électrique, ça revient au même).
Par exemple, dire qu’il y a une tension de 6 V aux bornes d’un générateur, c’est dire que le potentiel électrique de la borne ⊕ est supérieur de 6 V au potentiel électrique de la borne ⊖.
On choisit toujours un potentiel de référence, qui vaut 0 par convention. Exactement comme on choisit une altitude de référence (le sol du labo, la surface de la table, le niveau de la mer…) qui vaut par convention 0.
Lorsqu’on parle d’un circuit électrique, on choisit généralement la borne $*-*$ comme référence des potentiels (mais ce n’est pas une obligation).
Du coup, maintenant, je peux vous donner la définition de l’énergie potentielle électrique.
| $µ E_{pe} = qV µ$ | $*q*$ : charge (C) $*V*$ : potentiel électrique (V) |
Oui, je sais, le potentiel électrique est noté $*V*$, et son unité est le volt V. C’est pas très malin comme notation 😐 , mais sachez que la notation $*U*$ est plutôt réservée à une différence de potentiel (une tension), elle aussi en volt.
Potentiel et champ électrique
Il y a un lien intime entre le champ électrique $*\vec{E}*$ et le potentiel. Vous n’avez pas besoin de le connaître et ça serait un peu long à expliquer, mais sachez que, physiquement, le champ électrique pointe dans la direction où le potentiel décroît le plus rapidement.
Du coup, un proton (de charge $*+e*$ donc) qui se déplace de 1 m dans la direction et le sens d’un champ électrique d’intensité $*E*$ = 1000 V·m-1 est passé d’un point initial A à un point B dont le potentiel électrique est inférieur de 1000 V.
Par conséquent, son énergie potentielle est passée de $*E_{pe}(A) = e·V_A*$ à $*E_{pe}(B) = e·V_B*$.
Et sa variation d’énergie potentielle électrique (c’est ça qui nous intéresse concrètement) vaut :
$µ \Delta E_{pe} = eV_B - eV_A = e·(-1000)µ$
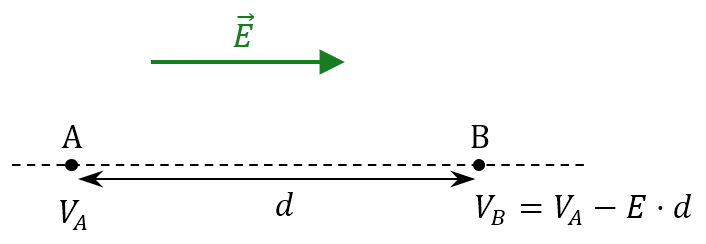
Dans cette situation, si on ne prend en compte que la force électrique (on a vu précédemment dans le cours que c’était justifié de négliger le poids du proton), qui est une force conservative, alors l’énergie mécanique du proton se conserve au cours de son mouvement. Ce qui implique que l’$*E_{pe}*$ perdue est égale à l’$*{E_c}*$ gagnée.
Petite remarque au passage, ça fait -1000 eV. Ça vient de là, la définition de l’électron-volt…
Énergie potentielle électrique
1.a. Quelle est la variation d’énergie potentielle d’un électron passant de la borne – à la borne + d’un générateur ayant une différence de potentiel de 6 V entre ses bornes ?
1.b. Que devient cette énergie perdue par l’électron ?
2. Quelle est la variation d’énergie potentielle d’un proton se déplaçant dans le vide parallèlement à un champ électrique d’intensité 1000 V·m-1, sur une distance de 50 cm, vers les potentiels négatifs ? Quelle est sa vitesse après ce déplacement si sa vitesse initiale est négligeable ?
Correction
1.a $* \Delta E_{pe} = E_{pef} - E_{pei} = -e·(6) - -e·(0) = -6e*$.
Donc $* \Delta E_{pe}*$ = -6×1,60·10-19 = -9,6·10-19 J (ou encore -6 eV).
1.b. L’électron ne se déplace pas dans le vide, il n’acquiert donc pas une grande vitesse donc pas d’énergie cinétique. Que devient cette énergie, alors ? Une partie est dissipée sous forme de chaleur (effet Joule) et une autre est transformée en « énergie utile » par le circuit électrique traversé par l’électron (énergie lumineuse s’il s’agit d’une ampoule, énergie mécanique s’il s’agit d’un moteur, etc.).
2. Il s’agit ici de la même situation que celle décrite dans le cours. $* \Delta E_{pe}*$ = -500×1,6·10-19 = -8,0·10-17 J.
D’où $*E_c*$ = 8,0·10-17 J et $*v = \sqrt {\frac {2E_c}m} =*$ 310 km·s-1.
Révision & entraînement
Prenez le temps de rédiger correctement vos réponses. Vous serez également notés là-dessus en contrôle. Suivez la méthode donnée dans l’exercice sur le décollage du Rafale.
Balle lancée vers le haut
Une balle est lancée vers le haut, dans une direction parfaitement verticale, à partir d’une hauteur de $*h*$ = 2,0 m et avec une vitesse initiale de $*v_0*$ = 3,0 m·s-1. Les forces de frottement pourront être négligées. On prendra $*g*$ = 10 m·s-2.
1.a. Au bout de combien de temps retombe-t-elle au sol à partir du moment où la balle est lâchée ?
1.b. Quelle est la hauteur maximale atteinte au cours de sa trajectoire ?
1.c. Quelle vitesse a la balle au moment de son impact avec le sol ?
2. Mêmes questions sur la lune ($*g_{\text{lune}}*$ = 1,6 m·s-2).
Correction
1.a. Le système étudié est la balle, dans le référentiel terrestre considéré comme galiléen. On étudie le mouvement sur un unique axe $*\mathrm{O}z*$ vertical orienté vers le haut, l’origine du repère est prise au niveau du sol.
Une seule force s’applique, le poids $*\vec{P}*$ de coordonnée $*P_z = -mg*$.
La RFD nous donne : $*\vec{P} = m\vec{a}*$ donc :
• $*\vec{a}(a_z = -g)*$.
On intègre $*\vec{a}*$ par rapport au temps. Comme le vecteur vitesse initale $*\vec{v}_0*$ a pour coordonnée $*v_{0z}*$ = $*v_0*$, on obtient :
• $*\vec{v}(v_z = -gt + v_0)*$
On intègre encore une fois pour obtenir le vecteur position. La position initiale est $*z_0 = h*$. Donc :
• $* \overrightarrow{OM} (z = -0,5·gt^2 + v_0t + h)*$
On cherche à savoir quand est-ce que $*z(t)*$ = 0. On résout $*-0,5·gt^2 + v_0t + h = 0*$ avec les valeurs de l’énoncé, et on obtient deux solutions : $*t_1*$ = 1,0 s et $*t_2*$ = -0,4 s. Seule la première solution a du sens.
La balle retombe donc au sol après 1,0 s.
1.b. La hauteur maximale est atteinte lorsque la vitesse de la balle est nulle. On résout $*-gt + v_0 = 0*$ et on obtient la date à laquelle la hauteur maximale est atteinte : $*t_3*$ = 0,30 s.
Puis on injecte ce temps dans l’expression de $*z(t)*$ et on obtient $*z(t_3)*$ = 2,45 m.
1.c. On sait que la balle touche le sol à $*t_1*$ = 1,0 s, on calcule $*v_z(t_1)*$ = -7 m·s-1. La valeur de la vitesse, c’est la norme du vecteur vitesse, donc $*v = \sqrt{(-7)^2} = *$ 7 m·s-1.
2. Tous les calculs sont les mêmes. Si vous avez fait des calculs littéraux (c’est qui est très recommandé), vous n’avez qu’à changer la valeur de $*g*$ pour trouver :
$*t_1*$ = 4,3 s ; hauteur maximale : 4,8 m ; vitesse d’impact : 3,9 m·s-1.
Service au tennis
Un joueur de tennis fait un service en communicant une vitesse initiale de valeur $*v_0*$ à la balle parallèlement au sol. La balle est frappée à $*h*$ = 2,30 m du sol. Elle doit passer au dessus du filet, d’une hauteur de $*h_F*$ = 91 cm, situé à $*x_F*$ = 12,0 m du joueur et doit toucher le sol avant la ligne de service, située à $*x_L*$ = 18,4 m. On négligera les frottements. On prendre $*g*$ = 9,8 m·s-2.
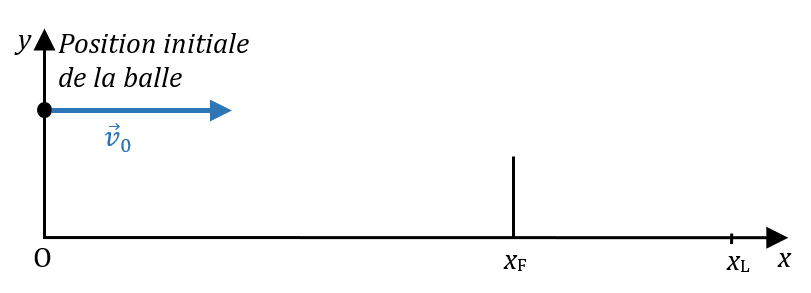
Problème : donner un encadrement de $*v_0*$, en km/h, qu’il doit communiquer à la balle pour réussir son service.
Correction
Voici une correction rapide vous permettant de vérifier vos résultats. Vous devez rédiger davantage la première partie concernant l’établissement des équations du mouvement.
Étant donné que la seule force qui s’applique au système est le poids, on a $*\vec{P} = m\vec{a}*$.
Les coordonnées du vecteur $*\vec{v}_0*$ sont : $*v_{0x} = v_0*$, $*v_{0y} = 0*$
La position initiale $*\overrightarrow {OM}_0*$ est $*x_0 = 0*$, $*y_0 = h*$.
On obtient les équations du mouvement suivantes :
$µ \vec{a} \begin{pmatrix} \begin{aligned}
a_x &= 0 \\
a_y &= -g
\end{aligned} \end{pmatrix}
\quad
\vec{v} \begin{pmatrix} \begin{aligned}
v_x &= v_0 \\
a_y &= -gt
\end{aligned} \end{pmatrix}
\quad
\overrightarrow {OM} \begin{pmatrix} \begin{aligned}
x &= v_0t \\
y &= - \frac 12 gt^2 + h
\end{aligned} \end{pmatrix}
µ$
La vitesse la plus faible doit permettre à la balle de passer juste au-dessus du filet. Pour cette vitesse, lorsque $*x = x_F*$, $*y*$ > 0,91 m (on assimile la balle à un point, donc on néglige ses dimensions).
On cherche la date $*t_F*$ à laquelle la balle est juste au-dessus du filet :
$µ t_F = \sqrt {\frac {2(h-h_F)}g } = 0,533 \; \mathrm{s} µ$
Ensuite, on cherche $*v_0*$ pour que $*x(t_F)*$ = $*x_F*$ :
$µ v_0 = \frac {x_F}{t_F} = 22,5 \; \mathrm{m·s^{-1}} µ$
Ce qui donne $*v_0 \simeq*$ 81 km·h-1.
La vitesse la plus élevée doit permettre à la balle de toucher le sol sur la ligne de service à $*x_L*$ = 18,4 m.
On cherche la date $*t_L*$ à laquelle la balle touche le sol :
$µ t_L = \sqrt {\frac {2h}g } = 0,685 \; \mathrm{s} µ$
Ensuite, on cherche $*v_0*$ pour que $*x(t_L)*$ = $*x_L*$ :
$µ v_0 = \frac {x_L}{t_L} = 26,9 \; \mathrm{m·s^{-1}} µ$
Ce qui donne $*v_0 \simeq*$ 97 km·h-1.
La chandelle au rugby
D’après un exercice de bac – Liban 2013
Au rugby, une « chandelle » désigne un coup de pied permettant d’envoyer le ballon en hauteur par dessus la ligne de défense adverse. L’objectif pour l’auteur de cette action est d’être au point de chute pour récupérer le ballon derrière le rideau défensif.
On se place dans le référentiel terrestre supposé galiléen.
Le champ de pesanteur terrestre est considéré uniforme, de valeur $*g*$ = 9,81 N·kg-1. On négligera toutes les actions dues à l’air.
Le joueur A est animé d’un mouvement rectiligne uniforme de vecteur vitesse $*\vec{v}_1*$. Afin d’éviter un plaquage, il réalise une chandelle au-dessus de son adversaire.
On définit un repère (O, $*\vec{i}*$, $*\vec{j}*$ ) :
- origine : position initiale du ballon ;
- vecteur unitaire $*\vec{i}*$ de même direction et de même sens que $*\vec{v}_1*$ ;
- vecteur unitaire $*\vec{j}*$ vertical et vers le haut.
À l’instant $*t*$ = 0, le vecteur vitesse du ballon fait un angle $*\alpha*$ égal à 60° avec l’axe $*\mathrm{O}x*$ et sa valeur est $*v_0*$ = 10,0 m·s-1.
Le graphique ci-dessous représente la trajectoire du ballon dans le repère choisi.
1. Étude du mouvement du ballon
1.1. Établir les coordonnées $*a_x*$ et $*a_y*$ du vecteur accélération du point M représentant le ballon.
1.2. Montrer que les équations horaires du mouvement du point M sont : $µ \begin{aligned} x(t) &= (v_0\cos \alpha)·t \\ y(t) &= -0,5gt^2 + (v_0\sin \alpha)·t \end{aligned} µ$
1.3. En déduire l’équation de la trajectoire du point M : $µ y(x) = \frac {-g}{2(v_0·\cos \alpha)^2} x^2+(\tan \alpha)·x µ$
1.4. Le graphique ci-dessous montre l’évolution dans le temps des grandeurs $*x*$, $*y*$, $*v_x*$, et $*v_y*$, coordonnées des vecteurs position et vitesse du point M.
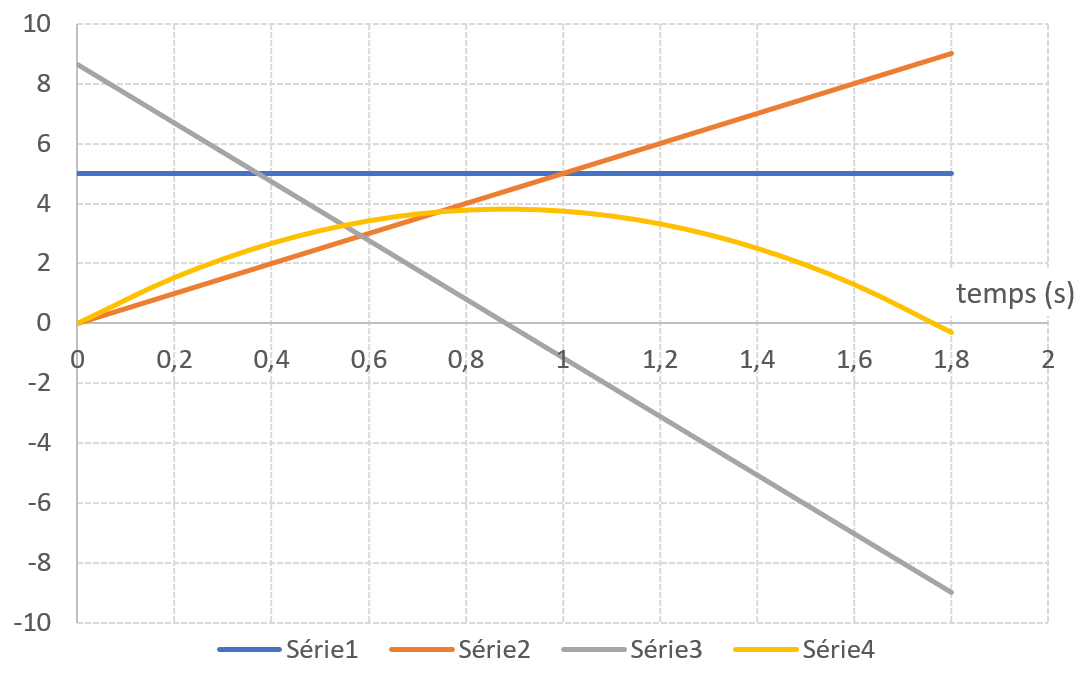
Associer à chaque courbe l’expression de la grandeur qui lui correspond et justifier.
2. Une « chandelle » réussie
2.1. Déterminer par le calcul le temps dont dispose le joueur pour récupérer le ballon avant que celui-ci ne touche le sol.
Vérifier la valeur obtenue sur l’une des courbes précédentes en expliquant votre raisonnement.
2.2. Déterminer de deux manières différentes la valeur de la vitesse $*v_1*$ du joueur pour que la chandelle soit réussie.
Correction partielle
Je vous laisse vous débrouiller avec les questions 1.1 à 1.3, les réponses étant données dans l’énoncé.
1.4. Série 1 : $*v_{0x}*$ car $*v_{0x}*$ est constant.
Série 2 : $*x*$ car $*x*$ est une fonction linéaire du temps.
Série 3 : $*v_{0y}*$ car $* v_{0y} = -gt + v_0 \sin \alpha*$ et il s’agit d’une fonction affine décroissante.
Série 4 : $*y*$ car c’est la seule grandeur qui ait l’expression d’une parabole.
D’autres justifications sont envisageables. Par exemple : la série 1 et la série 3 sont les coordonnées du vecteur vitesse car la vitesse initiale n’est pas nulle. Comme il n’y a pas d’accélération selon l’axe $*\mathrm{O}x*$, $*v_x*$ est constant et donc correspond à la série 1.
2.1. Pour ça, il faut résoudre $*y(t) = 0*$, ce qui donne $*t*$ = 1,77 s
La courbe 4, qui correspond à $*y(t)*$, vaut 0 un peu avant 1,8 S, ce qui est cohérent avec ce qu’on trouve par le calcul.
2.2 Le joueur doit avoir la même vitesse moyenne que la composante horizontale de la vitesse du ballon, soit $*v_0 \cos \alpha*$ = 5,0 m·s-1.
On peut aussi dire que le joueur dispose d’environ 1,8 s pour parcourir environ 9 m (lecture graphique de la valeur de $*x*$ à $*t*$ = 1,8 s) soit une vitesse de 9/1,8 = 5 m·s-1.
Rapport e/m de l’électron
D’après un exercice de bac – Antilles-Guyane 2013
Le physicien anglais Joseph John Thomson détermina en 1897 le rapport $*e/m*$ de l’électron. Le montage ci-dessous reprend le principe de l’expérience de Thomson. Il comporte un tube à vide dans lequel un faisceau d’électrons est dévié entre deux plaques de charges opposées. On mesure la déviation verticale du faisceau d’électrons lors de la traversée des plaques sur une longueur $*L*$, afin de déterminer la valeur du rapport $*e/m*$.
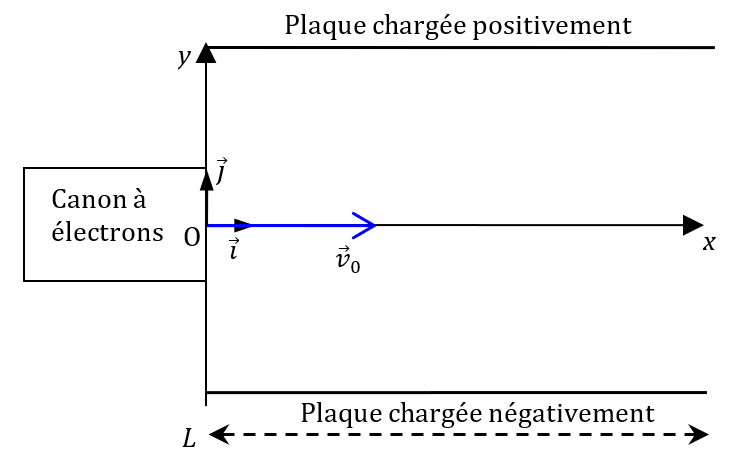
Données
- Les deux plaques forment un condensateur plan
- $*v_0*$ = 2,27·107 m·s-1
- On appelle $*h*$ la hauteur de déviation du faisceau d’électrons quand il sort des plaques.
- Intensité du champ électrostatique entre les plaques : $*E*$ = 15,0 kV·m-1.
- Longueur des plaques : $*L*$ = 8,50 cm
- Le poids des électrons est négligeable par rapport à la force électrostatique.
1. Détermination du signe de la charge de l’électron
1.1. Représenter sur le schéma le vecteur champ électrostatique $*\vec{E}*$. On prendra comme échelle 1,0 cm pour 10 kV·m-1.
1.2. J.J. Thomson a observé une déviation du faisceau d’électrons vers la plaque métallique chargée positivement. Expliquer comment J.J. Thomson en a déduit que les électrons sont chargés négativement.
1.3. Donner la relation entre la force électrostatique $*\vec{F}*$ subie par un électron, la charge élémentaire $*e*$ et le champ électrostatique $*\vec{E}*$. Montrer que le sens de déviation du faisceau d’électrons est cohérent avec le sens de $*\vec{F}*$.
2. Détermination du rapport e/m pour l’électron
2.1. Donner les coordonnées du vecteur accélération $*\vec{a}*$.
2.2. Montrer que la courbe décrite par les électrons entre les plaques a pour équation : $µ y = \frac {eE}{2mv_0^2} x^2 µ$
À la sortie des plaques, en $*x*$ = $*L*$, la déviation verticale du faisceau d’électrons par rapport à l’axe ($*\mathrm{O}x*$) a une valeur $*h*$ = 1,85 cm.
2.3. En déduire l’expression du rapport $*e/m*$ en fonction de $*E*$, $*L*$, $*h*$ et $*v_0*$ puis calculer sa valeur.
Correction
1.1. Il faut dessiner un vecteur parallèle à l’axe $*\mathrm{O}y*$ mais de sens opposé, d’une longueur de 1,5 cm.
1.2. Les charges opposées s’attirent.
1.3. $*\vec{F} = -e\vec{E} *$. $*\vec{F}*$ et $*\vec{E}*$ sont de sens opposé, donc $*\vec{F}*$ est orienté vers la plaque positive.
2.1. On a, d’après la RFD : $* m\vec{a} = -e\vec{E} *$. Or, les coordonnées de $*\vec{E}*$ sont (0, $*-E*$), donc : $µ \vec{a} \begin{pmatrix} \begin{aligned} a_x &= 0 \\ a_y &= \frac {eE}m \end{aligned} \end{pmatrix} µ$
2.2. On trouve les expressions de $*x(t)*$ et $*y(t)*$ comme d’habitude, et on exprime $*y(x)*$. Je passe les détails : $µ \begin{aligned} x &= v_0t \\ y &= \frac 12 \frac {eE}m t^2 \end{aligned} µ$
2.3. On part de : $µ h = \frac {eE}{2mv_0^2} L^2 µ$ et on isole $*e/m*$ pour trouver 1,77·1011 C·kg-1.
Tir au pigeon d’argile
Cet exercice a été donné en devoir en 2020/2021.
On étudie le mouvement d’un « pigeon » d’argile lancé pour servir de cible à un tireur.
Le pigeon d’argile de masse $*m_P*$ = 0,10 kg, assimilé à un point matériel M est lancé avec un vecteur vitesse $*\vec{v}_{\mathrm{P}0}*$ de valeur $*v_{\mathrm{P}0}*$ = 30 m·s-1, faisant un angle $*\alpha*$ = 45° avec l’horizontale.
Le tireur, situé en A, tire verticalement une balle de masse $*m_B*$ = 10 g avec un fusil de masse $*m_F*$ = 3,0 kg. La vitesse initiale de la balle est $*v_{\mathrm{B}0}*$ = 500 m·s-1. La balle, assimilée à un point matériel B part du point A tel que OA = 45 m. (Les vecteurs vitesse ne sont pas à l’échelle sur le schéma).
Le repère est constitué d’un axe $*\mathrm{O}y*$ vertical orienté vers le haut et d’un axe $*\mathrm{O}x*$ horizontal dans la direction du mouvement du pigeon. L’origine du repère est le point de départ du pigeon.
On prendra pour valeur de l’intensité du champ de pesanteur $*g*$ = 10 m·s-2.
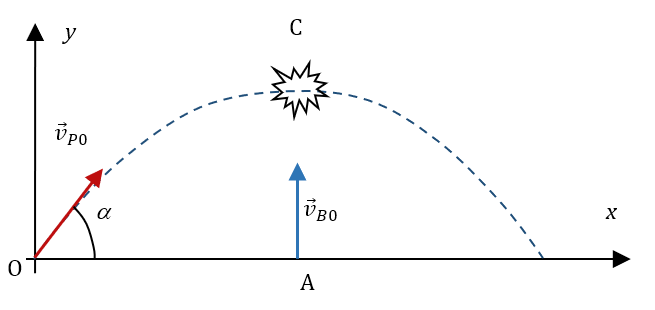
Les temps correspondants à chaque mouvement sont notés différemment : $*t*$ pour le pigeon d’argile et $*t'*$ pour la balle de fusil.
Étude du mouvement du pigeon d’argile
On notera $*t*$ le temps associé au mouvement du pigeon. À l’origine du mouvement $*t*$ = 0. On négligera les frottements s’exerçant sur le pigeon.
1. Établir les composantes $*x_P(t)*$ et $*y_P(t)*$ du vecteur $* \overrightarrow{\mathrm{OM}} *$ dans le repère (O, $*x*$, $*y*$) en fonction de $*t*$.
Tir réussi
On suppose que le tireur a réussi à toucher le pigeon d’argile.
2.1. Quelle est l’abscisse $*x_\mathrm{C}*$ du point d’impact C du pigeon d’argile et de la balle ?
2.2. Vérifier à partir de l’abscisse $*x_\mathrm{C}*$ de l’impact, que le temps de vol du pigeon d’argile est $*\Delta t*$ = 2,1 s.
2.3. Montrer que l’impact a lieu à une hauteur de 22,5 m.
On néglige toutes les forces s’exerçant sur la balle, y compris son poids.
2.4. Que peut-on dire de son accélération $*a_\mathrm{B}*$ ? Que peut-on dire de sa vitesse $*v_\mathrm{B}*$ ?
2.5. Calculer la durée $*\Delta t'*$ correspondant au temps de « vol » de la balle jusqu’à l’impact.
2.6. Comparer $*\Delta t*$ et $*\Delta t'*$ et expliquer pourquoi le tireur peut viser directement le pigeon.
Discussion sur l’effet du poids de la balle
Dans cette partie l’effet du poids de la balle n’est plus négligé mais on négligera toujours la force de frottement de l’air.
3.1. Montrer que la composante de la vitesse $*v_{\mathrm{B}y}(t')*$ dans le repère (O, $*x*$, $*y*$) vérifie l’équation : $µ v_{\mathrm{B}y}(t') = v_{\mathrm{B}0} – gt' µ$ 3.2. Calculer la vitesse $*v_{\mathrm{B}y}*$ au bout d’un temps $*\Delta t'*$ = 0,044 s, justifier pourquoi on a négligé le poids dans la partie précédente.
Correction
1. On étudie le mouvement du pigeon d’argile, dans le repère donné.
Le pigeon n’est soumis qu’à son poids, donc la RFD devient : $*\vec{P} = m\vec{a}*$ et donc $*\vec{a}=\vec{g}*$.
$µ
\begin{pmatrix} \begin{aligned}
a_x &= 0 \\
a_y &= -g
\end{aligned} \end{pmatrix}
µ$
Par intégration, on trouve les coordonnées du vecteur vitesse $*\vec{v}*$, sachant que $*v_{0x} = v_{\mathrm{P}0}·\cos \alpha*$ et $*v_{0y} = v_{\mathrm{P}0}·\sin \alpha*$.
$µ
\begin{pmatrix} \begin{aligned}
v_x &= v_{\mathrm{P}0}·\cos \alpha \\
v_y &= -gt + v_{\mathrm{P}0}·\sin \alpha
\end{aligned} \end{pmatrix}
µ$
On intègre encore une fois pour trouver les coordonnées du pigeon, sachant que $*x_{\mathrm{P}0}*$ = $*y_{\mathrm{P}0}*$ = 0.
$µ
\begin{pmatrix} \begin{aligned}
x_\mathrm{P} &= v_{\mathrm{P}0}·\cos \alpha·t \\
y_\mathrm{P} &= - \frac 12 gt^2 + v_{\mathrm{P}0}·\sin \alpha ·t
\end{aligned} \end{pmatrix}
µ$
2.1. $*x_\mathrm{C}*$ = $*x_\mathrm{A}*$ = 45 m
2.2. Temps de vol jusqu’au point C : $* \Delta t = \dfrac {x_\mathrm{C}} {v_{\mathrm{P}0}·\cos \alpha} =*$ 2,12 s
2.3. Pour cela, on calcule $*y*$ lorsque $*t*$ vaut 2,12 s et on trouve bien 22,5 m.
2.4. Si aucune force ne s’exerce sur la balle, son accélération est nulle et sa vitesse est constante.
2.5. Temps de vol de la balle : $*\Delta t'*$ = 22,5/500 = 45 ms.
2.6. $*\Delta t*$ ≫ $*\Delta t'*$ donc pendant le temps de vol de la balle, le pigeon ne se déplace que très peu. Le tireur peut donc le viser directement.
3.1. Si la balle est soumise à son poids, il apparaît une accélération de coordonnées $*a_y = -g*$ (mais $*a_x*$ = 0). Par intégration, on a $*v_{\mathrm{B}y} = -gt' + v_{\mathrm{B}0}*$.
3.2. Au bout de 44 ms, la vitesse de la balle vaut 500-10×0,044 = 499,56 m/s, donc la vitesse de la balle n’a quasiment pas changé au cours de son mouvement, ce qui explique pourquoi on a le droit de négliger le poids.
Le cyclotron
Cet exercice a été donné en devoir en 2020/2021
Nous avons vu en cours le principe de fonctionnement des accélérateurs linéaires de particules. Cet exercice a pour objectif de vous faire étudier le principe du cyclotron, qui est un autre type d’accélérateur de particules.
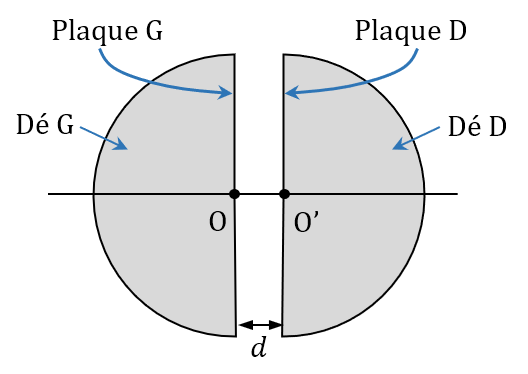
Un cyclotron est un appareil constitué de deux demi-cylindres creux appelés dés. Entre les plaques G et D règne un champ électrique $*\vec{E}*$ uniforme perpendiculaire aux plaques, d’intensité :
| $µ E = \frac Ud µ$ |
$*U*$ : la tension entre les plaques (30,0 kV) $*d*$ : la distance entre les plaques (2,00 mm) |
Dans les dés, la particule chargée est soumise à un champ magnétique d’intensité $*B*$ = 1,6 T dont le rôle est de lui communiquer un mouvement circulaire uniforme.
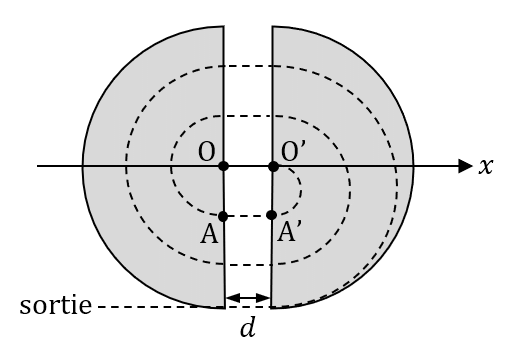
Un proton est placé sans vitesse initiale au point O à $*t*$ = 0. Il est accéléré par le champ électrique jusqu’au point O’. Dans le dé D, il a un mouvement circulaire uniforme qui l’amène au point A’. Le sens du champ électrique est alors inversé. Le proton subit une nouvelle accélération jusqu’au point A. Le processus d’accélération et de demi-tours successifs se répètent un grand nombre de fois jusqu’à ce que le proton sorte de l’accélérateur après une dizaine de microsecondes.
Données
- Masse du proton : $*m_p*$ = 1,67·10-27 kg
- Charge électrique du proton : $*e*$ = 1,60·10-19 C
- Valeur de l’électron-volt : 1 eV = 1,60·10-19 J
1. Accélération du proton
1.1. Montrer que le poids du proton est négligeable devant la force électrique $*\vec{F}*$ qu’il subit.
1.2. Indiquer la direction et le sens de $*\vec{E}*$ et $*\vec{F}*$.
1.3. Établir l’expression de l’accélération $*\vec{a}*$ entre O et O’.
1.4. Montrer que l’abscisse $*x*$ du proton sur son trajet OO’ est donnée par la relation : $µ x(t) = \frac{eU}{2m_p d} t^2 µ$
1.5. En déduire la durée $*\Delta t_1*$ mise par le proton pour aller de O à O’.
2. Mouvement du proton dans les dés
2.1. Entre O’ et A’, le proton a un mouvement circulaire uniforme. En déduire la relation entre sa vitesse $*v*$, le rayon $*R*$ de la trajectoire et la durée $*\Delta t_2*$ de ce demi-tour.
Le rayon $*R*$ de la trajectoire d’un proton dans un dé est donnée par la relation : $µ R = \frac{m_p v}{eB} µ$
2.2. En déduire que la durée $*\Delta t_2*$ peut s’exprimer sous la forme : $µ \Delta t_2 = \frac{\pi m_p}{eB}µ$
2.3. Que peut-on dire de la durée des demi-tours suivants ?
3. Énergie cinétique du proton
La variation d’énergie cinétique du proton est égale au travail $*W*$ de la force électrique.
3. Évaluer le nombre de tours que doit faire le proton pour qu’il atteigne, à la sortie du cyclotron, une énergie de 16 MeV.
Correction
1.1. $*P=mg=*$ 1,67·10-27×9,8 = 1,6·10-26 N et $*F = qE=*$ 2,40·10-12 N
donc $*F*$ est 1,5·1014 fois plus grande que $*P*$. Le poids est bien négligeable.
1.2. Pour que le proton accélère de O vers O’, il faut que $*\vec{F}*$ et donc $*\vec{E}*$ aient pour direction la droite OO’ et pour sens de O vers O’.
1.3. Comme $*\vec{F}*$ est la seule force non négligeable qui s’exerce sur le proton, on a, d’après la RFD, $*\vec{F}=m\vec{a}*$ donc $µ \vec{a}= \dfrac {eE}{m_p} \vec{i} µ$ avec $*\vec{i}*$ vecteur unitaire ayant même direction et même sens que $* \vec{E} *$.
1.4. Pour trouver le vecteur vitesse, on intègre $*\vec{a}*$ en tenant compte du fait que $*\vec{v}_0*$ est nulle.
$µ \vec{v} = \frac {eE}{m_p} t·\vec{i} µ$
Puis, pour trouver le vecteur positon $* \overrightarrow{\mathrm{OM}} *$, on intègre $*\vec{v}*$ en tenant compte qu’à $*t*$ = 0, le proton est à l’origine du repère.
$µ \overrightarrow {\mathrm{OM}}= \frac {eE}{2m_p} t^2·\vec{i} µ$
Comme $* E= \dfrac Ud *$ on obtient au final :
$µ x(t) = \frac{eU}{2m_p d}·t^2 µ$
1.5. On cherche $*t*$ pour que $*x=d*$ : $* t = \sqrt{\dfrac{2m_p d^2}{eU}} = *$ 1,67 ns. Donc $*\Delta t_1*$ = 1,67 ns.
2.1. Le proton parcourt un demi-cercle de rayon $*R*$ soit une distance $*\pi R*$ à une vitesse $*v*$, donc $*\Delta t_2 = \dfrac{\pi R}v *$
2.2. Il suffit de remplacer $*R*$ par l’expression donnée et de simplifier par $*v*$.
2.3. On voit que l’expression de $*\Delta t_2*$ ne dépend pas de la vitesse du proton, donc la durée des demi-tours suivants est toujours la même.
3. À chaque passage entre les plaques, le travail de la force électrique vaut $*W=Fd=*$ 4,80·10-15 J soit 30 keV. Donc pour atteindre 16 MeV, il faut 16000÷30 = 533 passages, soit 533÷2 = 267 tours.