P5. Transferts thermiques
Ce chapitre est la suite logique du chapitre précédent. On va s’intéresser à l’aspect dynamique des échanges thermiques.
Modes de transferts thermiques
- Caractériser qualitativement les trois modes de transfert thermique : conduction, convection, rayonnement.
Il y a trois manières d’échanger de l’énergie thermique. Par conduction, par convection et par rayonnement.
Plus c’est chaud, plus ça bouge !
Conduction
Le transfert thermique par conduction a lieu essentiellement dans un solide. Les vibrations des particules « chaudes » du solide se transmettent de proche en proche.
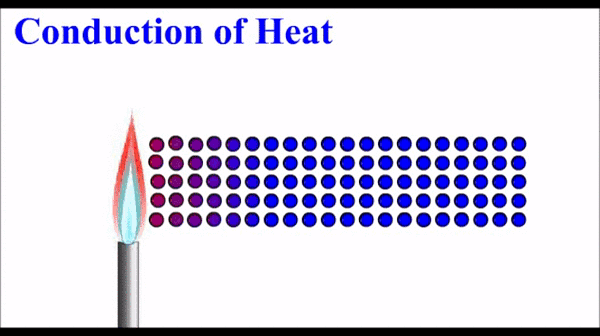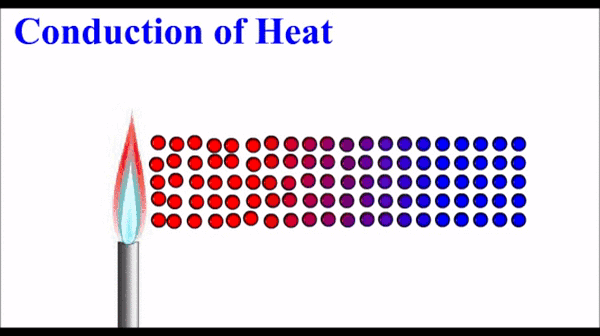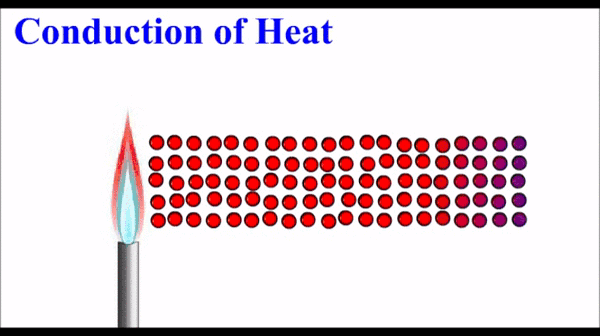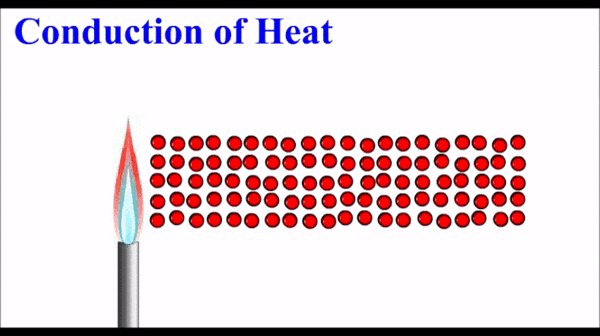
Certains solides sont meilleurs conducteurs de chaleur que d’autres. Nous y reviendrons… 😊
Convection
La conduction par convection ne se produit que dans un fluide. La convection implique des mouvements du fluide dus aux différences de densité entre les parties chaudes et les parties froides du fluide.
Par exemple, lorsque vous chauffez de l’eau dans une casserole (la source de chaleur est en-dessous de la casserole, donc… 😊), la température de l’eau du fond s’élève, celle-ci devient moins dense et remonte à la surface, alors que l’eau froide à la surface de la casserole plonge vers le fond. Ces mouvements de convection contribue à conduire l’énergie thermique dans toute l’eau.
Rayonnement
Vous l’avez déjà vu plusieurs fois au cours de votre scolarité, tout corps qui n’est pas au « zéro absolu » émet un rayonnement dont les caractéristiques dépendent de sa température. Ce rayonnement peut transmettre de l’énergie thermique s’il est absorbé par un autre corps.
C’est le seul mode de transfert qui puisse se faire dans le vide.
Vous avez tous fait l’expérience, je présume, de vous trouvez à proximité d’un feu. Et vous avez tous senti la « chaleur » du feu sur votre visage. Cette sensation n’est pas due à l’air qui serait chaud mais au rayonnement (infrarouge) émis par le feu. En effet, la peau du visage est plus sensible au rayonnement infrarouge que d’autres parties du corps.
Coexistence des modes de transfert
Ces trois modes de transferts ne sont pas exclusifs les uns des autres. Ainsi, lorsque vous posez une casserole pleine d’eau sur une plaque vitrocéramique allumée, l’énergie thermique cédée par la plaque à la casserole se fait aussi bien par rayonnement que par conduction.
De même, dans un liquide très visqueux (le miel par exemple, ou le magma), la conduction peut jouer un rôle aussi important, voire plus, que la convexion.
La seule chose dont vous pouvez être sûr, c’est que la convection ne peut pas se faire dans un solide, et que conduction et convexion nécessitent de la matière
Flux et résistance thermiques
- Exploiter la relation entre flux thermique, résistance thermique et écart de température, l’expression de la résistance thermique étant donnée.
Flux thermique
Rien de bien complexe à comprendre dans la notion de « flux thermique », il s’agit d’une puissance (en W, donc…) thermique. Autrement dit d’un nombre de joules échangés chaque seconde sous forme d’énergie thermique.
L’usage veut que l’on note $*\Phi*$ (phi majuscule) le flux thermique, plutôt que $*P*$, et $*Q*$ l’énergie thermique échangée, plutôt que $*E*$. Mais bon, ce n’est pas gravé dans le marbre non plus, et $*P_{th}*$ ou $*E_{th}*$, ça va bien aussi. 😊
Dans tous les cas, la formule $*E = P·\Delta t*$ est toujours valable, bien entendu. Sauf qu’elle s’écrit $*Q = \Phi·\Delta t*$.
| $µ Q = \Phi·\Delta t µ$ | $*Q*$ : chaleur / énergie thermique (J) $*\Phi*$ : flux thermique (W) $*\Delta t*$ : durée du transfert (s) |
Mais (parce qu’il y a un « mais » 😊), cette formule n’est valable que si le flux $*\Phi*$ est constant. C’est le même principe que la formule vue au collège : $*d = v·t*$. Si la vitesse n’est pas constante, on ne peut pas l’utiliser.
Si le flux varie, il faut raisonner pendant un tout petit instant $*\delta t*$, durant lequel on peut considèrer que $* \Phi *$ est constant. L’énergie thermique échangée est toute petite et se note alors $*\delta Q*$. Du coup, la relation $* Q = \Phi·\Delta t *$ devient $* \delta Q = \Phi·\delta t *$. Le flux peut donc s’écrire : $µ \Phi = \frac {\delta Q}{\delta t} µ$
Et pour être vraiment juste, il faut faire tendre $*\delta t*$ vers 0. Et donc le rapport $* \frac {\delta Q}{\delta t} *$ devient la dérivée de $*Q*$ par rapport au temps.
| $µ \Phi = \frac{\mathrm{d}Q}{\mathrm{d}t} µ$ | $*Q*$ : chaleur / énergie thermique (J) $*\Phi*$ : flux thermique (W) $*\Delta t*$ : durée du transfert (s) |
Résistance thermique
La résistance thermique $*R_{th}*$ d’une surface mesure sa capacité à ralentir l’échange thermique (c’est-à-dire le flux thermique) entre les deux côtés.
Le flux thermique $*\Phi*$ est proportionnel à l’écart de température entre les deux côtés séparés par la surface.
| $µ \Phi = \frac {\Delta T}{R_{th}} µ$ | $*R_{th}*$ : Résistance thermique (K·W-1) $*\Phi*$ : flux thermique (W) $*\Delta T*$ : différence de température (K) |
Attention : le flux est une grandeur algébrique. Son signe dépend du système auquel on s’intéresse. S’il perd de la chaleur, $*\Phi*$ est négatif et inversement. Donc l’expression de $*\Delta T*$ ($*T_{froid} - T_{chaud}*$ ou $*T_{chaud} - T_{froid}*$) dépend aussi du système auquel on s’intéresse et doit être choisi pour tenir compte du sens de l’échange de chaleur.
$*U*$ est une différence de potentiel provoquant un flux de charge $*I*$ de même que $*\Delta T*$ est une différence de température créant un flux d’énergie thermique $* \Phi *$.
Ce flux est modulé par la résistance thermique $*R_{th}*$.
La résistance thermique d’une paroi dépend bien sûr du matériau dont elle est constitué. Le bois, par exemple, possède une conductivité thermique (notée $*\lambda*$) plus faible que le béton. Mais ce n’est pas le seul facteur ayant une influence sur la résistance thermique d’une paroi. Il y a sa surface $*S*$ (plus une surface est grande, mieux elle permet les échanges thermiques) et aussi son épaisseur $*e*$ (plus la paroi est épaisse, plus sa résistance thermique est grande).
Pour calculer la résistance thermique d’une paroi, il faut utiliser la formule :
| $µ R_{th} = \frac e{\lambda ·S} µ$ | $*R_{th}*$ : Résistance thermique (K·W-1) $*e*$ : épaisseur $*\lambda*$ : conductivité thermique du matériau (W·m-1·K-1) $*S*$ : surface de la paroi |
Cette formule n’est pas à connaître par cœur, mais vous devez savoir vous en servir…
Flux thermique à travers une fenêtre
Soit une fenêtre de dimensions 1,00 m × 1,20 m et d’épaisseur 5 mm.
La conductivité thermique du verre vaut $*\lambda*$ = 1,15 W·m-1·K-1.
1. Calculer le flux thermique traversant cette fenêtre en considérant une température intérieure de 20 °C et une température extérieure de 0 °C.
On considère maintenant une fenêtre en double vitrage de même dimension, constitué de deux plaques de verre de 2,5 mm séparées par 5 mm d’air. $*\lambda_{air}*$ = 0,025 W·m-1·K-1.
2. Calculer le flux thermique $*\Phi*$ traversant cette fenêtre dans les mêmes conditions que pour la question 1, on négligera le phénomène de convection de l’air entre les deux plaques de verres. Commenter.
Correction
1. $*R_{th}*$ = 3,62·10-3 K·W-1
$*\Phi*$ = 5,52 kW
2. On ajoute la résistance thermique des deux couches de verre et de la couche d’air : $*R_{th}*$ = 2×1,81·10-3 + 0,167 = 0,17 K·W-1
$*\Phi*$ = 117 W
Un fenêtre à double vitrage est un isolant bien plus efficace qu’une fenêtre simple.
Température d’un système
- Effectuer un bilan d’énergie pour un système incompressible échangeant de l’énergie par un transfert thermique modélisé à l’aide de la loi de Newton fournie. Établir l’expression de la température du système en fonction du temps.
- Capacité mathématique : résoudre une équation différentielle linéaire du premier ordre à coefficients constants avec un second membre constant.
On a vu au chapitre précédent la relation entre l’énergie interne $*U*$ d’un système incompressible (un solide ou un liquide) et sa température. Vous savez maintenant également calculer le flux thermique entre un corps chaud et un corps froid dans certaines conditions.
Mais comment évolue la température d’un système au cours du temps ?
TP Refroidissement
- Suivre et modéliser l’évolution de la température d’un système incompressible.
Objectif : suivre et modéliser l’évolution de la température d’un volume d’eau chaude contenu dans un récipient et exposé à l’air tempéré de la salle de TP.
Travail demandé
- Suivre l’évolution de la température d’environ 150 mL d’eau chaude (température initiale 80 à 85 °C) pendant une vingtaine de minutes. Vous placerez cette eau dans un bécher avec une agitation modérée. Relevez sa température toutes les 30 secondes environ.
- Importez vos valeurs dans Regressi (un tableur n’est pas capable de modéliser la fonction $*\theta(t)*$ obtenue)
- Tracer le graphique $*\theta(t)*$ et modéliser cette fonction.
- Vérifier que cette évolution est compatible avec la loi de refroidissement de Newton (voir plus bas).
Le problème qui se pose
De manière générale, le flux thermique $*\Phi*$ entre un corps à la température $*T*$ et le milieu environnant à la température $*T_{ext}*$ est proportionnel à la différence de température entre le corps et le milieu environnant. De sorte qu’on peut écrire : $*\Phi = k·(T_{ext}-T)*$ ($*\Phi*$ < 0 si le système perd de la chaleur).
Comme vous l’aurez certainement noté, le flux dépend de l’écart de température entre le système et l’extérieur et réciproquement ! Plus le flux est important, plus la température du corps se rapproche rapidement de la température extérieure. Et plus sa température est proche de la température extérieure, moins le flux est important. Donc plus le flux est important, plus vite il diminue… 😅
Prenons un exemple pour fixer les idées. Imaginons 1 L d’eau à 60 °C dans un récipient, placé dans une pièce où il fait 20 °C. La température de la pièce ne varie pas au cours de l’expérience (on dit que le milieu est « thermostaté »). Supposons que la résistance thermique $*R_{th}*$ de la bouteille vale 0,1 K·W-1.
Alors, le flux initial vaut $*\Phi = \cfrac {T_{ext}-T}{R_{th}} *$ = –40÷0,1 = –400 W.
Donc au bout d’une seconde, l’énergie interne $*U*$ de l’eau a diminué de 400 J. Ce qui entraîne une baisse de sa température. Calculons-là !
La baisse d’énergie interne de 400 J permet d’écrire : $*m·c_{\text{eau}}·(T_f-60) = -400*$.
$*m*$ = 1 kg, $*c_{\text{eau}}*$ = 4,2 kJ·kg-1·K-1.
Un petit calcul nous amène à $*T_f*$ = 59,9 °C.
Du coup, $*\Phi*$ n’a plus sa valeur de tout à l’heure car la différence de température entre l’eau et la pièce ne vaut plus 40 °C mais 39,9 °C. 😊
Alors on pourrait faire plein de calculs avec Python ou un tableur pour suivre la température au cours d’intervalle de temps très petit. On l’a déjà fait, ça s’appelle la méthode d’Euler et on l’a vu au cours du TP Mouvement elliptique du chapitre P3. Mais n’abusons pas des bonnes choses. 😆
Établissement de l’équation différentielle
On va regrouper les deux équations régissant l’évolution de la température en une seule. On note $*T*$ la température de l’eau à un instant $*t*$, $*T_{ext}*$ la température du milieu extérieur (supposée constante) et $*T_i*$ la température initiale de l’eau.
On a d’une part :
équation qui régit la perte de chaleur de l’eau, et d’autre part :
équation qui lie l’énergie perdue et la variation de température, qu’on a vue au chapitre précédent.
Maintenant, il ne nous reste plus qu’à réunir les équations (1) et (2) et on obtient : $µ \frac{\mathrm{d}}{\mathrm{d}t}(m·c_{\text{eau}}·(T - T_i)) = \cfrac{T_{ext} - T}{R_{th}} µ$ Quand on dérive $*m·c_{\text{eau}}·(T - T_i)*$ par rapport au temps, puisqu’il n’y a qu’une seule fonction de temps ici, qui est $*T*$ et que je devrais noter $*T(t)*$ mais ça alourdit l’écriture, on obtient : $µ \frac{\mathrm{d}}{\mathrm{d}t}(m·c_{\text{eau}}·(T - T_i)) = m·c_{\text{eau}}·\frac{\mathrm{d}T}{\mathrm{d}t} µ$ du coup, on obtient :
Voici l’équation différentielle ! 🤗 $*T*$ est une fonction du temps inconnue qui vérifie l’équation (3).
Pour les méthodes de résolution d’équations différentielles, voir dans la rubrique Divers.
Pour résoudre cette équation différentielle, il faut d’abord la réécrire sous une forme qui va faciliter sa résolution : $µ \cfrac {\mathrm{d} T}{\mathrm{d} t} + aT = b µ$ avec $*a = \dfrac 1{R_{th}·m·c_{\text{eau}}}*$ et $*b = \dfrac{T_{ext}}{R_{th}·m·c_{\text{eau}}}*$
Après résolution et simplification, on trouve :
Il ne nous reste plus qu’à trouver $*K*$ en tenant compte du fait que $*T(0)*$ = 60 °C, soit $*K*$ = 40 °C.
Le graphique ci-dessous montre l’évolution de la température de l’eau dans les conditions du problème. On voit bien qu’au début, à cause d’une différence de température $*\Delta_e T*$ élevée, le refroidissement est rapide. Puis l’eau se refroidit de plus en plus lentement jusqu’à ce que sa température atteigne la température de la pièce.
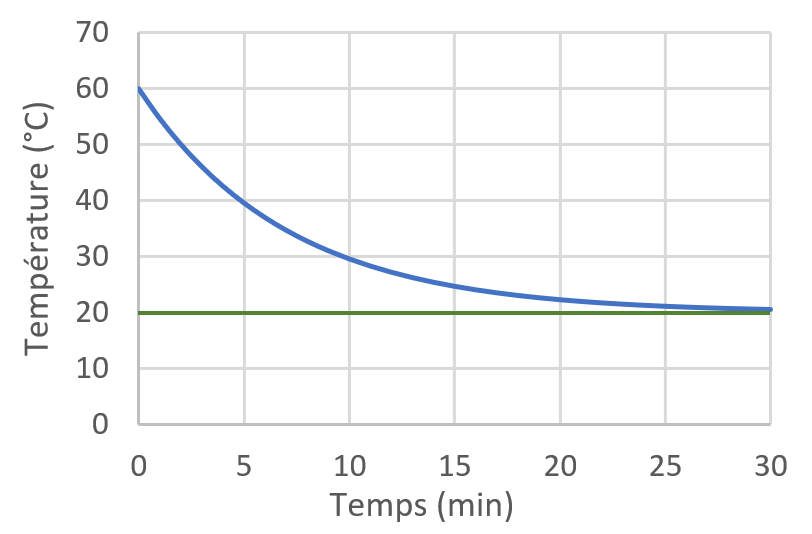
Bien sûr, il n’est pas question de détailler autant que dans ce cours. Vous pouvez faire beaucoup plus condensé. Voici comment établir rigoureusement mais brièvement l’expression de la température $*T*$ d’un système en contact avec un milieu thermostaté de température $*T_{ext}*$.
- $*\Phi = \dfrac {\mathrm{d}Q}{\mathrm{d}t} = k·(T_{ext} - T)*$ ($*\phi*$ < 0 si le système est plus chaud que l’extérieur)
- $*Q = C·(T - T_i)*$ ($*C*$ : capacité thermique du système)
- Donc : $* \dfrac {\mathrm{d}}{\mathrm{d}t}(C·(T - T_i)) = k·(T_{ext} - T) *$
- Après calcul de la dérivé : $* C\dfrac {\mathrm{d}T}{\mathrm{d}t} = k·(T_{ext} - T)*$
- On réorganise l’équation différentielle : $* \dfrac {\mathrm{d}T}{\mathrm{d}t} + \dfrac kC·T = \dfrac {k·T_{ext}}C *$
- La solution de cette équation différentielle est : $* T = K·e^{-\frac kC t} + T_{ext} *$
- En tenant compte du fait qu’à $*t*$ = 0, $*T*$ = $*T_i*$, on trouve que $*K*$ = $*T_i - T_{ext}*$
Loi de refroidissement de Newton
Ce que je vous disais plus haut à propos de flux thermique qui est proportionnel à la différence de température entre un milieu chaud et un milieu froid est appelée la loi de refroidissement de Newton. Je cite Wikipédia :
« La loi de refroidissement de Newton, énoncée par Isaac Newton stipule que le taux de perte de chaleur d’un corps est proportionnel à la différence de température entre le corps et le milieu environnant. Cette formulation n’est pas très précise, et présuppose un milieu et un corps homogènes ainsi qu’un milieu à température constante. »
Nous avons déjà vu un cas particulier de cette loi avec l’expression $*\Phi = \frac {\Delta T}{R_{th}}*$ pour un flux à travers une paroi. Dans ce cas, le facteur de proportionnalité vaut $* \frac 1{R_{th}}*$. Mais tous les échanges de chaleur ne se ramène pas forcément à cette situation (par exemple, un objet solide placé dans un milieu de température différente).
Cette loi pourra être mentionnée dans un exercice, mais elle sera toujours rappelée.
Résistance thermique d’un thermos
On souhaite évaluer la résistance thermique d’un thermos d’une contenance de 0,60 L.
Pour cela, on le remplit d’eau chaude puis on suit l’évolution de la température de cette eau pendant un certain temps, dans une pièce à 23 °C.
On obtient les mesures suivantes :
| $*t*$ (min) | $*\theta*$ (°C) | $*t*$ (min) | $*\theta*$ (°C) |
|---|---|---|---|
| 0 | 77,9 | 70 | 54,6 |
| 10 | 73,6 | 80 | 51,9 |
| 20 | 69,7 | 90 | 49,7 |
| 30 | 66,3 | 100 | 48,0 |
| 40 | 62,8 | 110 | 45,8 |
| 50 | 60,1 | 120 | 43,9 |
| 60 | 57,3 | 130 | 42,8 |
À l’aide d’un tableur, en déduire la résistance thermique du thermos.
Correction
On sait que l’expression de la température en fonction du temps est $*T = (T_0 - T_{ext})e^{-\frac kC t} + T_{ext}*$. Dans le cas d’un système contenu dans une enveloppe de résistance thermique $*R_{th}*$, on sait que $*k = \frac 1{R_{th}}*$.
L’idée est de modéliser, grâce au tableur, la température $*\theta*$ en fonction du temps, puis, à partir de l’expression de ce modèle, de trouver $*R_{th}*$.
Attention : Excel n’est pas capable de modéliser des expressions de la forme $*Ae^{-kt} + B*$ mais seulement de la forme $*Ae^{-kt}*$. Donc il ne faut pas tracer $*\theta (t)*$ mais $*\theta (t) - 23 = f(t)*$, de manière à modéliser l’expression $*(T_0 - T_{ext})e^{-\frac 1{R_{th}C} t}*$
On commence donc par tracer le graphique et modéliser $*\theta (t) -23*$. N’oubliez pas de convertir le temps en seconde.
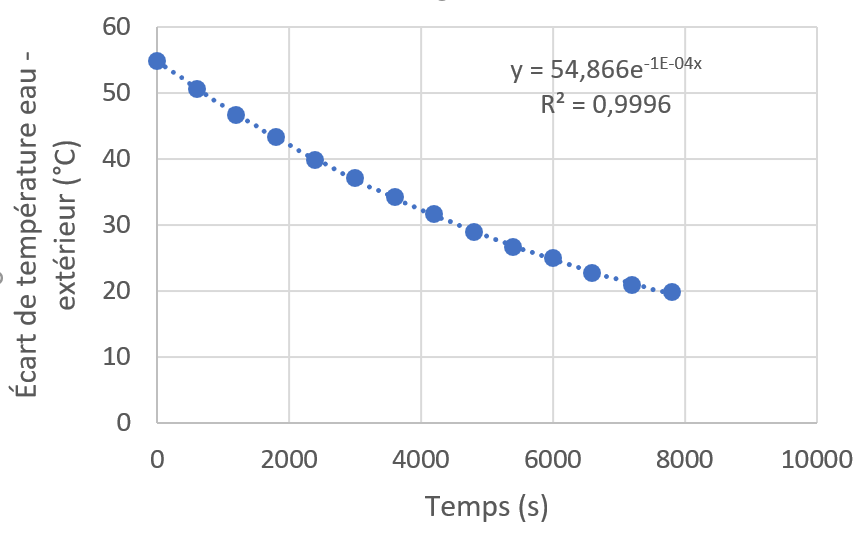
On obtient donc que $*\frac 1{R_{th}C} *$ = 10-4 s-1 (il faut croire qu’Excel arrondit fortement cette valeur…)
On calcule $*C*$ : $*C = m·c_{eau} = *$ 0,60×4,2·103 = 2,52·103 J·K-1.
On peut donc en déduire $*R_{th} =*$ 4,0 K·W-1.
Remarque
On arrive dans les limites d’Excel du point de vue de ses capacités de modélisation. Il vaut mieux ici utiliser Regressi qui non seulement est capable de chercher un modèle de type $*T = (T_0 - T_{ext})e^{-\frac 1{R_{th}C} t} + T_{ext}*$, mais en plus donne $*\frac 1{R_{th}C}*$ = 1,3·10-4 s-1, ce qui permet de calculer plus précisément la valeur de $*R_{th}*$. Avec Regressi, on trouve une résistance thermique de 3,1 K·W-1 ce qui est plus conforme à la valeur attendue.
Climat de la Terre et effet de serre
- Effectuer un bilan quantitatif d’énergie pour estimer la température terrestre moyenne, la loi de Stefan-Boltzmann étant donnée.
- Discuter qualitativement de l’influence de l’albédo et de l’effet de serre sur la température terrestre moyenne.
Cette partie n’est pas au programme des épreuves écrites de mars 2022.
Révision & entraînement
Durée de vie d’une sonde vénusienne
La température au sol sur Vénus est de l’ordre de 470 °C. À cause de cela, une sonde qui se pose à la surface de Vénus a une durée de vie très brève, car rapidement sa température interne devient trop grande pour le bon fonctionnement de ses circuits électroniques.
On se propose, dans cet exercice, d’estimer la durée de vie d’une sonde en en faisant un modèle simple.
La sonde est modélisée par une sphère de 60 cm de rayon, enveloppée par un isolant thermique d’épaisseur $*e*$ = 5,0 cm et de conductivité thermique $*\lambda*$ = 0,06 W·m-1·K-1. On supposera que la température est homogène à l’intérieur de la sonde.
La capacité thermique de la sonde est comparable à celle de 30 L d’eau ($*c_{eau}*$ = 4,2·103 J·K-1·kg-1).
Au moment de se poser sur Vénus, sa température interne est déjà de 70 °C
La température limite de fonctionnement des circuits électroniques est de 125 °C.
1. Calculer la résistance thermique des parois de la sonde.
2. Établir l’expression de la température du système en fonction du temps.
3. En déduire la durée de vie de la sonde à la surface de Vénus.
Correction
1. $*R_{th} = \dfrac{e}{\lambda·S} = \dfrac{5·10^{-2}}{0,06×4 \pi 0,6^2} *$ = 0,184 K·W-1.
2. On établit l’équation différentiel en utilisant la relation entre le flux et la quantité de chaleur échangée :
$µ \Phi = \frac Q{\Delta t} = \frac {mc\Delta T}{\Delta t} \tag {1}µ$
et la relation entre le flux et la différence de température intérieur-extérieur :
$µ \Phi = \frac {T_{ext}-T}{R_{th}} \tag {2} µ$
On obtient l’équation différentielle : $* mc \dfrac {\mathrm{d}T}{\mathrm{d} t} = \dfrac {T_{ext}-T}{R_{th}} *$
On réarrange l’équation pour se ramener à la forme connue $*f’ + af = b*$ :
$µ \dfrac {\mathrm{d}T}{\mathrm{d} t} + \dfrac {T}{mcR_{th}} = \dfrac {T_{ext}}{mcR_{th}} µ$
La solution est $*T = Ke^{-at} + T_{ext}*$
avec $*a = \dfrac {1}{mcR_{th}} = \dfrac {1}{30×4,2·10^3×0,184} =*$ 4,31·10-5 s-1 et $*K*$ = –400 °C
3. On peut tracer une courbe ou résoudre l’équation $*125 = -400·e^{-4,31·10^{-5}t} + 470*$.
Mais si vous n’avez pas encore fait les logarithmes et les exponentielles, ça va être dur… 😏
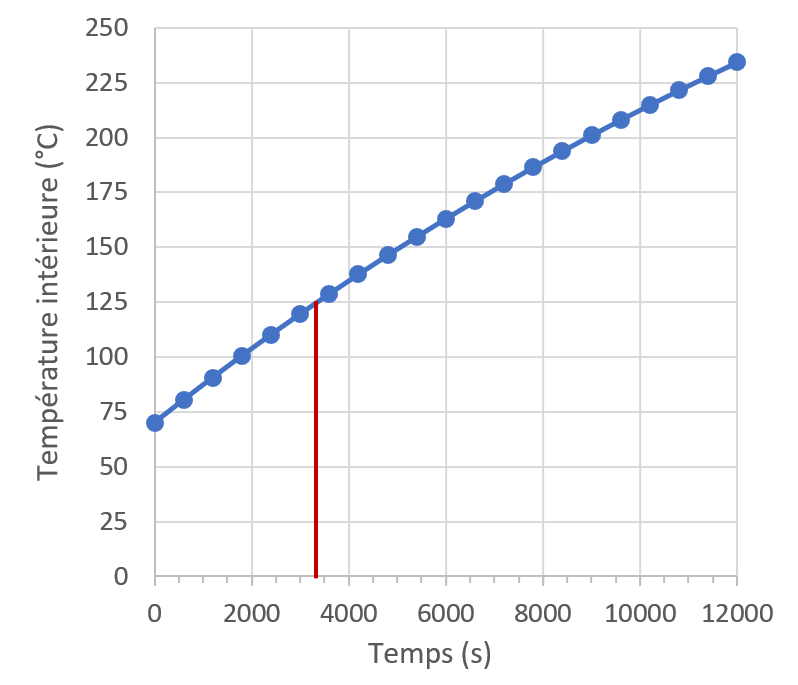
On trouve autour de 3400 s, soit environ 57 minutes.
Chauffe-eau électrique
Cet exercice a été donné en devoir en 2020/2021.
On s’intéresse dans cet exercice à un chauffe-eau électrique d’une capacité de 120 L. Un chauffe-eau est simplement un récipient isolé thermiquement, avec une arrivée d’eau froide et une sortie d’eau chaude. Cette eau est chauffée par une résistance électrique qui est parcourue par un courant électrique jusqu’à ce que l’eau arrive à la température souhaitée. On considère dans cet exercice que cette température est de 60 °C.
Données
- capacité calorifique massique de l’eau $*c_{eau}*$ = 4,18 kJ·K-1·kg-1
- 1 bar = 105 Pa
- 0 K = –273 °C
- Constante des gaz parfaits $*R*$ = 8,314 J·mol-1·K-1
- Le flux thermique à travers une paroi de surface $*S*$ et de résistance thermique $*R_{th}*$ séparant deux milieux de température $*T_1*$ et $*T_2*$ s’écrit : $µ |ϕ|= {|T_1-T_2 | \over R_{th}} µ$
Quelques considérations préliminaires
1. Qu’est-ce qui différencie, à l’échelle des molécules, de l’eau à 20 °C et de l’eau à 60 °C ?
2. Dans quel sens s’effectue le transfert thermique entre la résistance électrique et l’eau du chauffe-eau lorsque la résistance est traversée par un courant ?
3. Citer les trois modes de transfert thermique que vous connaissez. Indiquer lequel joue un rôle prépondérant dans la situation qui nous intéresse et justifier votre réponse en caractérisant ce mode de transfert thermique.
4. L’eau contenue dans le chauffe-eau possède une énergie interne $*U*$. Expliquer pourquoi il est quasi-impossible de déterminer la valeur de $*U*$ en citant notamment quelques composantes de cette énergie interne.
Bilan énergétique dans la phase de chauffage
Dans cette question, on se place dans la situation où le chauffe-eau est rempli d’eau et que la température de cette eau est de 30 °C. Le chauffe-eau est donc toujours en train de chauffer l’eau.
5.1. Faire un bilan énergétique de la situation à l’aide d’un schéma où vous ferez figurez le chauffe-eau et les différentes énergies reçues ou cédées par celui-ci.
5.2. L’énergie reçue par le chauffe-eau est-elle égale à l’énergie perdue ? Justifier votre réponse.
On fait l’approximation que la puissance du transfert thermique entre le chauffe-eau et l’extérieure est négligeable devant la puissance du transfert thermique entre la résistance chauffante et l’eau. On reviendra plus tard sur la pertinence de cette approximation. La puissance thermique transféré par la résistance vaut $*P_J*$ = 3000 W. La température initale de l’eau est de 14 °C.
6. Combien de temps faut-il pour chauffer les 120 L d’eau à 60 °C ?
Maintien de l’eau chaude à température
Le chauffe-eau est entouré d’une couche de $*e*$ = 3 cm d’isolant thermique dont la conductivité thermique vaut $*\lambda*$ = 0,045 W·m-1·K-1. Il a la forme d’un cylindre de hauteur 80 cm et de rayon 25 cm.
7.1. À l’aide de la relation $*R_{th} = \frac e{\lambda S}*$ , $*S*$ étant la surface d’échange entre le chauffe-eau et l’extérieur, c’est-à-dire la surface du cylindre, calculer la résistance thermique $*R_{th}*$ du chauffe-eau.
7.2. Quelle doit être la puissance de veille du chauffe-eau, c’est-à-dire la puissance nécessaire au maintien de l’eau à 60 °C ? On considère que la température dans la pièce où se trouve le chauffe-eau est de 20 °C.
7.3. L’approximation faite juste avant la question 6 est-elle pertinente ? Expliquer brièvement.
C’est déjà les vacances ? 😃
Les habitants de l’appartement partent en vacances. Comme ils ont une conscience écologique, ils coupent le chauffe-eau avant de partir. Celui-ci était initialement plein d’eau à 60 °C.
8.1. Établir l’expression de l’équation différentielle régissant l’évolution de la température $* \theta *$ de l’eau dans le chauffe-eau en fonction du temps. On considère que la température dans la salle de bain est constante et vaut toujours 20 °C.
8.2. Montrer que la solution de cette équation différentielle est $µ θ(t)=θ_0·e^{\frac{-t}{\tau}}+ θ_1 µ$ avec $* \tau = R_{th}mc_{eau} *$. Précisez les valeurs de $*θ_0*$ et $*θ_1*$.
8.3. Quelle sera la température de l’eau après 48 h ? Et après leur retour de vacances au bout de 15 jours ?
Quand ça marche pas bien…
Un dysfonctionnement du système a créé l’apparition d’une « poche » d’air à l’intérieur du chauffe-eau. Cette poche d’air a un volume de 1 L. Au retour des vacances des occupants, on considère que l’eau à l’intérieur du chauffe-eau a une température de 20 °C. L’air a donc la même température et une pression de 1 bar.
Les occupants mettent le chauffe-eau en marche. Ceci a pour effet de chauffer l’air contenu dans le chauffe-eau, mais, celui-ci étant « emprisonné » son volume ne change pas. Un dispositif de sécurité coupe le chauffe-eau si la pression à l’intérieur dépasse 2 bar.
9. Le chauffe-eau va-t-il pouvoir chauffer l’eau jusqu’à 60 °C ? Justifier votre réponse par un calcul.
10. On a supposé ici que l’air se comportait comme un gaz parfait. Que suppose ce modèle ? Proposer une situation où ce modèle ne serait pas adapté.
Correction
1. Dans l’eau à 60 °C, les molécules d’eau sont plus agitées.
2. Toujours du chaud vers le froid, donc de la résistance vers l’eau.
3. Conduction, convection, rayonnement. Ici, c’est la convection qui joue un rôle prépondérant. La convection implique des mouvements du fluide dus aux différences de densité entre les parties chaudes et les parties froides du fluide.
4. L’énergie interne est composée des énergies cinétiques microscopiques des particules, plus les énergies potentielles microscopiques dues aux interactions entre les molécules, ions, atomes, électrons, noyaux, nucléons…
5.a. Bilan énergétique sous forme de schéma

5.b. Non car l’énergie interne du chauffe-eau augmente. Il y a accumulation d’énergie sous forme d’énergie thermique de l’eau.
6. Énergie nécessaire : $*Q*$ = 120×4,18·103×46 = 23,1 MJ
Donc $*Δt = \dfrac QP =*$ 7,7·103 s soit environ 2h et 8 minutes
7.1. Surface du cylindre : $*S*$ = π×0,252×2 + 2π×0,25×0,8 = 1,65 m2
Donc $*R_{th} = \dfrac e{\lambda S} =*$ 0,03÷(0,045×1,65) = 0,404 K·W-1
7.2. Calcul du flux thermique sortant du chauffe-eau : $*\Phi*$ = 40÷0,404 = 99 W.
7.3. La puissance pour maintenir l’eau chaude (99 W) est beaucoup plus petite que la puissance pour chauffer (3000 W).
8.1. Le flux thermique dépend de la différence de température entre l’intérieur et l’extérieur :
$µ \phi =\frac {T_{ext}-T}{R_{th}} µ$
Le flux thermique est également la dérivée de la quantité de chaleur échangée $*Q*$ :
$µ ϕ = \frac {\mathrm{d}Q}{\mathrm{d}t}µ$
Or
$µ Q = mc(T(t) - T_i) µ$
où $*T_i*$ est la température initiale de l’eau et $*T(t)*$ sa température à l’instant $*t*$. Donc
$µ ϕ=mc\dfrac{\mathrm{d}T}{\mathrm{d}t} µ$.
On obtient donc l’équation différentielle :
$µ mc \frac {\mathrm{d}T}{\mathrm{d}t} = \frac {T_{ext}-T}{R_{th}} µ$
8.2. On se ramène à la forme connue de ce type d’équation différentielle : $* f’+af=b*$, qui a pour solution $*Ke^{-at}+ \dfrac ba*$.
$µ
\begin{aligned}
\frac {\mathrm{d}T}{\mathrm{d}t} &= \frac {T_{ext}-T}{mcR_{th}} \\
\frac {\mathrm{d}T}{\mathrm{d}t} + \frac 1{mcR_{th}}T &= \frac {T_{ext}}{mcR_{th}}
\end{aligned}
µ$
Par identification, $* a= \dfrac 1{mcR_{th}}*$ et $* \dfrac ba = T_{ext} *$ donc $*θ_1*$ = 20 °C
De plus, $*T(0)*$ = 60 °C = $* θ_0 - θ_1*$ donc $* θ_0 *$ = 40 °C.
8.3. Après 48 h, $*T*$(48×3600) = 46,1 °C
Et après 15 jours, $*T*$ ≃ 20,0 °C
9. En supposant que l’air se comporte comme un gaz parfait, on a : $µ \frac {P_1 V_1}{P_2 V_2} = \frac {nRT_1}{nRT_2} µ$ $*V_1*$ et $*V_2*$ sont identiques, donc $* \dfrac {P_1}{P_2} = \dfrac {T_1}{T_2} *$, d’où, si $*T_2*$ = 60 °C = 333 K, $*P_2*$ = 1,14 bar. Donc pas de problème de surpression.
10. Ce modèle suppose que les particules de gaz sont ponctuelles et n’interagissent pas entre elles. Ce problème n’est pas adapté pour des gaz constitués de « grosses molécules » ou des hautes pression (c’est-à-dire des molécules dont les dimensions ne sont pas négligeables devant l’espace entre les molécules) et pour des molécules polarisées interagissant entre elles.