P7. Lunette astronomique
Ce chapitre fait appel aux notions sur les lentilles convergentes vues en première au chapitre P7. Il est impératif que vous soyez parfaitement à l’aise avec ces notions.
Objet & image à l’infini
Avant de parler de la lunette astronomique en elle-même, il faut que j’éclaircisse quelques points.
Mon œil
Un œil normal est constitué de sorte que l’image d’un objet éloigné (à l’infini) se forme sur la rétine lorsqu’on n’accomode pas.
Accomoder, ça veut dire actionner des muscles de l’œil qui vont déformer le cristallin – qui est une lentille convergente – de manière à diminuer sa distance focale.
Lorsqu’on observe un objet « proche » – disons jusqu’à quelques mètres de distance de l’œil – sans même s’en rendre compte, on accomode pour que l’image de cet objet se forme bien sur la rétine et qu’on en ait une image nette. Si on ne fait pas ça, par exemple en gardant son regard « dans le vague », on ne perçoit qu’une image floue de l’objet, car l’image ne se forme pas sur la rétine, mais en arrière de la rétine.
Accomoder fatigue l’œil. Pour éviter cette fatigue, tous les instruments optiques dont l’utilisation consiste à regarder « à travers » (jumelles, microscope, loupe, téléscope…), forme une image à l’infini de l’objet observé.
Ça veut juste dire que les rayons issus d’un point de cet objet sont parallèles entre eux.
Objet à l’infini
Lorsqu’un objet est à l’infini, son image se forme dans le plan focal image de la lentille, c’est-à-dire le plan perpendiculaire à l’axe optique de la lentille et contenant F’.
En effet, lorsque $*\overline{\text{OA}}*$ = –∞, la relation de conjugaison $µ \dfrac 1{\overline{\text{OA’}}} - \dfrac 1{\overline{\text{OA}}} = \dfrac 1{f’} µ$ devient $µ \dfrac 1{\overline{\text{OA’}}} = \dfrac 1{f’} µ$ et donc $* \overline{\text{OA’}} = f’*$
Imaginons que A et B soient deux points à la surface de la Lune et qu’on forme une image de la Lune sur un écran.
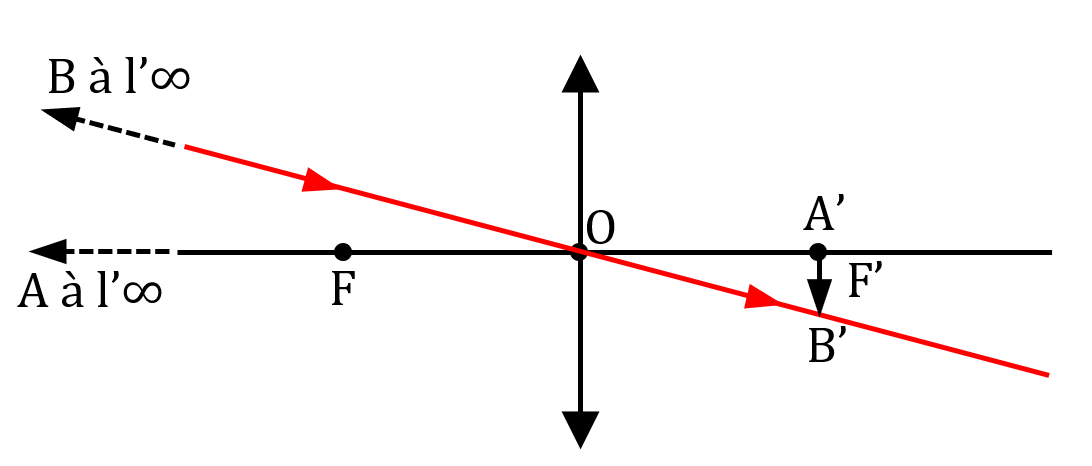
On obtiendra alors l’image de la Lune dans le plan focale de la lentille.
Objet au foyer
Si on place un objet exactement au foyer objet d’une lentille convergente, l’image formée sera une image à l’infini. Tous les rayons issus d’un même point de l’objet seront parallèle entre eux après la traversée de la lentille.
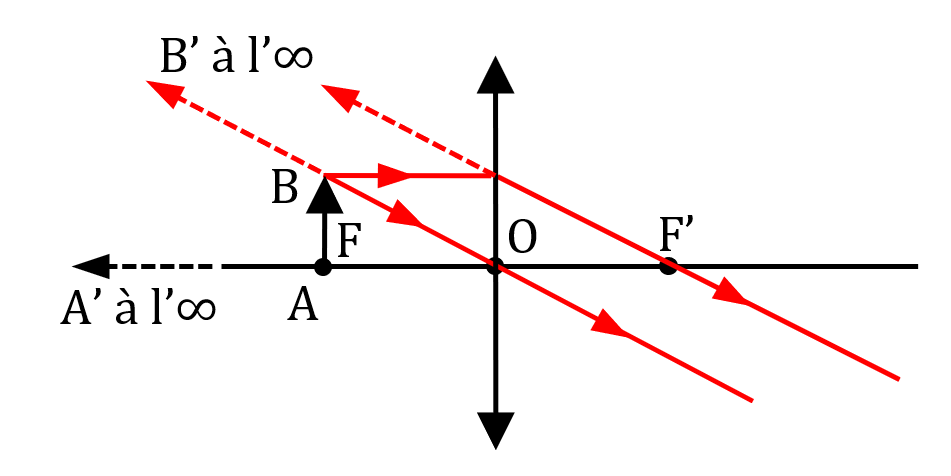
Lorsqu’on observe l’objet AB à travers la lentille, on verra son image (virtuelle, donc) à l’infini (c’est-à-dire que notre œil n’aura pas besoin d’accomoder) et sa taille sera plus grande que ce qui est vu à l’œil nu.
Très bonne remarque ! 😊 On ne peut effectivement pas parler de taille de l’image, puisque, celle-ci étant « à l’infini », sa taille est infinie aussi. Donc on ne peut pas parler de grandissement non plus.
Dans ces conditions, on parle de grossissement, c’est-à-dire de rapport de diamètres apparents. On reviendra plus tard dans ce chapitre sur la notion de grossissement.
Diamètre apparent
Le diamètre apparent d’un objet, c’est l’angle avec lequel on voit le voit. C’est sa « taille » apparente, qui dépend de sa taille réelle et de la distance à laquelle il se trouve de nous.
La Lune par exemple, fait à peu près 3500 km de diamètre, et se trouve à peu près à 400.000 km.
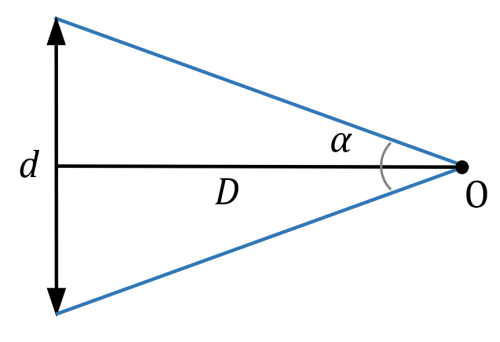
Un petit peu de trigo basique nous permet d’écrire que $µ \tan \frac \alpha 2 = \frac {d/2}D = \frac d{2D} µ$
Dans l’exemple de la Lune, l’angle $*\alpha*$ est très petit, de sorte que $*\tan \frac \alpha 2 \simeq \frac \alpha 2 *$. On obtient donc que $*\alpha = \frac dD = *$ 8,75·10-3 radian (soit 0,50°).
Le diamètre apparent du Soleil, vu depuis la Terre est à peu près le même (0,53°)
On réutilisera cette notion un peu plus tard lorsqu’on s’intéressera au grossissement d’une lunette astronomique.
Modèle de la lunette astronomique
- Représenter le schéma d’une lunette afocale modélisée par deux lentilles minces convergentes ; identifier l’objectif et l’oculaire.
- Représenter le faisceau émergent issu d’un point objet situé « à l’infini » et traversant une lunette afocale.
Une lunette astronomique (à ne pas confondre avec la lunette de Galilée ou encore le télescope) est l’association de deux lentilles convergentes placée l’une derrière l’autre, et partageant le même axe optique. Le principe est simple, mais astucieux : une première lentille, l’objectif forme l’image réelle d’un objet très éloigné. Cette image est appelée image intermédiaire.
Une deuxième lentille, l’oculaire, forme une image à l’infini de l’image formée par l’objectif.
Objectif
Comme les objets observés par une lunette astronomique sont très éloignés (et donc que $*\overline{\text{OA}}*$ ≃ ∞), leur image se forme dans le plan focal image de l’objectif. Cette image est appelée « image intermédiaire » car ce n’est pas celle qu’on observe en regardant dans la lunette.

Oculaire
L’oculaire est une lentille convergente que l’on va utiliser comme loupe pour observer l’image intermédiaire de l’objet formée par l’objectif.
On s’arrange pour placer l’oculaire de manière à ce que l’image intermédiaire (jouant le rôle d’objet pour l’oculaire) soit au foyer objet de celui-ci.
De cette manière, l’image par l’oculaire de l’image intermédiaire sera à l’infini.
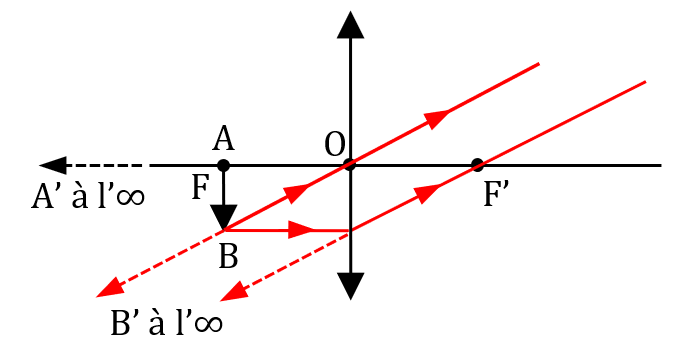
Combinaison objectif et oculaire
Lorsqu’on trace, sur un même schéma le trajet d’un rayon lumineux issu d’un point B à l’infini et passant par l’objectif puis par l’oculaire, on obtient le schéma suivant.
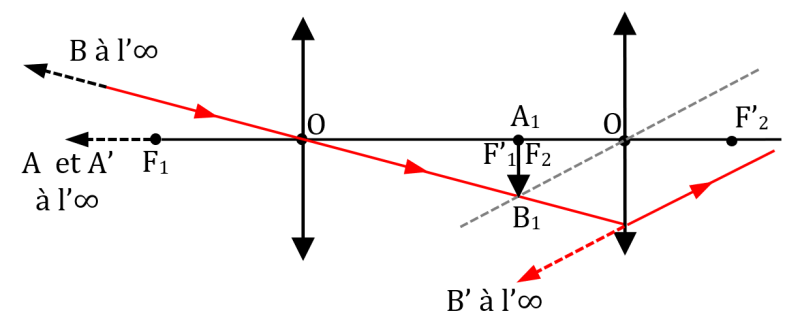
Remarques
- A1B1 est l’image intermédiaire de AB par l’objectif. Cette image iniermédiaire se forme au foyer image F’1 de l’objectif, qui est confondu avec le foyer objet F2 de l’oculaire (la lunette est construite comme ça).
- L’image de l’objet AB à l’infini se trouve elle-même à l’infini. C’est pour ça qu’on qualifie la lunette astronomique d’instrument afocale.
- L’angle apparent avec lequel on observe l’image A’B’ est plus grand que l’angle apparent de AB observé à l’œil nu. Sinon, la lunette n’a aucune utilité. On y renviendra dans le paragraphe suivant.
- La déviation du rayon passant par B1 et arrivant sur l’oculaire est obtenu en traçant un rayon « imaginaire » issue de B1 et passant par le centre optique de l’oculaire. Comme B1 se trouve dans le plan focal de l’oculaire, tous les rayons issus de ce point et sortant de l’occulaire seront parallèle entre eux.
- L’image est à l’envers par rapport à l’objet. Pas très gênant quand on observe une planète, mais un peu plus si on veut observer un oiseau 😊
Grossissement
- Établir l’expression du grossissement d’une lunette afocale.
- Exploiter les données caractéristiques d’une lunette commerciale.
Par définition, le grossissement $*G*$ d’une lunette est l’angle apparent de l’image observée divisée par l’angle apparent de l’objet observé à l’œil nu.
Sur le schéma ci-dessous, ces angles sont notés respectivement $*\beta*$ et $*\alpha*$.
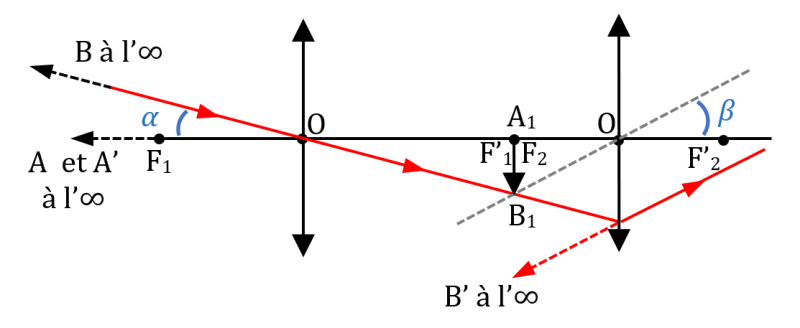
Là encore, un peu de trigo élémentaire va nous permettre de trouver une relation intéressante concernant le grossissement d’une lunette.
Remarquez que $* \tan \beta = \dfrac{A_1B_1}{f_2} *$ avec $*f_2*$ la distance focale de l’oculaire.
Remarquez de même que $* \tan \alpha = \dfrac{A_1B_1}{f_1} *$ avec $*f_1*$ la distance focale de l’objectif.
On en déduit donc que :
Si, par exemple, on associe un objectif de focale 50 cm et un oculaire de focale 5 cm, on obtiendra une lunette astronomique d’un grossissement de 10. Les objets observés avec cette lunette apparaîtront 10 fois plus gros qu’à l’œil nu.
TP Caractéristiques d’une lunette astronomique
- Réaliser une maquette de lunette astronomique ou utiliser une lunette commerciale pour en déterminer le grossissement.
- Vérifier la position de l’image intermédiaire en la visualisant sur un écran.
Objectif du TP : réaliser une maquette de lunette astronomique, observer la formation de l’image intermédiaire et déterminer le grossissement de la maquette réalisée.
Placement d’un objet à l’infini
Une lunette astronomique sert à observer des objets très éloignés (situé optiquement « à l’infini »). Comment obtenir un tel objet en salle de TP ?
- Réaliser le montage permettant d’obtenir l’objet à l’infini qui sera observé avec la lunette astronomique.
Objectif et image intermédiaire
- Placer sur le banc optique la lentille de 30 cm de focale (après avoir vérifier cette distance focale approximativement) de manière à obtenir une image intermédiaire.
- Mettre en évidence cette image intermédiaire et vérifier qu’elle se forme bien au foyer image de l’objectif.
Occulaire et grossissement
- Placer sur le banc la lentille de 15 cm de focale (après avoir vérifier cette distance focale approximativement) de manière à obtenir une image finale à l’infini.
- Observer l’image finale à travers cette lentille.
- Déterminer le grossissement de la lunette réalisée.
Éléments de réponses
Utilisation d’une lunette astronomique
On souhaite observer un cratère de 100 km sur la Lune. La limite de diamètre apparent pour qu’un objet soit visible à l’œil nu est de 0,02°.
On utilise une lunette astronomique ayant un objectif de focale $*f_1*$ = 70 cm et un oculaire de focale $*f_2*$ = 20 mm.
1. Ce cratère est-il observable à l’œil nu ? On rappelle que la distance Terre-Lune est d’environ 400.000 km.
2.a. Sur un schéma, tracer la marche de deux rayons lumineux issus des extrémités du cratère à travers la lunette.
2.b. Expliquer pourquoi la lunette astronomique est qualifiée d’« afocale » et quel est l’intérêt de cette caractéristique.
3.a Démontrer que le grossissement d’une lunette astronomique vaut $* G = \dfrac {f_1}{f_2} *$.
3.b. Ce cratère est-il observable avec cette lunette astronomique ?
Correction
1. Diamètre apparent $*\alpha*$ tout petit, donc $*\alpha = \frac dD = \frac {100}{400.000}*$ = 2,5·10-4 rad.
En degré : 0,014°.
Donc le cratère n’est pas visible à l’œil nu.
2.a. Voir cours.
2.b. La lunette forme une image à l’infini d’un objet lui-même à l’infini (définition d’un instrument afocal).
Ceci permet de voir l’image de manière nette sans avoir à accomoder et donc sans fatiguer l’œil.
3.a. Voir cours.
3.b. Le grossissement de cette lunette vaut 70÷2 = 35.
Donc le diamètre apparent du cratère vu à travers la lunette vaut 0,014×35 = 0,49°
Ce diamètre apparent est supérieur à la limite de 0,02°, donc il est visible à travers la lunette.
Pour aller plus loin
Le diamètre de l’objectif va conditionner la quantité de lumière reçue provenant de l’objet. Ainsi, plus l’objectif est grand, plus la quantité de lumière collectée sera importante.
Malheureusement, plus une lentille est grande, plus ses aberrations chromatiques et géométriques seront importantes – autrement dit, moins l’image obtenue sera nette.
C’est d’ailleurs pour ça qu’on préfère le télescope (où la lentille convergente est remplacée par un miroir parabolique convergent – pour lequel les abérration chromatique n’existe pas et les aberrations géométriques n’existent que dans la mesure où sa surface n’est pas parfaite) à la lunette astronomique.
Plus la focale de l’oculaire est petite par rapport à la focale de l’objectif, plus le grossissement sera fort. Mais (parce que – oui – il y a un mais, comme toujours) plus la lumière récoltée par l’objectif sera « diluée » dans l’image formée et donc moins cette image sera lumineuse.
Comme toujours, la mise en pratique de concepts théoriques se heurte à des limitations techniques avec lesquelles on doit trouver des compromis
Quelques ordres de grandeur de grossissement
Une paire de jumelles a un grossissement généralement compris entre 8 et 12. Ce grossissement est suffisant pour voir les satellites galiléens de Jupiter ainsi que les reliefs de la Lune.
Le grossissement d’une lunette amateur bon marché peut aller jusqu’à 50. Si vous vassez votre tirelire, vous pourrez monter jusqu’à 100 ou 200, mais attention : encore faut-il que les conditions atmosphériques soient bonnes pour en profiter.
Les télescopes actuels ont des diamètres immenses (39 m de diamètre pour le E-ELT). À ce stade, le principe est de récolter suffisament de lumière pour observer des objets très peu lumineux (une petite galaxie aux confins de l’Univers). Le grossissement du E-ELT est d’environ 18.000, même si cette notion est plus complexe dans ce cas. Pour pouvoir profiter d’un tel grossissement, il dispose d’une optique adaptative, permettant de corriger 1000 fois par seconde les perturbations de l’atmosphère et les vibrations de la structure dues au vent.
Révision & entraînement
Lunette astronomique
Cet exercice a été donné en devoir en 2020/2021.
Une lunette astronomique est constituée de deux lentilles convergentes. Une première, notée L1, de grande distance focale $*f’_1*$ et une deuxième, notée L2, de distance focale $*f’_2*$ beaucoup plus courte que L1.
Le foyer image F’1 de L1 coïncide avec le foyer objet F2 de L2.
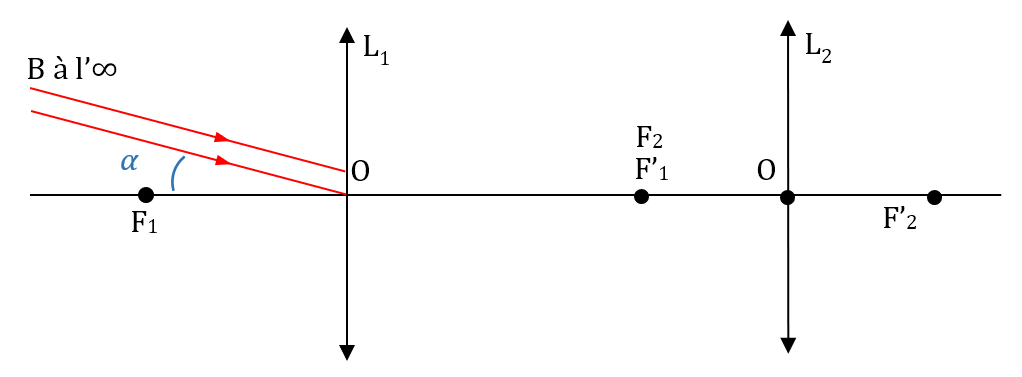
1. Tracer de manière propre et rigoureuse le cheminement de deux rayons issus d’un point B à l’infini à travers la lunette astronomique.
2. Après avoir défini ce que le grossissement d’une lunette astronomique, démontrer que : $µ G = \frac {f’_1}{f’_2} µ$
3. L’image intermédiaire formée par l’objectif est-elle réelle ou virtuelle ? Justifier.
4.a. Pourquoi qualifie-t-on la lunette astronomique d’instrument afocal ?
4.b. Quel est l’intérêt de former l’image à l’infini ?
5. Un astronome amateur dispose d’une lunette dont la focale de l’objectif est de 600 mm et celle de l’oculaire est de 10 mm.
Il observe Mars alors qu’elle se trouve à 80 millions de km. Peut-il espérer discerner le volcan Olympus Mons, d’un diamètre de 650 km, avec sa lunette ?
On rappelle que le pouvoir de résolution de l’œil est de 0,02°.
Correction
1. sur schéma.
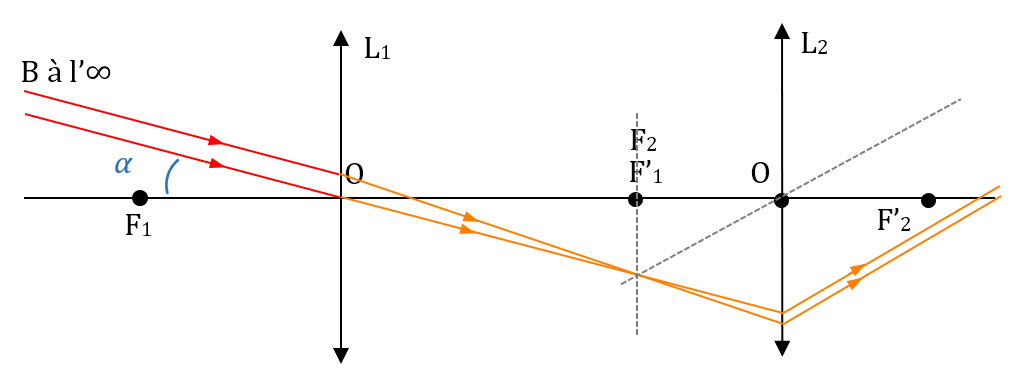
2. Grossissement = rapport du diamètre apparent de l’image sur le diamètre apparent de l’objet. Démonstration : voir cours.
3. L’image est réelle car elle est formé par une intersection réelle de rayons lumineux.
4.a. Elle donne une image à l’infini d’un objet à l’infini.
4.b. Permet à l’œil d’éviter d’accomoder.
5. Diamètre apparent d’Olympus Mons à l’œil nu : 8,13·10-6 radian soit 4,7·10-4 degré.
La lunette a un grossissement de 600÷10 = 60.
Diamètre apparent d’Olympus Mons par la lunette : 0,028° > 0,02°.
Il peut donc espérer voir le volcan.