A0-2.B. Accélérateur linéaire Linac2 du CERN

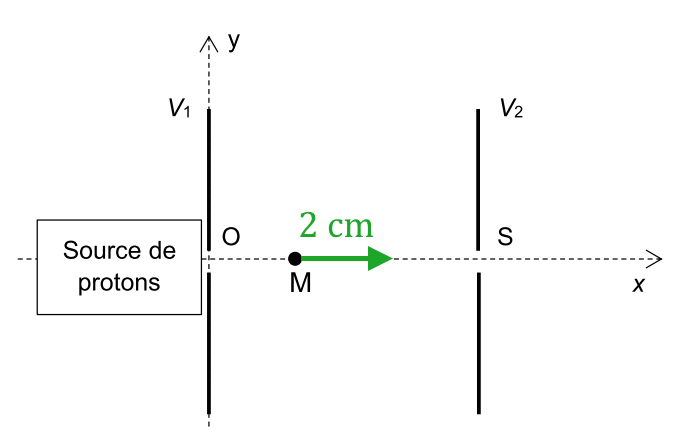
1. Accélération initiale des protons dans un premier condensateur plan

1.1. Le champ électrique doit être orienté de manière à ce que l’accélération des protons se fasse vers les $*x*$ croissants.
Sa norme vaut $*E*$ = 2,00 MV ÷ 0,100 m = 20,0 MV·m^-1.

1.2. On peut calculer directement le rapport $*\dfrac {F_e}P = \dfrac {eE}{m_pg} \approx *$ 2·10¹⁴. La valeur de la force électrique est donc environ 2·10¹⁴ fois plus grande que celle du poids. Le poids du proton est donc complètement négligeable dans la situation présentée.

1.3. D’après la RFD, comme la seule force non négligeable qui s’applique sur le proton est la force électrique, on a $*e\vec{E} = m_p\vec{a}*$ donc : $µ \vec{a} = \frac {e\vec{E}}{m_p}µ$

1.4. Le théorème de l’énergie cinétique dit que $*\Delta E_C = \sum W(\vec{f})*$. Ici, la seule force est la force électrique $*\vec{F}_e = e\vec{E}*$.
Son travail vaut $*W(\vec{F}_e) = eEd·\cos 0 = eU*$.
Donc $*\Delta E_C = E_C(\mathrm{S}) - E_C(\mathrm{S}) = eU*$.

1.5. La vitesse du proton en O est nulle. Donc on peut écrire $*\frac 12 m_pv_S^2 = eU*$.
Soit $*v_S = \sqrt{\dfrac{2eU}{m_p}} = *$ 2,53·10⁷ m·s^-1.
C’est beaucoup ! (Que dire de plus ? Que ça représente 8,4 % de $*c*$ ?)
Notons au passage que le résultat devrait être exprimé avec deux chiffres significatifs (donc 2,5·10⁷) car $*e*$ n’a que deux chiffres significatifs…

2. Principe du Linac2 – accélérateur linéaire

2.1. À $*t = \frac T4*$, $*U_A \gt*$ 0 et donc $*V_A \gt V_B*$
Les tubes n°1 et 3 sont donc positifs et le tube n°2 est négatif. Le champ électrique est orienté du $*\ominus*$ vers le $*\oplus*$.

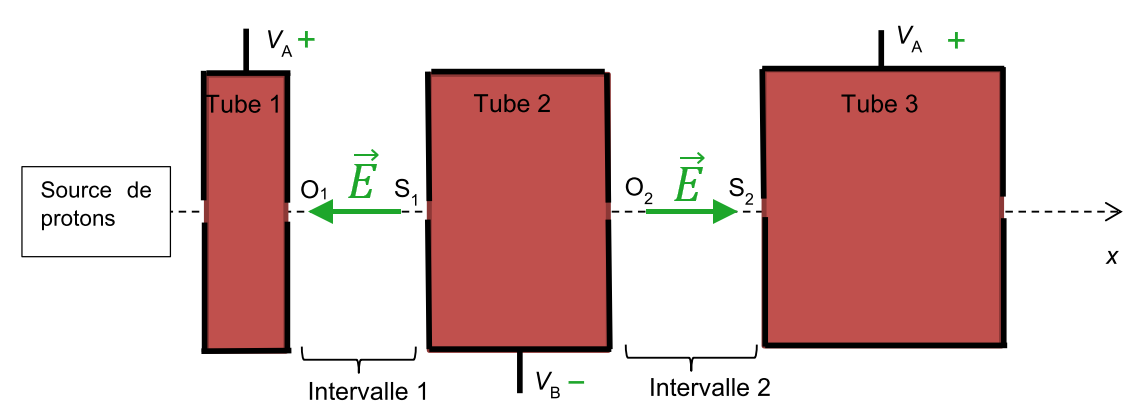
2.2. À $*t = \frac {3T}4*$, $*U_A \lt*$ 0 donc le sens de $*\vec{E}*$ est inversé.

2.3. À chaque fois que le proton sort d’un tube, il faut que le champ électrique soit orienté de tel sorte qu’il augmente la vitesse du proton.
Or d’après les branchements indiqués sur le schéma, à un moment donné, le sens du champ électrique dans l’intervale $*i*$ et le sens opposé du champ électrique dans les intervales $*i-1*$ et $*i+1*$.
Donc si le champ dans l’intervale $*i*$ accélère le proton, celui-ci doit arriver dans l’intervale $*i+1*$ quand le champ dans cet interval aura changé de sens, soit une demi-période plus tard.

2.4. Le proton étant de plus en plus rapide, la distance parcourue en une demi-période (donc la longueur des tubes) est de plus en plus grande.