2.2 Production et stockage de l’électricité
Production d’électricité sans combustion
- Décrire des exemples de chaînes de transformations énergétiques permettant d’obtenir de l’énergie électrique à partir de différentes ressources primaires d’énergie.
- Calculer le rendement global d’un système de conversion d’énergie.
La majeure partie de l’électricité produite dans le monde implique une combustion de ressources fossiles (charbon, pétrole, gaz), génératrice de CO2. Le CO2 est le principal gaz responsable du changement climatique. Il faut donc trouver d’autres moyens de produire de l’électricité.
Quelle sont les modes de production de l’électricité qui n’impliquent pas de combustion ?
Conversion d’énergie mécanique
On l’a vu au chapitre précédent, la conversion d’énergie mécanique en énergie électrique implique un alternateur.
Les sources d’énergie mécanique dans la Nature sont le vent (utilisé par les éoliennes) et le mouvement de l’eau (utilisé par les barrages hydroélectriques, les hydroliennes et les usines marémotrices).
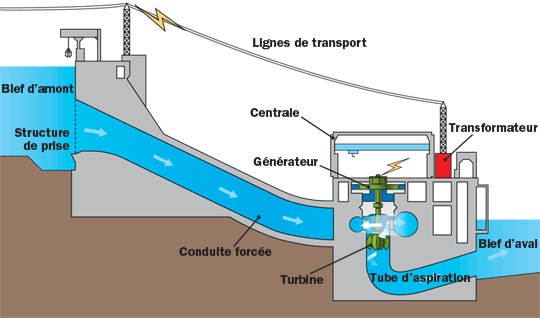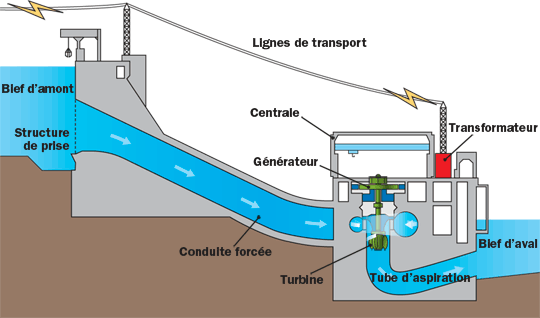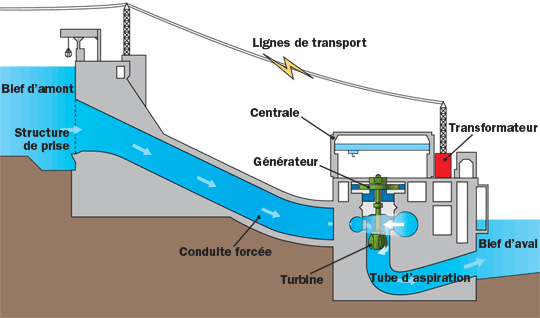
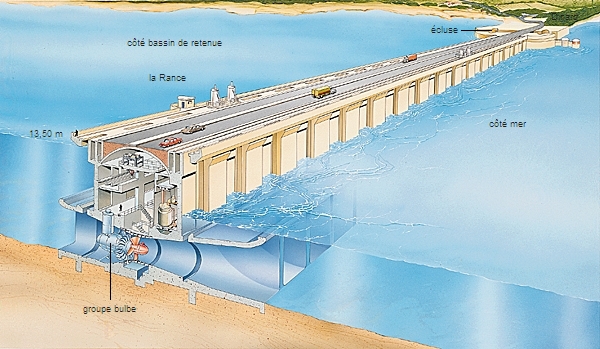

Conversion d’énergie thermique
Ces dispositifs fonctionnent à partir d’une source de chaleur intense qui permet de former de la vapeur d’eau sous pression. Cette vapeur d’eau entraîne une turbine reliée à un alternateur qui produit du courant électrique.
Le principe est absolument le même que pour les centrales à combustion. Seule la source de chaleur change : elle n’est pas due à la combustion de combustible fossile.
- Centrale nucléaire : la chaleur est produite par la fission nucléaire d’uranium 235.
- Centrale solaire thermique : la chaleur est produite par une concentration des rayons solaires à l’aide de grands miroirs paraboliques.
- Centrale géothermique : la source de chaleur est géologique. Il faut donc se trouver dans une région ayant une activité volcanique.
Conversion d’énergie radiative
Il s’agit des panneaux photovoltaïques, dont nous avons déjà largement parlé dans le chapitre précédent.
Conversion d’énergie chimique
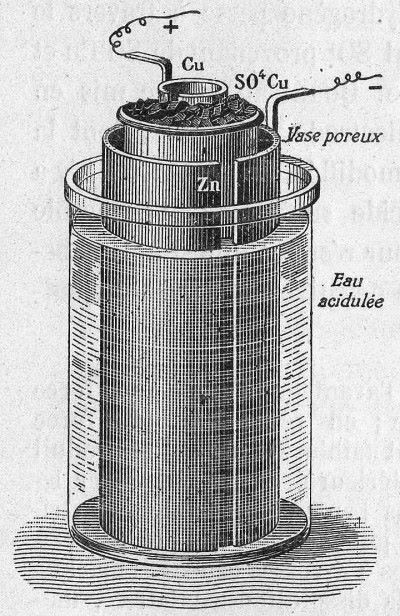
C’est historiquement, la première forme de production de l’énergie électrique (milieu du XIXe siècle). Dans une pile, deux réactifs échangent des électrons au cours d’une réaction chimique qui se déroule à l’intérieur de la pile.
Stockage de l’énergie
À moins de produire de l’énergie au moment même où on en a besoin, et dans la quantité exacte dont on a besoin, le stockage de l’énergie est un aspect majeur de son utilisation, au même titre que sa production.
Le pétrole a cet avantage très important de pouvoir être stocké facilement. Il suffit d’un réservoir. Mais stocker de l’énergie électrique produite par des sources intermittentes n’est pas un problème facile à résoudre. Il existe néanmoins plusieurs solutions dont bien-sûr aucune n’est parfaite. 😅
Accumulateurs
Les accumulateurs sont des piles rechargeables. Lorsqu’ils se déchargent, l’énergie chimique des réactifs est transformée en énergie électrique grâce à une réaction chimique. Mais il est possible d’inverser cette réaction chimique en apportant de l’énergie électrique. C’est ce qu’on appelle « recharger » une pile ou un batterie. Il s’agit ici d’un stockage d’énergie sous forme chimique.
La capacité d’un accumulateur est la charge qu’il est capable de stocker (exprimée la plupart du temps en Ampère-heure A·h). Par exemple, une batterie capable de stocker 80 A·h peut fournir un courant de 10 A pendant 8 heures, ou encore un courant de 5 A pendant 16 h, etc.
| $µ Q = I·\Delta t µ$ | $*Q*$ : charge (A·h) $*I*$ : intensité (A) $*\Delta t*$ : durée (h) |
L’énergie stockée dans accumulateur est le produit de sa charge par la tension à ses bornes.
| $µ E = Q·U = U·I·\Delta t µ$ | $*E*$ : énergie stockée (W·h) $*Q*$ : charge (A·h) $*U*$ : tension aux bornes de l’accumulateur (V) |
Les problèmes posés par les batteries sont importants :
- Poids important pour una quantité d’énergie stockée modeste (au mieux 265 W·h/kg).
- Coût important (135 € / kW·h de stockage pour les accus au lithium).
- Durée de vie limitées (4000 cycles de charges/décharges pour les accus lithium/ions s’ils sont bien traités).
- Impacts environnementaux (minage des ressources, fabrication, élimination en fin de vie).
- Risque d’incendie spontané, voire d’explosion (pour les accus au lithium).
Énergie stockée dans un accumulateur
1. Une batterie au lithium modèle 18650 a une capacité de 3000 mA·h et une tension de 3,7 V. Quelle énergie est-elle capable de stocker ?
2. Une batterie est rechargée sous une intensité de 7,5 A pendant 3 h. La tension à ses bornes est de 13,5 V. Quelle quantité d’énergie a-t-elle accumulée ?
Une batterie de voiture au plomb a généralement une capacité de 80 A·h et une tension de 12,5 V. Sachant qu’il ne faut pas la décharger de plus de 50 % sous peine de l’abimer, quelle énergie est-elle capable de fournir ? Comparer cette énergie à celle d’un fer à repasser d’une puissance de 1000 W utilisé pendant 30 minutes.
Correction
1. $*E*$ = 3×3,7 = 11,1 W·h
2. $*E*$ = $*I×\Delta t × U*$ = 7,5×3×13,5 = 300 W·h environ
3. Énergie totale stockée par la batterie : $*Q·U*$ = 12,5×80 = 1000 W·h. On dispose de la moitié de cette énergie, soit 500 W·h.
Énergie consommée par le fer à repasser : $*E*$ = $*P·\Delta t*$ = 500×0,5 = 500 W·h. Ces deux énergies sont égales.
Stockage d’énergie potentielle
L’énergie potentielle de pesanteur $*E_{pp}*$ est l’énergie d’une masse liée à son altitude.
| $µ E_{pp} = mgz µ$ |
$*m*$ : masse (kg) $*g*$ : intensité du champ de pesanteur (N·kg-1) $*z*$ : altitude (m) |
Si vous élevez une masse de 1 kg d’une hauteur de 1 m, vous lui communiquez une énergie de 1×9,8×1 = 9,8 J. Qu’elle gardera tant qu’elle se trouve à sa nouvelle altitude.
9,8 J, ce n’est pas beaucoup… Mais si vous élevez des milliers de tonnes d’eau de plusieurs dizaines de mètres, ça peut faire beaucoup d’énergie. Et c’est justement ce qui est fait au niveau de certains barrages électriques.
Des pompes amènent l’eau située dans le bassin inférieur vers le bassin supérieur. Ces pompes fonctionnent lorsque la quantité d’énergie produite est supérieure à la demande. L’énergie ainsi stockée peut être récupérée plus tard, en faisant passer cette eau par une turbine, comme dans un barrage hydroélectrique classique.
Stocker de l’énergie potentielle
On souhaite pouvoir stocker un excédent d’énergie solaire en pompant de l’eau de la partie basse d’un barrage à la partie haute.
Entre la partie basse et la partie haute, il y a une différence de hauteur de 50 m.
Dans cet exercice, on pourra arrondir l’intensité de la pesanteur à 10 N/kg pour simplifier les calculs.
1. Calculer l’énergie communiquée à 1 m3 d’eau lorsqu’on l’élève de 50 m. Donner le résultat en joules, puis en watt-heures.
2. On souhaite pouvoir stocker les besoins en énergie d’un foyer pour une journée, soit environ 15 kW·h. Quel volume d’eau faut-il faire passer de la partie basse à la partie haute, si on néglige toutes les pertes énergétiques ? Comparer ce volume à celui d’une salle de classe de 5 m de large, 8 m de long et 3 m de haut.
Correction
1. $*E = mgz =*$ 1000×10×50 = 500 kJ. 1 W·h vaut 3,6 kJ, donc 500 kJ équivalent à 500÷3,6 = 139 W·h environ.
2. Chaque mètre-cube permet de stocker 139 W·h. Si on veut stocker 15 kW·h, il faut alors 15.000÷139 = 108 m3 environ. Ce volume est voisin de celui-d’une salle de classe (5×8×3 = 120m3).
Rendement d’une chaîne énergétique
La production, le stockage et la restitution d’énergie implique plusieurs conversion. À chaque conversion, le rendement n’est pas de 100 %. Donc on a des pertes d’énergie (sous forme d’énergie thermique) à chaque élément de la chaîne énergétique.
Prenons par exemple la chaîne d’énergie permettant de transformer de l’énergie solaire en énergie électrique disponible quand on le souhaite (donc stockée dans des batteries).
Imaginons 1000 W·h d’énergie solaire qui arrive sur les panneaux. Le rendement des panneaux solaires étant de seulement 20 %, on n’en convertit donc que 200 W·h sur les 1000 reçus.
Cette énergie est ensuite convertie à la bonne tension pour pouvoir recharger les batteries par le régulateur MPPT (voir chapitre précédent). Un régulateur de bonne qualité peut avoir un rendement de 95 %. Il va donc envoyer 95 % des 200 W·h d’énergies électriques aux batteries, soit 190 W·h.
La charge des batteries n’a pas un rendement de 100 %. Une batterie au lithium a typiquement 90 % de rendement lors d’un cycle de charge-décharge. Cela signifique que pour 190 W·h envoyés à la batterie pour la charger, celle-ci ne restituera que 190×0,90 = 171 W·h.
Lorsque vous avez une chaîne de transformation, vous pouvez multiplier les rendement entre eux pour obtenir le rendement global : 1000×0,20×0,95×0,90 = 171.
À compléter
Correction
Impacts écologiques & autres contraintes
- Comparer différents dispositifs de stockage d’énergie selon différents critères (masses mises en jeu, capacité et durée de stockage, impact écologique).
- Analyser des documents présentant les conséquences de l’utilisation de ressources géologiques (métaux rares, etc.).
Si les différentes méthodes de production d’énergie électrique sans combustion et de stockage d’énergie citées dans ce cours ne sont pas émettrices de CO2 lors de leur fonctionnement, elles ne sont cependant pas sans impact sur l’Environnement, ni sans contraintes d’utilisation.
Il faut en effet prendre en compte différentes contraintes autres que l’émission de CO2 :
- le coût d’installation
- l’énergie nécessaire à la fabrication
- le caractère intermittent de la source d’énergie
- les contraintes environnementales nécessaires à l’utilisation du dispositif (climat ensoleillé, présence de vent, de la mer, de montagne…)
- la durée de vie du système
- les déchets générés par le dispositif en fin de vie
- l’exploitation de ressources rares
- le rapport « espace occupé » sur « énergie produite »
- l’impact esthétique
Activité notée
Pour le 25 novembre 2020 (au plus tard 22h), vous me remettrez une synthèse sur un des sujets ci-dessous.
Cette synthèse devra mentionner, si cela est pertinent :
- Les avantages & contraintes d’utilisations de ces dispositifs.
- Quelques valeurs clés pertinentes (rendement, puissance, densité énergétique) éventuellement comparée à d’autres dipositifs.
- Les impacts écologiques de ces dispositifs (positifs et négatifs).
Pour vous guider, imaginez que vous devrez présenter votre sujet en quelques minutes à une assemblée citoyenne, en vous appuyant sur votre document écrit.
Il ne vous est pas demandé de décrire le principe de fonctionnement.
Cette synthèse sera remise sur Google Classroom au format PDF. Elle comportera entre 1500 et 2500 caractères espaces inclus. Si vous le jugez pertinent, vous pouvez y insérer une image à caractère informatif (mais pas décoratif, ce n’est pas le but).
| Groupes | Sujets |
|---|---|
| Luka Š - Velimir | Panneaux solaires au silicum |
| Kruna - Marko | Centrale solaire thermique |
| Luka Đ - Konstantin | Centrale nucléaire |
| Ellena - Tea | Barrage hydroélectrique |
| Pavle - Uroš | Usine marémotrice |
| Tamara - Maya | Éoliennes |
| Natalija - Nina S | Batteries au lithium |
| Nadja - Gina | Pile à hydrogène |
| Andrija - Luka Z | Pompage-turbinage |
| Anastasija - Teodora | Géothermie de haute et moyenne énergie |
| Kristina - Jelena | Hydroliennes |
| Nina G - Marcos | Batteries au plomb |
| Andréas - Petar | Centrale biomasse |
Critères de notation
- Pertinence des informations fournies.
- Clarté de la présentation du document (présence de paragraphes clairs, éventuellement de puces pour séparer les idées, mise en gras des points importants).
- Qualité de la langue. Inutile de faire de belles phrases : des phrases courtes, claires et syntaxiquement correctes sont largement suffisantes.
- Qualité de la typographie : le document doit être correctement mis en forme (présence de titres et respect des règles typographiques – espace entre certaines ponctuations, usage des majuscules, pas de soulignement, etc) et sans faute de frappe (activez le correcteur orthographique).
Révision & entraînement
Pile à hydrogène
Dans une pile à combustible fonctionnant à l’hydrogène (souvent appelée « pile à hydrogène »), un réservoir de dihydrogène H2 alimente la pile. Il s’agit d’un des deux réactifs nécessaires, l’autre étant le dioxygène O2 directement pris dans l’air.
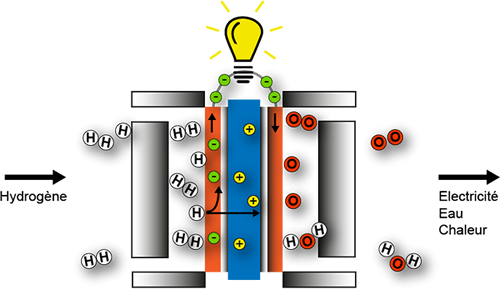
Une pile à hydrogène peut atteindre 55 % de rendement électrique. C’est-à-dire qu’elle peut convertir 55 % de l’énergie chimique qu’elle reçoit de ses réactifs en énergie électrique.
Mais le dihydrogène n’existe pas à l’état naturel. Il faut le former par électrolyse de l’eau, ce qui nécessite un apport d’énergie électrique. Le rendement de cette transformation est d’environ 70 %.
Enfin, pour être stocké en quantité raisonnable, le dihydrogène mis sous haute pression. Cela nécessite une consommation d’énergie correspondant à environ 20 % de l’énergie chimique qui peut être libérée par la combustion du H2.
1. Écrire l’équation-bilan de la réaction se déroulant au sein de la pile
2. Calculer le rendement global de la chaîne « électricité → dihydrogène → électricité ». Comparer ce rendement au rendement d’un cycle de charge et décharge d’une batterie au lithium, de l’ordre de 90 %.
La pile à hydrogène semble être la nouvelle solution « à la mode » pour faire face au défi énergétique.
3. Proposer au moins un argument en faveur de ce choix et au moins un autre contre ce choix. Vous pouvez vous documenter sur Internet.
4. Justifier que l’hydrogène n’est pas une source d’énergie, mais un moyen de stockage de l’énergie.
Correction
1. $*\ce{H2 + 1/2 O2 \rightarrow H2O}*$
2. Si on par de 100 J d’énergie électrique, on obtient 70 J d’énergie chimique. Cette énergie chimique peut produire 70×0,55 = 38,5 J d’énergie électrique par la pile à hydrogène. Enfin, l’énergie pour compresser le dihydrogène consomme 70×0,20 = 14 J. Donc le bilan global est de 38,5 – 14 = 24,5 J récupérer pour 100 J au départ, soit un rendement global de 24,5 %. C’est très faible comparé à une batterie au lithium.
3. En faveur de la pile à hydrogène : sa « recharge est très rapide ». Contre la pile à hydrogène : faible rendement.
Une tour de blocs de béton pour stocker l’électricité
La start-up suisse Energy Vault a conçu un système de stockage d’électricité exploitant l’énergie potentielle de pesanteur d’énormes blocs de béton.

Une grue à six branches de 120 mètres de hauteur hisse des blocs de béton de 8 m3 pesant près de 35 tonnes au sommet d’une tour (les blocs sont empilés les uns sur les autres) lorsque de l’électricité excédentaire sur le réseau doit être stockée et sont redescendus pour restituer de l’électricité lors des périodes de forte demande.
1. Calculer l’énergie potentielle de pesanteur d’un bloc de béton (prendre $*g*$ = 10 N·kg-1) situé à 100 m de hauteur.
Le rendement des meilleurs moteurs électriques et des meilleurs alternateurs vaut 90 %.
2.a. Calculer l’énergie électrique produite par la descente d’un bloc de béton de 100 m de hauteur jusqu’au sol.
2.b. Calculer l’énergie nécessaire pour hisser un bloc de béton du sol jusqu’à 100 m de hauteur.
2.c. Quel est le rendement global de ce système de stockage ?
Le rendement des tours de béton avoisinerait 85 % selon Energy Vault.
3. Cette valeur vous paraît-elle plausible ? Commentez-la, en la comparant avec le rendement d’un cycle de charge-décharge d’une batterie au lithium qui est d’environ 90 %.
4. Comparez l’énergie électrique produite par la descente d’un bloc de béton d’une altitude de 100 m à la consommation domestique quotidienne « moyenne » d’énergie électrique pour une personne, qui est d’environ 4 kW·h.
5. Une batterie au lithium capable de stocker 1 kW·h coûte environ 400 €. D’après la société Energy Vault, une tour est capable de stocker 20 MW·h. Une telle association coûte environ 2,7 millions d’euros. Est-ce une solution de stockage économiquement intéressante ?
6. Pour chaque point mentionnés dans le paragraphe Impacts écologiques & autres contraintes, analysez le cas des tours de béton d’Energy Vault.
Correction
1. $*E = mgz*$ = 35·103×10×100 = 35 MJ
2.a. Énergie électrique produite : 90 % de 35 soit 31,5 MJ.
2.b 35 MJ représente 90 % de l’énergie électrique utilisée par la moteur, donc l’énergie nécessaire vaut 38,9 MJ.
2.c. Rendement global : 0,9×0,9 ≃ 0,8 soit 80 %.
3. Cette valeur est compatible avec ce qu’on vient de calculer, quoiqu’un peu optimiste. Elle est comparable au cycle de charge-décharge d’une batterie au lithium en terme de rendement, ce qui est très intéressant.
4. 31,5 MJ = 31,5·106÷ 3600 ≃ 8,8 kWh soit 2,2 fois la consommation électrique quotidienne d’une personne.
5. Avec une tour d’Energy Vault, le coût de stockage du kW·h est d’environ 135 € par kW·h. C’est donc économiquement intéressant.
6. Analyse des impacts écologiques et autres contraintes des tour d’Energy Vault.
- le coût d’installation : on a vu dans l’exercice précédent que ce moyen de stockage est bien moins cher que l’utilisation des batteries au lithium.
- l’énergie nécessaire à la fabrication : la fabrication de blocs de béton ne nécessite pas une grande énergie.
- le caractère intermittent de la source d’énergie : ici, ce critère n’est pas pertinent car il s’agit uniquement d’un moyen de stockage.
- les contraintes environnementales nécessaires à l’utilisation du dispositif (climat ensoleillé, présence de vent, de la mer, de montagne…) : pas de contraintes particulières (à part peut-être éviter les zones à fort risque sismique…)
- la durée de vie du système : les blocs de bétons étant éternels (ou presque) la seule limite à la durée de vie du système est la grue. Mais il est possible de la changer sans avoir à reconstruire tout un nouveau système.
- les déchets générés par le dispositif en fin de vie : des blocs de béton et la grue, dont la majeure partie est constitué de métaux recyclables.
- l’exploitation de ressources rares : elle est extrêmement limitée car seuls les moteurs/alternateurs de la grue en nécessite.
- le rapport « espace occupé » sur « énergie produite » : l’exercice précédent montre que l’énergie stockée par un bloc de béton n’est pas énorme. Pour pouvoir stocker une quantité important d’énergie, il faudra certainement construire plusieurs tours.
- l’impact esthétique : il est bien présent, même s’il peut être atténué par une « architecture » bien pensée.