3-01. Généralités sur les graphes
Dans ce chapitre, nous allons aborder du vocabulaire et des notions propres aux graphes – indépendamment de tout aspect algorithmique. Rien de très complexe, mais il y a beaucoup de vocabulaire à maîtriser pour les chapitres à suivre.
Un peu d’histoire
Les graphes ont été introduits pour la première fois en 1735 par le mathématicien Leonhard Euler afin de répondre au problème appelé « Problème des sept ponts de Königsberg ».
En 1736, la ville de Königsberg (actuelle Kaliningrad) est construite autour de deux îles situées sur la Pregel et reliées entre elles par un pont. Six autres ponts relient les rives de la rivière à l’une ou l’autre des deux îles comme représentés sur la figure ci-dessous.
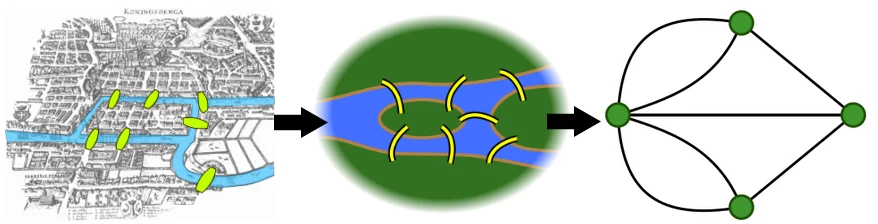
Les habitants se demandaient s’il existe ou non une promenade dans les rues de Königsberg permettant, à partir d’un point de départ au choix, de passer une et une seule fois par chaque pont et de revenir à son point de départ, étant entendu qu’on ne peut traverser la Pregel qu’en passant sur les ponts.
À partir de cette date, une théorie des graphes a été progressivement construite afin de répondre à des problèmes de plus en plus complexes.
Aujourd’hui, les graphes font partie des objets fondamentaux en algorithmique. En effet, leur structure relationnelle intrinsèque leur permettent de modéliser naturellement de très nombreux problèmes dans des domaines variés comme, par exemple :
- les réseaux de communications,
- les réseaux routiers,
- les optimisations de chemins,
- la gestion des ressources mémoires d’un ordinateur,
- les réseaux sociaux,
- le traitement automatique des langues,
- et bien d’autres choses…
Graphes
De manière simplifiée, un graphe est un ensemble de points reliés entre eux.
Ensemble : collection non ordonnée d’éléments distincts.
Par exemple {a, b, c} et {a, c, b} sont deux ensembles identiques.
Multi-ensemble : collection non ordonnée d’éléments pouvant apparaître plusieurs fois.
Par exemple {a, b, b, c, c} et {a, b, c, b, c} sont deux multi-ensembles identiques.
Graphes non orientés
Un graphe non orienté est un ensemble fini d’éléments appelés sommets associé à un multi-ensemble A de paires non ordonnées d’éléments appelées arêtes.
Une arête entre deux sommets $*u*$ et $*v*$ est notée indifférement par le couple $*(u,v)*$ ou par le couple $*(v,u)*$.
Deux sommets peuvent être reliés par plusieurs arêtes.
Quelques termes à connaître
- ordre du graphe : le nombre de sommets.
- taille du graphe : le nombre d’arêtes.
- boucle : arête reliant un sommet à lui-même.
- graphe non connexe : graphe pour lequel il existe au moins une paire de sommets entre lesquels aucun chemin n'existe. Le graphe se compose alors de plusieurs composantes connexes.
Exemples de graphes non-orientés
Dans le graphe non orienté $*G=(S,A)*$ de la figure 1a, on a :
$*S = \{a; b; c; e; f\}*$ et $*A = \{ (a,b); (a,e); (b,c); (c,e); (e,f) \}*$
Cette notation définit entièrement le graphe.
Mais… avec cette notation on ne sait rien de l’apparence du graphe… 🤔 Par exemple, on ne sait pas que le sommet $*e*$ est tout en haut !
Exact ! Et on s’en fiche. Regardez de nouveau la définition d’un graphe non orienté donnée au début de ce paragraphe. Un graphe, c’est des sommets et des arrêtes qui les relient. Vous avez une infinité de représentations graphiques possibles pour un même graphe, et elles sont toutes valables.
Graphes orientés
Dans un graphe orienté, les connexions reliant les sommets ont un sens, et sont appelées arcs.
Tout ce qui a été dit avant pour les graphes non orientés est toujours valable, sauf en ce qui concerne les arêtes. À la différence des arêtes, les arcs sont orientés, c’est-à-dire qu’ils ont un point de départ et un point d’arrivée.
Un arc partant d’un sommet $*u*$ et arrivant à un sommet $*v*$ est notée par le couple $*(u,v)*$.
Si le graphe n’a pas de boucle et a au plus un arc entre deux sommets quelconques, on parle de graphe simple.
Exemples de graphes orientés
Structure de graphes
Décrire la structure des deux graphes ci-dessous. Préciser leur ordre et leur taille.
Correction
Pour la figure 1, il s’agit d’un multi-graphe orienté non connexe, d’ordre 6 et de taille 8.
Pour la figure 2, il s’agit d’un graphe simple non orienté, d’ordre 5 et de taille 7.
Graphes valués
Dans un graphe valué, orienté ou non orienté, chaque arête ou arc est associé à une valeur (un nombre réel).
Le mot connexion désigne indistinctement une arête ou un arc. Je m’en servirai dans la suite de mon cours pour simplifier l’écriture lorsque c’est nécessaire.
Exemples de graphes valués
Adjacence, degré et voisins
Adjacence de sommets
Un sommet $*v*$ est adjacent à un sommet $*u*$ s’il est possible de passer de $*u*$ à $*v*$ par une arête (non orientée) ou un arc (orienté).
🖐️ N’oubliez pas qu’un arc est orienté. Un arc permettant de passer d’un sommet A à un sommet B ne permet pas de passer de B à A. Un sommet peut être adjacent à lui-même s’il a une boucle.
Reconnaître des sommets adjacents
Donner les sommets adjacents des sommets suivants :
- sommet e du graphe de la figure 1-a.
- sommet e du graphe de la figure 2-b.
- sommet a du graphe de la figure 2-b.
Correction
- a, c, f
- e, a
- b, c
Degré d’un sommet
Le degré d’un sommet est le nombre de connexions qui lui sont reliées.
Dans le cas d’un graphe orienté, on peut distinguer le degré entrant et le degré sortant.
Quelques remarques
- Un sommet est dit isolé s’il est de degré 0, c’est-à-dire s’il n’est connecté à aucun autre sommet.
- Degré minimal et degré maximal : ce sont le plus petit et le plus grand des degrés des sommets.
Déterminer le degré d’un sommet
1. Déterminer le degré de tous les sommets du graphe représenté à la figure 2-b
2. Quels sont les degrés minimal et maximal de ce graphe ?
Correction
1. degrés entrants en bleu, degrés sortants en rouge, degrés en noir.
2. degré maximal entrant : 3 ; degré maximal sortant : 2 ; degré maximal : 5
degré minimal entrant : 1 ; degré minimal sortant : 1 ; degré minimal : 3
Voisins d’un sommet
Un sommet A est voisin d’un autre sommet B si :
- dans un graphe non orienté, A et B sont reliés par une arête ;
- dans un graphe orienté, il existe un arc allant de A vers B (peu importe son sens). Si l’arc est orienté de A vers B, B est successeur de A et A est précédesseur de B.
Déterminer les voisins d’un sommet
Donner les sommets voisins des sommets suivants :
- sommet e du graphe représenté figure 1-a.
- sommet e du graphe représenté figure 2-b.
- sommet a du graphe représenté figure 2-b.
Correction
- a, c, f
- a, f
- b, c, e, f
Structure de graphes
Soit les deux graphes représentés ci-dessous.
1. Graphe de la figure 1
- Quels sont les sommets adjacents au sommet 2 et au sommet 3 ?
- Quels sont les voisins du sommet 5 ? On précisera ses prédécesseurs et ses successeurs.
- Quels sont les degrés entrant et sortant du sommet 4 ? Quel est son degré ?
- Le graphe a-t-il un sommet isolé ?
2. Graphe de la figure 2
- Quels sont les sommets adjacents au sommet 3 et au sommet 4 ?
- Quels sont les voisins du sommet 4 ?
- Quel est le degré du sommet 1 ?
- Quel est le degré minimal du graphe ? le degré maximal ?
Correction
Graphe 1
- sommets adjacents au sommet 2 → {2, 4, 5} et au sommet 3 → {}
- voisins du sommet 5 → 2 (prédécesseur) et 4 (prédécesseur et successeur)
- degrés entrant et sortant du sommet 4 → 2 et 2. Degré total → 4
- Pas de sommet isolé
Graphe 2
- sommets adjacents au sommet 3 → {1, 2} et au sommet 4 → {1, 2, 5}
- voisins du sommet 4 → {1, 2, 5}
- degré du sommet 1 → 4
- degré minimal du graphe → 2, degré maximal → 4
Chemins et connexité
Chemins entre deux sommets
Un chemin entre deux sommets A et B d’un graphe est une suite finie de connexions permettant de passer de A à B.
Quelques termes à connaître
- chemin simple : chemin constitué de connexions toutes distinctes (on ne repasse pas plusieurs fois par la même connexion).
- chemin fermé : chemin dont le sommet de départ et le sommet d’arrivé sont identiques.
- cycle : chemin simple fermé.
- longueur d’un chemin : nombre de connexions qui le composent
- distance d’un sommet $*u*$ à un sommet $*v*$ : plus petite des longueurs des chemins partant de $*u*$ et arrivant à $*v*$.
- diamètre du graphe la plus grande distance entre deux sommets quelconques.
Trouver des chemins entre deux sommets
1. Pour les graphes 2b et 2c, indiquer s’il existe toujours un chemin entre deux sommets quelconques et donner leur diamètre.
2. Donner un cycle de longueur 3 dans le graphe de la figure 3b.
3. Le graphe de la figure 3c est-il acyclique ? Quel est son diamètre ?
Correction
1. Dans le graphe 2b, il y a des arcs entrants et sortants à tous les sommets. Donc il existe toujours un chemin entre deux sommets quelconque. La distance la plus grande entre deux sommets est de 3. Donc le diamètre de ce graphe vaut 3.
Dans le graphe 2c, c est un sommet isolé. De plus, d est un sommet « puit », c’est-à-dire ne possédant que des arcs entrants. Donc il n’existe pas de chemin entre c et n’importe quel autre sommet, de même qu’entre d et n’importe quel autre sommet. Le diamètre de ce graphe est donc infini.
2. le chemin {e, a, f, e}, par exemple.
3. le graphe de la figure 3c possède plusieurs cycles : {a, a}, {b, b}, {c, c}, {a, b, a}, {a, c, a}, {a, b, a, c, a}… Son diamètre est de 2.
Chemins, distance et diamètre
Soit les deux graphes représentés ci-dessous.
1. Graphe de la figure 1
- Existe-t-il toujours un chemin entre deux sommets donnés ? Si non, quels sous-graphes vérifient cette propriété ?
- Donner un chemin de longueur 4 partant du sommet 1 et arrivant au sommet 5.
- Donner un cycle de longueur 5 partant du sommet 2.
- Dans le sous-graphe formé par les sommets 1, 2, 4 et 5, existe-t-il un chemin contenant une et une seule fois tous les sommets ?
- Quelle est la distance entre les sommets 1 et 5 ? entre les sommets 1 et 3 ?
- En déduire le diamètre du graphe.
2. Graphe de la figure 2
- Existe-t-il toujours un chemin entre deux sommets ? Si non, quels sous-graphes vérifient cette propriété ?
- Existe-t-il un chemin de longueur 3 entre les sommets 1 et 3 ?
- Le graphe est-il acyclique ?
- Existe-t-il un chemin contenant une et une seule fois toutes les arêtes ?
- Quelle est la distance entre les sommets 1 et 5 ? entre les sommets 3 et 5 ?
- Quel est le diamètre du graphe ?
Correction
Graphe 1
- Non, le sous-graphe {3,6} est isolé du sous-graphe {1, 2, 4, 5}. Mais le sous-graphe {1, 2, 4, 5} possède un chemin pour chaque paire de sommets.
- {1, 2, 2, 4, 5}
- {2, 2, 5, 4, 1, 2}
- Oui : {1, 2, 5, 4} ou encore {1, 2, 4, 5}
- distance entre les sommets 1 et 5 → 2, entre les sommets 1 et 3 → infinie
- Diamètre infini
Graphe 2
- Oui
- {1, 4, 2, 3}
- Non, il existe plusieurs cycles (ex. {1, 5, 4, 1})
- Oui, par exemple {1, 5, 4, 2, 3}
- distance entre les sommets 1 et 5 → 1, entre les sommets 3 et 5 → 2
- Diamètre 2
Connexité
Un graphe non orienté est dit connexe s’il existe un chemin entre deux sommets quelconques.
Un graphe orienté est dit fortement connexe si, pour toute paire ordonnée de sommets, il existe un chemin entre ces deux sommets.
Graphes eulériens et hamiltoniens
Pour information. Ces termes ne sont pas à connaître par cœur.
- chemin eulérien : chemin qui passe une seule fois par toutes les arêtes
- graphe semi-eulérien : graphe admettant un chemin eulérien
- cycle eulérien : chemin eulérien qui revient au sommet de départ.
- graphe eulérien : graphe admettant un cycle eulérien
- chemin hamiltonien : chemin qui passe une seule fois par tous les sommets
- graphe semi-hamiltonien : graphe admettant un chemin hamiltonien
- cycle hamiltonien : chemin hamiltonien qui revient au sommet de départ
- graphe hamiltonien : graphe admettant un cycle hamiltonien
Eulérien : on parle des connexions
Hamiltonien : on parle des sommets
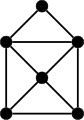
admettant un chemin eulérien.

sans lever le crayon
Vérifier qu’un graphe est semi-eulérien
Montrer que le graphe de la figure 1a est semi-eulérien. Préciser l’arête à ajouter pour que le graphe devienne eulérien.
Correction
Chemin eulérien : {e, a, b, c, e, f}. En ajoutant une deuxième arête entre e et f, on peut avoir le cycle eulérien suivant : {e, a, b, c, e, f, e}, ce qui rend le graphe eulérien.
Modélisation de la structure d’un site web
Le graphe ci-dessous modélise un site web constitué de six pages. Les flèches indiquent les liens entre les pages.
1. On est sur la page 1. Peut-on accéder à la page 6 en trois clics ? Que cela signifie-t-il pour le graphe ?
2. Montrer qu’il existe une page à partir de laquelle on peut visiter une et une seule fois tous les liens du site. Sur quelle page se retrouve-t-on à la fin ? Que cela signifie-t-il pour le graphe ?
3. Quel lien unique faut-il ajouter au site pour que, à partir de la page 1, on puisse visiter une et une seule fois tous les liens et revenir à la page de départ ? Que cela signifie-t-il pour le graphe ?
Correction
1. Oui (par exemple 1→4→5→6). Cela signifie qu’il existe un chemin de longueur 3 entre les sommets 1 et 6.
2. Il s’agit de la page 1 (1→2→3→4→5→6). C’est un chemin hamiltonien. Le graphe est donc semi-hamiltonien.
3. Il faut rajouter le lien 6→1. Ça rendrait le graphe eulérien.