Correction des annales de Tale spé
A0-1.1 Capture géologique du dioxyde de carbone
1. Au départ, l’eau distillée a un pH proche de 7 (couleur verte). Le $*\ce{CO2}*$ contenu dans l’air expiré se dissout dans l’eau distillée. La couleur orange indique un pH voisin de 5. Ceci met en évidence le caractère acide de la solution de $*\ce{CO2}*$ (à condition que l’on sache que dans l’air expiré, il y a du $*\ce{CO2}*$ et qu’il s’agit de la seule espèce ayant un caractère acide contenue dans l’air expiré… 🙄).
Remarque : l’eau distillée n’a pas un pH de 7 car elle est en contact avec le $*\ce{CO2}*$ de l’air qui fait diminuer son pH jusqu’à 5,65… 🙄
2. $*\ce{H2CO3}*$ fait partie du couple $*\ce{H2CO3/HCO3^-}*$. Il est donc capable de céder un ion $*\ce{H+}*$ et donc est bien un acide au sens de Brønsted.
Remarque : Brønsted s’écrit Brønsted et non Brönsted. 🙄
3. Chaque seconde, on dissout 70 g de $*\ce{CO2}*$ dans 1,8 L d’eau.
Ça représente une qdm $*n_\ce{CO2}*$ = 70÷44 = 1,59 mol.
En supposant que la réaction $*\ce{CO2(aq) + H2O(\ell) \rightarrow H2CO3(aq)}*$ est totale (ce qui n’est ni explicitement dit – même s’il y a une simple flèche, ni vrai 🙄), ça fait une concentration en acide carbonique $*\ce{[H2CO3]}*$ = 1,59÷1,8 = 0,88 mol·L-1.
4. Tableau d’avancement
| Avancement | $*\ce{\quad H2CO3 \quad + \quad H2O \; \rightarrow \quad HCO3^- \; + \quad H3O^+ \quad}*$ | |||
|---|---|---|---|---|
| 0 | $*C_S*$ | solvant | 0 | ≃ 0 |
| $*x_{éq}*$ | $*C_S-x_{éq}*$ | $*x_{éq}*$ | $*x_{éq}*$ | |
Remarque : on écrit une réaction non totale avec une double flèche… Ici, les concepteurs l’ont visiblement oublié. 🙄
5. La formule rigoureuse du $*K_A*$ est :
$µ K_A = \frac {
\dfrac{\ce{[A^-]}}{c^\mathrm{o}}·\dfrac{\ce{[H3O^+]}}{c^\mathrm{o}}
}{
\dfrac{\ce{[AH]}}{c^\mathrm{o}}}
µ$
C'est pour ça que l’énoncé parle du $*c^\mathrm{o}*$ qui vaut par définition 1 mol·L-1.
Après simplification de l’expression du $*K_A*$, on obtient :
$µ K_A = \frac {x_{éq}^2}{c^\mathrm{o}·(C_S-x_{éq})}µ$
En réarrangeant cette équation, on trouve l’équation $*x_{éq}^2 + c^\mathrm{o}K_Ax_{éq} - c^\mathrm{o}K_AC_S = 0*$.
6. $*x_{éq}*$ est forcément positif, donc $*x_{éq}*$ = 0,591 mmol·L-1. Du coup, on en déduit :
• $*\ce{[H2CO3]}*$ ≃ $*C_S*$ (le nombre de chiffres significatifs ne permet pas de noter une différence entre l’état initial et l’équilibre).
• $*\ce{[HCO3^-] = [H3O^+]} = *$ 0,591 mmol·L-1.
• $*\mathrm{pH} = -\log x_{éq} =*$ 3,23.
7. Lors de l’injection, le pH des eaux souterraines diminue à cause du caractère acide du $*\ce{CO2}*$ abordé dans l’exercice. La concentration en DIC augmente car le $*\ce{CO2}*$ réagit avec l’eau pour se transformer en acide carbonique et éventuellement en sa base conjuguée $*\ce{HCO3^-}*$ et en la base conjuguée de sa base conjuguée $*\ce{CO3^2-}*$. Pourquoi, dans un deuxième temps, y a-t-il une augmentation de pH et une diminution de la concentration en DIC pendant la phase d’injection (c’est-à-dire pendant la période grisée) ? Ce phénomène n’est pas explicable avec les documents donnés 🙄 (mais voir l’article original publié dans Science.)
A0-1.3 Un vol inaugural un peu particulier
A. Le retour des propulseurs latéraux sur Terre
1. Le principe d’inertie dit que $* \sum \vec{F}_{ext} = \vec{0} \Leftrightarrow \text{MRU ou immobile} *$ (programme de 1e)
Donc si les propulseurs ont un mouvement rectiligne uniforme, cela implique que $* \sum \vec{F}_{ext} = \vec{0}*$. Ils sont soumis à deux forces : leur poids et les forces de frottement dues à leur mouvement dans l’air. Ces deux forces doivent donc nécessairement se compenser pendant la période où ils ont un mouvement rectiligne uniforme.
2.1. Schéma de la situation
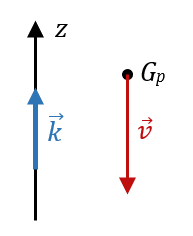
2.2. Définition du vecteur du centre d’inertie G : $µ \vec{v} \equiv { \mathrm{d}\overrightarrow{\mathrm{OG}} \over \mathrm{d}t } µ$
2.3. On a d’une part que $*\overrightarrow{\mathrm{OG}}*$ peut s’écrire : $*z(t)·\vec{k}*$, donc : $µ \vec{v} = { \mathrm{d}z \over \mathrm{d}t }·\vec{k} µ$ Comme une norme ne peut être que positive, on a alors que la norme $*v*$ de $*\vec{v}*$ vaut : $µ v = \left|{ \mathrm{d}z \over \mathrm{d}t }\right| µ$
3. On voit qu’à partir de 470 secondes environ, $*v(t)*$ décroît linéairement. Donc sa dérivée (l’accélération) est constante. Pour trouver sa valeur, il faut calculer la pente de la droite tracée en vert sur la figure ci-dessous.
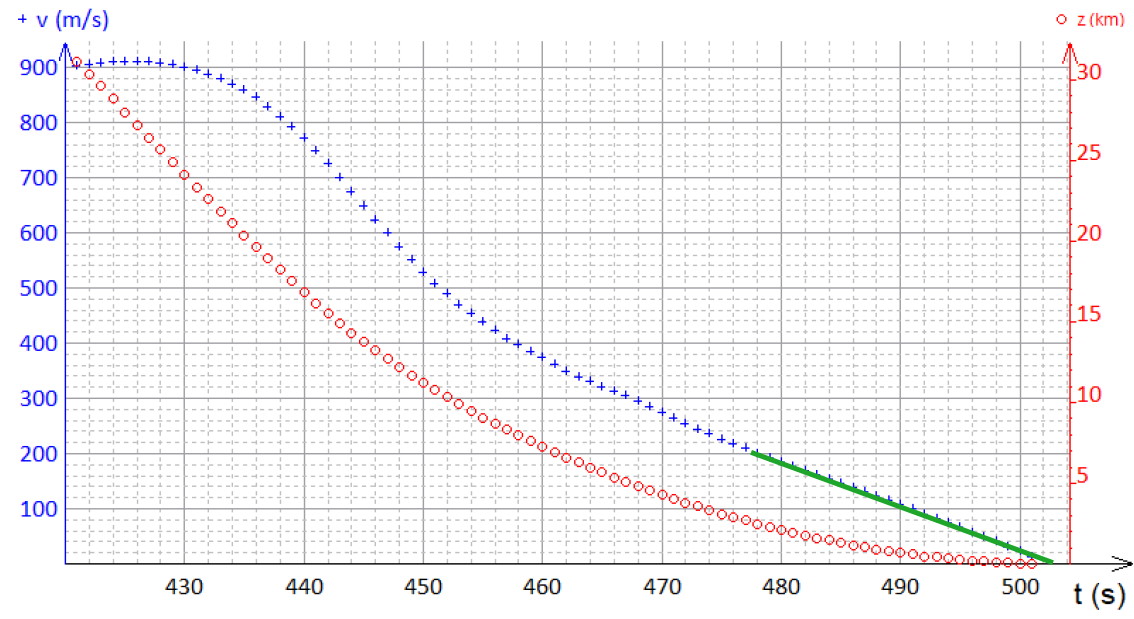
La vitesse de la fusée décroît de 200 m·s-1 en environ 24 s, ce qui fait une accélération dont la norme vaut 8,3 m·s-1.
4.1. La vitesse (verticale vers le bas) diminue, donc l’accélération est verticale vers le haut. La force du moteur est donc supérieure au poids. Il faut donc que le schéma en tienne compte.

4.2. D’après la RFD : $* \vec{F} + \vec{P} = m\vec{a}*$ donc $* F - P = ma*$ et donc $*F = ma + P =*$ 460 kN environ.
La poussée d’un moteur Merlin étant de 845 kN, on voit que la mise à en marche d’un seul moteur est largement suffisante pour assurer l’atterrissage.
B. Le mouvement de la planète Mars
1. Force exercée par le Soleil sur Mars
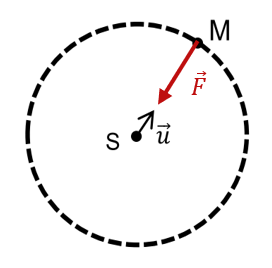
2. Expression de la force exercée par le Soleil sur Mars : $µ \vec{F} = - \cfrac {GM_SM_M}{d_{MS}^2}\vec{u} µ$ Mars est soumise à cette seule force extérieure. Donc la RFD devient ici : $µ - \cfrac {GM_SM_M}{d_{MS}^2}\vec{u} = M_M\vec{a} µ$ On obtient donc l’expression de l’accélération du centre de gravité de Mars : $µ \vec{a} = - \cfrac {GM_S}{d_{MS}^2}\vec{u} µ$
3.1. Expression du vecteur accélération dans le repère de Frenet : $µ \vec{a} = {\mathrm{d}v \over \mathrm{d}t }\vec{u}_t + \frac{v^2}R \vec{u}_n µ$ Ici, $*\vec{u_n}*$ = $*-\vec{u}*$ et $*R = d_{MS}*$. Donc, par identification des deux expressions de l’accélération, on en déduit que :
$* \cfrac {\mathrm{d}v} {\mathrm{d}t}=0*$ et $*\cfrac{v^2}{d_{MS}} = \cfrac {GM_S}{d_{MS}^2} *$
3.2. En reprenant ce qu’on a trouvé à la question précédente, on obtient l’expression de la valeur de la vitesse :
$µ v = \sqrt {\cfrac {GM_S}{d_{MS}}} µ$
En faisant l’application numérique, on obtient $*v*$ = 24,1 km·s-1.
Remarque : ne pas oublier de convertir $*d_{MS}*$ en mètres et garder 3 chiffres significatifs.
4. La période est la durée nécessaire pour que Mars parcoure son orbite, soit une longueur de $*2\pi d_{MS}*$. Donc $µ T = \frac{2\pi d_{MS}}{v} = 2\pi \sqrt {\cfrac {d_{MS}^3}{GM_S}} µ$ En faisant le calcul, on trouve $*T*$ = 5,94·107 s soit 687 jours soit environ 690 jours.
C. Davantage de carburant dans un même volume
1.1. L’énoncé dit que le LOX est refroidi, donc le transfert d’énergie thermique se fait du LOX vers le diazote liquide. Cela pourrait éventuellement entraîner une ébullition de ce dernier.
1.2. Il y a 287,4 t de LOX qui refroidissent de 10 °C.
Donc $*Q = mc\Delta T =*$ 287,4·103×1659×(-10) = -4,77 GJ
2. Pour établir l’expression de l’équation différentielle, on part de :
• Le flux thermique $*\phi*$ entre le réservoir et l’extérieur vaut $*\phi = hS(T_{\mathrm{air}}-T)*$.
• La chaleur $*Q*$ échangée pendant une durée $*\Delta t*$ vaut $*Q = \phi·\Delta t*$
• La chaleur $*Q*$ échangée pour une variation de température $*\Delta T*$ vaut $*Q = C·\Delta T*$
• La capacité calorifique $*C*$ du LOX vaut $*C = Mc*$
En réunissant ces équations, on obtient : $µ hS(T_{\mathrm{air}}-T)·\Delta t = Mc·\Delta T µ$ Que l’on peut réarranger en : $µ hS(T_\mathrm{air}-T) = Mc· \frac{\Delta T}{\Delta t} µ$ En faisant tendre $*\Delta t*$ vers 0, on obtient l’équation différentielle indiquée dans l’énoncé.
3. On sait que la solution d’une équation différentielle de la forme $*f' + af = b*$ s’écrit $*f(t) = K·e^{-at} + \frac ba*$
On réécrit l’équation différentielle de la question précédente pour lui donner cette forme :
$µ \frac{\mathrm{d}T}{\mathrm{d}t}+ \frac{hS}{Mc}T = \frac{hS}{Mc}T_\mathrm{air} µ$
Par identification, on obtient que $*\tau = \frac{Mc}{hS}*$.
De plus, on sait que $*T(0) = T_i = T_\mathrm{air} + A *$ donc $*A = T_i - T_\mathrm{air}*$
$*\tau*$ est la « constante de temps ». Plus elle est grande, plus le réchauffement sera lent.
4.1. Plus $*h*$ est grand, plus $*\tau*$ est petit et plus le réchauffement est rapide. Donc la courbe A (réchauffement rapide) est associée à $*h_2*$.
4.2. L’énoncé semble indiquer que le réchauffement du LOX est rapide. D’une part parce que le LOX n’est pas isolé thermiquement (il est dans un réservoir de métal directement au contact de l’air), et d’autre part par la phrase « Pour que l’augmentation de température du LOX dans le réservoir ne soit pas trop importante, le remplissage se fait pendant les 45 minutes précédant le décollage ».
Donc il semble que ce soit la courbe A qui modèlise le mieux le réchauffement du LOX.
Selon cette courbe, un réchauffement de 10 °C se fait en environ 30 minutes.
5. La vitesse du réchauffement dépend de $*T_\mathrm{air}-T*$. Si on prend 20 °C comme température de l’air, cela fait une différence initiale de 86 °C et de 76 °C après un réchauffement de 10 °C. Cela représente une faible variation relative (environ 12 %). Doncs la vitesse de réchauffement du LOX peut être considérée comme à peu près constante sur les 10 premiers degrés.
6. La question n’est pas claire, c’est le moins qu’on puisse dire. La durée du réchauffement (30 minutes pour gagner 10 °C) semble être vraiment brève. Ainsi, il y a peut-être un dispositif (comme une sorte de manteau) qui permet de limiter la convection de l’air et qui diminue la constante $*h*$ tant que la fusée n’est pas prête à partir. Je ne vois pas quel autre commentaire on pourrait faire en l’absence d’information supplémentaire.
A0-2.1. Dépolluer une eau avec des carapaces de crevettes
1.1. La chitine est naturelle car elle est produite par des animaux. Le chitosane est artificiel car il nécessite une manipulation humaine pour sa synthèse.
1.2 Motif de la chitine.
2.1. Pour trouver le motif de la chitosane, il suffit de remarquer que la liaison N–C de la fonction amide de la chitine a été rompue, et qu’un H vient se lier à l’azote.
2.2. Il s’agit de la fonction amine.
2.3. Intérêt : pouvoir chauffer le mélange réactionnel, sans évaporation des réactifs et sans problème de surpression.
- Sortie d’eau
- Réfrigérant à boules
- Entrée d’eau
- Ballon
- Chauffe-ballon
- Support élévateur
2.4. Définition du rendement : rapport de la qdm de produit obtenu sur la qdm maximale de produit qu’on peut obtenir selon la quantité de réactifs utilisés.
Masse molaire de la chitine à 4 motifs : 4×203 + 18 = 830 g·mol-1
Qdm initiale de chitine : 8÷830 = 9,64 mmol
Masse molaire de la chitosane à 4 motifs : 4×159 + 18 = 654 g·mol-1
Qdm expérimentale de chitosane obtenue : 6,12 mmol
Rendement : 63,5 % environ.
3.1. Le sulfate de cuivre absorbe fortement au-delà de 700 nm. Sa couleur est donc la couleur opposée au rouge, le cyan.
3.2. Protocole de dilution.
- Avec une pipette jaugée, prélever une volume de 2,0 mL de S.
- Verser dans une fiole jaugée de 10 mL.
- Compléter avec de l’eau distillée jusqu’au trait de jauge
- Boucher, agiter.
3.3. On commence par estimer le coefficient de proportionnalité $*k*$ entre l’absorbance et la concentration en $*\ce{Cu^2+}*$.
$*k*$ ≃ 1,13÷0,10 = 11,3 L·mol-1
L’idéal serait bien sûr de tracer le graphique $*A = f(c)*$ et de calculer le coefficient directeur de cette droite. Mais c’est trop long à faire pour une épreuve de bac.
Ensuite, on en déduit la concentration en ions $*\ce{Cu^2+}*$ du filtrat : $*C_f*$ = 0,30÷11,3 = 2,65·10-2 mol·L-1.
La concentration restant est de 26,5 % de la concentration initiale.
On en déduit qu’environ 74 % des ions $*\ce{Cu^2+}*$ initialement présents on réagit. Comme le chitosane est en excès, l’avancement de réaction est donc de 74 %.
4.1. La vitesse volumique de disparition (ou de consommation) d’un réactif est la valeur absolue de la dérivée de la concentration de ce réactif par rapport au temps $µ v_\ce{Cu^2+} = - \frac {\mathrm{d}[\ce{Cu^2+}]}{\mathrm{d}t} µ$
4.2. On trace la tangente à la courbe à $*t*$ = 10 minutes et on trouve son coefficient directeur (environ 0,63 mmol·L-1·min-1).
4.3. La concentration des ions $*\ce{Cu^2+}*$ baisse de moins en moins vite au cours du temps. La vitesse volumique de disparition diminue car la concentration des réactifs diminue également au cours du temp.
4.4. La ligne 19 du programme montre qu’on calcule une vitesse moyenne de disparition au cours du temps ($*\frac {- \Delta C} {\Delta t}*$) et non pas une vitesse instantanée (qui est $*- \frac {\mathrm{d}[\ce{Cu^2+}]}{\mathrm{d}t}*$ ).
4.5. On voit que la vitesse de disparition des ions $*\ce{Cu^2+}*$ est proportionnelle (à peu près) à leur concentration. Il s’agit donc bien d’une loi de vitesse d’ordre 1.
A0-2.B Accélérateur linéaire Linac2 du CERN
1. Accélération initiale des protons dans un premier condensateur plan
1.1. Le champ électrique doit être orienté de manière à ce que l’accélération des protons se fasse vers les $*x*$ croissants.
Sa norme vaut $*E*$ = 2,00 MV ÷ 0,100 m = 20,0 MV·m-1.
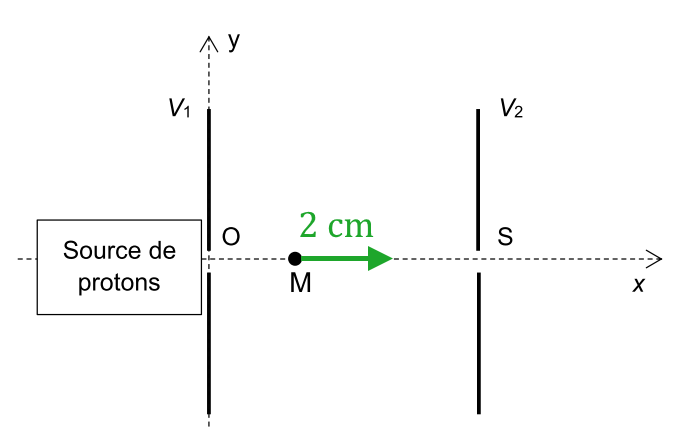
1.2. On peut calculer directement le rapport $*\dfrac {F_e}P = \dfrac {eE}{m_pg} \approx *$ 2·1014. La valeur de la force électrique est donc environ 2·1014 fois plus grande que celle du poids. Le poids du proton est donc complètement négligeable dans la situation présentée.
1.3. D’après la RFD, comme la seule force non négligeable qui s’applique sur le proton est la force électrique, on a $*e\vec{E} = m_p\vec{a}*$ donc : $µ \vec{a} = \frac {e\vec{E}}{m_p}µ$
1.4. Le théorème de l’énergie cinétique dit que $*\Delta E_C = \sum W(\vec{f})*$. Ici, la seule force est la force électrique $*\vec{F}_e = e\vec{E}*$.
Son travail vaut $*W(\vec{F}_e) = eEd·\cos 0 = eU*$.
Donc $*\Delta E_C = E_C(\mathrm{S}) - E_C(\mathrm{S}) = eU*$.
1.5. La vitesse du proton en O est nulle. Donc on peut écrire $*\frac 12 m_pv_S^2 = eU*$.
Soit $*v_S = \sqrt{\dfrac{2eU}{m_p}} = *$ 2,53·107 m·s-1.
C’est beaucoup ! (Que dire de plus ? Que ça représente 8,4 % de $*c*$ ?)
Notons au passage que le résultat devrait être exprimé avec deux chiffres significatifs (donc 2,5·107) car $*e*$ n’a que deux chiffres significatifs…
2. Principe du Linac2 – accélérateur linéaire
2.1. À $*t = \frac T4*$, $*U_A \gt*$ 0 et donc $*V_A \gt V_B*$
Les tubes n°1 et 3 sont donc positifs et le tube n°2 est négatif. Le champ électrique est orienté du $*\ominus*$ vers le $*\oplus*$.
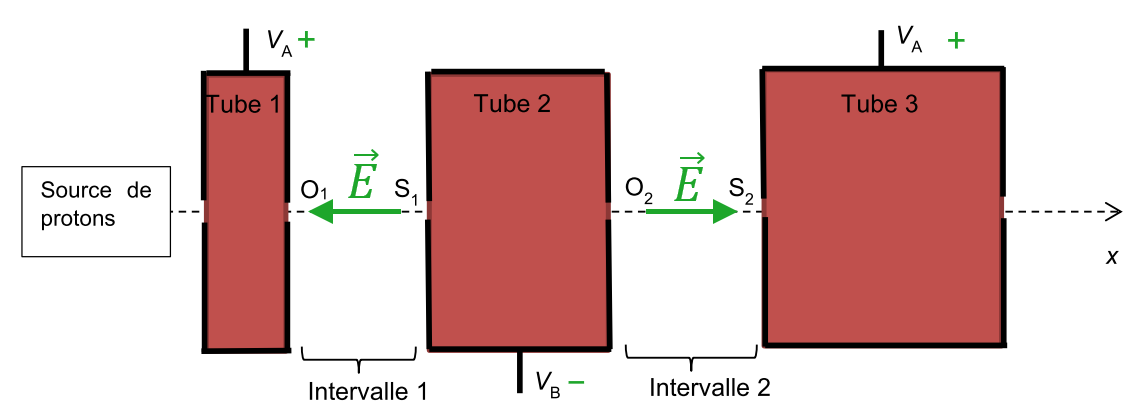
2.2. À $*t = \frac {3T}4*$, $*U_A \lt*$ 0 donc le sens de $*\vec{E}*$ est inversé.
2.3. À chaque fois que le proton sort d’un tube, il faut que le champ électrique soit orienté de tel sorte qu’il augmente la vitesse du proton.
Or d’après les branchements indiqués sur le schéma, à un moment donné, le sens du champ électrique dans l’intervale $*i*$ et le sens opposé du champ électrique dans les intervales $*i-1*$ et $*i+1*$.
Donc si le champ dans l’intervale $*i*$ accélère le proton, celui-ci doit arriver dans l’intervale $*i+1*$ quand le champ dans cet interval aura changé de sens, soit une demi-période plus tard.
2.4. Le proton étant de plus en plus rapide, la distance parcourue en une demi-période (donc la longueur des tubes) est de plus en plus grande.
2021-MET-2.1 L’aquarium récifal
3. Traitement des poissons contre les vers
3.1.1. Un seul carbone et fonction aldéhyde.
3.1.2. Formule semi-développée de C
Formule brute : $*\ce{C6H12O2}*$
3.1.3. Question sans intérêt, niveau collège, mais longue à traiter… 🙄
Il suffit de compter les différents éléments des réactifs (21 C, 30 H, 5 O et 2 N) et soustraire ces nombres aux éléments de F pour trouver… $*\ce{H2O}*$
2021-LIB.1 Préparation d’une bière brune aromatisée
1. Synthèse d’un ester au laboratoire
1. Il s’agit de l’hexanoate d’éthyle.
2. acide hexanoïque et éthanol
3. Accélère la réaction (chauffage) sans perte de vapeur (condensation dans le réfrigérant à boules).
4. espèce chimique qui augmente la vitesse d’une réaction donnée et dont la quantité à l’état initial est égale à la quantité à l’état final.
5. Pour l’alcool : masse = 20×0,789 = 15,8 g. Qdm = 15,8÷46,1 = 0,342 mol.
Pour l’acide : masse = 43×0,93 = 40,0 g. Qdm = 40÷0,344 mol.
D’après l’équation-bilan, il faut une qdm égale d’acide et d’alcool. Donc ces deux espèces sont bien en proportions stoechiométriques.
Qdm d’ester produite : 33,1÷144,2 = 0,223 mol
Rendement : 0,223÷0,342 = 0,65 (ou 65 %)
6. La synthèse est la plus lente lorsque la qdm d’acide décroît le plus lentement, c’est-à-dire pour la courbe A. Celle-ci tend vers le même minimum que la courbe B donc il s’agit d’un mélange 43 mL d’acide et 20 mL d’alcool. Donc A et B correspondent aux conditions expérimentales 1 et 3. D’autre part, on sait que la température est un facteur cinétique, donc A correspond aux conditions expérimentales pour lesquelles la température est la plus basse, soit les conditions 1.
Remarque : la question n’est pas très claire… 🙄 On ne peut pas vraiment parler ici de « concentration » des réactifs puisqu’ils ne sont pas en solution. Donc il est difficile de prévoir, d’après le cours et sans raisonner sur les graphiques, quelles seront les conditions expérimentales qui permettront une plus grande vitesse de réaction.
7. Il s’agit de la courbe C car cette courbe montre qu’une plus grande qdm d’acide a été consommée (et donc une plus grande qdm d’ester a été produite). On peut en déduire, en s’appuyant sur la réponse à la question précédente, qu’il s’agit des conditions expérimentales 2.
8. On peut éliminer le spectre n°1 qui ne montre pas la bande d’absorption $*\ce{C=O}*$. Le spectre n°3 présente une absorption plus large autour de 3000 cm-1 que le spectre n°2. Ceci est certainement dû à la présence de la liaison $*\ce{O-H}*$ dans l’acide. On peut donc associer l’ester au spectre n°2.