Équations différentielles

Une équation différentielle est une équation dont la ou les inconnues sont des fonctions ; elle se présente sous la forme d’une relation entre ces fonctions inconnues et leurs dérivées successives.

En spé SPC en classe de terminale, on ne va s’intéresser qu’aux équations différentielles d’ordre 1 (c’est-à-dire ne faisant intervenir qu’une fonction et sa dérivée première), linéaires (la fonction et ses dérivées sont à la puissance 1) et à coefficients constants (c’est-à-dire que les coefficients devant la fonction et ses dérivées sont constants).

Ce type d’équation différentielles peuvent être résolues de manière formelle.

De manière générale, la très grande majorité des équations différentielles ne peuvent pas être résolues de manière formelle. Mais que font les matheux ? 😅

Sans second membre

Il s’agit des équations différentielles linéaires d’ordre 1 sans second membre à coefficients constants (ouf !)

Leur forme générale peut se ramener à : $µ f'(x) + af(x) = 0 µ$ Leurs solutions sont de la forme $*f(x) = ke^{-ax}*$ avec $*k*$ un réel quelconque.
$*k*$ peut être déterminé si on connaît une valeur de $*f*$ pour un $*x*$ donné.

La solution est triviale si $*k*$ = 0. On a alors $*f(x)=0*$.

Quelques exemples

1. Résoudre l’équation différentielle $* 10f'(x) - 2f(x) = 0*$ avec $*f(2)*$ = –10.

2. Résoudre la même équation différentielle avec $*f(0)*$ = 0.

Soit $*p(t)*$ la fonction modélisant une population en fonction du temps. Le taux de variation de cette population est proportionnel à la population, de sorte qu’on peut écrire $* \dfrac {\mathrm{d}p}{\mathrm{d}t} = \alpha p*$ avec $*\alpha*$ un facteur qui dépend de la population dont on parle.
3.1. Trouver l’équation différentielle à laquelle obéit $*p(t)*$
3.2. Résoudre cette équation différentielle
3.3. Tracer l’allure de cette fonction selon le signe de $*\alpha*$
3.4. À quelle situation pourrait correspondre $*\alpha*$ > 0 ? Et $*\alpha*$ < 0 ?

Correction

1. Il faut d’abord se ramener à la forme connue $*f’+af=0*$. Dans ce cas, $*a*$ = 0,2.
On obtient donc, comme solution générale, $*f(x)*$ = $*Ke^{-0,2x}*$
Si $*f(2)*$ = –10, on peut écrire $*Ke^{-0,2×2}*$ = –10.
D’où $*K = \dfrac {-10}{e^{-0,4}} ≃ –14,9*$

2. On a la même solution générale : $*f(x)*$ = $*Ke^{-0,2x}*$ mais il faut que $*f(0)*$ = 0 et donc $*Ke^{0}*$ = 0 soit $*K*$ = 0.

3.1. $* \dfrac {\mathrm{d}p}{\mathrm{d}t} - \alpha p = 0 *$

3.2. $* p(t) = Ke^{\alpha t} *$

3.3. Allure de la fonction selon le signe de $*\alpha*$

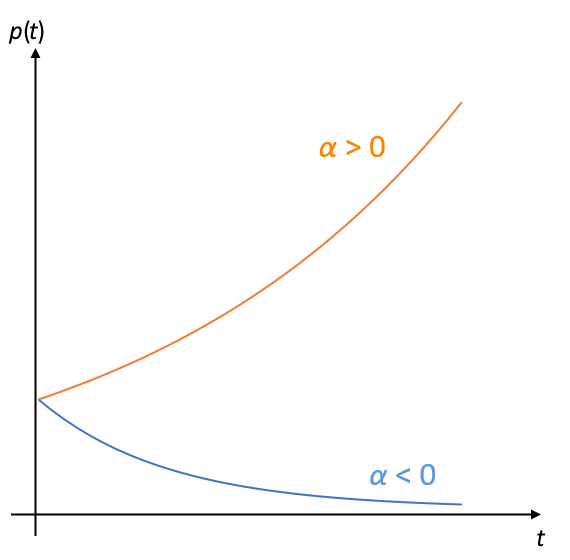
3.4. $*\alpha*$ > 0 pourrait correspondre à la croissance d’une population de bactéries placées dans des conditions idéales.
$*\alpha*$ < 0 correspond à la décroisance d’une population de noyaux radioactifs (souvenez-vous : on en parlait au premier chapitre d’Enseignement scientifique de première… On a même fait une activité dessus, à l’aide d’un tableur).

Avec second membre constant

Une deuxième type d’équations différentielles que vous devez savoir résoudre est les équations différentielles linéaires d’ordre 1 avec second membre à coefficients constants

Leur forme générale peut se ramener à : $µ f'(x) + af(x) = b µ$

Résolution

1. Proposer une solution triviale pour ces équations.

2. Montrer qu’une fonction exponentielle bien choisie + la solution triviale est également solution de cette équation différentielle.

3. Proposer une solution générale pour ce genre d’équations différentielles

Correction

1. $*f(x) = \frac ba *$

Les solutions d’une équation différentielle de la forme $* f'(x) + af(x) = b *$ avec $*a \in \mathbb{R}^* *$ et $*b \in \mathbb{R} *$ ont la forme : $µ f(x) = Ke^{-ax} + \frac ba µ$

avec $*K \in \mathbb{R} *$.

La connaissance d’un couple ($*x_0*$ ; $*f(x_0)*$) permet de fixer la valeur de $*K*$