Logarithmes & exponentielles

Une fonction exponentielle a pour expression $*f(x) = a^x*$ avec $*a \in \mathbb{R}_+*$.

Les fonctions exponentielles sont :

• continues, dérivables, strictement monotones et strictement positives sur tout $*\mathbb{R}*$
• donc bijectives de $*\mathbb{R} \mapsto \mathbb{R}_+^{*} *$
• Décroissantes si $*0 \lt a \lt 1*$
• Croissantes si $* a \gt 1*$ (ce qui sera toujours le cas en physique).

Le cas $*a*$ = 1 est inintéressant, puisque ça donne la fonction constante $*f(x) = 1*$

Voici leur allure :

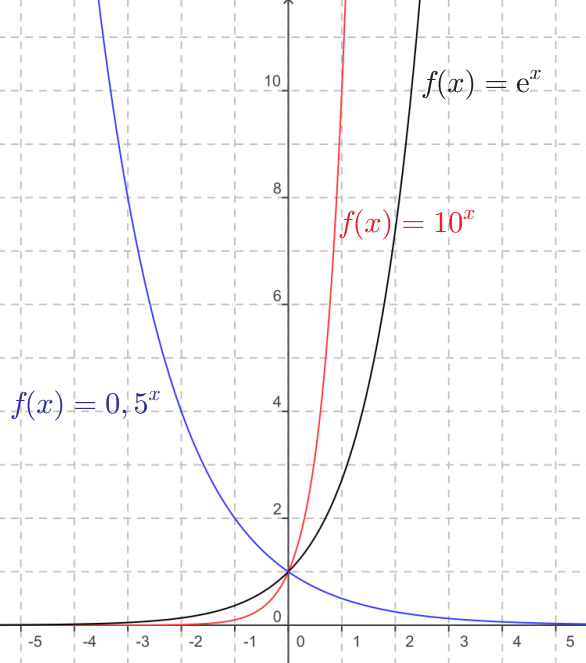
Deux exponentielles nous intéressent en physique et en chimique, l’exponentielle de base 10 et l’exponentielle de base $*\mathrm{e}*$.

Quelques propriétés

• $*a^x·a^y = a^{x+y}*$ (ça vous le saviez déjà)

• $*a^x = b \Leftrightarrow x = \log_a(b)*$ (très utile pour résoudre une équation)

• $*a^x = a^y \Leftrightarrow x = y*$ (très utile pour résoudre une équation)

• $*(a^x)’ = \ln(a)·a^x*$ ($*(a^x)’*$ est la dérivée de $*a^x*$)

Fonction réciproque

La fonction réciproque de $*a^x*$ est $*\log_a (x)*$ de sorte que $*\log_a (a^x) = a^{\log_a (x)} = x*$.

Comme je l’ai dit dans le paragraphe précédent, les fonctions logartihmes sont les fonctions réciproques des fonctions exponentielles. Donc il faudrait, si on voulait toujours être rigoureux, préciser la base $*a*$ du logartihme. Mais on fonctionne souvent, en physique du moins, par sous entendu. J’y reviens un peu plus tard.

Les fonctions logarithme sont :

• continues, dérivables et strictement monotones sur tout $*\mathbb{R}_+^* *$
• donc bijectives de $*\mathbb{R}_+^* \mapsto \mathbb{R}*$
• Décroissantes si leur base $*a*$ est telle que $*0 \lt a \lt 1*$
• Croissantes si leur base $*a*$ est telle que $* a \gt 1*$ (ce qui sera toujours le cas en physique).

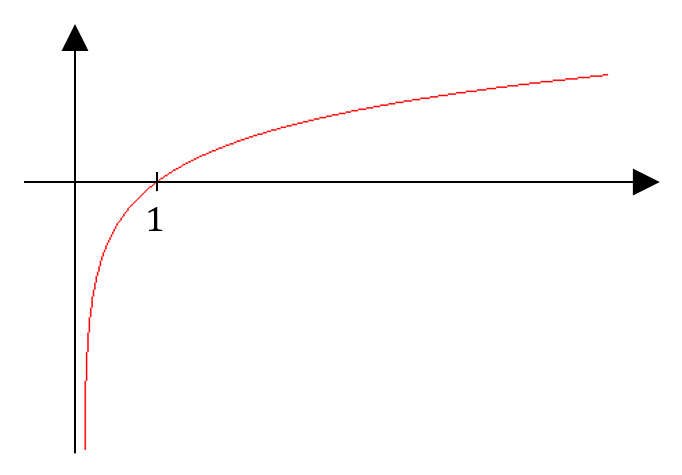
La fonction logarithme népérien

Elle est définie comme étant la primitive de la fonction $*\frac 1x*$ valant 0 pour $*x*$ = 1. Elle est notée $*\ln(x)*$. Sa réciproque est la fonction exponentielle de base $*\mathrm{e}*$, notée $*e^x*$ ou encore $*\exp(x)*$ ou $*\mathrm{e}*$ est un nombre irrationnel dont la valeur approchée est 2,71828.

La fonction logarithme décimale

Très utilisée en physique, c’est la réciproque de $*10^x*$. On devrait l’écrire $*\log_{10}(x)*$ mais on la note souvent $*\log(x)*$ tout simplement.
Si vous faites de la physique et de l’informatique, ça peut prêter à confusion, car les informaticiens – tout binaires qu’ils sont 😊 – utilisent cette notation pour parler de la fonction $*\log_2(x)*$.

Quelques propriétés

La notation $*\log_a(x)*$ désigne ici une fonction logarithme de base quelconque.

• $*\log_a(xy) = \log_a(x) + \log_a(y)*$

• $*\log_a(x^y) = y\log_a(x)*$

• $*\log_a(\frac xy) = \log_a(x) - \log_a(y)*$

• $*\log_a(x) = b \Leftrightarrow x = a^b *$ (très utile pour résoudre une équation)

• $*\log_a(x) = \log_a(y) \Leftrightarrow x = y*$ (très utile pour résoudre une équation)

• $*(\log_a(x))’ = \dfrac 1{x\ln(a)}*$ ($*(\log_a(x))’*$ est la dérivée de $*\log_a(x)*$)