Dimensions & unités
Une grandeur physique est une quantité qui se rapporte à une propriété et qui peut se mesurer. Mesurer, c’est comparer, à l’aide d'un instrument, une grandeur physique inconnue avec une grandeur de même nature — de même dimension — prise comme référence.
Dimensions (Tale)
En général, le résultat d'une mesure dépend de la référence utilisée. Par exemple, si l'on compare la longueur $*\ell*$ d'une règle de 1 m en prenant comme référence le centimètre, on obtient $*\ell*$ = 100 cm. Si la référence est le pouce, on trouvera $*\ell*$ ≃ 39,37 pouces.
La mesure est donc différente (100 ≠ 39,37) : on dit que la longueur possède une dimension.
L’unité d’une grandeur est purement conventionnelle (il existe des dizaines d’unités de longueur), mais sa dimension est indépendante de tout système d’unités (une longueur est une longueur, et n’a rien à voir avec une masse)
Si deux grandeurs ont la même dimension, on peut les comparer, les additionner, les soustraires…
Grandeur sans dimension
Mais il y a également des grandeurs physiques sans dimension. Dans ce cas la dimension est noté [G]=1.
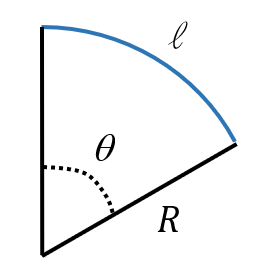
Ce sont les grandeurs qui représentent un rapport. La densité, par exemple, est une grandeur sans dimension – contrairement à la masse volumique. Les angles également (eh oui !), car un angle (en radian) n’est rien d’autre que le rapport entre la longueur de l’arc de cercle correspondant à cette angle, divisée par le rayon de ce cercle.
Les 7 dimensions de base
Ce sont les dimensions associées aux septs unités fondamentales dans le système S.I.
| Dimension | Symbole |
|---|---|
| Longueur | L |
| Masse | M |
| Temps | T |
| Intensité électrique | I |
| Température | Θ |
| Quantité de matière | N |
| Intensité lumineuse | J |
Équations aux dimensions
Une égalité entre deux grandeurs n’a de sens que si ces deux grandeurs ont la même dimension. Dire que 1,5 m = 12 kg est absurde. 😅
D’ailleurs, vous le savez depuis le primaire : votre maîtresse (ou votre maître) vous a toujours dit qu’on n’additionne pas des choux et de carottes.
Une équation aux dimensions permet ou bien de vérifier la pertinence, en terme de dimension, d’une relation donnée, ou bien de trouver la dimension d’une grandeur.
Un temps $*t*$ à une dimension… ben oui, d’un temps. [$*t*$] = T
Donc (et c’est là que ça devient intéressant) on peut en déduire les dimensions d’une vitesse. Puisqu’une vitesse (moyenne) est une distance parcourue pendant un certain temps : $µ v = \frac dt \Rightarrow [v] = \mathrm{LT}^{-1} µ$ De la même manière, la dimension d’une accélération $*a*$ est $µ [a] = \mathrm{LT}^{-2} µ$
Vérifier une formule
Une loi physique impose une contrainte qui n’existe pas en mathématique : elle doit être homogène, c'est-à-dire constituée de termes de même dimension.
Mais attention, ce n’est pas parce qu’elle est homogène qu’elle est nécessairement juste… 😊
Tout ce qu’on peut en dire, c’est qu’elle n’est pas absurde.
Dimensions de quelques grandeurs usuelles
1. Donner les dimensions des grandeurs suivantes :
a. force
b. pression
c. énergie
d. charge électrique
e. tension (rappelez-vous que l’énergie potientielle électrique $*E*$ d’une charge $*q*$ placée à un potentiel électrique $*V*$ en volt vaut $*E = qV*$.)
2. Montrer que la 3e loi de Kepler est homogène.
Correction
Vérification d’une relation
La période $*T*$ d’un pendule dépend de l’intensité $*g*$ du champ de pesanteur et de la longueur $*\ell*$ du fil.
Parmi les 4 relations ci-dessous, indiquer celle qui pourrait relier ces trois grandeurs :
Correction
Dimensions et fonctions
L’argument d’une fonction $*\cos*$, $*\sin*$, $*\exp*$ et $*\ln*$ est nécessairement sans dimension !
Ce n’est pas exactement ce qu’on a vu. on a vu que $µ \mathrm{pH} = -\log \left( { \ce{[H3O+]} \over c^\mathrm{o}} \right) µ$ avec justement $*c^\mathrm{o}*$, la concentration standard, qui vaut 1 mol·L-1. Le but de ce $*c^\mathrm{o}*$ est de faire en sorte que l’argument de la fonction logarithme soit sans dimension. Mais comme sa valeur vaut 1 mol·L-1, on est tenté de ne pas l’écrire. Il ne faut cependant pas oublier sa présence.
Unités
Les unités fondamentales
Il y a 7 unités fondamentales dans le système SI, qui sont indépendante du point de vu dimensionnel.
Depuis le 20 mai 2019, les unités du SI sont définies à partir de sept constantes de la nature auxquelles on donne une valeur fixe (c’est-à-dire avec une précision infinie).
| Dimension | Symbole | Unité | Symbole |
|---|---|---|---|
| Longueur | L | mètre | m |
| Masse | M | kilogramme | kg |
| Temps | T | seconde | s |
| Intensité électrique | I | ampère | A |
| Température | Θ | kelvin | K |
| Quantité de matière | N | mole | mol |
| Intensité lumineuse | J | candela | cd |
Toutes les autres unités du système SI (newton, pascal, tesla, volt, watt, joule) dérivent de ces 7 unités de bases.
Décomposition d’unités
Décomposer les unités suivantes en leu expression en fonction des unités fondamentales : newton, pascal, volt, watt, joule
Correction
Calculs avec des unités
Les unités se traitent dans les calculs comme des expressions littérales. Cela vous permet de convertir très facilement des unités.
Exemples
• 2,5 m2 = 2,5×(100 cm)2 = 2,5×1002 cm2 = 2,5·104 cm2
• 0,5 miles·min-1 = 0,5×(1609 m)·(60 s)-1 = 0,5×1609÷60 m·s-1 = 13,41 m·s-1
Quelques unités usuelles
À savoir dès le collège
- 1 m3 = 1000 L
- 1 cm3 = 1 mL
- 1 m/s = 3,6 km/h
- 1 t (tonne) = 1000 kg
Autres unités usuelles (à savoir dès la première)
- 1 bar = 105 Pa
- 1 eV = 1,602·10-19 J
- 1 W·h = 3600 J
Unité de conductivité
L’unité SI de la conductivité est le siemens par mètre (S·m-1).
Mais les conductimètres affichent souvent la mesure en mS·cm-1.
Trouver le facteur de conversion.
Correction
Multiples & sous-multiples
Les multiples (kilo, méga…) et sous-multplies (milli, micro…) sont plus faciles à lire, à écrire et à dire que les puissances de 10 correspondantes. Je les utilise donc largement dans mes cours. Vous devez donc savoir les multiples et sous-multiples ci-dessous par cœur, y compris au collège.
Multiples
| nom | symbole | puissance de 10 |
|---|---|---|
| kilo | k | 103 |
| méga | M | 106 |
| giga | G | 109 |
Sous-multiples
| nom | symbole | puissance de 10 |
|---|---|---|
| milli | m | 10-3 |
| micro | µ | 10-6 |
| nano | n | 10-9 |