À propos des vecteurs
Coordonnées
Il est souvent nécessaire de trouver les coordonnées d’un vecteur, connaissant sa norme et l’angle qu’il fait avec un des axes du repère.
✋ À garder en mémoire définitivement :
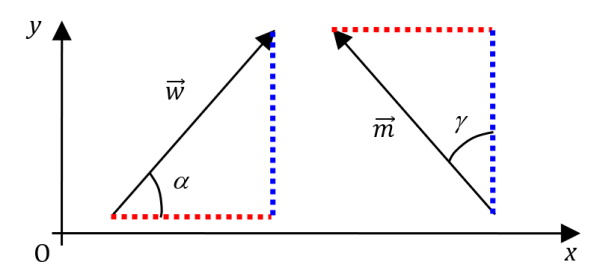
$µ \vec{w} \begin{pmatrix} \begin{aligned} w_x &= w·\cos \alpha \\ w_y &= w·\sin \alpha \\ \end{aligned} \end{pmatrix} \quad \vec{m} \begin{pmatrix} \begin{aligned} m_x &= -m·\sin \gamma \\ m_y &= m·\cos \gamma \\ \end{aligned} \end{pmatrix} µ$
Faites attention au signe des coordonnées.
Allez, entraînez-vous avec ces vecteurs :
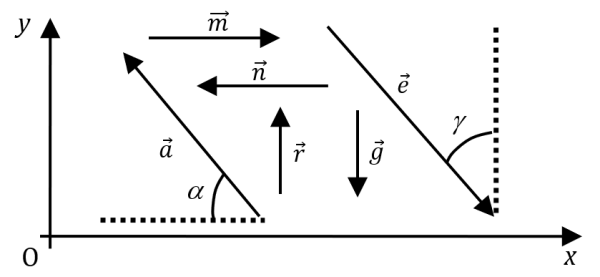
Réponses
$µ \vec{m} \begin{pmatrix} \begin{aligned} m_x &= m \\ m_y &= 0 \\ \end{aligned} \end{pmatrix} \quad \vec{n} \begin{pmatrix} \begin{aligned} n_x &= -n \\ n_y &= 0 \\ \end{aligned} \end{pmatrix} µ$
$µ \vec{r} \begin{pmatrix} \begin{aligned} r_x &= 0 \\ r_y &= r \\ \end{aligned} \end{pmatrix} \quad \vec{g} \begin{pmatrix} \begin{aligned} g_x &= 0 \\ g_y &= -g \\ \end{aligned} \end{pmatrix} µ$
$µ \vec{a} \begin{pmatrix} \begin{aligned} a_x &= -a·\cos \alpha \\ a_y &= a·\sin \alpha \\ \end{aligned} \end{pmatrix} \quad \vec{e} \begin{pmatrix} \begin{aligned} e_x &= e·\sin \gamma \\ e_y &= -e·\cos \gamma \\ \end{aligned} \end{pmatrix} µ$
Additionner et soustraire des vecteurs
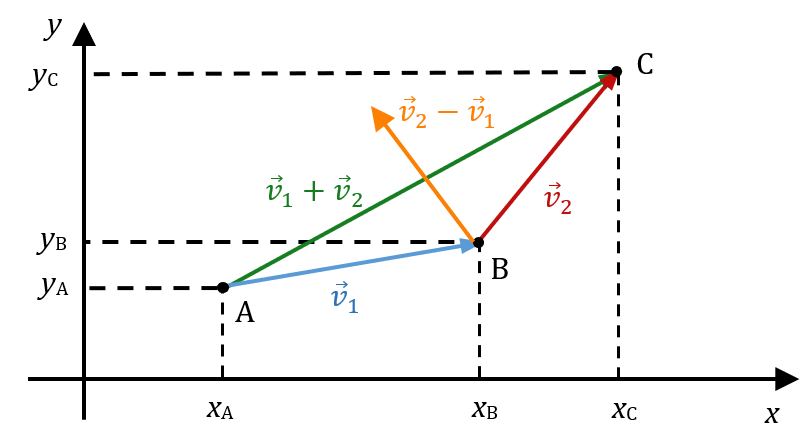
Coordonnées du vecteur $*\vec{v}_1*$ : ($*x_B \; – x_A*$ ; $*y_B \; – y_A*$) notées ($*x_1*$ ; $*y_1*$)
Coordonnées de vecteur $*\vec{v}_2*$ : ($*x_C \; – x_B*$ ; $*y_C \; – y_B*$) notées ($*x_2*$ ; $*y_2*$)
Coordonnées du vecteur $*\vec{v}_1 + \vec{v}_2*$ : ($*x_1 + x_2*$ ; $*y_1 + y_2*$)
Coordonnées du vecteur $*\vec{v}_2 - \vec{v}_1*$ : ($*x_2 - x_1*$ ; $*y_2 - y_1*$)