1.1 Éléments chimiques & radioactivité
Les éléments chimiques
- Produire et analyser différentes représentations graphiques de l’abondance des éléments chimiques (proportions) dans l’Univers, la Terre, les êtres vivants.
Il existe, à l’état naturel, environ 90 « types » d’atomes différents. Par exemple, il y a les atomes d’hydrogène, de carbone, de fer, etc...
Ces différents types d’atomes sont appelés des éléments chimiques.
Quelques définitions
Corps composé : substance composée de différentes types de molécules et/ou d’ions (exemples : l’air, l’eau de mer, les roches, ...)
Corps pur : substance composée d’un seul type de molécule ou d’un seul couple anion/cation (exemples : l’eau, le chlorure de sodium $*\ce{NaCl}*$, le glucose $*\ce{C6H12O6}*$ …)
Corps simple: corps pur composé d’un seul type d’atome (le dioxygène $*\ce{O2}*$, l’ozone $*\ce{O3}*$, le dihydrogène $*\ce{H2}*$ …)
Nombre de masse $*A*$ : nombre de nucléons (protons + neutrons) que comporte un noyau.
Numéro atomique $*Z*$ : nombre protons que comporte un noyau, ce nombre définit à quel élément chimique appartient le noyau.
La notation $*^A_Z\ce{X} *$, où $*\ce{X}*$ est le symbole chimique de l’élément, permet d’expliciter la composition d’un noyau.
Le tableau périodique dresse une liste organisée de tous les éléments chimiques connus à ce jour.
Eh bien non ! Et comment peut-on en être sûr ? La réponse est simple. Vous avez vu l’année dernière le tableau périodique et vous vous souvenez bien sûr que les éléments chimiques y sont classés par numéro atomique croissant. Dans ce classement, il n’y a aucun « trou ». On connaît tous les éléments chimiques jusqu’à des numéros atomiques supérieur à 92 (on en est actuellement à $*Z*$ = 118 !).
Si ! Et ils peuvent même exister sur Terre... On peut les créer en laboratoire grâce à des réactions nucléaires, mais ils ont presque tous une durée de vie brève, voire très brèves. Ils sont radioactifs. C’est pour ça que je précise qu’il existe environ 90 éléments « à l’état naturel ». Nous y reviendrons plus tard dans ce chapitre.
Abondance relative des différents éléments
Abondance relative, en nombre d’atomes, des éléments les plus abondants dans :
| Univers | Litosphère | Le corps humain |
|---|---|---|
| H : 90 % | O : 47,7 % | H : 61 % |
| He : 9 % | Si : 27,7 % | O : 24,1 % |
| Autres : 1 % | Al : 8,2 % | C : 12,6 % |
| Fe : 4,1 % | N : 1,4 % | |
| Ca : 4,1 % | Autres : 0,9 % | |
| Na : 2,3 % | ||
| Mg : 2,3 | ||
| K : 2,1 % | ||
| Autres : 1,5 % |
Représenter sur un diagramme en camembert, (avec un tableur, pas à la main… 😉) l’abondance des différents éléments dans l’Univers, la litosphère et le corps humain. Représenter la part de l’hydrogène en gris clair et la part de l’oxygène en rouge.
Correction
Voici le fichier obtenu.
La nucléosynthèse
- L’équation d’une réaction nucléaire étant fournie, reconnaître si celle-ci relève d’une fusion ou d’une fission.
D’où viennent les atomes de l’Univers ? Par quel mécanisme se sont-ils formés ?
Nucléosynthèse primordiale
Lors des 3 première minutes après le Big Bang, l’Univers était tellement chaud que la fusion des noyaux d’hydrogène était possible. Ces réactions de fusion, que l’on appelle la nucléosynthèse primordiale, ont produit de l’hélium ($*Z*$ = 2) et un peu de lithium ($*Z*$ = 3). Après ces 3 premières minutes, l’Univers était déjà trop « froid » pour que ces réactions de fusion se poursuivent.
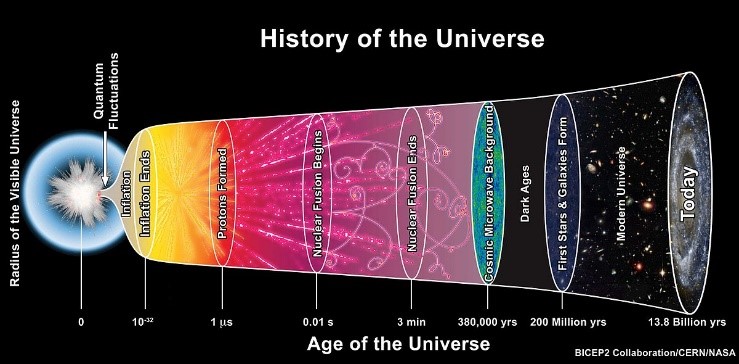
Nucléosynthèse stellaire
Environ 100 millions d’années après le Big Bang se forment les premières étoiles.
Séquence principale d’une étoile
Au cours de la séquence principale de la vie d’une étoile, les noyaux d’hydrogène de son cœur (dont la température est de plusieurs millions de kelvins, et où la pression est extrêmement élevée) fusionnent pour donner de l’hélium 4 selon une réaction de fusion nucléaire dont le bilan est :
$µ \ce{ 4 ^1_1H + 2 e^-} \rightarrow \ce{^4_2He } µ$
Ce processus de fusion (association de noyaux légers pour donner un noyau plus lourd avec éventuellement le rejet d’une particule légère) dégage beaucoup d’énergie lorsque ce sont des noyaux d’hydrogène qui fusionnent.
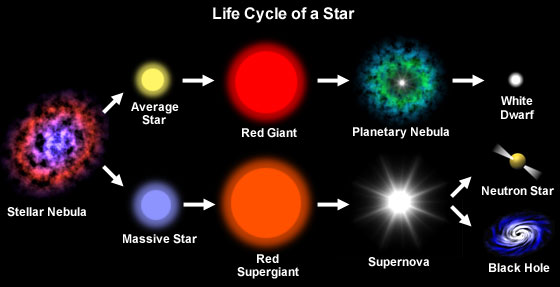
Les autres éléments ne sont produits que lors de la fin de la vie d’une étoile.
Fin de vie d’une étoile
En fin de vie, l’étoile a « brûlé » tout son hydrogène et son cœur contient essentiellement de l’hélium. Commencent alors d’autres réactions de fusion et de fission qui produisent des éléments plus lourds (oxygène, carbone…).
En voici quelques exemples :
$µ \begin{aligned} \ce{^4_2He + ^4_2He} &\rightarrow \ce{^8_4Be} \\ \ce{^4_2He + ^8_4Be} &\rightarrow \ce{^12_6C} \\ \ce{^12_6C + ^4_2He} &\rightarrow \ce{^16_8O} \end{aligned} µ$
La fission nucléaire forme de nouveaux noyaux atomiques (et donc de nouveaux éléments) en « cassant » un noyau grâce à l’impact d’une particule (proton, neutron…). En plus des deux noyaux plus petits, créés par fission du noyau originel, il peut également y avoir d’autres petites particules produites (neutrons ou protons). Voyez l’équation de fission de l’uranium 235 dont je parle dans l’encadré à droite (ou un peu plus bas si vous lisez ce cours sur votre téléphone).
Par exemple, certaines étoiles en fin de vie fabrique du carbone à partir d’azote 15 qui a été produit par fusion nucléaire. La fission de l’azote 15 par collision avec un proton produit du carbone 12, selon la réaction :
$µ \ce{^15_7N + ^1_1H} \rightarrow \ce{^12_6C + ^4_2He} µ$
La fission est par contre largement utilisée par l’Homme dans les centrales nuclaires, qui utilisent la fission de l’uranium 238 : $µ \ce{^235_92U + ^1_0n \rightarrow X + Y + \mathit{k}\;^1_0n} µ$ où $*\ce{X}*$ et $*\ce{Y}*$ représentent deux noyaux plus petits et $*\ce{^1_0n}*$ représente un neutron.
L’élément le plus lourd produit au cours de cette phase est le fer (et encore, seulement pour les plus grosses étoiles). Ces réactions nucléaires produisent moins d’énergie que la fusion de l’hydrogène. L’étoile change alors de taille (elle commence à enfler) et de température (elle se refroidit et sa couleur va donc évoluer vers le rouge).
Les étoiles les plus massives (plus de 8 masses solaires) explosent en supernovæ. Au cours de cet événement extrêmement violent, les noyaux les plus lourds de l’Univers (ceux qui sont plus lourds que le fer) sont formés par des réactions nucléaires complexes et mal connues. La formation de noyaux plus lourd que le fer consomment de l’énergie.
Fusion : association de deux noyaux pour former un noyau plus lourd, avec éventuellement rejet d’une particule légère (neutron ou proton).
Fission : cassure d’un noyau pour sous l’effet d’un impacteur (neutron ou proton) pour former deux noyaux plus légers. Les noyux produits ont des tailles comparables.
Réactions nucléaires
Identifier, parmi les réactions suivantes, celles qui relèvent d’une fusion ou d’une fission en justifiant :
1. $*\ce{_92^235U + _0^1n \rightarrow \ _54^139 Xe + _38^94 Sr + 3 _0^1n }*$
2. $*\ce{_1^2H + _1^2H \rightarrow \ _1^3H + _1^1H }*$
3. $*\ce{ _3^7Li + _2^4He \rightarrow \ _5^10B + _0^1n }*$
4. $*\ce{ _83^210Bi \rightarrow \ _84^210Po + e^- }*$
5. $*\ce{ _7^14N + _1^1H \rightarrow \ _8^15O + γ }*$
6. $*\ce{ _88^226Ra \rightarrow \ _86^222Rn + _2^4He }*$
Correction
1. Fission : un noyau initial, un particule (neutron), puis deux noyaux plus petits.
2. Fusion : deux noyaux forment un noyau plus lourd.
3. Fusion
4. Ni fission, ni fusion
5. Fusion
6. Ni fission, ni fusion
La radioactivité
- Calculer le nombre de noyaux restants au bout de n demi-vies.
- Estimer la durée nécessaire pour obtenir une certaine proportion de noyaux restants.
- Utiliser une représentation graphique pour déterminer une demi-vie.
- Utiliser une décroissance radioactive pour une datation (exemple du carbone 14).
Activité : décroissance radioactive
Objectif : découvrir la loi de décroissance d’une population de noyaux radioactifs.
Quelques fonctions d’Excel
ALEA.ENTRE.BORNES(min ; max) : renvoie un nombre entier aléatoire compris entre min (inclus) et max (inclus).
SI(condition ; formule 1 ; formule 2) : applique la formule 1 si la condition est vérifiée, ou la formule 2 si la condition n’est pas vérifiée.
- Tester la fonction
ALEA.ENTRE.BORNESsur Excel. La touche F9 (ou Fn + F9) permet de refaire les tirages aléatoires. - Écrire une formule dans B1 qui affiche « 0 » si la case A1 contient 0 et « non » si la case A1 contient autre chose que 0.
Application : s’il n’en reste qu’un…
- Dans la case A2, entrer
=1. - Dans la case B2, écrire une formule qui va faire en sorte que si A2 = 0, alors B2 = 0, sinon B2 aura 50 % de chance de prendre la valeur 1 et 50 % de chance de prendre la valeur 0.
- Répéter l’opération pour la case C2 qui dépendra de la case B2, puis pour D2 qui dépendra de la case C2, ainsi de suite jusqu’à la colonne O.
- Répéter la même opération pour avoir 1000 lignes identiques (de la ligne 2 à la ligne 1001).
- Dans la case A1, faites la somme des cases A2 à A1001, idem pour B1, C1, etc. jusqu’à O1.
Questions
- Que constate-t-on ?
- Si la somme des cases d’une colonne est égale à 128, de quelle colonne s’agit-il probablement ?
- Si la somme d’une colonne est égale à 1, peut-on savoir de quelle colonne il s’agit ?
Graphique
- Représenter sur un graphique la somme des colonnes de A à O en fonction du numéro de colonne.
- Appuyez sur la touche F9 pour refaire les tirages aléatoires. Que constate-t-on ?
Certains noyaux sont instables et se « désintègrent » : on dit qu’ils sont radioactifs. En fait, ils ne disparaissent pas, mais se transforment spontanément en un autre noyau selon des réactions qui ne seront pas étudiées dans ce cours.
L’instant de désintégration d’un noyau radioactif individuel est aléatoire.
Eh bien on ne peut pas prévoir quand le noyau se « désintegrera ». Mais, si on connaît la demi-vie du noyau (qui dépend de sa nature), on peut calculer la probabilité que ce noyau a de se désintégrer dans les x prochaines minutes / semaine / années / etc. Comme on l’a vu dans l’activité au début de ce paragraphe, on peut faire des prévisions fiables lorsqu’on dispose d’une grande quantité de noyaux.
La demi-vie d’un noyau radioactif est la durée nécessaire pour que la moitié des noyaux initialement présents dans un échantillon macroscopique se soit désintégrée. Cette demi-vie est caractéristique du noyau radioactif : elle dépend de son numéro atomique et de son nombre de masse.
Population de noyaux radioactifs
L’uranium 238 $*\ce{^238U}*$ est l’isotope le plus courant de l’uranium sur Terre (99,3 % de l’uranium naturel). Sa demi-vie est d’environ 4,5 milliards d’années.
1. Quel pourcentage de l’uranium 238 initialement présent lors de la formation de la Terre reste-t-il de nos jours ?
2. Qu’en sera-t-il à la fin du système solaire, dans environ 4,5 milliard d’années ?
Correction
1. La Terre a environ 4,5 milliards d’années, ce qui correspond à la demi-vie de $*\ce{^238U}*$. Donc il reste de nos jours environ 50 % de la quantité initiale d’uranium 238.
2. Il restera 50 % de la quantité actuelle, soit 25 % de la quantité présente au moment de la formation de la Terre.
Déterminer une demi-vie
Le graphique ci-dessous montre le nombre de désintégrations d’un échantillon de noyaux radioactifs en fonction du temps. Ce nombre de désintégrations est proportionnel à la quantité de noyaux radioactifs que contient l’échantillon.
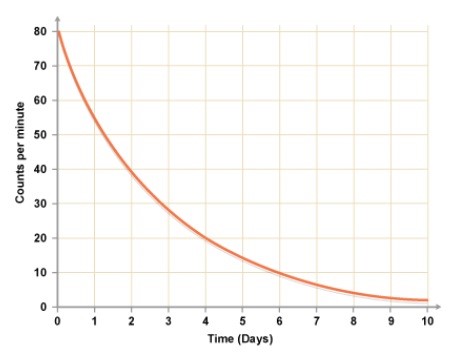
Quelle est la demi-vie de ces noyaux ?
Correction
On voit que le nombre de désintégration a été divisé par deux au bout de 2 jours. Donc la demi-vie est de deux jours.Datation au carbone 14
Des archéologues souhaitent dater un manche de lance. Des mesures de désintégration sont faites et on obtient 9,2 désintégrations par minute et par gramme.
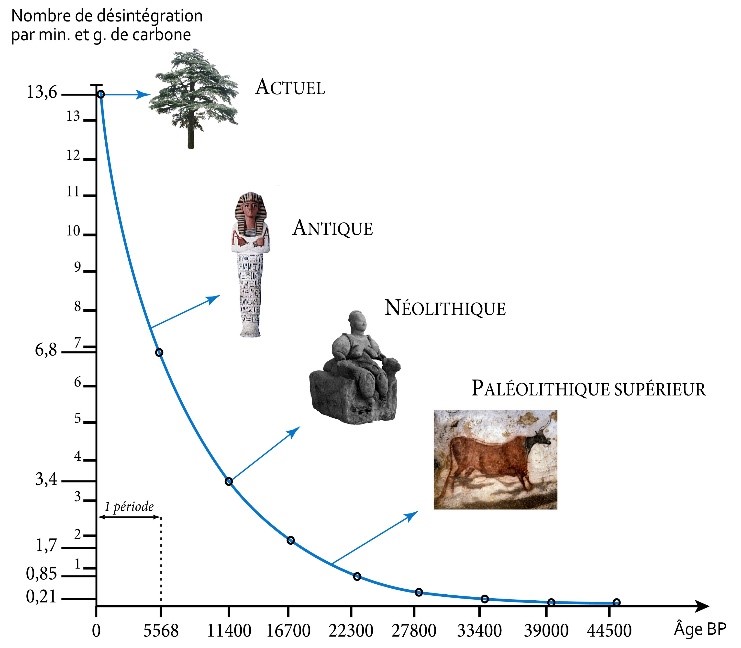
1. Quel est l’âge approximatif de ce manche de lance ?
2. Quel problème se pose si on réalise des mesures sur un échantillon de très faible masse ?
3. Lucy, le squelette d’australopithèque découvert en 1974, a été daté d’environ 3,2 millions d’années. Cette datation a-t-elle pu être faite grâce au carbone 14 ?
Correction
1. Par lecture graphique, ça fait environ 2800 ans.
2. Le nombre d’atomes de $*\ce{^14C}*$ est trop faible pour que le résultat de la mesure soit fiable. On ne se trouve plus dans une situation où la loi des grands nombres peut s’appliquer, le caractère aléatoire de la désintégration devient trop important pour permettre des prédiction statistiques fiables.
3. Non car les restes sont tellement vieux qu’ils ne contiennent plus de $*\ce{^14C}*$.
Révision & entraînement
Fission ou fusion ?
1. $*\ce{_94^239Pu + \ _0^1n \rightarrow \ _54^134Xe + _40^103Zr + 3 \ _0^1n}*$
2. $*\ce{_1^3H \rightarrow \ _2^3He + _{-1}^0e^-}*$
3. $*\ce{_1^2H + _1^3H \rightarrow \ _2^4He + _0^1n}*$
4.$*\ce{_92^235U + _0^1n \rightarrow \ _62^154Sm + _30^79Zn + 3 _0^1n}*$
Correction
1. Fission
2. Ni fission, ni fusion
3. Fusion
4. Fission
Datation au carbone 14
Le graphique ci-dessous représente le rapport $*P/P_0*$ du nombre d’atomes $*\ce{^14C}*$ résiduels sur le nombre d’atomes $*\ce{^14C}*$ présent au moment de la mort en fonction du nombre d’années écoulées depuis la mort. L’encart-zoom permet de mieux visualiser la période entre 20 000 et 40 000 ans.
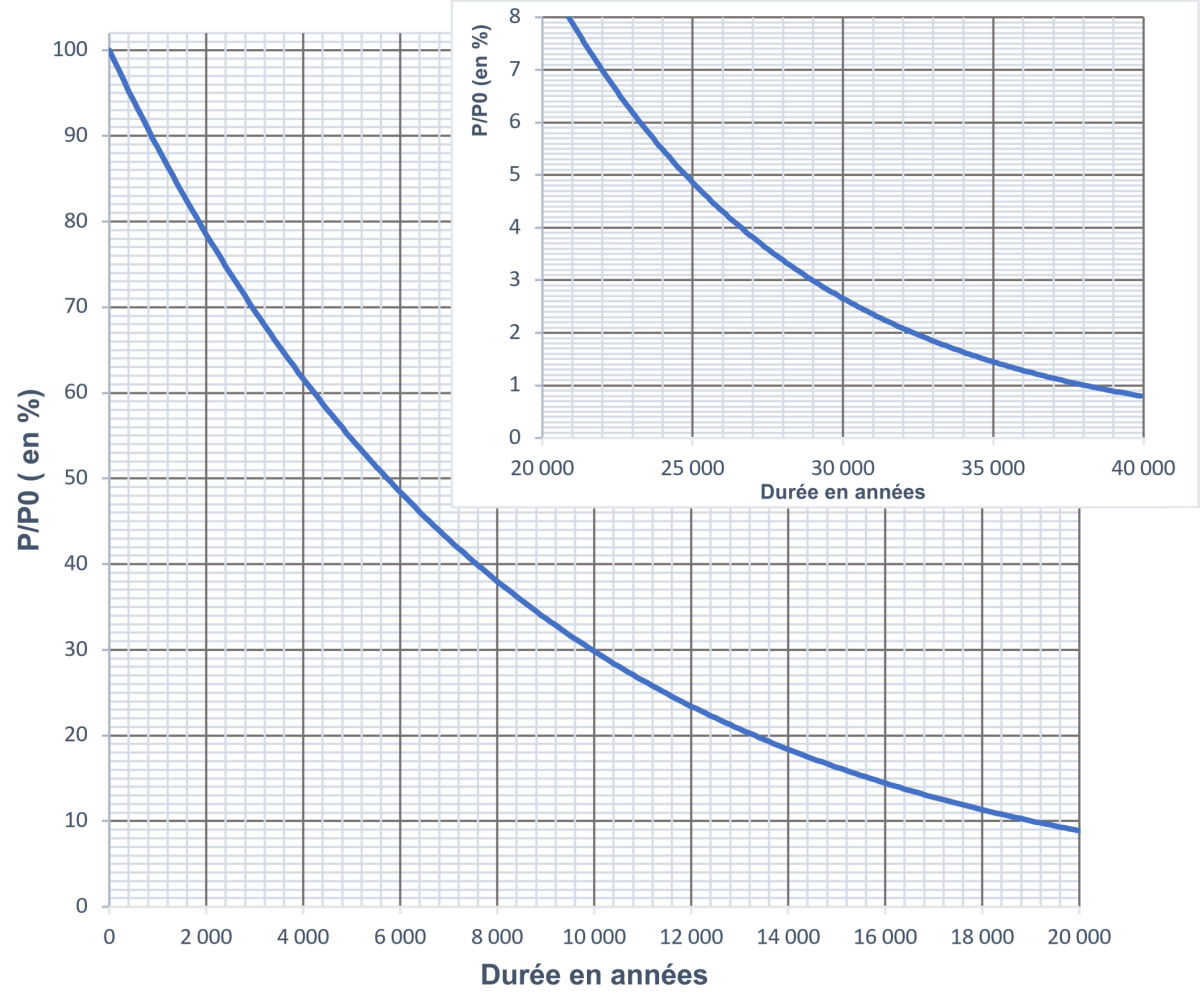
1. En exploitant le graphique, estimer, après l’avoir définie, la demi-vie du carbone 14.
2. Des morceaux de charbon ont été retrouvés à l’entrée d’une grotte. Leur rapport $*P/P_0*$ est compris entre 6,5 et 5,5 %. Estimer par un encadrement l’ancienneté des traces de l’habitation de cette grotte.
Correction
1. Demi-vie : temps au bout duquel la moitié des noyaux d’un isotope radioactif se sont désintégrés.
Par lecture graphique : $*P/P_0*$ = 50 % après environ 5700 ans.
2. Ces traces datent de 22500 à 24000 ans environ.
Le polonium, un poison radioactif
Cet exercice est tiré d’une épreuve d’E3C
Le polonium-210 ($*^{210}\ce{Po}*$) est un élément radioactif et un poison très puissant utilisé par certains services secrets. Dix microgrammes (µg) suffisent à empoisonner un homme de poids moyen en quelques semaines et cette dose mortelle est invisible à l’œil nu.
Son utilisation est cependant réservée à une organisation disposant de moyens importants, puisque sa production nécessite un réacteur nucléaire.
Un agent secret se voit remettre 15 µg de polonium afin d’empoisonner une cible. L’objectif de l’exercice est de déterminer le temps dont dispose l’agent pour mener à bien sa mission.
Données
- Masse molaire du polonium : M(Po) = 210 g∙mol-1
- Nombre d’Avogadro $*N_A*$ = 6,02·1023 mol-1
1. Déterminer la masse initiale, en µg, de polonium présente dans l’échantillon utilisé pour réaliser le graphique ci-dessous.
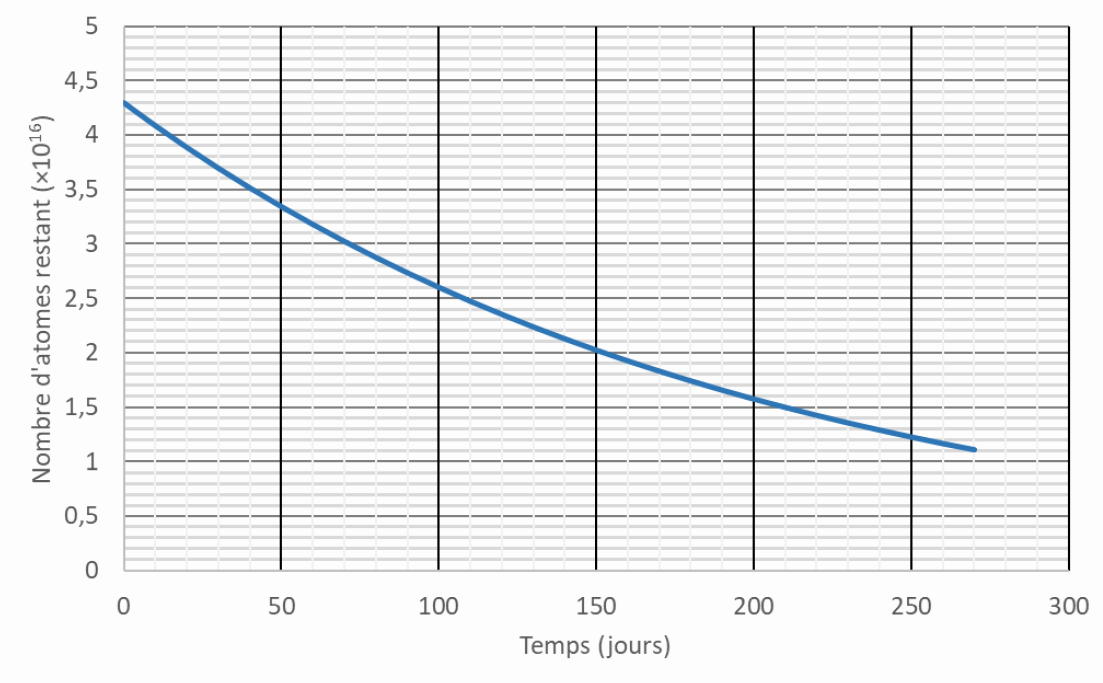
2.a. Donner la définition de la demi-vie d’un élément radioactif.
2.b. La faire figurer sur le graphique de l’énoncé en laissant apparents les traits de construction.
3. De combien de temps dispose l’espion pour réussir sa mission ?
Correction
1. Il faut d’abord calculer la masse d’un atome : il suffit de diviser la masse d’une mole (210 g) par le nombre d’atomes qu’il y a dans une mole (c’est-à-dire le nombre d’Avogadro $*N_A*$) : 210÷6,02·1023 = 3,488·10-22 g
Puis on peut en déduire la masse de l’échantillon en connaissance le nombre d’atomes qu’il contient (par lecture graphique : 4,3·1016 noyaux) :
3,488·10-22×4,3·1016 = 1,5·10-5 g = 15 µg
2.a. Demi-vie d’un isotope radioactif : durée nécessaire à la désintégration de la moitié des noyaux de cet isotope.
2.b. Détermination graphique de la demi-vie.
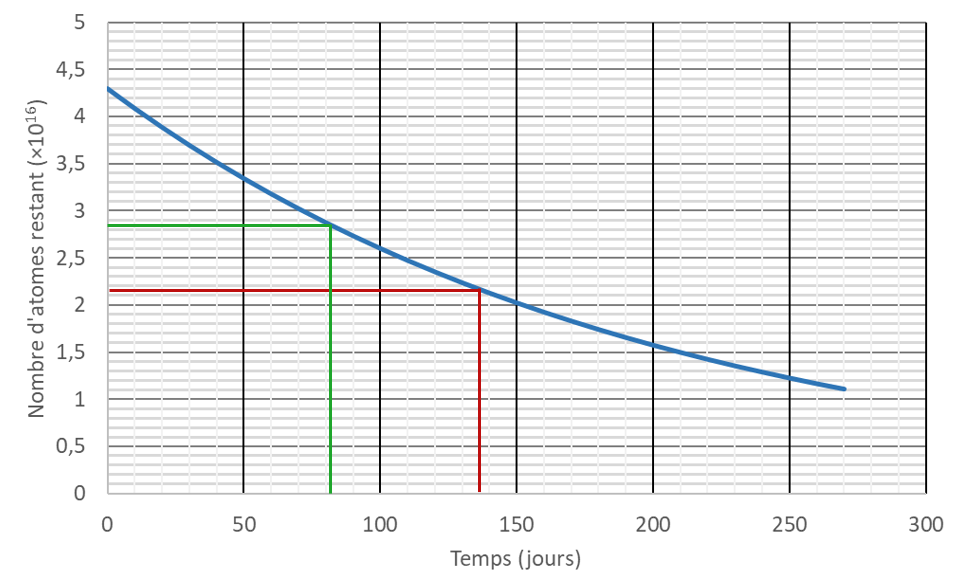
3. Pour réussir la mission, il faut 10 µg, soit les ⅔ de la masse initiale, soit environ 2,85·1016 noyaux (soit les ⅔ des 4,3·1016 noyaux initiaux). Par lecture graphique (en vert), on trouve environ 80 jours.