1.2 Les cristaux
Dans le précédent chapitre, on a vu un niveau d’organisation de la matière : les éléments chimiques. Toutes la matière qui nous entoure est constituée exclusivement de quelques dizaines d’éléments chimiques différents. On va voir dans ce chapitre un autre niveau d’organisation : les cristaux.
Les cristaux ont une grande importance en physique et en chimie, car beaucoup de solides sont des cristaux.
Le chlorure de sodium
- Utiliser une représentation 3D informatisée du cristal de chlorure de sodium.
- Relier l’organisation de la maille au niveau microscopique à la structure du cristal au niveau macroscopique.
Le chlorure de sodium, à l’état solide, est un exemple de cristal. Pourquoi parler du chlorure de sodium $*\ce{NaCl}*$ en particulier ? Tout simplement parce que c’est un cristal que l’on rencontre tous les jours : c’est du sel de cuisine.

Le chlorure de sodium en solution n’a bien sûr pas du tout la même organisation, puisque les ions sont dissous dans l’eau.
Dans du chlorure de sodium à l’état solide, les ions $*\ce{Na+}*$ et $*\ce{Cl-}*$ sont empilés de manière régulière. C’est ce qu’on appelle l’état cristallin. En fait, beaucoup de substances, à l’état solide, ont une structure cristalline. Mais on en reparlera plus tard.
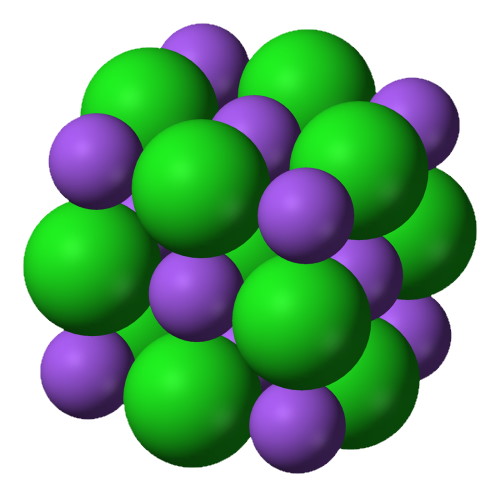
Cette structure microscopique est d’ailleurs responsable de la forme des cristaux à l’échelle macroscopique. Sur l’illustration ci-dessous, regardez les angles formés par les différentes faces du cristal : ils font 90°. Ceci s’explique par le fait dans le cristal de $*\ce{NaCl}*$, l’empilement des ions forment des cubes.


Non, bien-sûr ! Ça ne serait pas très pratique de saler votre assiette avec de gros cristaux de 1 cm3… 😄
Plus sérieusement, le sel de cuisine est généralement du sel obtenu par évaporation d’eau salée. Cette évaporation étant rapide, il ne se forme pas de gros cristaux comme celui de l’illustration, mais de nombreux cristaux plus petits. Et si vous les observez au microscope, vous verrez qu’ils possèdent ces mêmes angles de 90°.
Structure cristalline
- Pour des réseaux cubique simple et cubique à faces centrées :
- représenter la maille en perspective cavalière ;
- calculer la compacité dans le cas d’entités chimiques sphériques tangentes ;
- dénombrer les atomes par maille et calculer la masse volumique du cristal.
On va maintenant aborder des notions plus générales à propos des cristaux.
Un cristal, c’est un empilement ordonné d’ions (les cristaux ioniques, comme le $*\ce{NaCl}*$ qu’on vient de voir), d’atomes (les métaux à l’état solide ont une structure cristalline) ou de molécules (cristaux moléculaires – le sucre, par exemple). La manière dont les entités chimiques s’empilent dépendent de l’espèce chimique considérée, mais aussi des conditions de température et de pression.
Maille élémentaire
La maille élémentaire (ou plus simplement maille) d’un cristal, c’est le « motif de base » du cristal, grâce auquel on peut obtenir le cristal entier simplement par translation.
Autrement dit, par répétition de la maille, en les juxtaposant entre elles, on peut reproduire la structure complète d’un cristal.
Il existe 7 formes géométriques différentes de mailles, aussi appelés systèmes cristallins. On va en étudier qu’une seule, la plus simple, le cube.
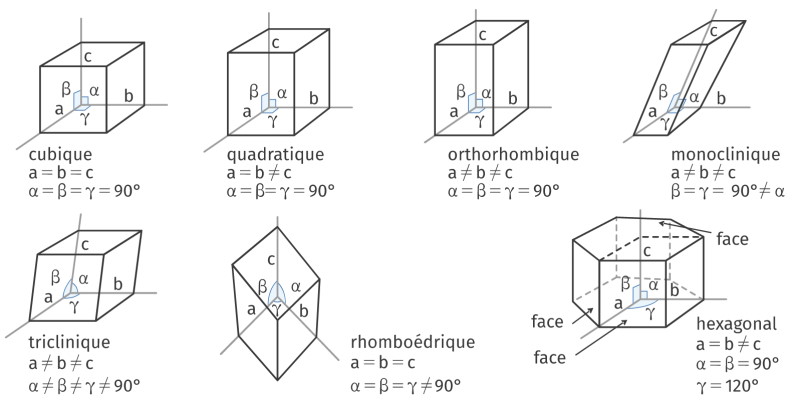
Il existe plusieurs structures de mailles cubiques : cubique simple, cubique à face centrée et cubique centrée.
La structure cubique simple
Voilà la structure cristalline la plus simple. Dans cette structure, les ions ou les atomes sont empilés de manière à se positionner aux 8 sommets d’un cube.
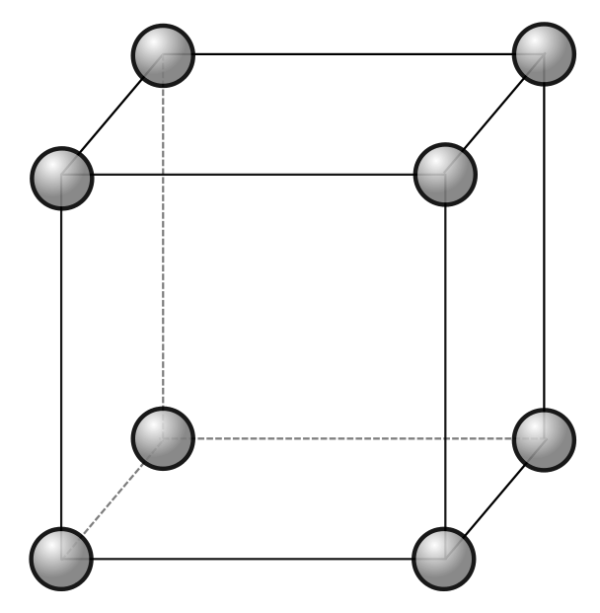
Cette maille n’est pas très répandue parmi les cristaux, car elle ne présente pas un empilement très compact. Si vous deviez mettre un maximum d’oranges dans une cagette, ce n’est certainement pas comme ça que vous les empileriez... 😉

La structure cubique à face centrée
Un petit peu plus compliqué. Dans ce type de maille, vous avez un atome ou un ion à chacun des 8 sommets du cube, ainsi qu’un atome ou un ion au centre de chaque face du cube.
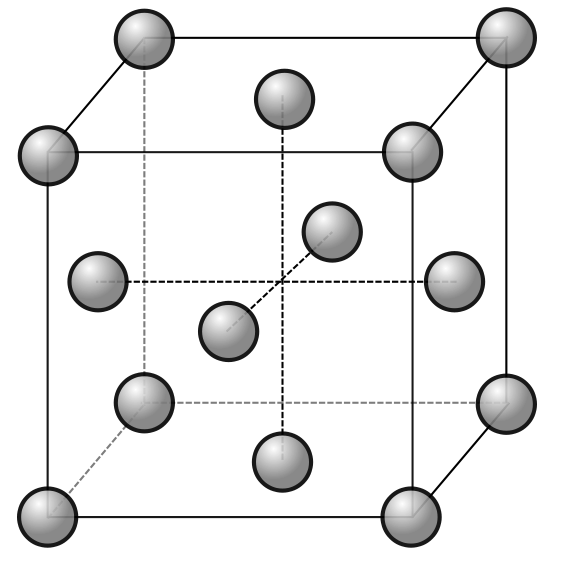
Nombre d’atomes par maille
Remarque : dans le paragraphe ci-dessous, lorsque je parle d’« atome », ça inclut aussi les ions. Je ne vais pas écrire à chaque fois « atome ou ion »...
Cubique simple (CS)
Combien d’atomes y a-t-il dans chaque maille CS ? 8 ?
Non, raté. 😊 Pour former deux mailles, vous n’avez pas besoin de 16 atomes, car certains atomes seront partagés entre les deux mailles. En fait, si vous imaginez un grand cristal et que vous visualisez une maille au centre, les atomes de cette maille seront tous partagés par 7 autres mailles.
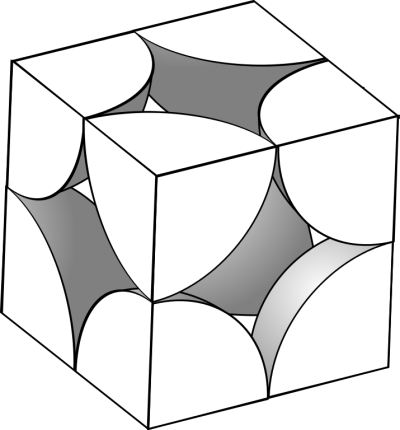
Donc en fait, chaque maille cubique simple possède en propre 8×⅛ = 1 atome !
Cubique à faces centrées (CFC)
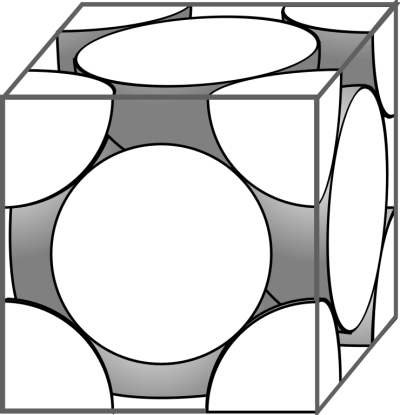
Maintenant que vous avez compris ce point délicat, déterminer le nombre d’atomes qui appartiennent en propre à une maille CFC est facile !
Pour les atomes situés aux sommets du cube, c’est le même principe. Donc ça fait 8×⅛. Par contre, les atomes situés sur les faces du cube ne sont partagés que par deux mailles. Il y a 6 faces, chacune comptant pour ½ donc ça fait 3. Ce qui nous amène à un total de 4 atomes par maille.
La maille cubique centrée
Voici un schéma montrant la maille cubique centrée
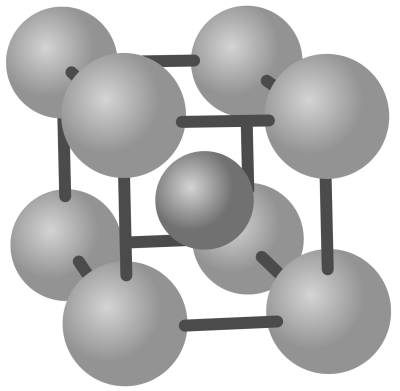
Combien comporte-t-elle d’atomes ?
Réponse
8×⅛ + 1 = 2
Compacité
Un peu de vocabulaire avant de commencer. L’arête d’une maille est appelée, en cristallographie, le paramètre de maille, souvent noté $*a*$. Retenez ce terme, nous nous en servirons régulièrement pour la suite du cours.
La compacité d’un empilement, c’est la proportion du volume occupé par les objets empilés par rapport au volume total occupé par l’empilement qui inclut donc les vides entre les objets.
Quand on empile des sphères, il reste un espace vide entre elles. Cet espace peut se calculer assez facilement si on connaît la taille des sphères et le type d’empilement.
Pour faire ce calcul, on assimile les atomes à des sphères non déformables, qui sont en contact les unes avec les autres. Attention ! Les schémas que je vous ai montrés plus haut représentent des vues « éclatées », c’est-à-dire qu’on a disjoint les atomes pour des raisons de lisibilité du schéma. Dans la réalité, un empilement cubique simple, ça ressemble plutôt à ça :

Pour calculer la compacité d’une maille cubique simple, rien de plus simple… 😊 Il faut bien-sûr connaître le rayon $*r*$ des atomes constituant le cristal et le paramètre de maille $*a*$.
Puisque, dans un telle structure, il y a un atome par maille, la compacité $*c*$ se calcule par la formule suivante : $µ \mathrm{compacité} = { \mathrm{volume\; 1 \; atome} \over \mathrm{volume \; maille} } µ$
Ou encore : $µ c = \frac 43 \frac {\pi r^3}{a^3} µ$
mais comme les atomes se touchent, on a $*a = 2r*$. Du coup : $µ \begin{aligned} c &= \frac 43 \frac {\pi r^3}{(2r)^3} \\ c &= \frac {\pi}6 \end{aligned} µ$
Ce résultat nous donne une compacité d’environ 0,52 soit 52 %. Comme je vous le disais, l’empilement cubique simple n’est pas très compact. Presque la moitié du volume de la maille est inoccupé.
Compacité de la maille CFC
Calculer la compacité de la maille CFC.
Correction

La diagonale d’une face $*d*$ vaut 4 fois le rayon $*r*$. D’autre part, la diagonale d’un carré de côté $*a*$ vaut $*a\sqrt{2}*$. Donc on a : $*a\sqrt{2}=4r*$.
Dans une maille CFC, il y a 4 atomes, comme on l’a vu plus haut.
Calcul de la compacité $*c*$ :
$µ \begin{aligned}
c &= \frac{4×V_{\mathrm{atome}}}{V_{\mathrm{maille}}} \\
c &= \frac{4×\frac 43 \pi r^3}{ \left( \frac{4r}{\sqrt{2}} \right)^3} \\
c &= \frac{\frac {16}3 \pi}{ \frac{64}{2\sqrt{2}}} \\
c &= \frac{32 \sqrt{2} \pi}{192} \\
c &\simeq 0,74
\end{aligned}
µ$
La compacité de la structure CFC est d’environ 74 %
Masse volumique d’un cristal
On peut prévoir la masse volumique d’un cristal si on connaît la masse molaire des atomes qui le constitue et son paramètre de maille.
Le polonium, par exemple, a une masse molaire de 209 g·mol-1. Son paramètre de maille vaut $*a*$ = 0,340 nm. Il cristallise dans une structure cubique simple. Comment déduire la masse volumique du polonium solide de ces données ? Eh bien juste avec un peu de géométrie… 😊
Le volume d’une maille vaut $*V*$ = $*a^3*$ = 3,93·10-29 m3 (il est préférable de le calculer en m3).
Combien pèse une maille ? Pour ça il faut se rappeler ce qu’on a dit plus haut, à savoir qu’il y a 8×⅛ = 1 atome par maille (c’est une structure cubique simple). Du coup, une maille pèse la même chose qu’un atome de polonium.
Combien pèse un atome de polonium ? Eh bien on sait qu’une mole de $*\ce{Po}*$ pèse 209 g et qu’il y a 6,02·1023 atomes pour chaque mole.
Il est préférable de convertir cette masse molaire en kg·mol-1 : 209 g·mol-1 = 0,209 kg·mol-1.
Donc un atome de $*\ce{Po}*$ pèse 209·10-3÷6,02·1023 = 3,47·10-25 kg.
Dernière étape : il n’y a plus qu’à calculer la masse volumique d’une maille (qui est la même que celle du cristal dans son ensemble, puisque le cristal est constitué d’un très grand nombre de mailles).
$µ \rho = \frac mV = \frac{3,47·10^{-25}}{3,93·10^{-29}} µ$
On trouve $*\rho*$ = 8,8·103 kg·m-3. Et voilà. On a trouvé la masse volumique du polonium.
La valeur expérimentale est de 9,2·103 kg·m-3. On voit que la valeur calculée n’est pas loin de la valeur expérimentale.
Le cristal de fer
Le fer peut cristalliser en différentes structures cristallines dites allotropiques. L’une d’entre elle est la structure CFC que vous connaissez bien. Son paramètre de maille vaut $*a*$ = 0,356 nm.
1. Représentez la structure CFC en perspective cavalière (en 3D) et déduisez-en le rayon atomique du fer dans ce cas.
2. Calculez la masse volumique du fer dans cette structure, en kg·m-3. La masse molaire du fer vaut 55,8 g·mol-1.
Correction
1. Voir le schéma correspondant à la maille CFC un peu plus haut dans le cours.
On en déduit que le rayon atomique du fer vaut 4 fois la diagonale de la face de la maille CFC (voir également l’exercice Compacité de la maille CFC).
Soit $*r = \frac {a\sqrt{2}}4 =*$ 0,126 nm
2. On calcule le volume d’une maille : $*V = a^3 =*$ 4,51·10-29 m3.
On calcule ensuite la masse d’une maille : chaque maille contient 4 atomes (voir la justification plus haut dans le cours).
D’autre part, la masse d’un atome de fer vaut $*\dfrac{M_\text{Fe}}{N_A} =*$ 9,27·10-26 kg.
Donc chaque maille pèse $*m*$ = 4×9,27·10-26 = 3,71·10-25 kg.
La masse volumique du fer dans ce système cristallin vaut :
$µ \rho = \frac mV = 8,2·10^3 \; \text{kg·m}^{-3} µ$
Les cristaux dans la Nature
- Distinguer, en termes d’échelle et d’organisation spatiale, maille, cristal, minéral, roche.
- Les identifier sur un échantillon ou une image.
Beaucoup de solides ont une structure cristalline. Dans la Nature, il y a bien sûr l’eau, ou plus exactement la glace 😊, les roches, qui sont composées de minéraux sous forme de cristaux, mais on en trouve aussi dans les êtres vivants (les os, l’émail dentaire, les coquilles de mollusques…).
Formes allotropiques
Une même espèce chimique peut cristalliser sous différentes formes. Par exemple, le fer peut cristalliser sous 3 différentes formes (on dit qu’il a 3 formes allotropiques différentes) : α (cubique centré), γ (cubique à faces centrées) et ε (hexagonale compacte). Ça dépend de la pression et de la température à laquelle il est soumis.
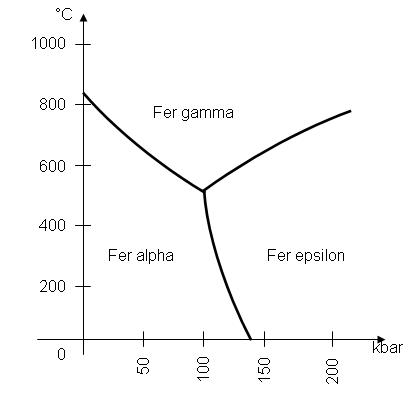
Certaines propriétés macroscopiques d’une même espace chimique (comme la densité, par exemple) peuvent dépendre de la structure cristalline dans laquelle elle se trouve. L’exemple le plus flagrant est celui du carbone. Une des formes allotropiques du carbone, c’est le graphite (votre mine de crayon). L’autre, c’est le diamant…

Roches, minéraux et cristaux
Les roches sont formées, essentiellement ou en totalité, par un assemblage de minéraux, comportant parfois des fossiles, du verre résultant du refroidissement rapide du magma (on y reviendra plus loin) ou des agrégats d’autres roches. Les roches peuvent être formées d’une seule espèce minérale ou de plusieurs.
Un minéral est un solide naturel homogène constitué de matière cristallisée caractérisée par sa composition chimique et sa structure.
Le granite, par exemple, est une roche très courante composée de plusieurs types de minéraux : du quartz (Q) de formule $*\ce{SiO2}*$, du feldspath orthose (FelO) $*\ce{KAlSi3O8}*$, du feldspath plagioclase (FelP) $*\ce{NaAlSi3O8}*$ ou $*\ce{CaAl2Si2O8}*$ et de la biotite (B) $*\ce{K(Fe,Mg)3[Si3AlO10 (OH,F)2]}*$.


Retenez que certaines roches sont composées de cristaux plus ou moins gros d’un ou plusieurs types de minéraux.
Les solides amorphes
Je vous ai dit que la plupart des solides étaient des cristaux. La plupart, oui… mais pas tous. Ne parlons pas de solides composés de très grosses molécules organiques diverses, comme le fromage, la viande, etc. C’est hors sujet ici. Mais parlons d’un solide très dur que vous connaissez bien, le verre.
Le verre, c’est de la silice, $*\ce{SiO2}*$, comme le quartz dont on a parlé tout à l’heure. Mais à la différence du quartz, la silice qui le compose, lorsqu’elle était à l’état liquide, s’est refroidie très rapidement. Les molécules n’ont pas eu le temps de s’ordonner en un cristal. Elles ont gardé la même organisation qu’à l’état liquide (c’est-à-dire qu’elles sont désordonnées), mais elles se sont figées dans cet état.
On dit que le verre est un solide amorphe.
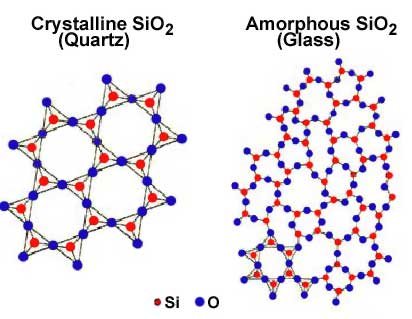
Le verre existe à l’état naturel dans certaines roches volcaniques dont le refroidissement a été rapide.
De manière générale, plus le refroidissement d’un liquide est lent, meilleure sera la cristallisation à l’état solide. Si vous voulez obtenir de beaux cristaux de sel, faites évaporer de l’eau salée à l’air libre, plutôt qu’en la chauffant.
Roches magmatiques de la croûte océanique
D’après un exercice du Livre Scolaire
Le fond des océans est le siège d’une activité volcanique principalement localisée au niveau des dorsales. Les roches formées sont alors essentiellement des gabbros et des basaltes, et constituent la croûte océanique.

Que peut-on conclure après examen de la structure de ces deux roches ?
Correction
Dans le gabbro, les cristaux de minéraux sont beaucoup plus gros que dans le basalte. Donc ils ont refroidi plus lentement que ces derniers.
Révision & entraînement
Carboglace
D’après un exercice du Livre Scolaire
La carboglace est la forme solide du dioxyde de carbone $*\ce{CO2}*$. Elle cristallise sous la forme d’un réseau cubique à faces centrées.
Densité de la carboglace : 1,56
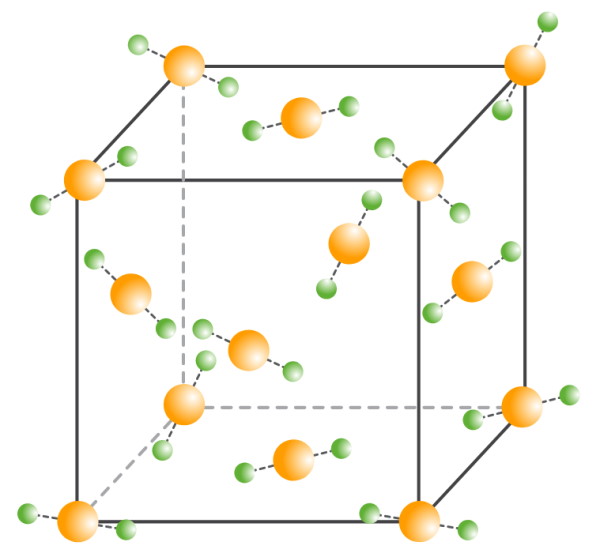
1. Calculer la masse d’une molécule de $*\ce{CO2}*$ en cherchant les données dont vous avez besoin (tout est sur mon site 😊 ).
2.a. En utilisant la densité de la carboglace, déterminer le paramètre $*\alpha*$ de la maille…
2.b. … puis la distance entre deux atomes de carbone de deux molécules de $*\ce{CO2}*$ voisines , c’est-à-dire entre un atome de carbone se trouvant à l’un des sommets de la maille, et un autre se trouvant au milieu d’une face associée à ce sommet.
Correction
1. $*m = \frac{M_\ce{CO2}}{N_A} = \frac{0,044}{6,02·10^{23}} =*$ 7,31·10-26 kg. (on exprime la masse molaire en kg·mol-1 pour avoir la masse d’une molécule en kg (mais on peut aussi faire la conversion après le calcul de la masse d’une molécule).
2.a. La densité de la carboglace vaut 1,56, donc sa masse volumique vaut $*\rho*$ = 1,56·103 kg·m-3.
Comme il s’agit d’une structure CFC, il y a 4 molécules de $*\ce{CO2}*$ par maille, donc la masse d’une maille vaut 2,92·10-25 kg.
Donc le volume d’une maille vaut :
$µ V = \frac m{\rho} = \frac {2,92·10^{-25}}{1,56·10^3} = 1,87·10^{-28} \; \text{m}^3 µ$
Et donc, le paramètre de maille vaut $*\alpha = \sqrt[3]{V} = *$ 5,72·10-10 m.
2.b. Deux atomes de carbone voisins sont distants de la moitié de la diagonale d’une face de la maille, soit $*\alpha \frac{\sqrt{2}}2*$ = 4,05·10-10 m (ou 0,405 nm).
Cristal de polonium
Cet exercice est tiré d’une épreuve d’E3C
Données
- Le polonium cristallise dans le réseau cubique simple.
- Paramètre de maille : $*a*$ = 3,36·10-10 m
- Masse molaire du polonium $*M(\ce{Po})*$ = 210 g∙mol-1
- Nombre d’Avogadro $*N_A*$ = 6,02·1023 mol-1
- Une poussière ou un grain de matière d’un volume inférieur à 10-11 m3 est invisible à l’œil nu.
1. Représenter la structure cubique simple du polonium en perspective cavalière.
2. Dénombrer, en indiquant les calculs effectués, le nombre d’atomes par maille.
3. Calculer la compacité de l’empilement cubique simple, en considérant que les atomes sont en contact les uns avec les autres et qu’ils se comportent comme des sphères indéformables.
4. Montrer que la masse volumique du polonium est de 9,20·106 g·m-3.
5. Montrer qu’un morceau de polonium d’une masse de 10 µg est invisible à l’œil nu.
Correction
1. Schéma structure cubique simple

2. Pour une maille, il y 1 atome sur chacun des 8 sommets. Chaque atome est partagé par 8 mailles. Nombre d’atomes par maille : 8×⅛ = 1
3. Volume d’une maille : $* V_m = a^3 = *$ (3,36·10-10)3 = 3,79·10-29 m3
Rayon d’un atome : dans une maille cubique simple, deux atomes sur deux sommets voisins sont adjacents. Donc l’arête d’une maille est égale à deux fois le rayon de l’atome.
Volume d’un atome : $* V_a = \dfrac 43 \pi ×(\dfrac a2)^3*$ = 1,99·10-29 m3.
Compacité : volume occupé par les atomes ÷ volume d’une maille = 1,99÷3,79 = 0,52.
On peut faire le calcul de manière plus directe : $* \dfrac {\frac 43 \pi ×( \frac a2)^3} {a^3} = \dfrac π6 *$
4. Masse volumique = masse d’une maille ÷ volume d’une maille.
Or on a un seul atome par maille, donc la masse d’une maille est égale à la masse d’un atome.
Masse d’un atome : 210÷6,02·1023 = 3,488·10-22 g. (voir exercice sur le polonium du chapitre précédent).
Donc $* \rho = \dfrac {3,488·10^{-22}}{3,79·10^{-29}} = 9,20·10^6 *$ g·m3
5. Volume d’une masse de 10 µg de polonium : $*V = \dfrac m\rho = \dfrac {10^{-6}}{9,2·10^6} = 1,1·10^{-13}*$ m3.
Ce volume est très inférieur à 10-11 m3 donc invisible à l’œil nu.