2.1 Le rayonnement solaire
Le Soleil et la fusion nucléaire
- Déterminer la masse solaire transformée chaque seconde en énergie à partir de la donnée de la puissance rayonnée par le Soleil.
La fusion nucléaire au cœur du Soleil
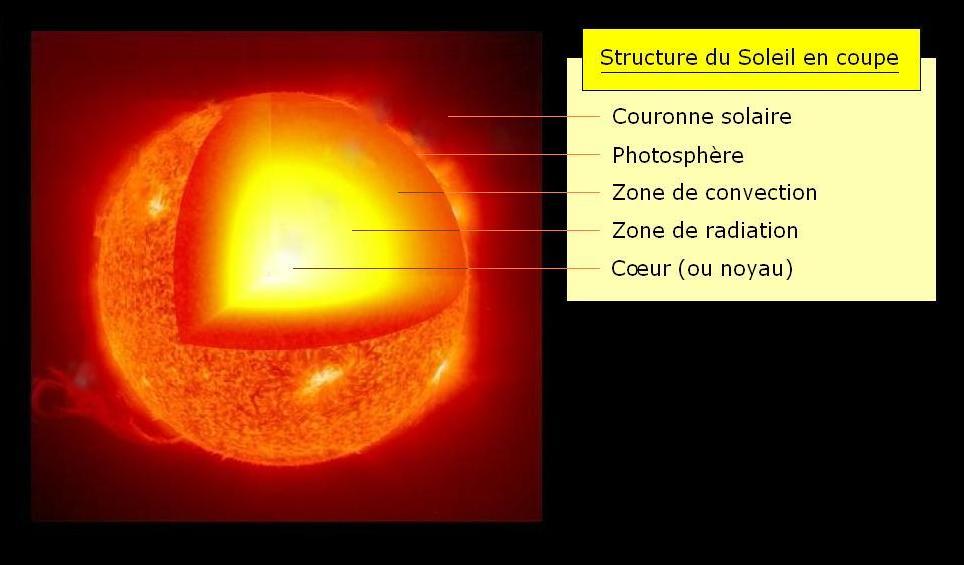
Le Soleil est, comme toutes les étoiles, une gigantesque boule de gaz (essentiellement de l’hydrogène) extrêmement chaude.
Deux forces s’opposent dans le Soleil et contribuent à sa stabilité :
- L’attraction gravitationnelle dont l’effet est de contracter sur elle-même la matière qui constitue le Soleil. Le Soleil étant formé d’une grande quantité de matière (sa masse est environ 300.000 fois plus élevée que celle de la Terre), celle-ci a tendance à s’effondrer sur elle-même sous l’effet de sa propre gravité.
- La pression interne, due à l’énorme dégagement d’énergie engendré par les réactions de fusion nucléaire qui se déroulent dans le cœur du Soleil, repousse cette matière vers l’extérieur de l’étoile.
Au cœur du Soleil, où règne une température d’environ 15 millions de °C, les atomes d’hydrogène fusionnent entre eux, libérant ainsi une très grande quantité d’énergie sous forme de chaleur et de radiations.
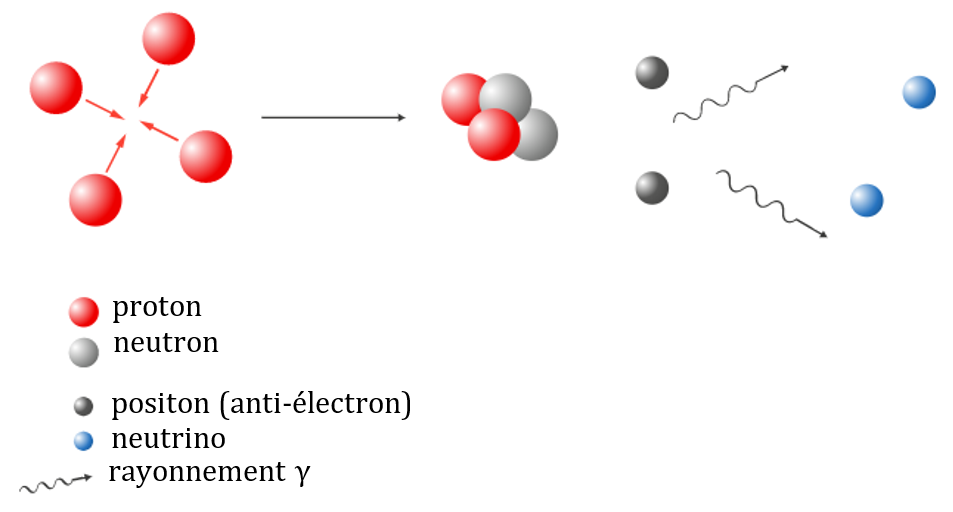
Équation-bilan de la fusion nucléaire se déroulant dans le Soleil
$µ \ce{ 4 ^1_1H \rightarrow \ ^4_2He + 2 e^+ + 2 \nu \+ 2 \gamma } µ$
Principe d’équivalence masse-énergie
Einstein a découvert que la matière n’est rien d’autre qu’une forme d’énergie très condensée. C’est la fameuse formule $*E = mc^2*$.
L’énergie produite par le Soleil correspond en fait à une infime partie de sa masse se transformant en énergie, au cours de la fusion nucléaire. Donc cette production d’énergie s’accompagne d’une perte de masse du Soleil. Le lien entre le dégagement d’énergie $*E*$ et la perte de masse $* \Delta m*$ se calculer en utilisant la formule :
| $*E = \Delta m · c^2 *$ |
$*E*$ : énergie dégagée (J) $*\Delta m*$ : perte de masse (kg) $*c*$ : vitesse de la lumière (3,00·108 m·s-1) |
Énergie & puissance
Une puissance est un débit d’énergie : c’est la quantité d’énergie dégagée ou absorbée par un système chaque seconde. $µ P = \frac E{\Delta t} µ$ Une puissance s’exprime en watt (W) : 1 W = 1 J·s-1.Équivalence masse-énergie
Le soleil rayonne une puissance de 3,85·1026 W.
1. En 2017, l’humanité a consommé environ 4·1020 J. Combien de temps faut-il au Soleil pour rayonner cette énergie ?
2. Calculer la masse que le Soleil transforme en énergie chaque seconde. Comparer cette masse à la masse de la pyramide de Khéops (5 millions de tonnes).
3. La combustion d’un litre d’essence dégage environ 30 MJ. Quelle est la masse perdue lors de la réaction ? Comparer cette masse à celle d’une (petite) fourmi soit 1 mg.
Correction
1. On utilise la relation $*P = \frac E{\Delta t}*$.
$* \Delta t = \frac EP = *$ 4·1020/3,85·1026 ≃ 10-6 s
Il faut 1 µs au Soleil pour rayonner toute l’énergie que l’humanité utilise en un an.
2. En une seconde, le Soleil perd 3,85·1026 J.
$*\Delta m = \frac E{c^2} =*$ 3,85·1026/(3·108)2 = 4,28·109 kg
La pyramide de Khéops a une masse de 5·106×103 = 5·109 kg.
La masse perdue par le Soleil chaque seconde est voisine de celle de la pyramide de Khéops.
3. $*\Delta m = \frac E{c^2} =*$ 30·106/(3·108)2 ≃ 3,3·10-10 kg soit 0,00033 mg.
C’est environ 3.000 fois plus petit que la masse d’une petite fourmi.
Rayonnements émis par le Soleil
- À partir d’une représentation graphique du spectre d’émission du corps noir à une température donnée, déterminer la longueur d’onde d’émission maximale.
- Appliquer la loi de Wien pour déterminer la température de surface d’une étoile à partir de la longueur d’onde d’émission maximale.
Rayonnement thermique
Tous les corps matériels émettent un rayonnement électromagnétique dont les caractéristiques dépendent de leur température. Ce faisant, ils perdent de l’énergie par rayonnement.
Des corps très froids (par exemple des nuages de gaz et de poussière interstellaires qui ont une température d’environ 10 kelvins, soit –263 °C) émettent un rayonnement électromagnétique situé dans le domaine des micro-ondes.
Les corps plus chauds émettent des rayonnements de longueurs d’onde plus courtes. S’ils sont assez chauds, ils peuvent émettre des rayonnements visibles (un morceau de fer chauffée au rouge, par exemple).

Spectre d’émission d’un corps noir
Un « corps noir », en physique est un corps « idéal » qui absorberait tout le rayonnement qu’il reçoit. Un tel corps émet un rayonnement qui ne dépend que de sa température (loi de Planck).
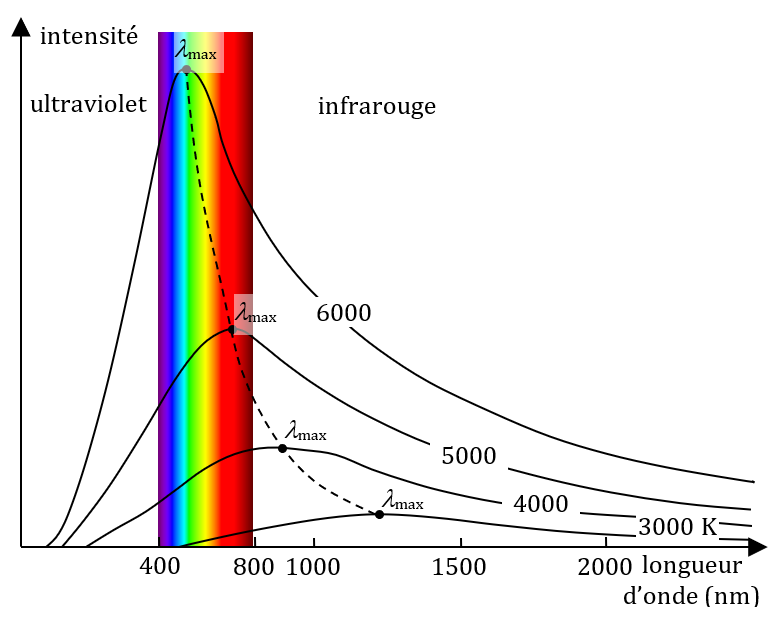

Les étoiles, dont le Soleil, se comportent de manière assez similaire à un corps noir. Il est donc possible de déduire leur température de surface à partir de leur spectre.

Ce spectre du Soleil nous permet d’estimer sa température de surface : environ 6000 K.
Loi de Wien
La loi de Wien permet de connaître la longueur d’onde du maximum d’émission $*\lambda_{\max}*$ selon la température, pour un corps noir.
| $µ \lambda_{\max} = \frac {2,90·10^{-3} \, \mathrm{m·K}}T µ$ | $*\lambda_{\max}*$ : longueur d’onde du maximum d’émission, en mètre $*T*$ : température en kelvin (K) |
Sur l’échelle de Kelvin, 0 K = -273 °C (il s’agit du zéro absolu). Une augmentation de 1 K correspond à une augmentation de 1 °C. $µ T(\text{K}) = \theta (\text{°C}) + 273 µ$
Exemple : pour une étoile dont la température de surface est de 5800 K, $*\lambda_{\max}*$ = 2,9·10-3 / 5800 = 5,0·10-7 m. Cela signifie que la longueur de la radiation qui est le plus produite par l’étoile est de 500 nm.
Loi de Wien
1. Rigel est une étoile bleutée de la constellation d’Orion. La longueur d’onde correspondant au maximum de son émission est dans le domaine ultraviolet et vaut $*\lambda_{\max}*$ = 210 nm. Donner une estimation de la température de surface de cette étoile en degré Celsius.
2. Un souffleur de verre sort la pâte de silice fondue du four à la température de 1550 °C.

Calculer la longueur d’onde dans le vide $*\lambda_{\max}*$ du maximum d’intensité du rayonnement de la pâte de silice à cette température. Dans quel domaine se trouve $*\lambda_{\max}*$ ? Pourquoi une partie du rayonnement émis est-il visible ?
Correction
1. $* T = \cfrac{2,90·10^{-3}}{210·10^{-9}}*$ ≃ 13,8·103 K soit environ 13500 °C.
2. $*\lambda_{\max}*$ ≃ 1,6 µm. Ceci correspond aux IR. Cependant de la lumière visible est quand-même émise, car $*\lambda_{\max}*$ correspond à la longueur d’onde du maximum d’émission, mais ça ne signifie pas que c’est la seule longueur d’onde émise.
Une lumière « chaude »
Traversé par un courant électrique, le filament en tungstène d’une ampoule est porté à 2 700 K. Voici le spectre de la lumière visible émise.
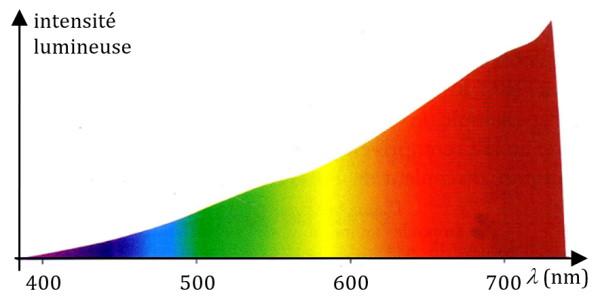
1. Calculer $*\lambda_{\max}*$. Dans quel domaine du spectre électromagnétique se trouve cette longueur d’onde ? Est-ce cohérent avec le spectre ci-dessus ?
2. Quelle est la couleur de la lumière solaire ? Expliquer pourquoi la lumière d’une ampoule à filament apparaît plus rouge que celle du Soleil.
3. On dit que la lampe à incandescence présente une lumière « plus chaude » que la lumière du jour. Est-ce cohérent avec la température des deux sources lumineuses ?
Correction
1. $*\lambda_{\max}*$ = 1,1 µm. Cela correspond au IR. C’est cohérent avec le spectre montré, car on voit que son maximum se situe au-delà du rouge.
2. La lumière solaire est blanche. Par contre, la lumière du filament est beaucoup plus riche en rouge qu’en bleu, d’où une couleur rougeâtre de cette lumière.
3. Non, une couleur est dite « chaude » dans le langage courant si sa teinte est jaune, orange ou rouge. Mais elle est produite par une source plus froide (le filament) qu’une source de lumière blanche (le soleil).
Climats & saisons
- Sur un schéma, identifier les configurations pour lesquelles la puissance reçue par une surface est maximale ou minimale.
- Analyser, interpréter et représenter graphiquement des données de températures. Calculer des moyennes temporelles de températures. Comparer des distributions temporelles de températures
La puissance radiative reçue du Soleil par une surface plane dépend de l’angle entre la normale à la surface et la direction du Soleil.
Imaginons un faisceau de rayons solaires délimités par le cercle en pointillés ci-dessous.
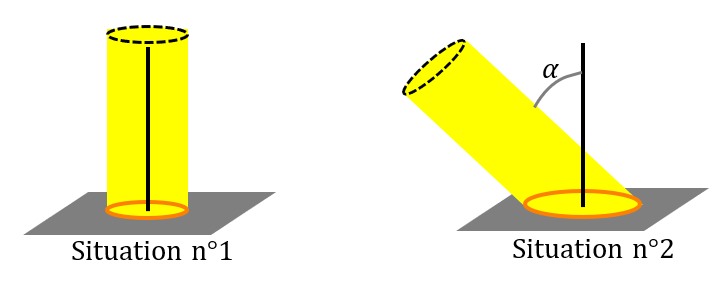
Dans la situation n°1, $*\alpha*$ = 0. Les rayons du soleil sont perpendiculaires à la surface éclairée. La puissance radiative reçue par unité de surface éclairée est maximale.
Dans la situation n°2, le faisceau de rayons du soleil a la même largeur que dans la situation n°1 (c’est-à-dire que la surface du cercle en pointillés est la même), mais le fait que $*\alpha \neq *$ 0 implique que la puissance radiative est répartie sur une plus grande surface (la surface délimitée en orange dans la situation n°2 est plus grande que celle dans la situation n°1, et pourtant, c’est deux surfaces reçoivent la même puissance lumineuse car elles sont éclairées par un faisceau de même diamiètre). Donc la puissance radiative reçue par unité de surface est plus faible si $*\alpha \neq *$ 0.
Ceci explique les variations de l’énergie solaire reçue par unité de surface en fonction de l’heure, de la saison et de la latitude. Nous allons voir ceci en détails dans les paragraphes suivants.
Variations saisonnières
L’axe de rotation de la Terre est incliné d’un angle d’environ 23° par rapport au plan de l’écliptique (plan dans lequel la Terre orbite autour du Soleil, en bleu sur le schéma ci-dessous). Ceci explique les variations saisonnières de température.
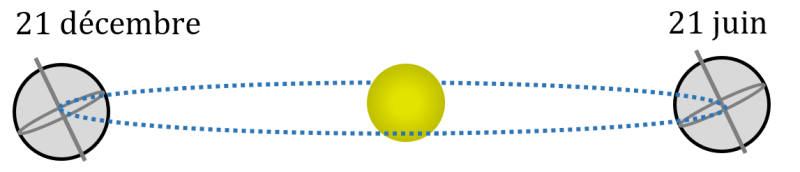
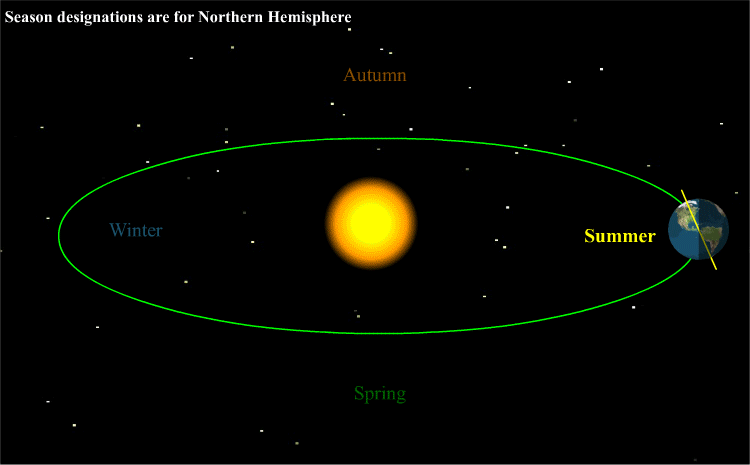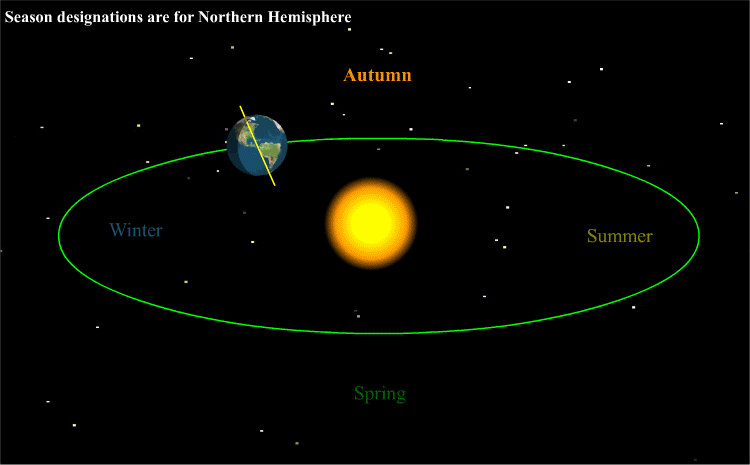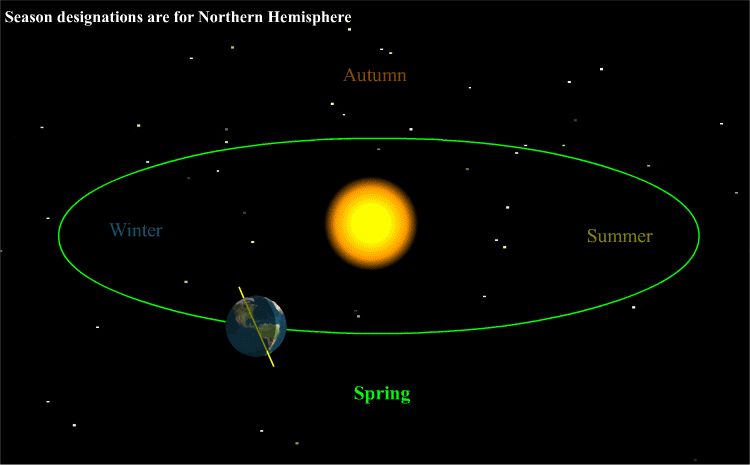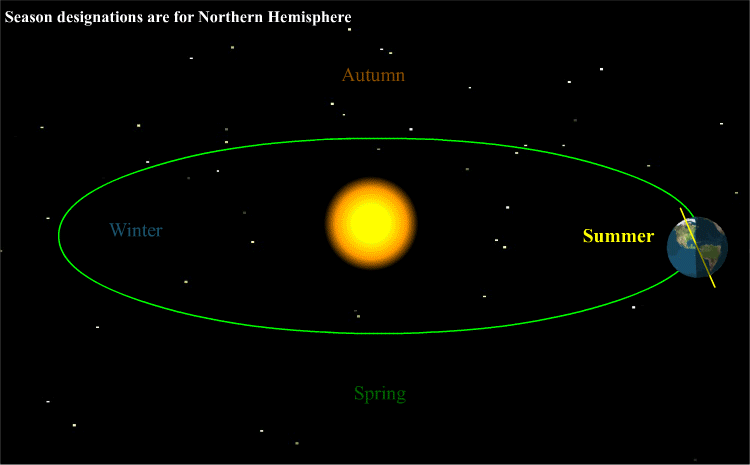
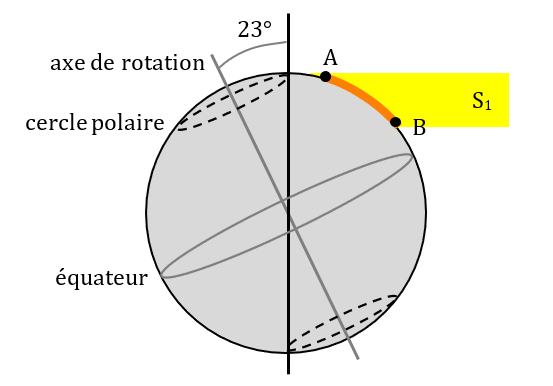
Le schéma ci-dessus montre la Terre le 21 décembre. C’est l’hiver dans l’hémisphère Nord et l’été dans l’hémisphère Sud. Un faisceau de rayons du Soleil de section S1 éclaire une surface délimitée en orange entre les points A et B dans l’hémisphère Nord.
6 mois plus tard, vous voyez qu’un faisceau de même section S1 éclaire une surface beaucoup plus petit que le 21 décembre. Une même puissance radiative est concentrée sur une surface au sol plus petite. Il fait donc plus chaud.
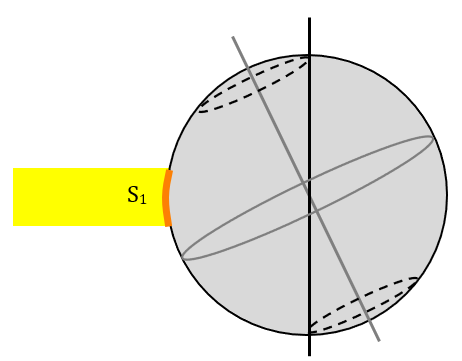
Latitudes et climat
On voit également sur le schéma ci-dessus que plus la latitude est élevée (c’est-à-dire, plus on se rapproche des pôles), plus les rayons solaires arrivent inclinés par rapport au sol. Au niveau du point A, les rayons solaires arrivent très inclinés. Au niveau du point B, c’est toujours l’hiver, mais les rayons arrivent moins inclinés qu’en A. Il fera donc moins froid en B qu’en A.
Ceci explique que le climat est plus froid aux latitudes élevées (zone tempérée, zone arctique) qu’aux faibles latitudes (zones tropicales).
Variations journalières
La puissance radiative reçue par unité de surface pour un endroit donné et une saison donnée dépend également de l’heure solaire. Le matin et le soir, les rayons solaires arrivent plus inclinés à la surface de la Terre qu’en milieu de journée.
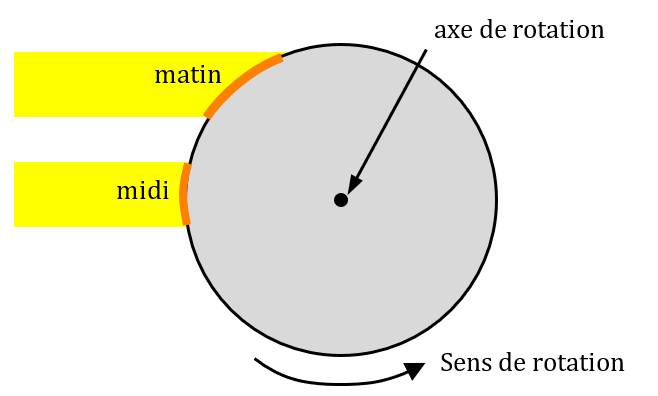
Inclinaison des rayons du Soleil
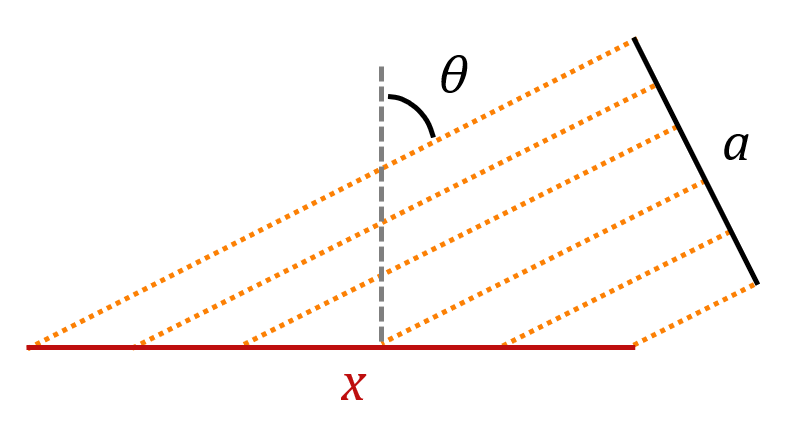
Le but de cet exercice est de vous faire comprendre le lien mathématique entre l’inclinaison des rayons du Soleil et la puissance radiative reçue par le sol.
1. Exprimer la longueur $*x*$ en fonction de la longueur $*a*$ et de l’angle $*\theta*$. Les rayons du Soleil (en pointillés orange), sont perpendiculaires au segment $*a*$ et le segment gris en pointillé au perpendiculaire au sol.
La puissance solaire maximale à la surface de la Terre est d’environ 1000 W·m-2 lorsque les rayons arrivent perpendiculairement au sol.
En hiver, en Serbie, l’angle d’incidence le plus faible, c’est-à-dire celui qui correspond au soleil le plus haut dans le ciel (à midi), est de l’ordre de 80°.
2.a. En faisant le rapprochement entre les situations présentées ci-dessus et la figure de la question 1, que vaut $*\theta*$ lorsque la puissance solaire vaut 1000 W·m-2 ?
2.b. Quelle est la puissance solaire maximale reçue au niveau du sol en hiver en Serbie ?
Correction
1. Pour répondre à cette question, il suffit de remarquer ce que j’ai rajouté en vert sur la figure.
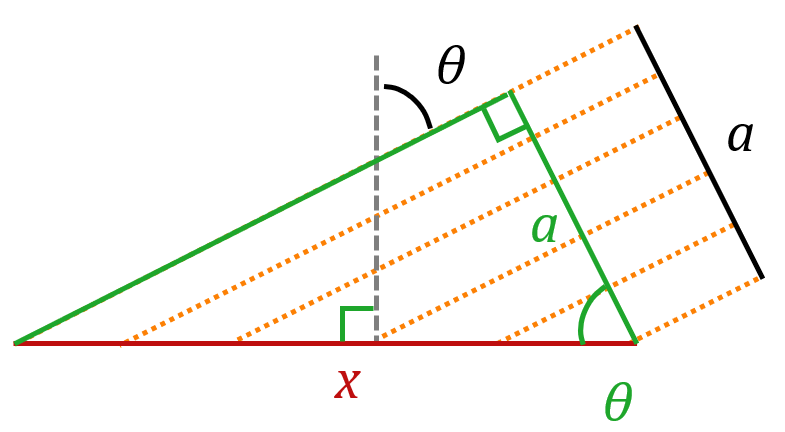
Ce qui permet de voir que $*\cos \theta = \cfrac ax *$.
On a donc $*x = \cfrac a{\cos \theta}*$
2.a. Quand le soleil éclaire perpendiculairement le sol, $*\theta*$ = 0.
2.b. On réutilise le résultat de la question 1. Lorsque $*\theta*$ = 80°, $*x*$ est $* \frac 1{\cos 80}*$ = 5,8 fois plus grand que $*a*$. Donc la puissance reçue est répartie sur une surface 5,8 plus grande que la surface éclairée lorsque l’angle d’incidence vaut 0. Donc chaque metre carré reçoit une puissance 5,8 fois plus petite, c’est-à-dire environ 174 W.
Changement climatique
Imaginons que subitement, l’inclinaison de l’axe de rotation de la Terre passe de 23,5 ° à 0° et que sa rotation devienne beaucoup plus lente, passant de 24 h à une semaine.Quels effets cela aurait-il sur les variations de températures journalières et annuelles ?
Correction
Si l’obliquité (c’est-à-dire l’inclinaison de l’axe de rotation) de la Terre est nulle, il n’y a plus de saisons. Le climat est le même toute l’année.
Avoir une rotation plus lente implique que les températures montent plus lentement le « matin », mais elles montent beaucoup plus longtemps, donc beaucoup plus haut (le « midi » est atteint au bout d’un quart de semaine, soit 42 h).
La nuit, la température baisse pendant beaucoup plus longtemps également. Ce qui fait que l’amplitude des variations de température au cours d’une « journée » de 168 h sera très importante.
Révision & entraînement
Énergie rayonnée par l’étoile Véga
1. Nommer et décrire le mécanisme qui est à l’origine de l’énergie rayonnée par une étoile.
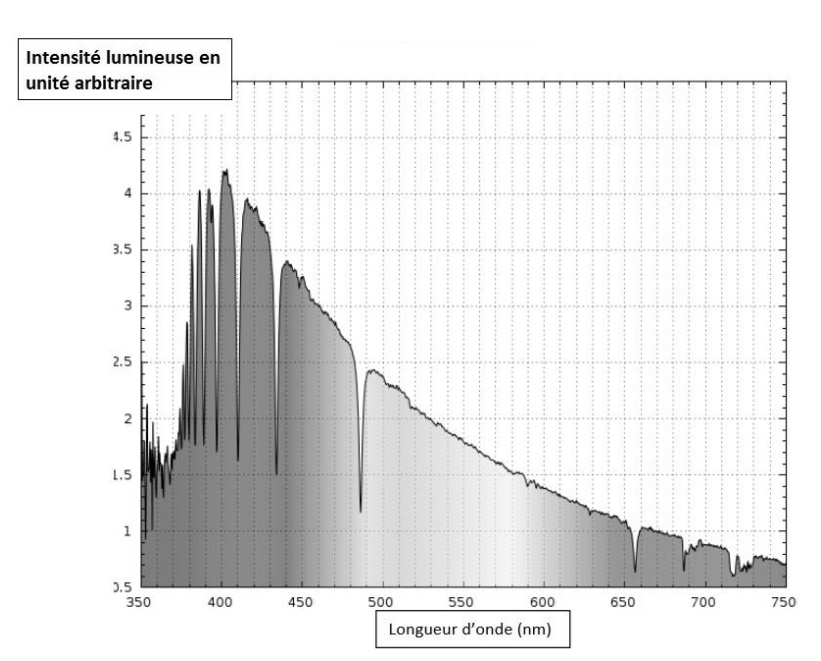
La longueur d’onde correspondante à l’intensité lumineuse maximale pour le Soleil est $* \lambda_\max *$ = 500 nm.
2. La température de surface de Véga est-elle supérieure ou inférieure à celle du Soleil. Justifier.
3. Quelle est la température de surface de Véga en °C ?
Correction
1. Il s’agit de la fusion nucléaire. Au cours de ce processus, des noyaux atomiques légers fusionnent pour former des noyaux plus lourds.
2. Le $*\lambda_\max*$ de Véga est voisin de 410 nm. C’est plus petit que le $* \lambda_\max *$ du Soleil. Donc Véga est plus chaude que le Soleil.
3. On utilise la loi de Wien. Température de surface de Véga : $µ T = \frac{2,90·10^{-3}}{\lambda_\max} = \frac{2,90·10^-3}{410·10^{-9}} µ$ $*T*$ ≃ 7000 K, soit environ 6700 °C