3.1 La forme de la Terre
La Terre est ronde ! Comment l’a-t-on découvert ? Comment se repérer sur la Terre ?
Sphéricité de la Terre
- Calculer la longueur du méridien terrestre par la méthode d’Ératosthène.
- Calculer une longueur par la méthode de triangulation utilisée par Delambre et Méchain.
- Calculer le rayon de la Terre à partir de la longueur du méridien.
Apparition de l’idée de sphéricité
L’idée d’une Terre sphérique est apparue vers 500 av. J.-C. Elle est attribuée à Pythagore. Elle est définitivement admise par les lettrés grecs vers 300 av. J.-C. grâce aux arguments proposés par Aristote :
- Lors d’une éclipse de Lune, l’ombre de la Terre sur la Lune a une forme circulaire.
- L’aspect du ciel change lorsqu’on se déplace vers le Nord et vers le Sud : certaines étoiles apparaissent et d’autres disparaissent.
- Il pense que la Terre s’est formée par agglomération de ces composants sous l’effet « d’une tendance naturelle des objets à se diriger vers un point central ». Donc, pour des raisons de symétrie et d’équilibre, elle ne peut être que sphérique.

Mesure du rayon de la Terre par Ératosthène
Ératosthène de Cyrène (273–192 av. J.-C.) découvre que l’angle que font les rayons du Soleil avec la surface du sol, lorsque celui-ci est à son zénith (position la plus haute dans le ciel), pour une date donnée, dépend de la latitude de l’endroit où l’on se trouve.
Comme il savait que le Soleil est très éloigné de la Terre (et donc que ses rayons arrivent sur Terre parallèle entre eux) il en conclut que la Terre est forcément ronde, et est capable de calculer son diamètre.
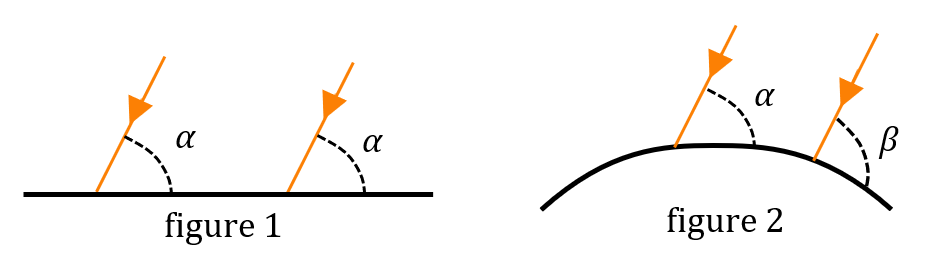
Figure 1 : hypothèse de la Terre plate. Les rayons forment tous un même angle $*\alpha*$ avec le sol.
Figure 2 : hypothèse de la Terre sphérique. L’angle que forme les rayons du Soleil avec le sol dépend de la latitude.
La méthode d’Ératosthène
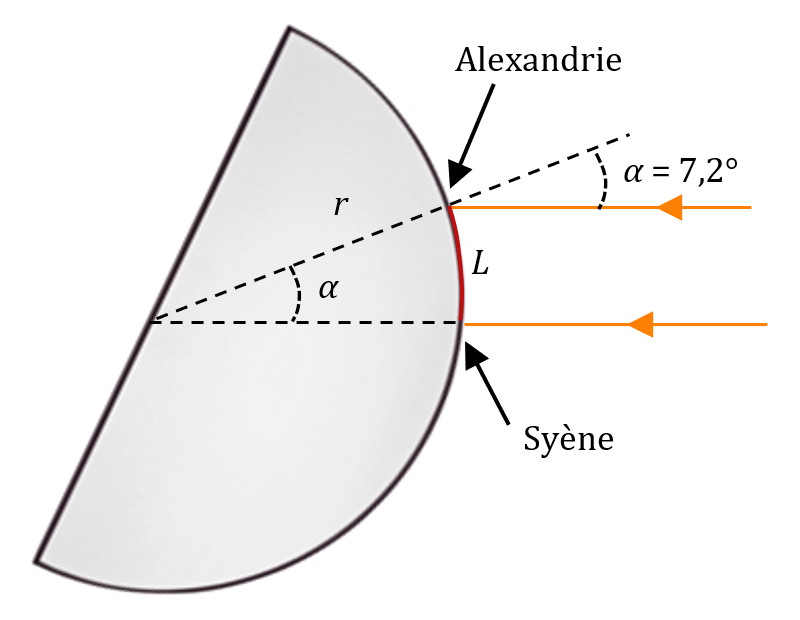
Ératosthène disposait des données suivantes, trouvées dans la bibliothèque d’Alexandrie ou déduites de ses observations et de mesures :
• Dans les mêmes conditions à Alexandrie, les rayons du soleil forment un angle de 7,2° avec la verticale.
• Alexandrie est à 800 km parfaitement au nord de Syène.
Voici la situation schématisée :
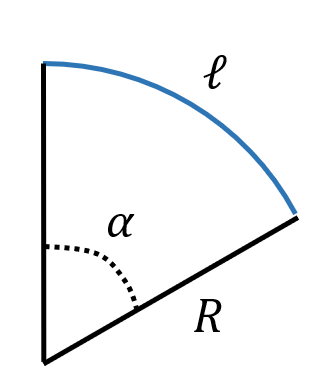
Longueur d’un arc de cercle
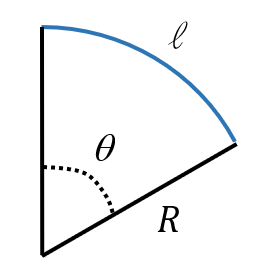
$* \ell = \theta R*$ si $* \theta *$ est exprimé en radian
Ératosthène connaissait donc la longueur de l’arc de cercle séparant Alexandrie de Syène et l’angle entre les deux rayons qui passent par ces villes.
• $*L*$ = 800 km
• $*\alpha*$ = 7,2° ≃ 0,126 radian
Il a donc pu déterminer le rayon de la Terre avec une bonne précision, en utilisant la formule $*L = \alpha ·r*$ :
$*r = L/ \alpha *$ = 800 / 0,126 ≃ 6370 km
Remarque : en fait, les valeurs dont disposait Ératosthène n’étaient pas aussi précises que celle qu’on a utilisées ici. Il est arrivé à un rayon de la Terre de 6260 km au lieu de 6370. Ce qui fait tout de même moins de 2 % d’erreur !
Méthode d’Ératosthène, cas général
Que faire si aucun point de référence ne se trouvent sur le tropique ? C’est-à-dire si le Soleil n’est jamais à la verticale d’aucun des points ? Eh bien on peut quand-même y arriver ! 😊
Le 21 juin, au midi solaire, à Belgrade, les rayons du Soleil forment un angle $*\alpha*$ = 21,3° avec la verticale.
Au même moment de l’année, à Corfou, située 580 km au Sud, les rayons de Soleil forment un angle $*\beta*$ = 16,1° avec la verticale.
On rappelle que Corfou ne se situe pas en zone tropicale… 🙄 Et donc que les rayons arrivant à Corfou à ce moment sont inclinés vers le sud.
1. Faire un schéma de la situation faisant figurer la Terre, les deux villes, la distance de 580 km et les deux angles $*\alpha*$ et $*\beta*$.
2. Exprimer l’angle formé par le rayon passant par Belgrade et celui passant par Corfou en fonction de $*\alpha*$ et $*\beta*$.
3. Retrouver la valeur du rayon de la Terre (environ 6380 km) grâce à ces données.
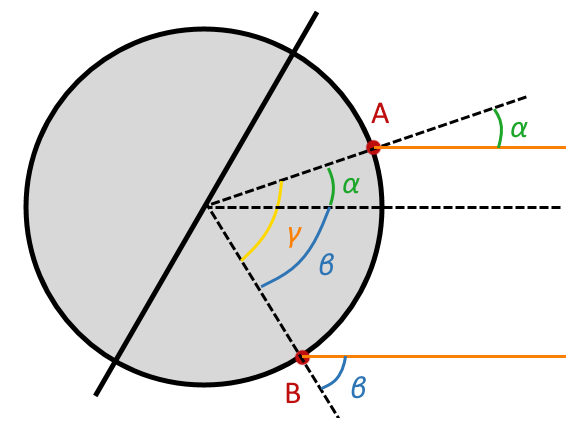
4. On considère maintenant deux points A et B situés sur le même méridien B étant au sud de A. A et B sont situés de part est d’autre du tropique nord. Au midi solaire, le 21 juin, les rayons du soleil arrivent en A inclinés avec un angle $*\alpha*$ par rapport à la verticale, et en B avec un angle $*\beta*$ par rapport à la verticale. Que vaut l’angle $*\gamma*$ formé par les rayons de la Terre passant par A et B ?
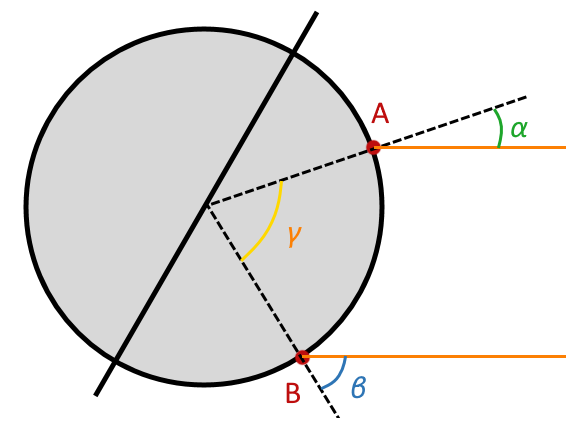
Correction
1. Schéma de la situation
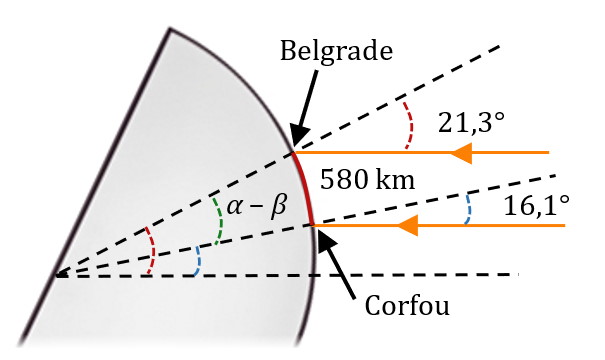
2. On remarque que cet angle vaut $*\alpha - \beta*$.
3. $* L = r·(\alpha \; – \beta)*$, avec $*r*$ le rayon de la Terre et $*L*$ la distance Belgrade - Corfou.
$*\alpha*$ = 0,3718 radian
$*\beta*$ = 0,2810 radian
donc $*r*$ = 580÷(0,3718 – 0,2810) ≃ 6388 km.
4. On voit sur le schéma ci-dessous que $*\gamma = \alpha + \beta*$
Mesure d’un méridien par triangulation
En 1792, Delambre et Méchain ont pour mission de mesurer précisément la longueur d’une portion de méridien (arc de cercle reliant les deux pôles) pour pouvoir en déduire ensuite la longueur totale d’un méridien.

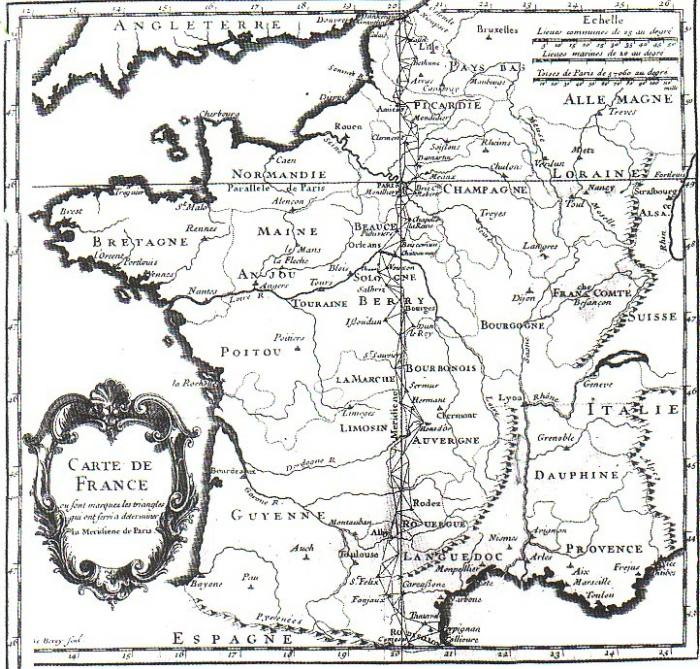
Pour mesurer la portion de méridien reliant Dunkerque à Barcelone, ils se servent d’une méthode appelée triangulation, qui s’appuie sur la propriété suivante des triangles :
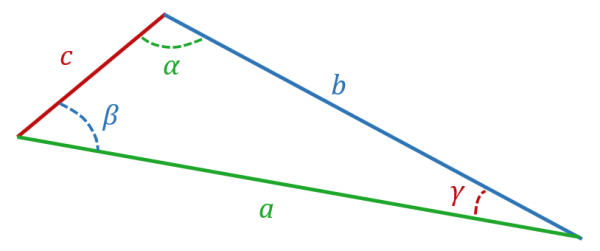
$µ \frac a{\sin \alpha} = \frac b{\sin \beta} = \frac c{\sin \gamma} µ$
Cette relation est valable pour tous les triangles. Ainsi, si on connaît la longueur d’un côté ainsi que la valeur des deux angles qui lui sont associés (par exemple, $*c*$, $*\alpha*$ et $*\beta*$), on peut en déduire les deux autres longueurs du triangle.
On rappelle par ailleurs que la somme des angles d’un triangle mesure 180°.
Mesure par triangulation
À partir du schéma ci-dessous, déterminer la longueur AE.
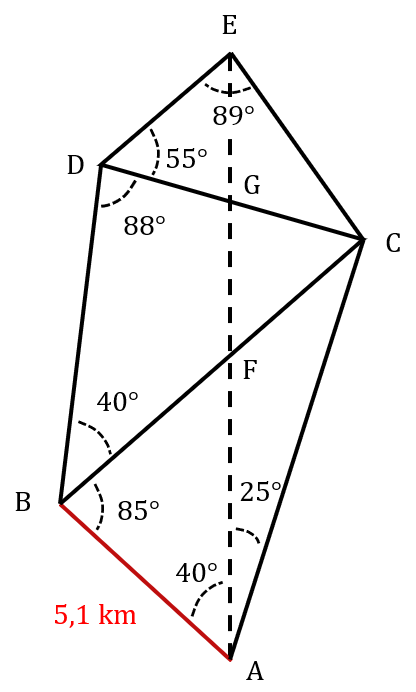
Correction
Il faut commencer par calculer les angles manquants, puis calculer les longueurs nécessaires.
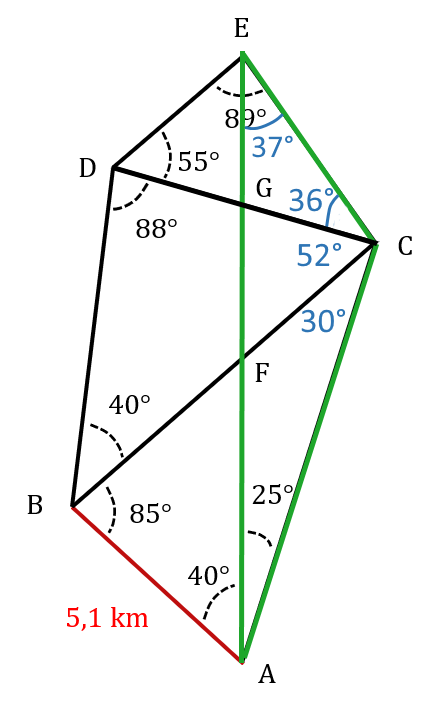
On commence par la longueur AC dans le triangle ABC : $µ \begin{aligned} \frac {\mathrm{AC}}{\sin 85°} &= \frac {5,1}{\sin 30°} \\ \mathrm{AF} &= \frac {5,1}{\sin 30°}×\sin 85° \end{aligned} µ$
On en déduit que AC = 10,2 km
Ensuite, on se place dans le triangle ACE : $µ \begin{aligned} \frac {\mathrm{AE}}{\sin 118°} &= \frac {\mathrm{AC}}{\sin 37°} \\ \mathrm{AE} &= \frac {\mathrm{AC}}{\sin 37°}×\sin 118° \end{aligned} µ$ On trouve AE = 14,9 km.
On peut faire différemment, mais c’est plus compliqué ! 😊
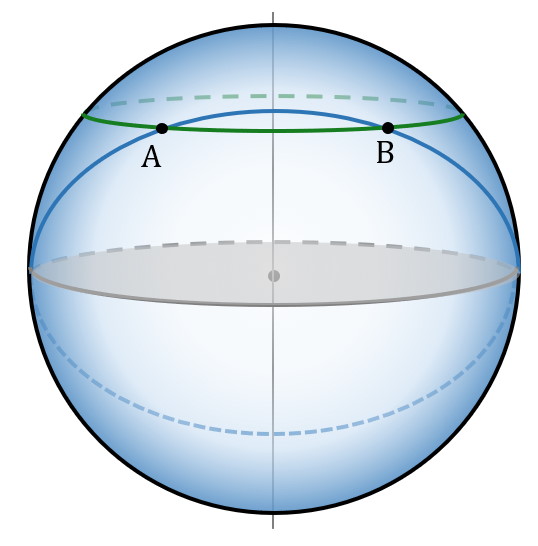
Se repérer sur une sphère
- Calculer la longueur d’un arc de méridien et d’un arc de parallèle.
- Comparer, à l’aide d’un système d’information géographique, les longueurs de différents chemins reliant deux points à la surface de la Terre.
Latitude & longitude
Pour se repérer sur Terre, on la découpe « horizontalement » (du nord au sud) par des cercles parallèles à l’équateur appelés « parallèles ».
On la découpe aussi « verticalement » par des demi-cercles qui joignent le pôle nord et le pôle sud : les méridiens.
On repère un point à la surface de la Terre par deux coordonnées angulaires (c’est-à-dire que ces coordonnées sont des angles), sa latitude et sa longitude. Ces deux coordonnées sont définies à partir de deux références : l’équateur pour la latitude et le méridien de Greenwich pour la longitude.
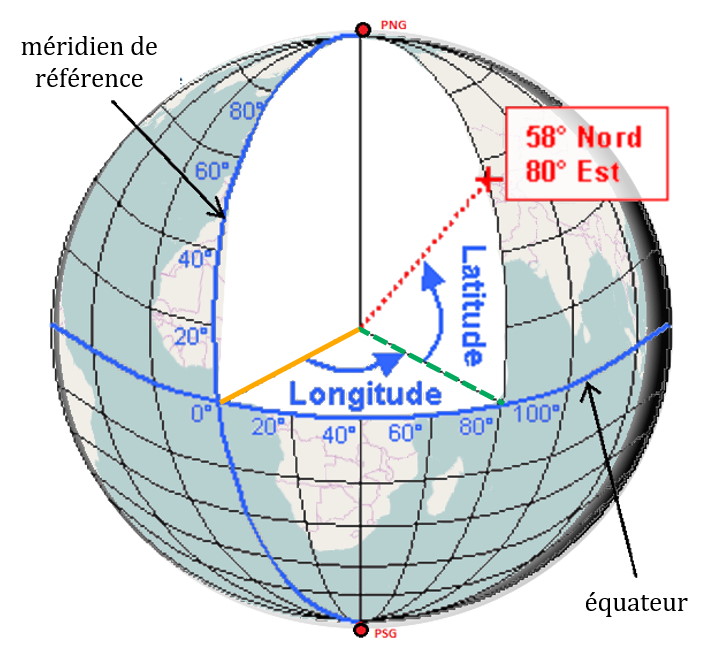
Latitude d’un lieu X : angle entre le rayon passant par X (en rouge) et le rayon passant par l’équateur au même méridien (en vert).
Longitude d’un lieu X : angle entre le rayon passant par l’intersection du méridien où se trouve X et l’équateur (en vert) et le rayon passant par le méridien de Greenwitch et l’équateur (en orange).
Distance entre deux points à la surface de la Terre
Arc de parallèle
À la latitude $*\theta*$ correspondant au cercle vert sur la figure ci-dessous, faire le tour de la Terre est plus court qu’au niveau de l’équateur.
En effet, le rayon $*R_L*$ de ce cercle est plus petit que le rayon de la Terre $*R_T*$.
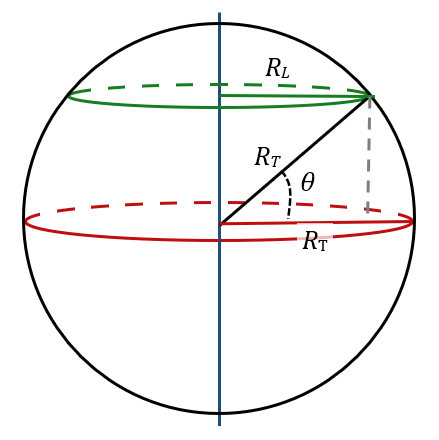
Un petit peu de géométrie de niveau collège permet de montrer que $*R_L = R_T·\cos \theta*$ ou encore $*R_L = R_T·\sin (90 - \theta)*$
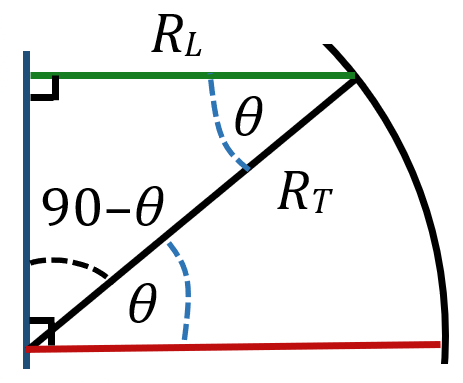
Arc de parallèle
Coordonnées de Belgrade : 44,8° N ; 20,5° E
Coordonnées de Bordeaux : 44,8° N ; 0,6° O
1. Calculer l’arc de parallèle entre Belgrade et Bordeaux.
2. Même question pour Oslo (60°N, 10°E) et St Pétersbourg (60°N, 30°E).
Correction
1. Le rayon du cercle décrivant le parallèle 44,8° N vaut $*R_L = R_T·\cos 44,8° =*$ 4527 km.
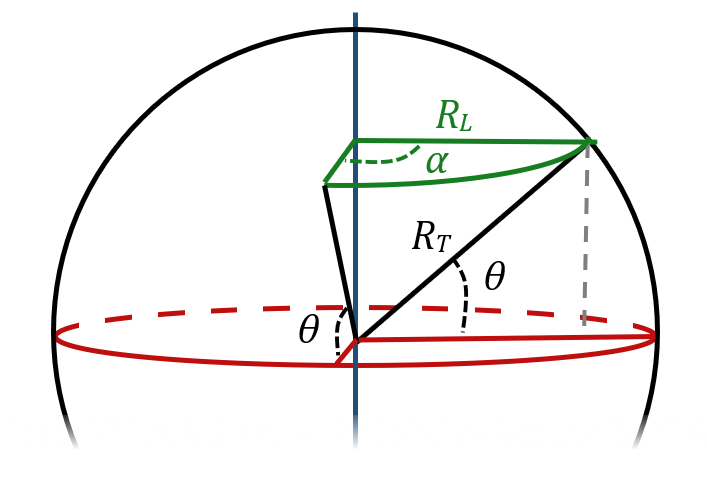
N’oubliez pas que Bordeaux se trouve à 0,6° Ouest alors que Belgrade se trouve à 10,5° Est
Dans cette situation, $*\alpha*$ = 21,1° = 0,368 rad (ne pas oublier de convertir en radian !) et $*R*$ = 4527 km.
D’où $*\ell = R·\alpha = 4527×0,368*$ ≃ 1667 km
2. Oslo – St Pétersbourg : 1114 km
Distance entre deux points à la surface de la Terre
Le plus court chemin entre deux points A et B à la surface de la Terre est l’arc du grand cercle qui les relie. Autrement dit, l’arc du cercle ayant pour centre le centre de la Terre et sur lequel se trouvent les deux points (en bleu).
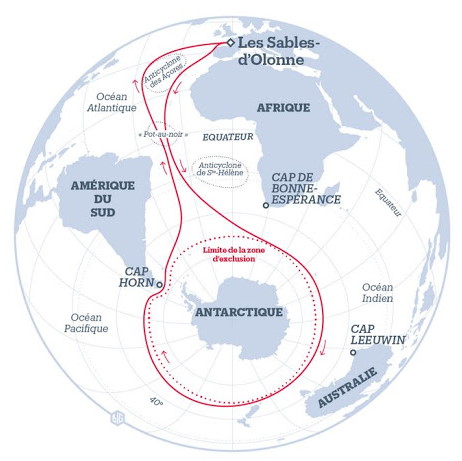
Vol Londres – New York
Expliquer pourquoi, lors d’un vol Londres – New York, l’avion suit la trajectoire en bleue et non la trajectoire en rouge sur l’image ci-dessous.
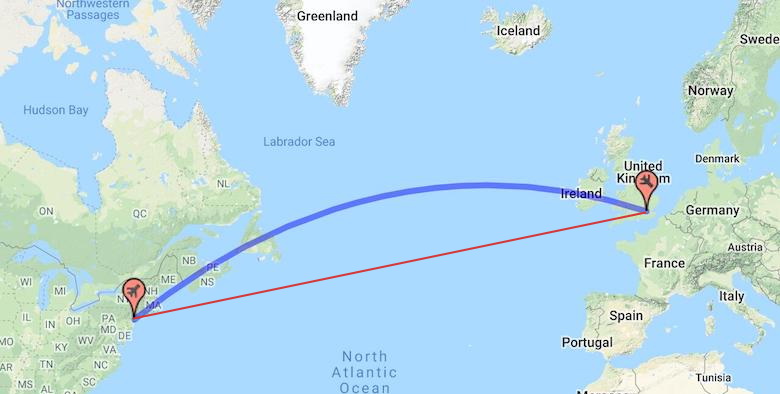
Correction
Le trajet en bleu représente la ligne droite à la surface de la Terre. Sur une carte, cette surface est déformée (car on projette sur une surface plane – la surface de la carte – une surface qui en réalité de l’est pas – la surface de la Terre.)
Donc ce qui semble être rectiligne sur la carte (le trajet en rouge) ne l’est pas en réalité.
Révision & entraînement
La sphéricité de la Terre (E3C)
Dans tout l’exercice, la Terre est assimilée à une sphère de rayon 6371 km.
1. Repérage sur la sphère terrestre
Afin de se repérer à la surface de la sphère terrestre, on utilise des coordonnées géographiques (longitude, latitude).
| Ville | Pays | Longitude | Latitude |
|---|---|---|---|
| Libreville | Gabon | 9° Est | 0° |
| Quito | Équateur | 79° Ouest | 0° |
| Toronto | Canada | 79° Ouest | 44° Nord |
| Toulouse | France | 1° Est | 44° Nord |
1. Calculer la longueur d’un méridien terrestre.
À partir des informations du tableau ci-dessus :
2.a. Indiquer les villes qui sont situées sur un même méridien.
2.b. Indiquer les villes qui sont situées sur un même parallèle.
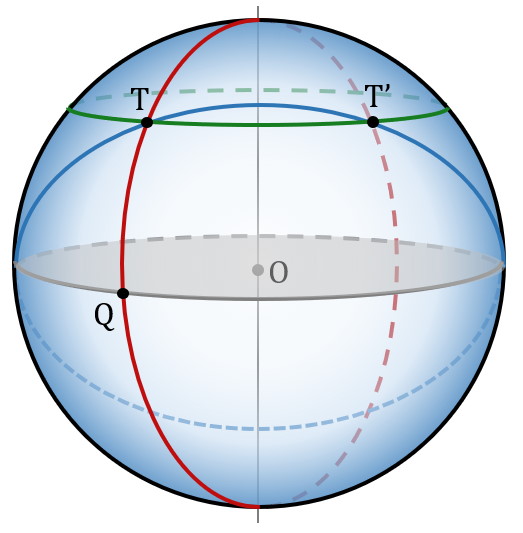
On note O le centre de la Terre et T, Q et T’ les villes Toronto, Quito et Toulouse. On note I le centre du parallèle passant par Toronto et Toulouse. Sur le schéma ci-dessous (figure 1a) représentant la sphère terrestre, on a placé les points O, I, Q, T et T’.
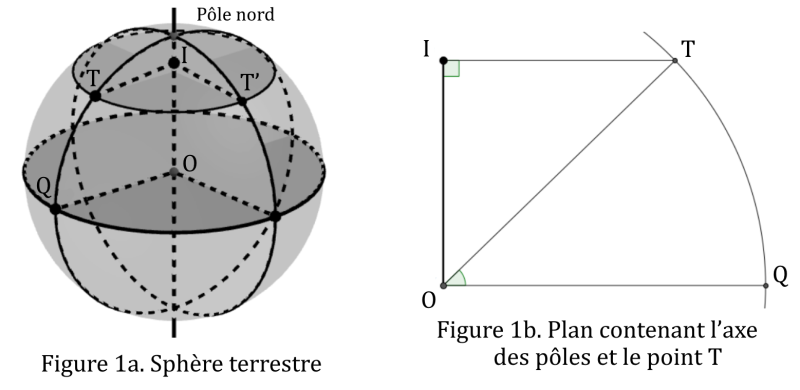
3.a Donner la mesure, en degré, des angles QOT et TIT’.
3.b Calculer la longueur de la portion de méridien reliant Quito à Toronto.
À l’aide de la figure 1b :
4.a. Préciser la longueur OT puis calculer la longueur IT.
4.b. En déduire la longueur du parallèle passant par Toulouse et Toronto.
4.c. Justifier, par un calcul, que la longueur de la portion de parallèle reliant Toulouse à Toronto est environ égale à 6399 km.
5. Un système d’information géographique (SIG) donne les informations suivantes :
• Distance Quito - Toronto : 4891 km
• Distance Toulouse - Toronto : 6230 km
Pour un système d’information géographique, la distance entre deux points du globe est le plus court chemin qui les relie à la surface de la Terre.
Expliquer pourquoi les longueurs données par le SIG et celles calculées dans les questions 3 et 4 sont, dans un cas, très proches alors que, dans l’autre, elles ne le sont pas.
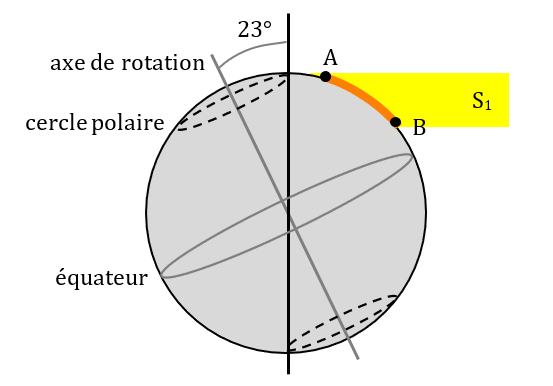
2. les différents climats de la Terre
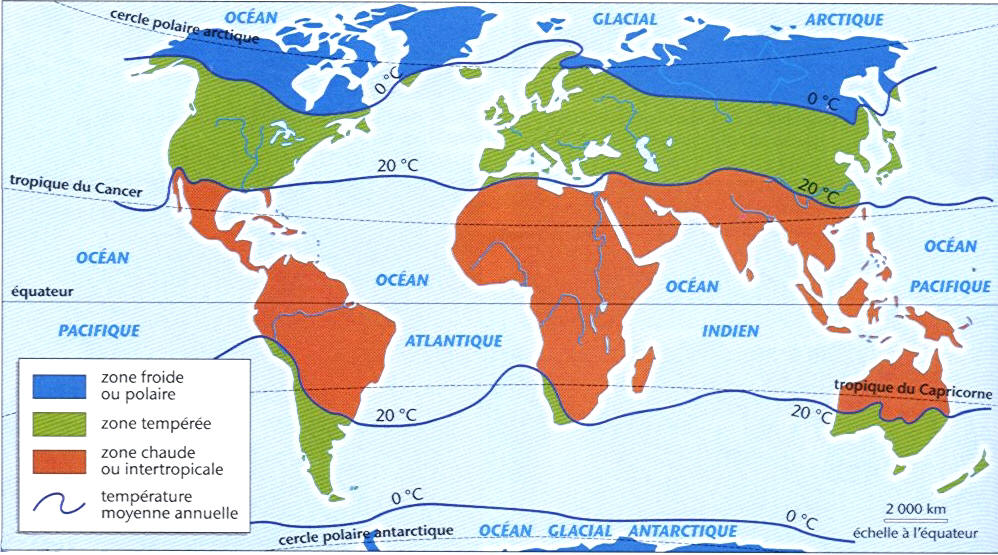
Sur cette carte, on constate que Quito et Libreville, qui sont à la même latitude, sont dans une zone chaude intertropicale. Pour Toronto, situé à la même longitude que Quito, la température moyenne annuelle est plus froide.
Afin d’expliquer ces différences climatiques, un élève a proposé comme hypothèse :
« Il fait plus chaud à l’équateur qu’aux pôles parce que La Terre est plus proche du Soleil à l’équateur qu’aux pôles ».
6. À partir des connaissances acquises et des informations issues des documents ci-dessous, rédiger un paragraphe argumenté permettant à la fois d’expliquer qu’il fait plus chaud à l’équateur qu’aux pôles et d’invalider l’hypothèse émise par cet élève.
La justification des arguments pourra s’appuyer sur des schémas explicatifs.
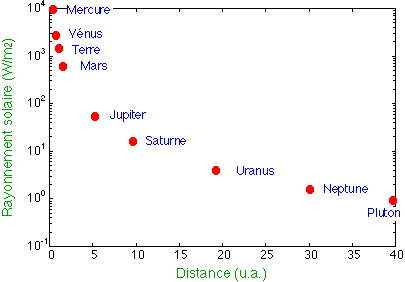
Remarque : 1 unité astronomique (ua) = 1,5×108 km

| Latitude | 0° | 45° nord | 60° nord | 89° nord |
| Lieu correspondant à la latitude | Quito | Bordeaux | Oslo | Pôle nord |
| Surface recevant une même quantité d’énergie (m2) | 1 | 1,4 | 2 | 57 |
| Puissance solaire reçue en moyenne par unité de surface (W/m2) | 420 | 420÷1,4 = 300 | 420÷2 = 210 | 420÷57 = 7,36 |
Correction
1. Un mériden est un demi-cercle allant d’un pôle à l’autre de la Terre. Sa longueur est donc $*\pi R_T*$ ≃ 20.000 km
2.a. Un méridien est repéré par sa longitude. Donc Quito et Toronto sont sur le même méridien.
2.b. Un parallèle est repéré par sa latitude. Donc Toronto et Toulouse sont sur le même parallèle, de même que Quito et Libreville.
3.a. $*\widehat{QOT}*$ = 44° et $*\widehat{TIT’}*$ = 79 + 1 = 80°
3.b. Il faut d’abord convertir l’angle $*\widehat{QOT}*$ en radian : 44° = 0,768 radian. Donc la longueur de la portion de méridien vaut $*R_T*$×0,768 = 4893 km.
4.a. OT est le rayon de la Terre. L’angle $*\widehat{OTI}*$ vaut 44°.
Vous pouvez calculer la longueur IT en trouvant un des angles non droit du triangle OIT, en vous servant ou bien de la « règle des angles alternes-interne » ou en remarquant que l’angle $*\widehat{QOI}*$ est droit.
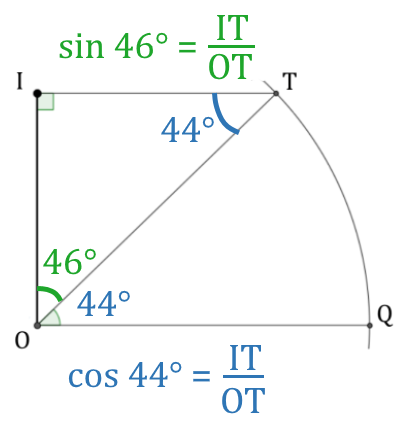
Donc IT = $*R_T*$×cos(44°) = $*R_T*$×sin(46°) = 4583 km.
4.b. Il s’agit de la circonférence du cercle de rayon $*R*$ = 4583 km soit 2π×4583 = 28.795 km.
4.c. Il s’agit de l’arc de cercle de rayon $*R*$ = 4583 km et d’angle $*\widehat{TIT’}*$ = 80° = 1,396 radian. Donc cette longueur vaut $*R·\widehat{TIT’}*$ = 6399 km.
5. La longueur la plus courte entre deux points sur une sphère est l’arc du grand cercle qui les relie.
Le méridien qui relie Toronto à Quito, c’est la moitié d’un grand cercle, celui en rouge sur le schéma. Donc la distance qu’on a calculée à la question 3.b est bien la distance la plus courte.
Pour la distance de Toulouse à Toronto, nous avons calculé la portion de parallèle passant de l’un à l’autre (en vert). Un parallèle n’est pas un grand cercle. La distance la plus courte entre Toulouse et Toronto est la portion du grand cercle représenté en bleu. C’est pour cette raison que la distance donnée par le SIG (qui est la distante la plus courte) est différente de celle qu’on a calculée.
6. La différence de distance entre Quito et le Soleil d’une part, et Toronto et le Soleil d’autre part, est très faible devant la valeur de ces distances. De plus, cela n’explique pas pourquoi la température à Toronto varie grandement entre l’été et l’hiver.
Cette différence de température s’explique par la différence d’inclinaison des rayons du Soleil lorsqu’ils arivent à Quito et à Toronto. Le tableau nous montre qu’à 45° de latitude, la puissance moyenne des rayons solaires reçue est 1,4 fois plus faible qu’à l’équateur. Ceci est également illustré sur les deux photos montrant l’éclairage à l’équateur et près du pôle nord.
C’est cette différence d’inclinaison des rayons solaires, et donc de puissance solaire surfacique, qui explique la différence de climat entre Quito et Toronto.
New York – Pékin en avion (E3C)
Cet exercice a été donné en devoir en 2020/2021
Les constructeurs d’avions ayant fait de grandes améliorations en matière de sécurité sur leurs biréacteurs, les autorités américaines de l’aviation civile ont revu fin décembre 2011 la réglementation sur ces avions, en les autorisant à voler au-dessus du Pôle Nord.
Ce sujet étudie les durées de vol sur le trajet New York-Pékin en fonction de deux trajectoires possibles : soit le long du 40e parallèle, soit en passant par le Pôle Nord.
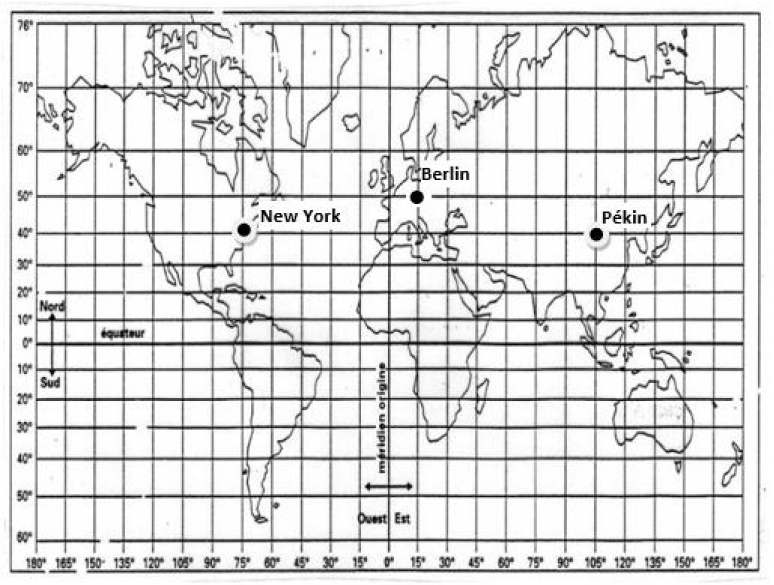
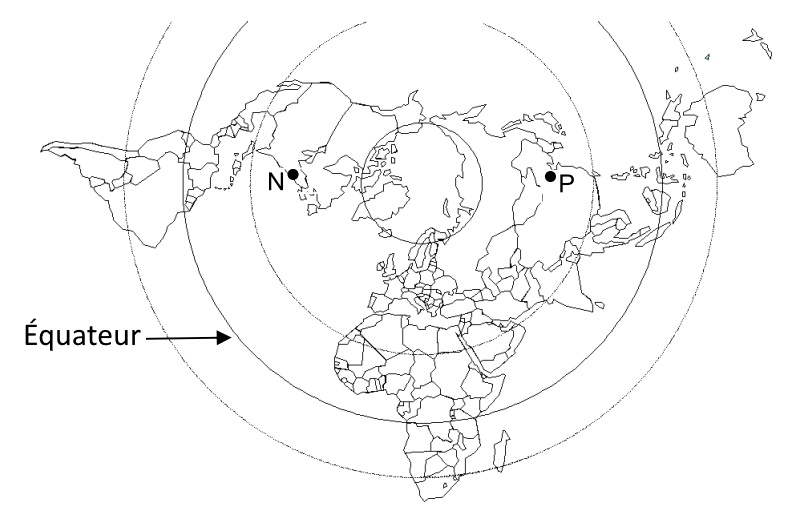
Document 1 : deux planisphères – deux représentations de la Terre
Document 2 : représentation de la Terre pour l’étude du trajet en passant par le Pôle Nord
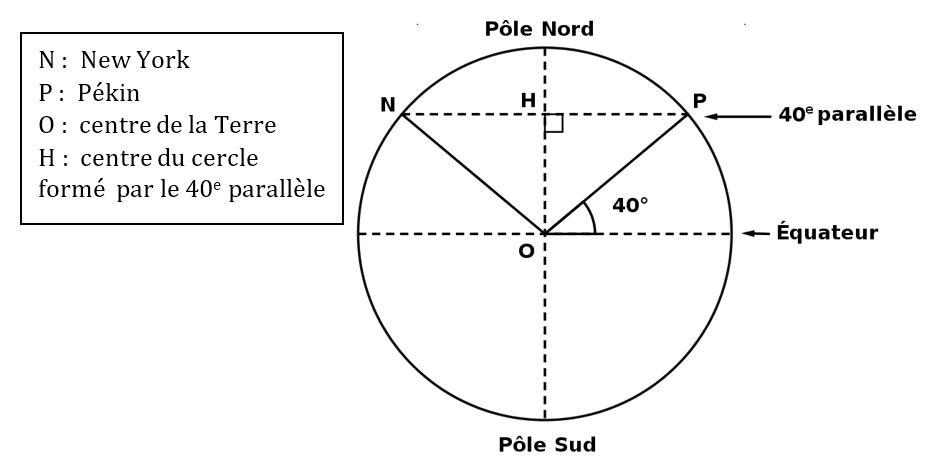
Calcul de la longueur d’un méridien
1. Le rayon de la Terre est de $*R_T*$ = 6380 km. Quelle est la longueur d’un méridien ?
Trajet New York – Pékin en suivant le 40e parallèle
Jusqu’au début des années 2010, la liaison aérienne New York – Pékin à bord d’avions biréacteurs suivait une route relativement proche de la ligne du 40e parallèle.
2. Tracer, sur la figure 1b, un des deux arcs de parallèle qui relie New York à Pékin.
3. D’après le document 1 – figure 1a, indiquer les coordonnées terrestres (latitude, longitude) de chacune des villes de New York et de Pékin. Il est attendu des coordonnées entières.
4. En utilisant les coordonnées de New York et de Pékin, montrer que chacun des arcs de parallèle reliant New-York à Pékin est un demi-cercle.
5. Calculer la distance New York – Pékin le long du 40e parallèle.
Trajet New York – Pékin en passant par le Pôle Nord
Depuis décembre 2011, les avions biréacteurs peuvent survoler le pôle Nord.
6. Tracer, sur la figure 1b, la route que les avions biréacteurs sont autorisés à emprunter entre New York et Pékin en passant par le Pôle Nord.
7. Montrer que la distance New York – Pékin par la route polaire mesure environ 11 100 km.
Correction
1. Méridien = demi-cercle de pôle à pôle. Longueur d’un méridien = $*\pi R_T*$ ≃ 20.000 km
2. Arc de parallèle : un des deux demi-cercles en bleu
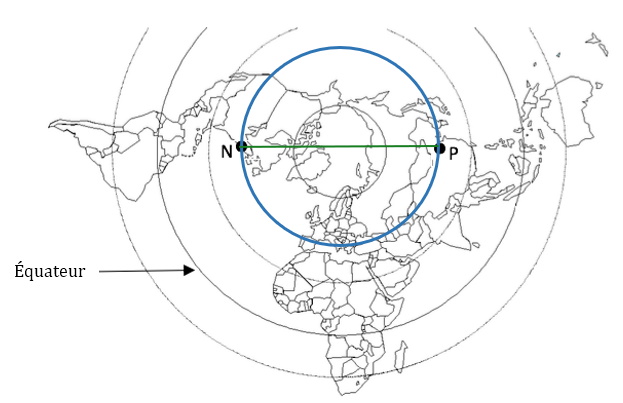
3. Pékin : 40°N – 105°E et New-York : 40°N – 75°O
4. La différence de longitude entre les deux villes est de 180°, mais elles se situent à la même latitude. Les arcs de parallèle qui les relient sont donc des demi-cercles.
5. Diamètre du 40e parallèle : il faut d’abord calculer son rayon. $*R*$ = *$R_T·cos(40°)*$ ≃ 4890 km.
Donc la longueur du parallèle reliant Pékin à New York est : 4890×π = 15350 km.
6. Voir schéma
7. En passant par le pôle nord, on parcourt un arc de cercle dont le rayon est égal au rayon de la Terre et dont l’angle vaut $*\theta*$ = 2×(90-40) = 100°.
La longueur de cet arc de cercle vaut $*\ell*$ = *$R_Tθ*$ = 11.135 km soit environ 11.100 km.