4.1 Le son, phénomène vibratoire
Le son est omniprésent dans notre environnement. Il est même, la plupart du temps, une nuisance, de part son intensité comme de sa « qualité ». Dans ce chapitre, on va s’intéresser à différents aspects du son dans sa dimension physique (et non pas musicale, ça sera pour plus tard).
Son pur et son composé
Qu’est-ce que le son ?
Le son, c’est une vibration de l’air (ou plus généralement du milieu matériel dans lequel le son se propage, car le son ne se propage pas que dans l’air…) qui se propage. Les ondes sonores font partie de la grande famille des ondes mécaniques, c’est-à-dire des ondes liées à une déformation de la matière.
Un son (ou onde sonore) est produit par une perturbation qui fait se déplacer la matière de part et d’autre de sa position d’équilibre. C’est une onde périodique (pas forcément sinusoïdale) de fréquence comprise entre 20 Hz et 20 kHz (en dehors de ces limites, il s’agit d’infrason ou d’ultrason.

Cette perturbation va créer des zones de plus forte densité de particules (haute pression) et des zones de plus faible densité de particules (faible pression).
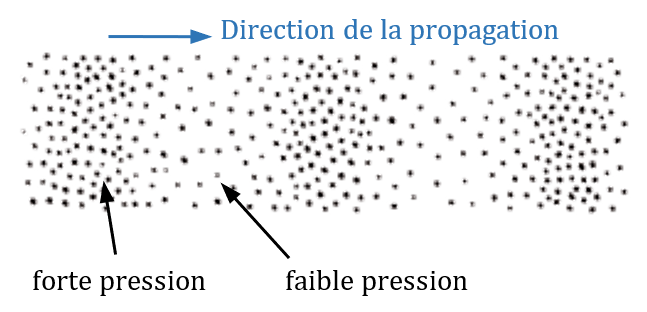
Visualiser et créer un son
- Utiliser un logiciel permettant de visualiser le spectre d’un son.
- Utiliser un logiciel pour produire des sons purs et composés.
Objectif : visualiser le spectre d’un son produit par un diapason et par une flûte. Créer un son pur. Créer un son composé.
Pour réaliser ces expériences, nous nous servirons d’Audacity un logiciel open source d’édition et de traitement du son.
Éléments de réponses
Son pur
Un son est dit « pur » en physique, si la vibration des molécules du milieu de propagation est sinusoïdale. Un son pur est associé à un signal temporel sinusoïdale. Par exemple, si on mettait un détecteur de pression en un point où passe une onde sonore pure, la pression qu’il enregistrerait serait une fonction sinusoïdale du temps.

Son complexe
Un son composé, aussi appelé son complexe, est associé à un signal périodique non sinusoïdal.

En fait, les sons « musicaux », c’est-à-dire les sons dont la fréquence est bien définie, sont des sons complexes, pour des raisons qui dépassent largement le cadre de ce cours. Notre voix, le son d’un instrument de musique, tous ces sons sont complexes.
Un tel signal, de fréquence $*f*$ se décompose en une somme de signaux sinusoïdaux de fréquences multiples de $*f*$. La fréquence $*f*$ est appelée fréquence fondamentale, les autres fréquences sont appelées harmoniques.
Le spectre d’un son est un graphique qui montre l’importance des différentes fréquences composant une onde sonore.

On en déduit quelles sont les harmoniques présentes dans la fonction et quelles sont leurs amplitudes relatives.
Un son pur est une sinusoïde, son spectre est donc constitué d’une seule harmonique.
Un son complexe possède un spectre présentant plusieurs harmoniques.
Intensité et niveau sonore
- Relier puissance sonore par unité de surface et niveau d’intensité sonore exprimé en décibels.
Intensité sonore
Une source sonore est caractérisée par la puissance sonore $*P*$ qu’elle émet, en watt.
Cette puissance est émise dans toutes les directions, transportée par l’onde sonore, et se « dilue » sur la surface de la sphère d’émission qui grandit à mesure que le son se propage (on suppose que cette puissance est émise de manière égale dans toutes les directions de l’espace – dans la pratique, c’est rarement le cas).
L’intensité $*I*$ d’un son correspond une puissance sonore par unité de surface. $*I*$ s’exprime en W·m-2. Plus on se trouve loin de la source, plus l’intensité sonore perçue est faible.
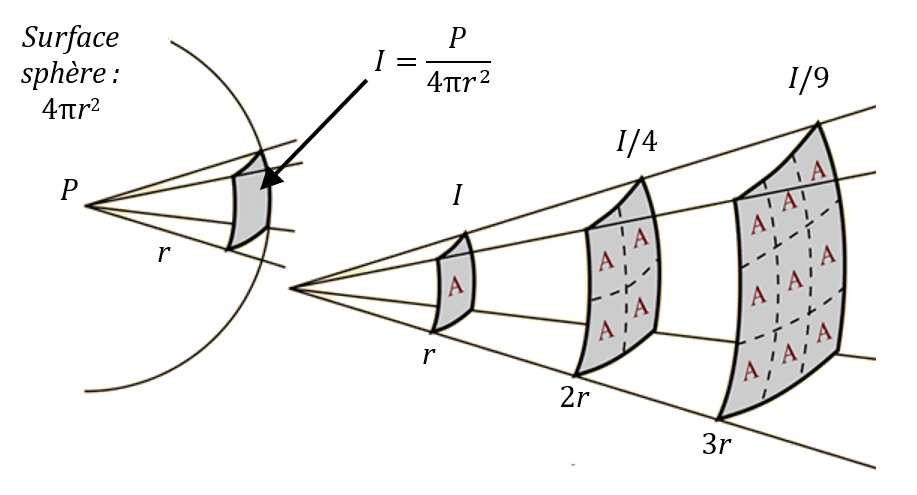
Lorsqu’on se trouve à une distance $*r*$ de la source, la puissance sonore $*P*$ est répartie sur une surface de $*4\pi r^2*$.
Lorsqu’on se trouve à une distance deux fois plus grande, la même puissance est répartie sur une surface 4 fois plus grande $*4\pi (2r)^2*$. L’intensité sonore est donc 4 fois plus faible.
Puissance & intensité sonore
Un haut-parleur émet un son avec une puissance $*P*$ = 0,5 W.Quelle sera l’intensité sonore perçue à 1 m ? À 10 m ?
Correction
À 1 m : $*I = \frac {0,5}{4\pi·1^2}*$ ≃ 0,04 W·m-2À 10 m : $*I = \frac {0,5}{4\pi·10^2}*$ ≃ 4·10-4 W·m-2
Niveau sonore
L’intensité sonore ne reflète cependant pas la perception « biologique » qu’on peut avoir d’un son. Pour le dire de manière approximative, si vous doublez l’intensité d’un son, vous n’aurez pas l’impression que le son est « deux fois plus fort ». C’est parce que la perception d’un son est « logarithmique ». Autrement dit, vous aurez une impression de son « deux fois plus fort » si le logarithme de l’intensité sonore a doublé. C’est pour ça qu’on a définit, en plus de l’intensité sonore (noté $*I*$), le niveau sonore (noté $*L*$).
Le niveau sonore $*L*$ d’un son d’intensité $*I*$ s’exprime en décibel (dB) et se calcule grâce à la relation suivante :
| $µ L = 10·\log \left( \frac I{I_0} \right)µ$ |
$*L*$ : niveau sonore (dB) $*I*$ : intensté sonore (W·m-2) $*I_0*$ : intensité sonore de référence (10-12 W·m-2) |
$*I_0*$ correspond plus ou moins au son le plus faible qui soit perceptible (mais ça dépend de la fréquence du son et des capacités auditives de la personne, bien sûr).
Pour calculer l’intensité sonore connaissance le niveau sonore, on utilise la relation suivante.
| $µ I = I_0·10^{\frac L{10}}µ$ | $*L*$ : niveau sonore en dB $*I*$ : intensité sonore en W·m-2 $*I_0*$ : intensité de référence = 10-12 W·m-2 |
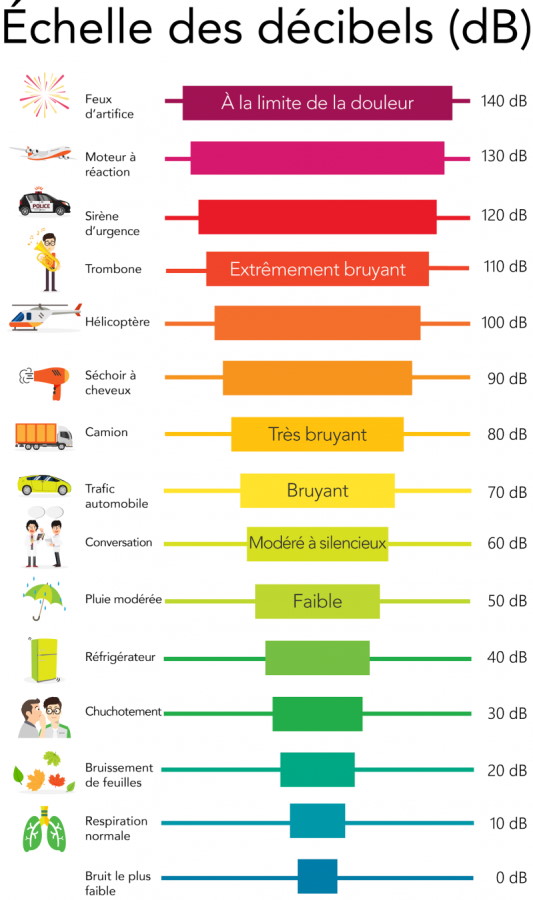
À partir de 85 dB, la loi estime qu’une durée d’exposition prolongée peut présenter un risque pour l’audition. Ce risque est d’autant plus grand que la durée d’exposition est grande (5 h par semaine à 89 dB, 1h45 par semaine à 100 dB).
Niveau sonore
1. Un haut-parleur émet un son avec une puissance $*P*$ = 0,5 W.
Quel sera le niveau sonore perçu à 1 m ? À 10 m ?
2. Si on ajoute un deuxième haut-parleur juste à-côté du premier, celui-ci ayant la même puissance de 0,5 W, que sera le niveau sonore à 1 m ? À 10 m ?
Correction
1. On a calculé dans l’exercice précedent que $*I*$ = 0,04 W·m-2 à 1 m, donc $*L = 10\log \frac {4·10^-2}{10^{-12}} = *$ 106 dB
À 10 m, $*I*$ = 4·10-4 W·m-2 à 1 m, donc $*L*$ = 86 dB
2. Il ne faut surtout pas multiplier le niveau sonore par deux, car les niveaux sonores ne s’ajoutent pas et ne se multiplient pas. Il faut toujours passer par les intensités sonores. Avec un deuxième haut-parleur, $*I*$ = 0,04×2 = 0,08 W·m-2. Donc $*L*$ = 109 dB.
À 10 m, on trouve $*L*$ = 89 dB
Instruments de musique
- Relier qualitativement la fréquence fondamentale du signal émis et la longueur d’une corde vibrante.
La plupart des instruments produisent des sons grâce à des cordes (instruments à cordes) ou des colonnes d’air en vibration (instruments à vent).
Instruments à corde
Une corde tendue émet en vibrant un son composé dont la fréquence fondamentale $*f*$ ne dépend que de ses caractéristiques : longueur $*L*$, tension $*T*$, masse linéique $*\mu*$).
$µ f = \frac 1{2L}\sqrt{\frac T\mu} µ$Instrument à vent
Dans les instruments à vent, un phénomène analogue se produit par vibration de l’air dans un tuyau.
La fréquence du son produit par une colonne d’air est inversement proportionnelle à sa longueur.
La guitare
La corde la plus grave sur une guitare doit être accordée pour produire un mi (mi2) de fréquence 82,41 Hz.
Quelle sera la fréquence de la note produite en pinçant la corde de la guitare exactement en son milieu ?