4.3 Le son, une information à coder
Un son est codé par une suite de 0 et de 1 en informatique. Comment passe-t-on d’un son à cette suite binaire ?
Numérisation d’un son
- Justifier le choix des paramètres de numérisation d’un son.
- Estimer la taille d’un fichier audio.
Chaîne d’acquisition
Comme nous l’avons vu au chapitre 4.1, un son est une variation de pression au cours du temps.
C’est un signal analogique, c’est-à-dire un signal qui varie de manière continue au cours du temps (une fonction continue, si vous voulez).
Lorsqu’un micro reçoit un son, la variation de pression atmosphérique au point où il se trouve ressemble à quelque chose comme la courbe ci-dessous
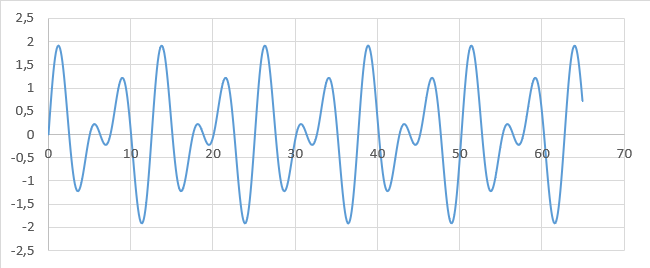
La numérisation d’un son passe par une première étape qui est sa transformation en signal électrique analogique par le microphone. Puis le signal électrique délivré par le microphone est numérisé par la carte son.

Le signal numérique est une suite de nombres qui ne peuvent prendre que des valeurs discrètes (c’est-à-dire un ensemble de valeurs prédéfinies, pas n’importe quelle valeur).
Paramètres de la numérisation
Fréquence d’échantillonnage
Pour numériser le signal analogique, la carte son effectue une mesure de ce signal à intervalle de temps régulier. On dit qu’elle fait un échantillonnage. Le nombre de mesures réalisées chaque seconde est appelée la fréquence d’échantillonnage.
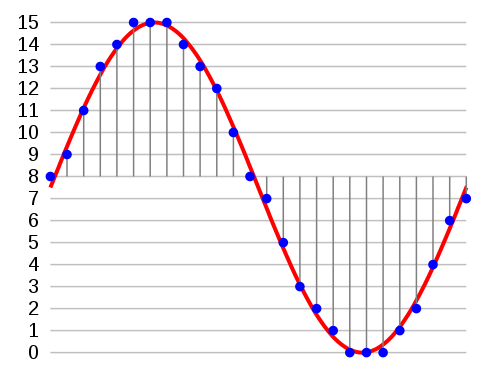
Sur le graphique ci-dessus, chaque trait noir représente une mesure. Plus la fréquence d’échantillonnage est élevée, mieux ces mesures suivront l’évolution de la tension analogique (la numérisation sera plus fidèle) mais plus il y aura de valeurs à traiter chaque seconde (nécessitant des ressources processeur et mémoire plus importantes).
Comment les ordinateurs manipulent l’information
À lire avant le paragraphe suivant sous peine de ne rien comprendre
Les ordinateurs manipulent l’information exclusivement sous forme de bits qui peuvent prendre la valeur 0 ou la valeur 1. Pour qu’un ordinateur comprennent un nombre, il faut qu’il sache comment celui-ci est codé sous forme de bit. Sans entrer dans les détails (il existe de nombreux formats de codage, selon que l’on veuille coder un entier ou un réel, un nombre positif ou un nombre qui peut être positif ou négatif…), il faut lui préciser avec combien de bits ce nombre est codé.
Une information codée sur 1 bit ne pourra prendre que deux valeurs (0 ou 1). Une information codée sur deux bits pourra prendre 4 valeurs (00, 01, 10 , 11). Une information codée sur n bits pourra prendre 2n valeurs.
Plus le nombre de bits utilisés par l’information est grand, plus cette information prendra de ressources processeur et mémoire pour être traitée et stockée.
Résolution de la numérisation
La valeur mesurée au moment de l’échantillonnage est une information (un nombre). Une fois numérisée, elle ne peut prendre qu’un nombre fini de valeurs (par exemple 256 valeurs si elle est codée sur 8 bits). Il s’ensuit que cette valeur ne peut pas toujours être convertie de manière exacte si elle ne correspond pas à une des 256 valeurs possibles. La carte son doit procéder à une approximation. Moins il y a de valeurs possibles, plus cette approximation peut être grande.
La résolution de la numérisation (aussi appelée format d’échantilonnage, ou profondeur de numérisation) est le nombre de bits sur lesquels la valeur est codée. Plus grande est la résolution, plus fidèlement est stockée l’information, mais plus elle est lourde à traiter et à stocker.
Pèse-personne numérique
Imaginons un pèse-personne numérique, capable de peser un poids compris entre 0 et 120 kg. On va s’intéresser dans cet exercice à la numérisation de la valeur de la masse pesée.
Imaginons dans un premier temps que le pèse-personne numérise la valeur de la masse pesée sur 4 bits.
1. Combien de niveau différents peut-on coder sur 4 bits ?
2. On suppose que ces niveaux sont répartis de manière équitable entre 0 et 120. Compléter le tableau ci-dessous.
| valeur binaire | masse (kg) | valeur binaire | masse (kg) |
|---|---|---|---|
| 0000 | 0 | ||
| 0001 | |||
| 0010 | |||
| 0011 | |||
| 0100 | |||
| 0101 | |||
| 0110 | |||
| 0111 | 1111 | 120 |
3. Quel est le « pas » de cette numérisation, c’est-à-dire l’écart, en kg entre deux niveaux consécutifs ?
4. En supposant que la valeur est arrondie au niveau le plus proche lorsqu’elle est numérisée, quelle valeur binaire prendra une masse de 45 kg ? Quel est l’imprécision générée par cette numérisation ?
5. Supposons maintenant que cette numérisation se fasse sur 8 bits au lieu de 4. Quelle est le pas de cette nouvelle numérisation ? Quel est l’avantage et quel est l’inconvénient d’une plus grande profondeur d’échantillonage ?
Correction
Le format « CD », un standard de numérisation du son
Le format « CD » correspond à une fréquence d’échantillonnage de 44,1 kHz (44100 mesures chaque seconde) codé sur 16 bits (soit 65536 valeurs possibles).
Une seconde au format CD correspond donc à 44100×16 = 705600 bits (à multiplier par deux s’il s’agit d’un son stéréo).
Conversion analogique numérique
Sur le graphique ci-dessous, on a représenté en bleu la tension amplifiée $*u_a(t)*$ issue d’un microphone et en rouge la tension $*u_n(t)*$ envoyée par la carte son à son module de conversion en binaire.
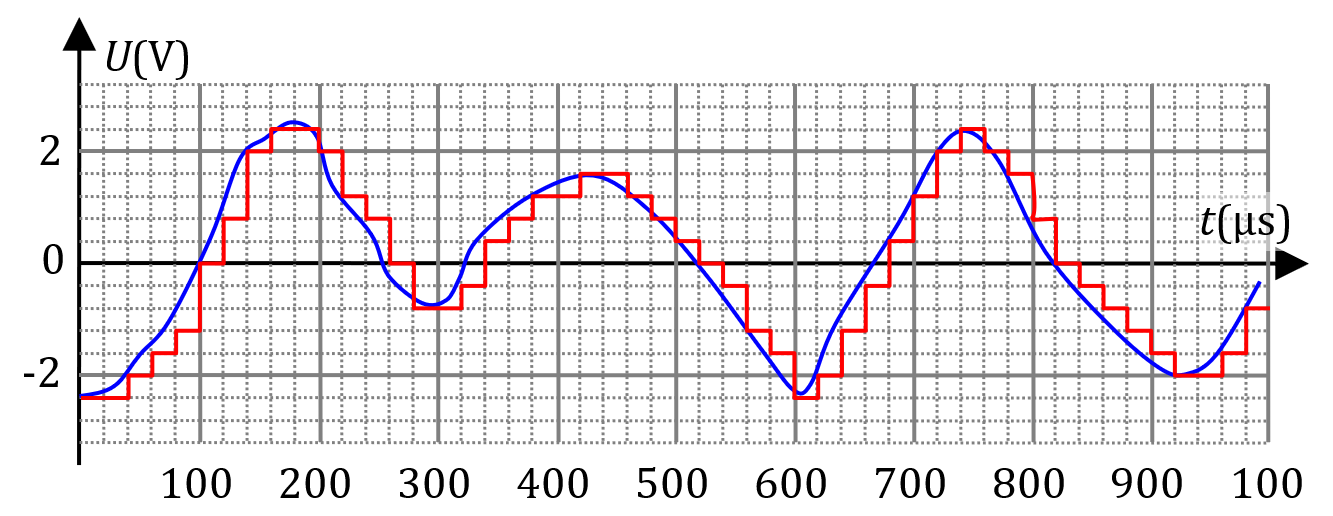
1. Les tensions $*u_a(t)*$ et $*u_n(t)*$ sont-elles numériques ou analogiques ? Justifier.
2. Combien de valeurs différentes peut prendre le signal $*u_n*$ sur ce graphique ? Combien de bits sont nécessaires pour coder cet ensemble de valeur ?
3. Déterminer la fréquence d’échantillonnage du convertisseur numérique-analogique.
4. Comment faudrait-il modifier les paramètres d’échantillonnage (profondeur et fréquence) pour que le signal $*u_n*$ se rapproche davantage de $*u_a*$ ?
Correction
Stockage d’un son
- Calculer un taux de compression.
- Comparer des caractéristiques et des qualités de fichiers audio compressés.
La taille d’un fichier est mesurée en octet : 1 octet (o) = 8 bits (soit 256 valeurs possibles).
Les multiples des octets peuvent être calculés de deux manières :
- la manière classique : 1 ko = 103 o ; 1 Mo = 106 o ; etc.
- la manière binaire : 1 kio = 210 o = 1024 o ; 1 Mio = 220 ko = 1 048 576 o ; etc.
Remarquez le « i » qui apparaît lorsqu’on exprime la taille en multiples binaire. On utilisera dans la suite du cours la manière classique.
Taille d’un fichier son non compressé
Format CD : 44,1 kHz ; 2 octets donc 44100×2 = 88 200 o/s soit 88,2 ko/s
Format « studio » : 192 kHz ; 3 octets donc 192 000×3 = 576 000 soit 576 ko/s
Ces valeurs sont données pour une piste. Pour de la musique en stéréo, il faut multiplier ces valeurs par deux (un son associé au canal gauche et l’autre associé au canal droit).
Taille d’un album de 45 minutes
1. Calculer la taille d’un fichier son non compressé contenant 45 minutes de musique stéréo au format CD.
2. Même question pour le format « studio »
Correction
1. 44 100(fréquence) ×2(2 octets) ×2(stéréo) ×60×45(durée en secondes) = 476 Mo
2. 192 000(fréquence) ×3(3 octets) ×2(stéréo) ×60×45(durée en secondes) = 3,1 Go
Compression d’un fichier son
À l’origine (milieu des années 80), avec la création des CD, les fichiers son n’étaient pas compressés.
La compression des fichiers son et leur décompression au moment de la lecture nécessite une puissance de calcul qui n’existait pas à cette époque.
Le format wav (un fichier du type titre_fichier.wav ) est un format non compressé.
Le problème de ces fichiers et qu’ils peuvent être très volumineux (plus de 300 Mo par heure, en son mono). Il faudra donc beaucoup d’espace mémoire pour les stocker et une connexion avec une bande passante importante pour les écouter en streaming.
C’est pour cette raison que sont apparus des formats de compression. Il en existe de deux types.
Taux de compression
C’est le pourcentage de volume mémoire perdu lors de la compression. Par exemple, si un fichier son non compressé fait 100 Mo et qu’après compression il ne fait plus que 20 Mo, le taux de compression est de 80 %.Compression avec perte (MP3, AAC…)
Lors de la compression, une quantité plus ou moins importante d’information est perdue. L’algorithme de compression est conçu de telle manière à ce que cette perte soit le moins audible possible.
Le taux de compression de ces formats est paramétrable par l’utilisateur. Plus ce taux est important, plus la perte de qualité sonore est importante. En MP3 par exemple, les taux de compression les plus courants sont de 128 kb/s, 256 kb/s et 320 kb/s.
Dans tout les cas, le rapport qualité/taille des formats compressés est bien supérieur aux formats non compressés. Par exemple, un son non compressé échantillonné à 22,1 kHz sur 2 octets (et qui occupe donc deux fois moins d’espace qu’un son en qualité CD) sera bien moins bon qu’un fichier son de qualité CD compressé avec un taux de compression de 50 %.
La différence entre les différents formats de compression réside dans leur statut « ouvert » ou « propriétaire » et dans leur capacité à avoir un meilleur rapport qualité/taille. Le format MP3 est le format dominant pour des raisons historiques et donc de compatibilité des lecteurs, mais ce n’est pas le meilleur (le meilleur pour le moment est le format OGG Vorbis).
Taux de compression d’un MP3
Une minute de musique stéréo au format MP3 128 kb/s occupe un espace d’environ 1 Mo. Calculer le taux de compression sachant que le fichier original était en qualité CD.
Correction
1 seconde en qualité CD non compressé : 88,2 ko ×2 (stéréo)1 minute de son stéréo en qualité CD : 10,6 Mo environ
Taux de compression : taille perdue / taille originale 9,6/10,6 = 0,91 (91 %).
Compression sans perte (FLAC…)
FLAC : Fast Lossless Audio Codec
Ce sont des algorithmes de compression qui ne détruisent pas d’information. Autrement dit, il est possible de récupérer l’intégralité des informations (et donc de la qualité du son) contenues dans le fichier non compressé.
Leur taux de compression est cependant bien moindre que celui des format de compression avec perte (20 à 40 %).
Tableau récapitulatif
| Compression | Avantages | Inconvénients |
|---|---|---|
| Non compressé |
Peu de puissance de calcul pour enregistrer/lire Éditable sans perte de qualité |
Taille très importante |
| Compression avec perte |
Très bon rapport qualité/taille Taux de compression paramétrable |
Perte de qualité par rapport à l’original Perte de qualité à chaque modification |
| Compression sans perte |
Meilleur rapport qualité/taille que non compressé Éditable sans perte de qualité |
Taille encore assez importante |