2.1 Deux siècles d’énergie électrique
L’énergie électrique accompagne chaque seconde de notre vie. Si nous devions nous en passer, ça nous ramènerait à la fin du XIXe siècle : éclairage au gaz ou à la bougie, chevaux, vélo ou train à vapeur pour se déplacer, et bien sûr ni ordinateur, ni téléphone, ni radio, ni télé…
L’électricité est produite à partir de nombreuses sources d’énergie différentes : combustible fossile, centrale hydroélectrique, centrale nucléaire, énergie solaire… Mais dans 92 % des cas, cette production fait intervenir un alternateur.
Le seul moyen de production d’énergie électrique qui ne soit pas anecdotique et qui ne fasse pas intervenir un alternateur est l’utilisation de panneaux photovoltaïques.


L’alternateur
- Reconnaître les éléments principaux d’un alternateur (source de champ magnétique et fil conducteur mobile) dans un schéma fourni.
- Analyser les propriétés d’un alternateur modèle étudié expérimentalement en classe.
- Définir le rendement d’un alternateur et citer un phénomène susceptible de l’influencer.
L’alternateur est à l’origine de plus 95% de l’électricité produite dans le monde. De fait, il s’agit donc d’un dispositif sur lequel repose entièrement nos sociétés industrialisées. Comment fonctionne-t-il ?
Un peu d’histoire
Michael Faraday, savant anglais (1791-1867), découvre l’induction électromagnétique en 1831. Ce phénomène est le suivant :
Je dis « il peut » car cela dépend de l’orientation du champ magnétique et du conducteur. Je n’en dirai pas plus ici.

C’est ce phénomène que l’on exploite dans les alternateurs.

Principe de fonctionnement d’un alternateur
Un alternateur génère du courant par induction électromagnétique. Le principe est toujours le même : une partie mobile, le rotor, tourne dans une partie fixe, le stator. Le rotor peut être un aimant permanent ou un électroaimant. Le stator est constitué d’un enroulement de fil de cuivre (appelé bobine). Ce dispositif produit un courant alternatif.
L’origine de l’énergie mécanique est très variable. Le rotor peut être mis en mouvement par une turbine entraînée par de la vapeur d’eau (centrale au charbon, au gaz, au pétrole, centrale nucléaire) ou de l’eau liquide (centrale hydroélectrique). Le rotor peut également être mis en mouvement par le vent (cas de l’hélice d’une éolienne) ou par un moteur (voiture, groupe électrogène).
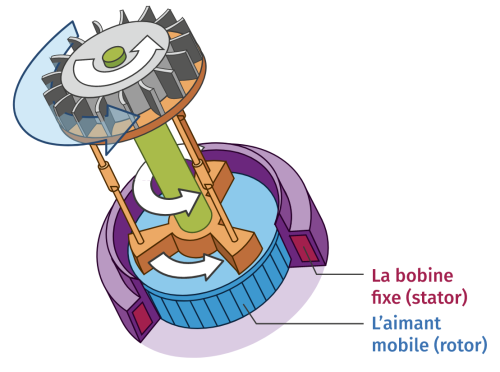

Importance de l’alternateur
1. Rechercher sur Internet les moyens de production d’énergie électrique ne faisant pas intervenir l’alternateur.
2. Rechercher qui est l’inventeur de l’alternateur.
Correction
1. Les panneaux solaires et les piles & batteries
2. Il s’agit de Nikola Tesla.
Rendement d’un alternateur
Le rendement d’un alternateur est la fraction d’énergie mécanique reçue qu’il est capable de convertir en énergie électrique.
Un rendement de 100 % signifie que l’alternateur convertit toute l’énergie mécanique reçue en énergie électrique. Cela est impossible en pratique. Les meilleurs alternateurs ont des rendements de l’ordre de 95 %.
Ce rendement est forcément inférieur à 1 (ou à 100 % si on parle en pourcentage), car, comme il y a des pièces en mouvement, il y a donc forcément des frottements qui font qu’une partie de l’énergie mécanique reçue est convertie en chaleur. De plus, la circulation d’un courant dans un conducteur ne se fait jamais sans résistance (sauf dans les supraconducteurs, mais malheureusement, on ne sait pas faire de matériau qui soit surpaconducteur à température ambiante). Il y a donc une partie de l’énergie électrique produite qui est perdue sous forme de chaleur par effet Joule.
Rendement d’un groupe électrogène
Voici ci-dessous les caractéristiques d’un groupe électrogène trouvées sur Internet.
Données techniques
Cylindrée : 125 cm³ essence (moteur 4 temps) ;
Puissance moteur max : 3 kW ;
Puissance électrique max : 2,7 kW ;
Ampérage max en 230 V : 11,7 A ;
Consommation : 400 g/kW/h

• Densité de l’essence : environ 0,75
✋ Il est important de vous souvenir des formules suivantes :
- Puissance (W) = Énergie (J) ÷ Durée (s)
- Puissance électrique = Tension (V) × Intensité (A)
- 1 kWh = 1000 W × 3600 s = 3,6 MJ
Ces formules sont normalement connues depuis de nombreuses années. 😉
1. L’« ampérage » (autre nom de l’intensité du courant électrique) annoncé est-il compatible avec la puissance électrique maximale annoncée ?
2. Quel est le rendement de l’alternateur de ce groupe électrogène ?
On se sert de ce groupe pour alimenter un appareil électrique consommant une puissance de 1,5 kW pendant 2 h.
3. Quel est le volume d’essence consommé ?
Au Gabon, le prix du kWh d’électricité acheté auprès de la SEEG est d’environ 100 FCFA. Le prix d’un litre d’essence est d’environ 595 FCFA.
4. Est-il plus économique de produire son électricité avec un groupe électrogène ou bien en l’achetant auprès de la SEEG ? Quel est l’intérêt d’un groupe électrogène ?
Correction
1. $*U×I*$ = 230×11,7 = 2691 W soit environ les 2,7 kW annoncés. C’est donc bien compatible.
2. L’alternateur reçoit 3 kW du moteur et fournit 2,7 kW. Rendement = 2,7/3 = 0,9 (90 %)
3. 400 g/kW/h × 1,5 kW × 2 h = 1200 g, soit 1200÷0,75 = 1600 mL = 1,6 L d’essence.
4. 3 kWh d’énergie électrique produite par le groupe électrogène consomme 1,6 L et donc coûte 950 FCFA environ. Ces mêmes 3 kW achetés à EPS coûtent 3×100 = 300 FCFA. C’est donc plus de 3 fois plus cher que l’électricité achetée auprès de la SEEG. L’intérêt d’un groupe électrogène et de pouvoir produire de l’électricité dans des endroits où le réseau électrique n’arrive pas, ou bien de compenser les défaillances du réseau.
Les panneaux photovoltaïques
- Comparer le spectre d’absorption d’un matériau semiconducteur et le spectre solaire pour décider si ce matériau est susceptible d’être utilisé pour fabriquer un capteur photovoltaïque.
- Tracer la caractéristique $*i(u)*$ d’une cellule photovoltaïque et exploiter cette représentation pour déterminer la résistance d’utilisation maximisant la puissance électrique délivrée.
Les semi-conducteurs
Les panneaux photovoltaïques, c’est-à-dire les panneaux solaires qui transforment une partie de l’énergie lumineuse reçue en énergie électrique, sont essentiellement constitués de silicium. Le silicium est un semi-conducteur.
Un semi-conducteur est un matériau dont la conductivité électrique est intermédiaire entre celle des métaux et celle des isolants.

Un matériau conducteur est constitué d’atomes dont les électrons périphériques peuvent passer librement de la bande de valence vers la bande de conduction car celles-ci se chevauchent. Ces matériaux conduisent donc le courant grâce à leurs électrons se trouvant dans la bande de conduction
Dans un matériau isolant, la différence d’énergie entre ces deux bandes (appelée gap) est trop importante : il est très difficile pour des électrons d’acquérir assez d’énergie pour passer dans la bande de conduction. Par conséquent, ces matériaux ne conduisent pas le courant.
Dans un matériau semi-conducteur, le gap est suffisamment faible pour qu’un apport d’énergie modeste, par des photons dans le domaine du visible ou de l’infrarouge par exemple, permette le passage des électrons de la bande de valence vers la bande de conduction. Le matériau passe ainsi d’un état isolant vers un état conducteur.
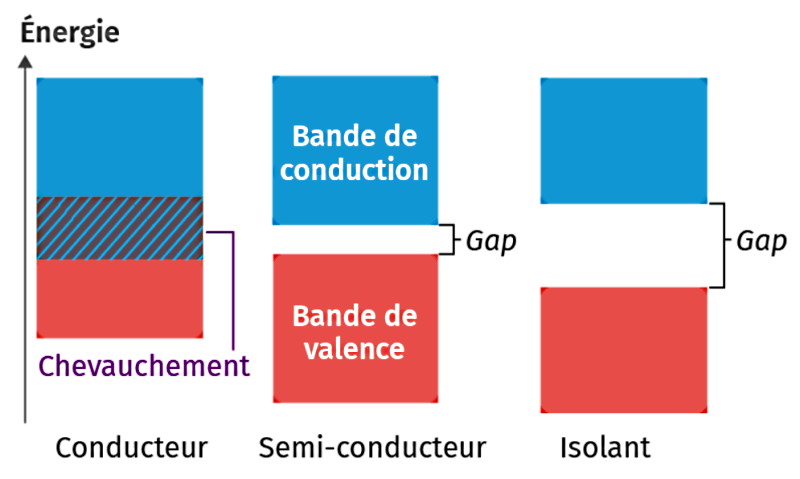
Le silicium est le matériau semi-conducteur le plus utilisé commercialement, du fait de ses bonnes propriétés, et de son abondance naturelle même s’il existe également des dizaines d’autres semi-conducteurs utilisés, comme le germanium ($*\ce{Ge}*$) ou l’arséniure de gallium ($*\ce{GaAs}*$).
Voici quelques valeurs de gap, c’est-à-dire d’énergie à fournir pour pouvoir faire passer un électron de la bande de valence à la bande de condution : 1,12 eV pour le silicium, 0,66 eV pour le germanium, 1,42 eV pour l’arséniure de gallium. On y reviendra dans un exercice un peu plus loin.
À l’échelle atomique, les énergies mises en jeu sont tellement faibles qu’on exprime souvent les valeurs en électron-volt (eV).
1 eV = 1,60·10-19 J
Énergie d’un photon
Un photon est un « grain » de lumière. Chaque photon transporte une certaine quantité d’énergie. Cette quantité d’énergie $*E*$ est reliée à la longueur d’onde $*\lambda*$ de la lumière associée au photon par la relation :
| $µ E = \frac {hc}\lambda µ$ | $*E*$ : énergie (J) $*h*$ : constante de Planck (6,63·10-34 J·s) $*c*$ : vitesse de la lumière (3,00·108 m·s-1) $*\lambda*$ : longueur d’onde (m) |
Énergie d’un photon
Le but de cet exercice est juste de vous faire utiliser un peu la formule $*E = \frac {hc} \lambda*$, en prenant garde au problème des unités. On se resservira de cette formule dans des cas plus concrets dans la suite du chapitre.
1. Quelle est l’énergie d’un photon associé à une lumière rouge de longueur d’onde $*\lambda*$ = 650 nm ? Exprimer le résultat en eV.
2. Proposer une formule permettant de passer directement d’une longueur d’onde en nm à une énergie en eV. Elle nous sera très utile par la suite… 😊
Correction
1. $*E = \dfrac {hc}\lambda = \dfrac {6,63·10^{-34}×3·10^8}{650·10^{-9}} = *$ 3,06·10-9 J, soit 1,91 eV.
2. Il faut trouver la valeur de $*a*$ dans la relation $*E = \dfrac a\lambda*$, avec $*\lambda*$ en nm et $*E*$ en eV.
Pour cela, il suffit de prendre les deux valeurs de à la question précédente (650 nm et 1,9125 eV) et calculer $*a*$ :
$*a*$ = 650×1,9125 = 1243 nm·eV.
Le spectre solaire
Le soleil émet de la lumière… Ça, vous le saviez déjà. 😎
Mais il n’émet pas que de la lumière visible. Il émet également des rayonnements ultraviolets et infrarouges. Et il n’émet pas toutes les longueurs d’onde en quantité égale. De plus, les molécules de l’atmosphère absorbent une partie de la lumière solaire, comme le montre le graphique ci-dessous.
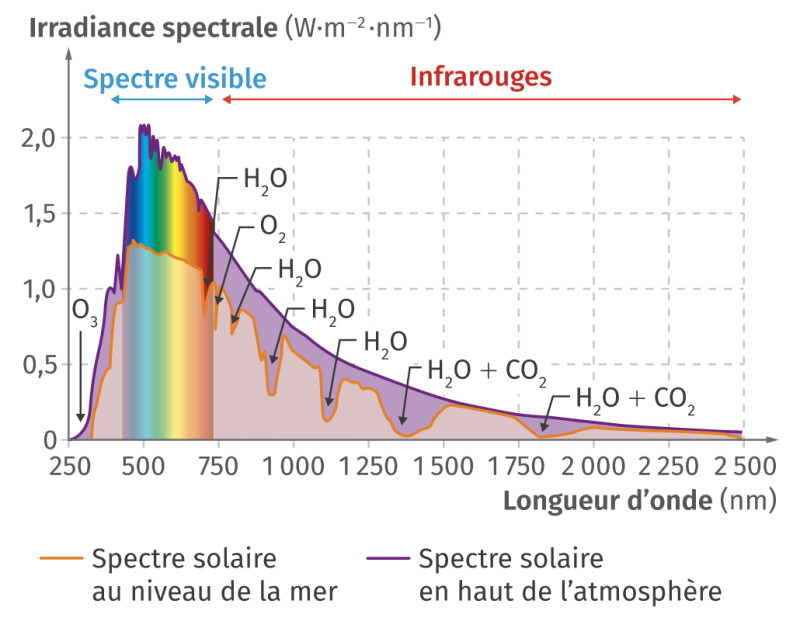
Semi-conducteurs et lumière solaire
Lorsqu’un semi-conducteur absorbe un photon dont l’énergie est supérieure ou égale à son gap, un électron passe alors dans la bande de conduction. C’est ce principe qui est utilisé dans les panneaux photovoltaïques, nous y reviendrons plus tard.
Donner la partie du spectre solaire absorbée par :
1. le silicium (gap de 1,12 eV)
2. le germanium (gap de 0,66 eV)
3. l’arséniure de gallium (gap de 1,42 eV)
Correction
Silicium gap de 1,12 eV, donc $*\lambda*$ = 1,11 µm. Domaine du spectre utilisé : des ultraviolets jusqu’aux infrarouges à 1,11 µm.
Germanium : gap de 0,66 eV, donc $*\lambda*$ = 1,88 µm. Domaine du spectre utilisé : des ultraviolets jusqu’aux infrarouges à 1,88 µm.
Arséniure de gallium : gap de 1,42 eV, donc $*\lambda*$ = 875 nm. Domaine du spectre utilisé : des ultraviolets jusqu’aux infrarouges proches à 875 nm.
Principe de fonctionnement des panneaux photovoltaïques

Lorsqu’un semi-conducteur absorbe un photon d’énergie supérieure à celle de son gap, l’énergie excédentaire est transformée en chaleur. Par exemple, si un panneau solaire à base de silicum (gap de 1,1 eV) absorbe un photon d’énergie 3 eV, seul 1,1 eV est converti en énergie électrique. Le reste (3 - 1,1 = 1,9 eV) est perdu sous forme de chaleur. Les photons dont l’énergie est inférieure au gap ne sont pas absorbés et donc pas convertis en énergie électrique.
Cela explique le faible rendement des panneaux solaires au silicium (de l’ordre de 10-15 % pour des panneaux « moyens », jusqu’à 20-25 % pour les meilleurs – et donc les plus chers).
De très nombreuses pistes sont actuellement l’objet de recherche. Je vous en cite quelques-unes :
- Les panneaux à cellules multi-jonctions : ils sont constitués de différentes couches de semi-conducteurs, chacune particulièrement efficace dans un domaine précis du spectre du Soleil. Ces panneaux coûtent beaucoup plus chers que les panneaux « classiques » car leur fabrication est complexe. Ils ont cependant des rendements plus élevés, de l’ordre de 30 %. Ils sont utilisés dans le spatial.
- Les panneaux à cellules organiques : le matériau semi-conducteur est fabriqué avec des molécules organiques. Ils ne nécessitent pas de ressources rares et ne coûte pas cher à fabriquer, mais leur rendement est faible (de l’ordre de 5-7 %) et les cellules se dégradent assez vite au contact de l’humidité et de l’oxygène de l’air.
Activité : Caractéristique d’une cellule photovoltaïque
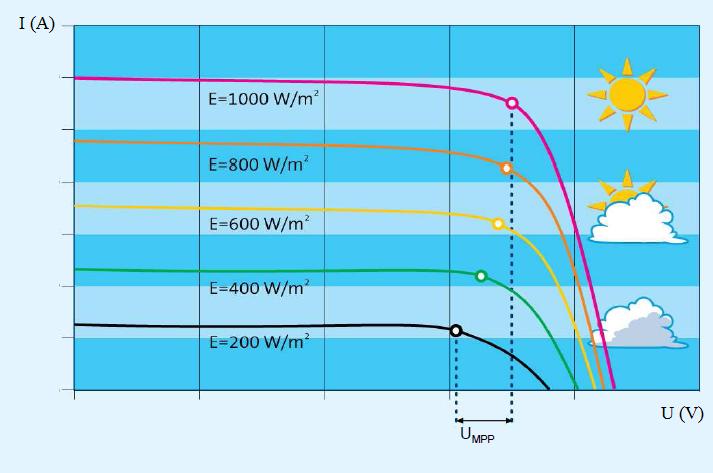
La puissance électrique d’une cellule photovoltaïque dépend de nombreux facteurs : la quantité de lumière qu’elle reçoit, le profil spectral de cette lumière, sa température, mais elle dépend aussi de l’intensité du courant électrique qui circule dans le dispositif qui est raccordé à ses bornes.
Cette activité vous propose d’étudier ce dernier facteur, très important. En effet, lorsqu’on dispose d’une installation de panneaux solaires, il est important d’optimiser son fonctionnement pour récupérer un maximum d’énergie.
Pour cette étude, on a mesuré l’intensité $*I*$ du courant électrique délivrée par une cellule photoélectrique ainsi que la tension $*U*$ correspondante à ses bornes, en faisant varier la résistance électrique du circuit branché sur la cellule.
Données : surface de la cellule 100 cm2 ; puissance lumineuse surfacique reçue : 1000 W·m-2 ; température de fonctionnement : 25 °C.
Les valeurs mesurées sont consignées dans ce fichier Excel.
Travail demandé
• Afficher le graphique $*I=f(U)*$ pour cette cellule.
• Créer la grandeur puissance $*P=UI*$, puis afficher le graphique $*P=f(U)*$.
Questions
1. Déterminer les valeurs de tension $*U_{P_{max}}*$ et d’intensité $*I_{P_{max}}*$ pour lesquelles la puissance délivrée par cette cellule est maximale.
2. Quelle est la valeur de la résistance à brancher sur la cellule si on veut qu’elle fonctionnement à son point de fonctionnement optimum ? (rappelez-vous la loi d’Ohm : $*U=RI*$)
3. Calculer la puissance lumineuse reçue par la cellule, puis en déduire son rendement lorsqu’elle fonctionne à son point de fonctionnement optimum.
Une cellule n’est capable que de fournir une tension très faible. Dans les panneaux solaires, elles sont associées en série afin de pouvoir fournir une tension plus élevée. En série, les tensions de chaque cellules s’ajoutent, mais l’intensité reste identique à celle d’une seule cellule.
Un apprenti bricoleur souhaite utiliser son ordinateur directement sur un panneau solaire. L’ordinateur fonctionne sous une tension de 19 V en utilisant un courant de 0,7 A. Cette personne décide donc d’associer des cellules en série de manière à avoir une tension « à vide » (c’est-à-dire lorsque le dispositif ne fournit aucun courant) de 19 V.
4. Combien de cellules cette personne doit associer pour avoir la tension voulue ?
5. Afficher le graphique $*U’=f(I)*$ pour cette association de cellules en série.
Comment évolue la tension aux bornes du panneau solaire lorsqu’il branchera son ordinateur ?
6. Arrivera-t-il à utiliser l’ordinateur au point de fonctionnement optimal des panneau ?
Ces dernières questions ont pour objectif de vous faire réaliser qu’un dispositif de régulation ainsi qu’un système de batteries adapté sont nécessaires pour pouvoir utiliser des panneaux solaires de manière optimale.
Caractéristique d’une cellule photovoltaïque
Une cellule photovoltaïque présente un point ($*U*$, $*I*$) de fonctionnement optimal, pour lequel son rendement est le plus élevé possible.
Pour être efficace, une installation solaire doit toujours fonctionner proche du point de fonctionnement optimal de ses panneaux photovoltaïques. Ceci est rendu possible en ajoutant un régulateur de charge qui contrôle le courant et la tension à la sortie des panneaux pour optimiser la puissance maximale en sortie. On appelle cet appareil un régulateur MPPT (Maximum Power Point Tracker). Cet appareil doit être couplé à des batteries, dont il gère la charge et la décharge.
Cellule photovoltaïque transparente
De nombreuses recherches sont menées pour développer des cellules photoélectriques transparentes. Pour être transparentes, ces cellules ne doivent pas absorber la lumière visible (entre 400 et 800 nm).
1. Calculer la valeur du gap d’un matériau semi-conducteur qui n’absorbe que les ultraviolets.
2. Une cellule semi-transparente de 8,0 cm × 12,5 cm est capable de produire 0,72 W lorsqu’elle reçoit un éclairage de 1000 W·m-2. Calculer son rendement et le comparer au rendement des cellules conventionnelles.
3. Quel peut être l’intérêt de ces cellules ?
Correction
1. Pour les UV, $*\lambda*$ ≤ 400 nm. Donc le gap doit être supérieur ou égal à 3,1 eV.
2. Il faut d’abord calculer la surface de la cellule : $*S*$ = 0,08×0,125 = 0,010 m2. Donc la cellule reçoit 10 W. Ce qui fait un rendement de 0,72÷10 = 0,072 soit 7,2 %. C’est relativement faible par rapport aux cellules conventionnelles (environ 15 %).
3. Si elles sont transparentes, elles peuvent être déposées sur des vitres.
Caractéristiques d’une cellule photovoltaïque
On se propose d’étudier le fonctionnement d’une cellule photovoltaïque. Grâce aux mesures réalisées aux bornes de la cellule, on trace la caractéristique tension - intensité (en trait plein) et la caractéristique tension - puissance (en pointillé).
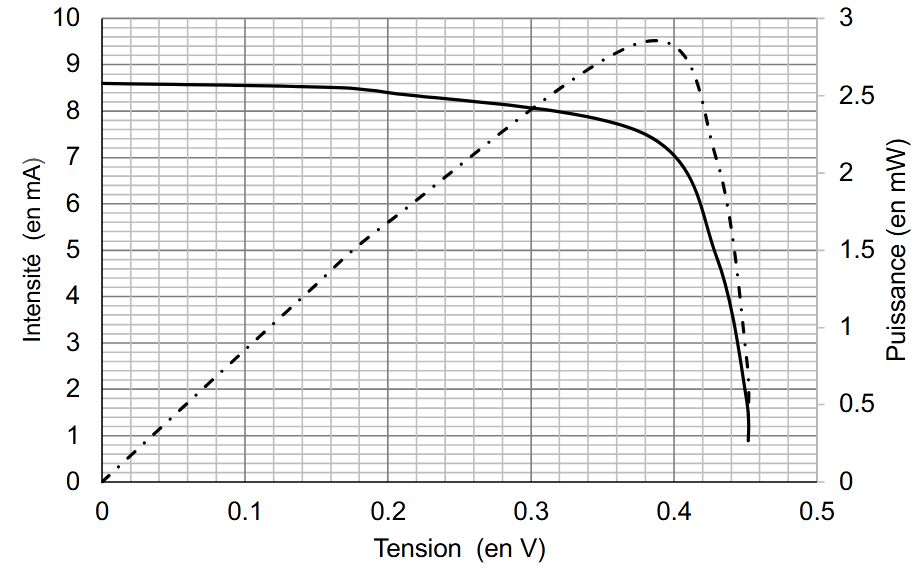
1. Déterminer graphiquement la valeur de la puissance maximale $*P_{max}*$.
2. En déduire la valeur de l’intensité maximale $*I_{max}*$ et celle de la tension maximale $*U_{max}*$ lorsque la cellue fournit sa puissance maximale.
3. En déduire que la valeur de la résistance du récepteur à utiliser avec le panneau pour un fonctionnement optimal est environ égale à 50 Ω.
Correction
1. $*P_{max}*$ ~ 2,9 mW
2. Par lecture graphique, $*U_{max}*$ ~ 0,395 V et $*I_{max}*$ ~ 7,5 mA
3. $*R=U÷I*$ = 0,395÷7,5·10-3 ~ 50 Ω
Révision & entraînement
Alternateur de voiture
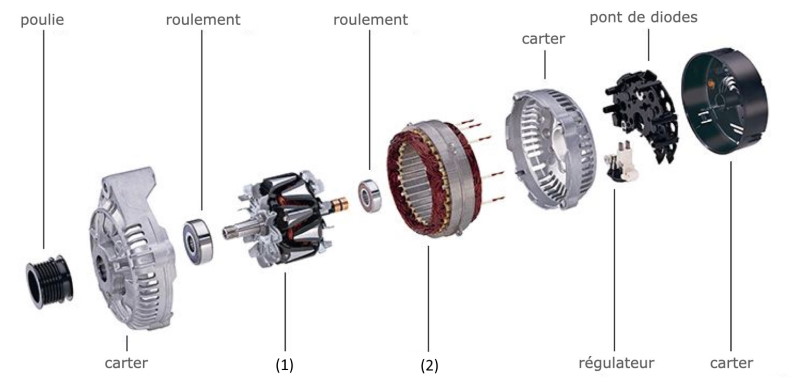
Un alternateur est un dispositif qui convertit l’énergie mécanique en énergie électrique. La figure ci-dessous montre la constitution d’un alternateur de voiture.
1.a. Quelle est la source de l’énergie mécanique fournie à l’alternateur dans le cas d’une voiture ?
1.b. Pourquoi est-il nécessaire d’avoir un alternateur sur une voiture ?
1.c. Citer deux autres « objets » utilisant un alternateur.
2.a. Donner le nom de la pièce n°1, en remarquant qu’elle est mobile. De quoi est-elle constituée ?
2.b. Donner le nom de la pièce n°2 (celle-ci est fixe). De quoi est-elle constituée ?
Le rendement d’un alternateur de voiture est de l’ordre de 50 %. La transmission de l’énergie mécanique du moteur vers l’alternateur se fait pas une courroie et le rendement de cette transmission par courroie est de l’ordre de 90 %.
3. Définir le rendement de l’alternateur.
Une voiture circule avec son système d’éclairage allumé. On considère que la puissance électrique consommée par la voiture dans ces conditions vaut 200 W. Cette puissance est délivrée uniquement par l’alternateur (en conditions normales, la batterie n’est pas utilisée).
4. Calculer la puissance mécanique fournie à l’alternateur par la courroie, puis la puissance mécanique fournie par le moteur à l’ensemble {courroie + alternateur} dans ces conditions.
5. Calculer l’énergie produite par l’alternateur dans ces conditions pendant 30 minutes. Exprimer le résultat en W·h.
Correction
1.a. Il s’agit du moteur
1.b. La voiture a besoin d’énergie électrique (éclairage, électronique du moteur, équipement de l’habitacle). La batterie fournit cette énergie lorsque le moteur ne fonctionne pas, mais il faut pouvoir la recharger. C’est le rôle de l’alternateur.
1.c. Parmi les « objets » que l’on peut coter, il y a les centrales thermiques, les centrales nucléaires, les éoliennes, les centrales hydroélectriques…
2.a. Il s’agit du rotor, constitué d’un aimant.
2.b. Il s’agit du stator, constitué de bobine de fil de cuivre.
3. C’est le rapport entre l’énergie électrique produite et l’énergie mécanique reçue.
4. Le puissance mécanique reçue par l’alternateur est de 200÷0,5 = 400 W. Le moteur doit fournir une énergie un peu plus grande car la courroie n’a un rendement que de 90 %. Il doit fournir 400÷0,9 = 444 W.
Solar Impulse
L’avion Solar Impulse 2 est le premier avion entièrement solaire à avoir réaliser le tour du monde entre mars 2015 et juillet 2016.

Données
- Surface des cellules : $*S*$ = 270 m2
- Rendement des cellules de l’avion : 23,0 %
- Gap du silicium : 1,12 eV
- L’avion dispose de 4 moteurs électriques d’une puissance maximale totale de 51,5 kW.
- L’avion dispose de batteries pouvant stocker 154 kWh.
- Le jour, l’avion est soumis à une puissance solaire surfacique moyenne de 1,00 kW·m-2 pendant 10 h par jour.
- Constante de Planck : $*h*$ = 6,63·10-34 J·s
- Vitesse de la lumière : $*c*$ = 3,00·108 m·s-1
- Valeur de l’électron-volt : 1 eV = 1,60·10-19 J
1. Calculer la longueur d’onde maximale d’un photon susceptible d’être absorbé par le silicium. À quel domaine du spectre électromagnétique ce rayonnement appartient-il ?
2. Un photon d’énergie 1,85 eV est absorbé par une cellule photovoltaïque. Donner l’énergie électrique produite grâce à ce photon (vous pouvez garder le résultat en électron-volt).
3. Montrer que, de jour, les panneaux solaires de l’avion fournissent une puissance électrique de 62,1 kW.
4. En moyenne, un quart de la puissance électrique produite pendant la journée sert à recharger les batteries. Cette puissance suffit-elle à recharger entièrement les batteries de l’avion ?
5. Si on considère que l’avion ne reçoit aucune énergie solaire pendant 8 h par jour, à quelle pourcentage de la puissance maximale le pilote doit-il faire fonctionner les moteurs s’il ne veut pas utiliser plus que 80 % des capacités de stockage des batteries durant ces 8 h ?
Correction
1. Pour pouvoir utiliser la relation $* E = \dfrac {hc}\lambda *$, il faut d’abord convertir l’énergie en joule.
$*E*$ = 1,12 eV = 1,79·10-19 J.
On calcule ensuite $*\lambda *$ :
$µ \lambda = \frac {hc}E = \frac {6,63·10^{-34}×3·10^8}{1,79·10^{-19}} µ$
On trouve $*\lambda*$ = 1,11·10-6 m soit 1110 nm environ. Cette longueur d’onde est dans le domaine des infrarouges.
2. L’énergie produite est de 1,12 eV (l’énergie supérieure au gap est perdue).
3. Chaque m2 de l’avion reçoit une puissance lumineuse de 1,00 kW. Il y a 270 m2 de panneaux solaires, donc ces panneaux reçoivent une puissance lumineuse de 270 kW. 23 % de cette énergie est convertie en électricité, soit une puissance de 270×0,23 = 62,1 kW.
4. La puissance servant à recharger les batteries est de 62,1×0,25 = 15,5 kW. Cette puissance est produite pendant 10 h, donc cela représente une énergie de 15,5 kW × 10 h = 155 kWh. Cette énergie correspond à ce que les batteries peuvent stocker (154 kW) donc elles peuvent être entièrement rechargées pendant la journée.
5. Pendant ces 8 h de nuit, le pilote dispose d’une énergie de 154×0,8 = 123 kWh. Cette énergie doit pouvoir durer 8 h, cela correspond donc à une puissance de 123÷8 = 15,4 kW.
Les moteurs ne doivent pas être utilisés à une puissance supérieure à 15,4 kW, ce qui représente 15,4÷51,5 = 0,30 (soit 30 % de leur puissance maximale).