3.2 Réseaux sociaux & graphes
L’étude des relations entre utilisateurs des réseaux sociaux peut fournir beaucoup d’information aussi bien aux gérants de ces réseaux sociaux qu’aux sociologues voire aux services secrets. Pour mener ces études, il est nécessaire de modéliser mathématiquement ces relations. On utilise pour cela des « graphes ».
Le « petit monde »
L’expérience de Milgran
1. Après avoir regardé la vidéo ci-dessus, expliquez la notion de « petit monde ».
2. Expliquez pourquoi cette expérience a souvent été critiquée
Les graphes
- Déterminer le rayon, le diamètre et le centre d’un graphe simple.
Imaginez un réseau social ayant 6 abonnés (A, B, C, D, E et F) où :
- A est ami avec B, C, D et E
- B est ami avec A et D
- C est ami avec A, E et D
- D est ami avec tous les autres abonnés
- E est ami avec A, C, D et F
- F est ami avec E et D
On peut représenter visuellement ce réseau social par un graphe. Chaque abonné est un sommet du graphe et chaque relation « X et Y sont amis » par un trait reliant X et Y, qu’on appelle une arête ou un lien.
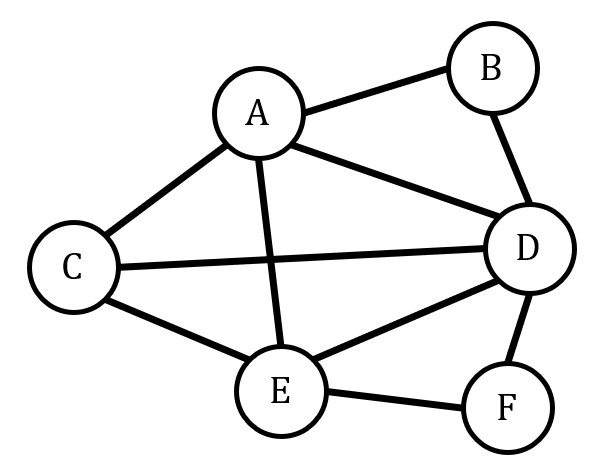
Les graphes sont des objets mathématiques très utilisés, notamment en informatique. En effet, l’analyse d’un réseau social comptant de milliers, voires des millions d’abonnés, ne peut pas se faire « à la main ». Elle doit être faite par ordinateur.
Quelques définitions
Chaîne : une suite de sommets directement reliés entre eux.
Exemple : A-D-C-E est une chaîne reliant A à E.
Degré/valence d’un sommet : nombre de liens reliant ce sommet.
Distance entre 2 sommets : nombre minimum d’arêtes d’une chaîne allant d’un sommet à l’autre.
Exemple : la distance entre A et E est de 1, la distance entre A et F est de 2.
Excentricité d’un sommet : distance maximale entre ce sommet et n’importe quel autre sommet du graphe.
Exemple : l’excentricité de A vaut 2 – car pour atteindre n’importe quel sommet à partir de A, on a au plus une distance de 2 à parcourir.
Centre : sommet(s) d’excentricité minimale (le centre n’est pas nécessairement unique).
Dans le cas de notre graphe, tous les sommets ont une excentricité de 2, sauf D qui a une excentricité de 1. D est donc le sommet du graphe.
Rayon : valeur de l’excentricité minimale.
Ici, le centre du graphe, c’est D qui a une excentricité de 1. Donc le rayon du graphe vaut 1.
Diamètre : valeur de l’excentricité maximale.
Dans notre graphe, tous les sommets ont une excentricité d’au plus 2, donc le diamètre du graphe est 2.
Caractéristiques d’un graphe
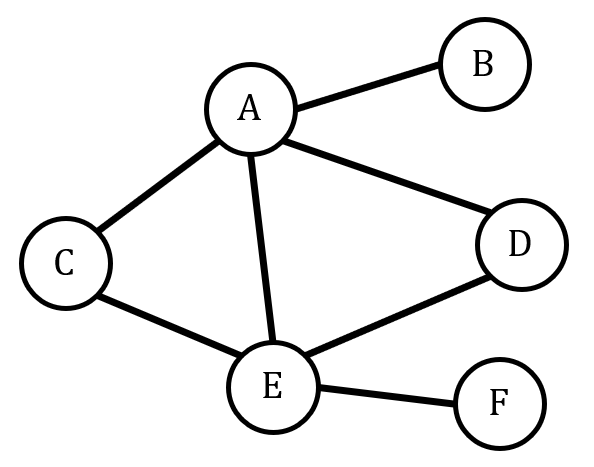
1. Donner l’excentricité de chaque sommet du graphe ci-dessus.
2. Donner le ou les centre(s) de ce graphe, ainsi que son rayon et son diamètre.
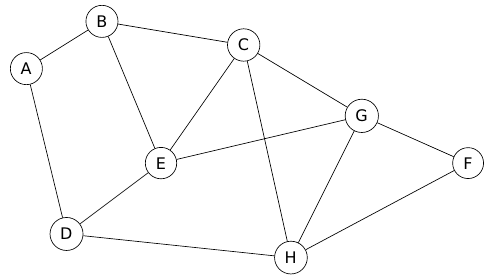
3. Mêmes questions pour le graphe ci-dessus.

4. Mêmes questions pour le graphe ci-dessus. Non, je plaisante 😊