C2. Concentration et dosage spectrophotométrique
Réaliser un dosage, c’est déterminer la concentration d’un soluté présent dans une solution. Nous allons voir dans ce chapitre une technique particulière de dosage qui fait appelle à la mesure de l’absorbance d’une solution colorée.
Concentration d’une solution
- Déterminer la quantité de matière d’un soluté à partir de sa concentration en masse ou en quantité de matière et du volume de solution.
Rien de nouveau dans ce paragraphe. Vous savez tout depuis la 2nde, c’est pourquoi je vais aller un peu vite. 😊
Une solution, c’est un liquide (appelé solvant) dans lequel sont dissous un ou plusieurs solutés. C’est le cas de la très grande majorité des liquides qui nous entourent. En fait, les liquides purs sont très rares dans notre environnement quotidien. La plupart du temps, il s’agit de solutions.
Concentration molaire : c’est la qdm de soluté par unité de volume de solution (généralement par litre). Unité usuelle : mol·L-1.
Concentration massique : c’est la masse de soluté par unité de volume de solution (généralement par litre). Unité usuelle : g·L-1.
Les deux formules suivantes sont à retenir absolument :
| $µ c = \frac nV µ$ | $*c*$ : concentration molaire $*n*$ : qdm $*V*$ : volume de la solution |
| $µ c_m = \frac mV µ$ | $*c_m*$ : concentration massique $*m*$ : masse $*V*$ : volume de la solution |
Vous devez également savoir préparer une solution par dissolution du soluté dans le solvant et par dilution d’une solution mère. Voir Techniques de TP pour le protocole. On ne va pas faire un TP tout de suite là-dessus, mais voir l’exercice « expérimental » ci-dessous. On aura de toute façon l’occasion de préparer des solutions un peu plus tard dans l’année.
Concentration de solutions
1. Quelle qdm de chlorure de sodium ($*\ce{Na+(aq) + Cl–(aq)}*$) contiennent 200 mL d’une solution de concentration $*c*$ = 0,15 mol·L-1 ? Réaliser expérimentalement 50 mL de cette solution.
2. De quelle masse de chlorure de sodium a-t-on besoin pour réaliser 100 mL de solution à 0,90 g·L-1. Quel problème va se poser si l’on souhaite réaliser cette solution en s’aidant d’une balance précise au 100e de gramme ? Comment peut-on le contourner ?
3. Un biologiste souhaite préparer 500 mL d’une solution de glucose ($* \ce{C6H12O6}*$) à 20 mmol·L-1. De quelle masse de glucose a-t-il besoin ?
4. Déterminer la masse de chlorure de lithium ($* \ce{LiCl}*$) nécessaire pour réaliser 650 mL de solution de concentration 87,2 mmol/L.
5. On dispose d’une solution mère de concentration $*c_0*$ = 0,10 mol·L-1. On souhaite réaliser 250 mL d’une concentration fille $*c_F*$ = 4,0 mmol·L-1. Donner le protocole pour réaliser cette dilution.
Correction
1. $*n = cV =*$ 0,15×0,200 = 0,030 mol.
Pour préparer cette solution, il faut une qdm $*n = cV = *$ 0,15×0,05 = 7,5·10-3 mol.
Et donc peser une masse $*m = nM = *$ 7,5·10-3×58,5 = 0,44 g.
Voir Techniques de TP pour le protocole à connaître par cœur.
2. On a besoin d’une masse $*m = c_mV = *$ 0,90×0,1 = 0,09 g.
La mesure ne sera pas précise. En effet, que la masse pesée soit 0,085 g ou 0,0949 g, la balance arrondit à 0,09 g. Il faut donc préparer un volume plus important de solution (1 L) puis en prélever 100 mL.
3. Masse molaire du glucose $*M*$ = 180 g·mol-1. Qdm nécessaire $*n = cV = *$ 0,020×0,5 = 0,010 mol. Masse nécessaire $*m = nM *$ = 0,010×180 = 1,80 g.
4. Masse molaire du chlorure de lithium $*M*$ = 42,4 g·mol-1. QdM nécessaire $*n = cV =*$ 0,0872×0,65 = 0,0567 mmol. Masse nécessaire $*m = nM=*$ 0,0567×42,4 = 2,40 g
5. On calcule le volume de solution mère à utiliser : $µ V_M = \frac {C_FV_F}{C_M} = \frac {0,004×250}{0,10} = 10 \; \mathrm{mL} µ$
Protocole
• Prélever 10 mL de solution mère avec une pipette jaugée.
• Verser ces 10 mL dans une fiole jaugée de 250 mL.
• Compléter avec de l’eau distillée jusqu’au trait de jauge.
• Boucher, agiter.
Couleurs et spectre d’absorption
- Expliquer ou prévoir la couleur d’une espèce en solution à partir de son spectre UV-visible.
Spectre de la lumière blanche
La lumière blanche est composée d’un ensemble de radiations de toutes les couleurs, c’est-à-dire de toutes les longueurs d’onde comprises entre 400 et 800 nm. La principale source de lumière blanche dans notre entourage, c’est le Soleil.
Un spectre lumineux, c’est ce qu’on obtient après avoir décomposé une lumière en l’ensemble des radiations qui la constitue.
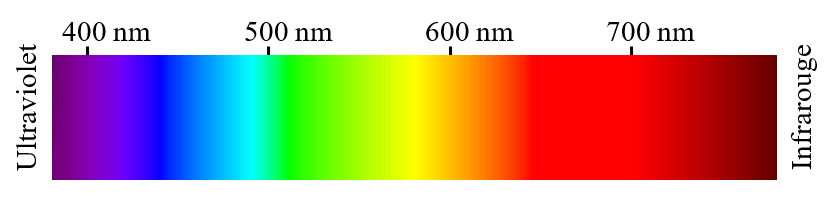
Couleur d’une solution
Lorsque de la lumière blanche traverse une solution colorée, certaines radiations (c’est-à-dire certaines couleurs) sont absorbées.
La couleur visible de la solution est la couleur complémentaire des radiations absorbées. Le cercle chromatique permet de trouver quelle est la couleur complémentaire d’une couleur donnée.
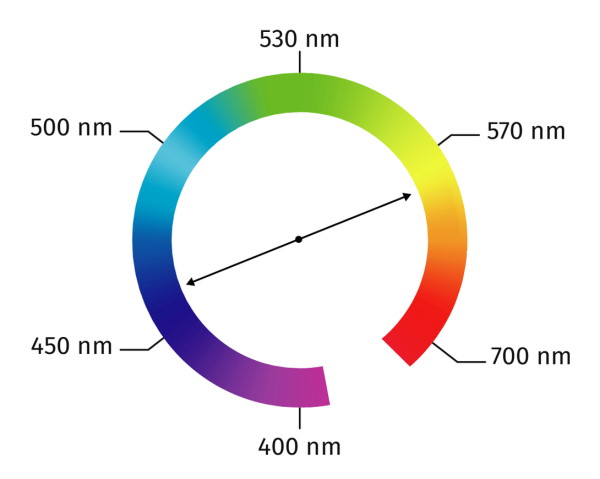
Par exemple, une solution jaune absorbe principalement les radiations qui ont une longueur d’onde proche du bleu.
Spectre d’absorption
Le spectre d’absorption d’une solution, c’est le graphique qui montre l’absorbance $*A*$ de la solution en fonction de la longueur d’onde de la lumière qui la traverse.
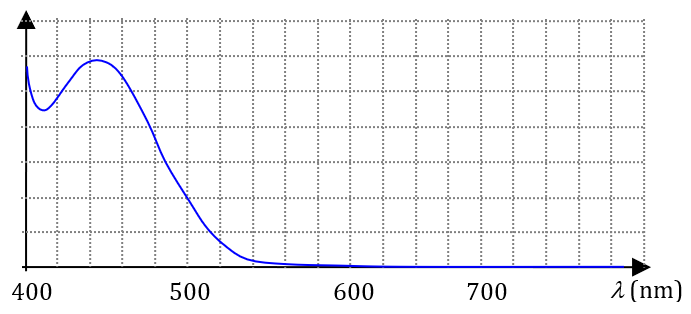
L’absorbance est liée à la quantité de lumière absorbée, à une longueur d’onde donnée. Par exemple, le diiode $*\ce{I2}*$, de couleur rouge-orangé en solution aqueuse, absorbe principalement dans le bleu et le vert, comme le montre le spectre d’absorption ci-dessous.
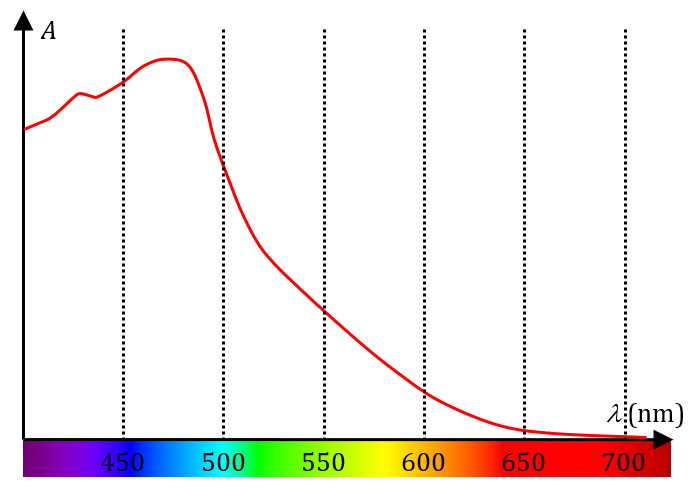
Couleurs d’une solution
1. Justifier la couleur bleue du bleu de méthylène à partir de son spectre d’absorption ci-dessous.
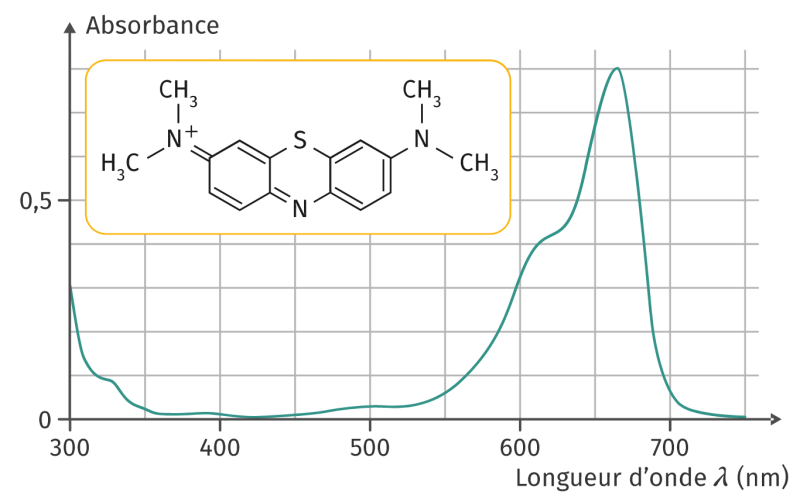
2. Même question pour une solution contenant des ions permanganate ($*\ce{MnO4–}*$) de couleur violette.
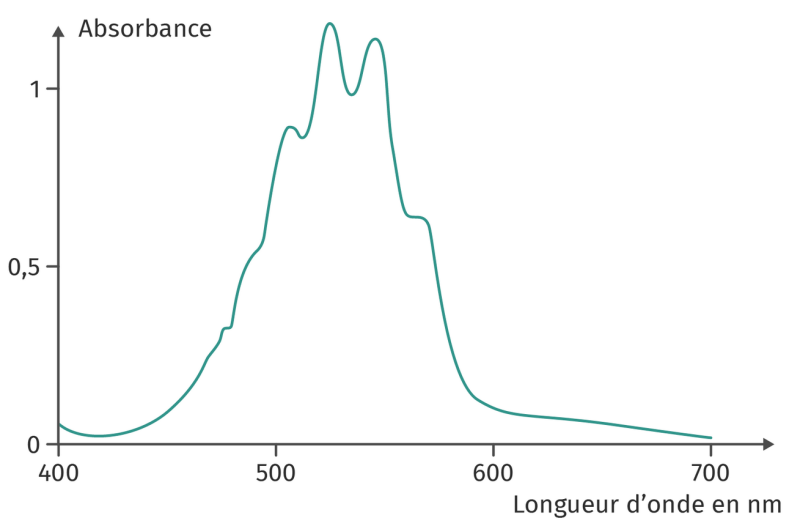
Correction
1. Absorption forte entre 630 et 680 nm, c’est-à-dire rouge-orange. Couleur complémentaire : bleue
2. Absorption forte entre 500 et 570 nm, c’est-à-dire verte. Couleur complémentaire : violette
Dosage spectrophotométrique
- Déterminer la concentration d’un soluté à partir de données expérimentales relatives à l’absorbance de solutions de concentrations connues.
Explication de quelques termes
• L’absorbance $*A*$ d’une solution, pour une longueur d’onde donnée, est liée à la quantité de lumière absorbée par la solution dans cette longueur d’onde. Une absorbance nulle signifie que la solution n’absorbe pas du tout la lumière à cette longueur d’onde.
• Un spectrophotomètre (ou colorimètre) est un appareil permettant de mesurer l’absorbance d’une solution à une concentration donnée.
• Doser, c’est déterminer la concentration (massique ou molaire) d’une solution.
TP Dosage spectrophotométrique
- Proposer et mettre en œuvre un protocole pour réaliser une gamme étalon et déterminer la concentration d’une espèce colorée en solution par des mesures d’absorbance. Tester les limites d’utilisation du protocole.
Objectif : trouver la relation qui lie l’absorbance $*A*$ d’une solution à sa concentration $*c*$.
Matériel disponible
- Une solution aqueuse S0 de bleu patenté, $*c*$ = 24,0 mmol·L-1 ;
- Deux burettes graduées ;
- Une solution de bleu patenté de concentration inconnue ;
- Un colorimètre.
Élaboration d’une stratégie de recherche
Comment trouver la loi mathématique reliant l’absorbance $*A*$ d’une solution (pour une longueur d’onde donnée) à sa concentration $*c*$ en espèce colorée ?
Réalisation d’une échelle de solutions étalons
À partir de la solution-mère S0, préparer 24 mL de 8 solutions-filles (voir les concentrations dans le tableau ci-dessous).
Pour aller plus vite : réaliser vos dilutions avec deux burettes graduées, une contenant de l’eau distillée et l’autre contenant la solution-mère.
Le travail sera réparti entre les binômes.
| $*c*$ (mmol·L-1) | $*V_{S_0}*$ (mL) | $*V_{\mathrm{eau}}*$ (mL) | |
|---|---|---|---|
| S1 | 21 | ||
| S2 | 18 | ||
| S3 | 16 | ||
| S4 | 14 | ||
| S5 | 12 | ||
| S6 | 9 | ||
| S7 | 6 | ||
| S8 | 3 |
Réalisation du graphique A = f (c)
Faire un blanc à la longueur d’onde appropriée pour la solution de bleu patenté.
Réaliser les 9 mesures d’absorbance (de S0 à S8) et tracer le graphique $*A = f (c)*$ avec Excel.
Exploitation
1. Comment peut-on, grâce à ce graphique, déterminer la concentration d’une solution de bleu patenté de concentration inconnue ?
2. Que faire si cette solution est trop concentrée ?
Loi de Beer-Lambert
Cette loi dit que, pour des solutions suffisamment diluées (c’est-à-dire dont l’absorbance n’est pas trop forte), l’absorbance $*A*$ d’une espèce chimique en solution est proportionnelle à la concentration de cette espèce. Ceci se traduit par la relation :
| $*A = k·c*$ | $*A*$ : absorbance (pas d’unité) $*c*$ : concentration $*k*$ : constante de proportionnalité |
Eh bien ça dépend de la qualité du spectrophotomètre qu’on utilise… 😊 Les nôtres ne sont même pas des vrais spectrophotomètres, mais des colorimètres, c’est-à-dire, pour simplifier, des spectrophotomètres très basiques. Si l’absorbance est supérieur à 1, leur mesure n’est pas très fiable.
La constante de proportionnalité $*k*$ dépend, entre autres paramètres, de la longueur d’onde à laquelle est mesurée l’absorbance, de l’espèce chimique qui absorbe la lumière, de l’épaisseur de l’échantillon traversé par la lumière, etc. Cette constante est généralement déterminée expérimentalement.
Elle peut être exprimée sous la forme $*k = \epsilon_\lambda·l*$ où :
- $*\epsilon_\lambda*$ est le coefficient d’extinction molaire. Il dépend de l’espèce chimique considérée et de la longueur d’onde utilisée.
- $*l*$ est l’épaisseur de solution traversée.
Protocole d’un dosage spectrophotométrique
Un dosage est une méthode permettant de déterminer la concentration d’une espèce en solution.
Comme vous serez amené, d’ici au bac, à réaliser plusieurs fois des dosage spectrophotométrique, je le mets dans la partie Techniques de TP.
Dosage de l’ion dichromate
Pour doser par spectrophotométrie une solution jaune de dichromate de potassium ($*\ce{2K+(aq) + Cr2O7^2–(aq)}*$), on a préparé 5 solutions de concentration $*c*$ différentes. La mesure de leur absorbance $*A*$, pour une longueur d’onde de 400 nm (couleur bleue), a donné les résultats suivants :
| $*c*$ (mmol·L-1) | 5,0 | 4,0 | 3,0 | 2,0 | 1,0 |
|---|---|---|---|---|---|
| Absorbance | 1,48 | 1,24 | 0,90 | 0,59 | 0,31 |
1. Justifier la valeur de la longueur d’onde choisie.
2. Tracer la courbe d’étalonnage $*A = f (c)*$. La loi de Beer-Lambert est-elle vérifiée ?
3. Une solution de concentration $*c'*$ inconnue a, dans les mêmes conditions de mesure, une absorbance $*A'*$ = 1,12. En déduire la valeur de $*c'*$.
Correction
1. À 400 nm, l’absorbance est forte (mais on aurait pu aussi bien choisir 450 nm).
2. Graphique :
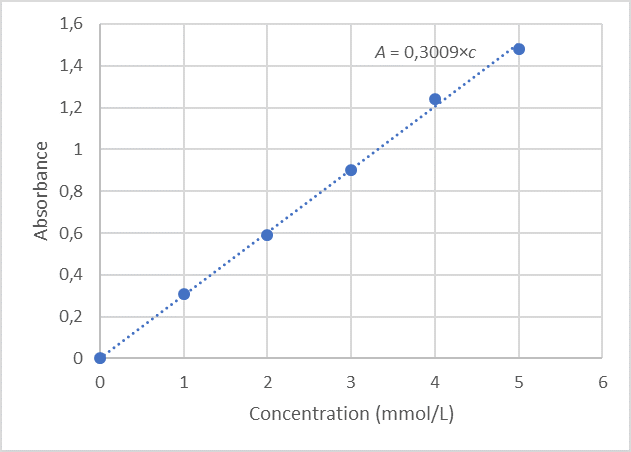
3. $*c = A/k =*$ 1,12/0,30 = 3,7 mmol·L-1.
Remarque : on aurait pu faire une lecture graphique, mais c’est moins précis.
Eau potable ou non ?
Le paranitrophénol (PNP) est un polluant organique qui se forme lors de la biodégradation de certains pesticides. Sa formule brute est $*\ce{C6H5NO3}*$.
La valeur maximale de la concentration en PNP d’une eau potable autorisée par la commission européenne est 0,1 µg·L-1. En revanche, le seuil fixé par l’agence américaine de protection environnemental EPA est 60 µg·L-1.
Résolution de problème
Répondre de manière argumentée à la question suivante :
L’eau analysée est-elle potable ?
Pour construire et développer votre argumentation, vous mobiliserez vos connaissances, vous vous aiderez des deux documents fournis, et vous répondrez au préalable à la question suivante :
Pourquoi est-il justifié de choisir une radiation visible plutôt qu’une radiation ultraviolette pour les mesures d’absorbance ?
Document 1 : Protocole de l’analyse
On procède tout d’abord à une évaporation de l’eau E de manière à accroître fortement la concentration en PNP. La solution S ainsi obtenue est cent fois plus concentrée que l’eau E.
À partir d’une solution aqueuse S0 de paranitrophénol de concentration $*C_0*$ = 100 mg·L-1, on prépare cinq solutions filles Si de volume $*V*$ = 100,0 mL en prélevant un volume $*V_i*$ de solution S0 complété à 100,0 mL par une solution tampon* de pH = 10.
On règle le spectrophotomètre sur la longueur d’onde $*\lambda*$ = 400 nm. On effectue le blanc de telle manière que l’absorbance soit nulle avec la solution tampon de pH = 10.
On mesure l’absorbance des différentes solutions Si préparées.
Les résultats des mesures sont regroupés dans le tableau suivant :
| Solution | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| $*V_i*$ (mL) | 1,0 | 2,0 | 3,0 | 5,0 | 7,5 |
| $*A*$ | 0,128 | 0,255 | 0,386 | 0,637 | 0,955 |
On mélange 50,0 mL de la solution S avec 50,0 mL de solution tampon de pH = 10 puis on mesure l’absorbance de la solution S’ ainsi obtenue.
On obtient une absorbance $*A'*$ = 0,570.
* Une solution tampon permet de fixer le pH du mélange auquel elle est ajoutée.
Document 2 : Spectres d’absorption de solutions aqueuses de PNP en milieu acide et en milieu basique
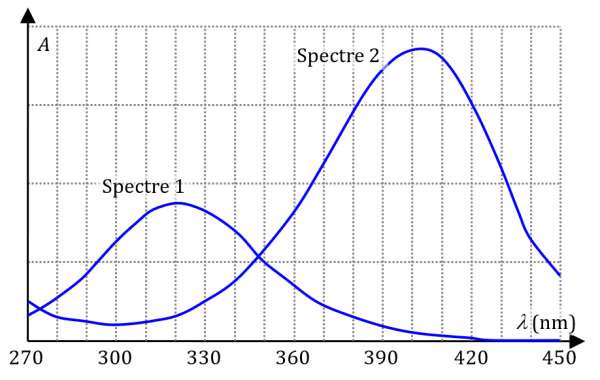
Spectre 1 : solution aqueuse de paranitrophénol à pH = 5.
Spectre 2 : solution aqueuse de paranitrophénol à pH = 10.
Correction
Question préalable
Lors de l’expérience, le PNP est placé dans des solutions dont le pH vaut 10.
Son absorbance est donc donnée par le spectre n°2.
Le maximum d’absorbance de ce spectre se trouve à 400 nm environ.
C’est pour cette raison que l’on choisit cette longueur d’onde, qui se trouve dans le visible, pour réaliser les mesures d’absorbance.
Réponse à la problématique
La potabilité de l’eau dépend de sa concentration en PNP.
Celle-ci est mesurée en réalisant un dosage spectrophotométrique. La première étape de ce dosage consiste à tracer la droite d’étlonnage qui va donner $*A = f(c)*$. Il faut donc commencer par tracer ce graphique à l’aide des données de l’énoncée.
La concentration des solutions étalons Si ne sont pas donnée directement. Il faut donc les calculer.
Concentration en PNP de la solution S1 : S1 est réalisée par dilution d’une solution-mère S0 de concentration 100 mg·L-1. En utilisant la relation de dilution $*C_M·V_M = C_F·V_F*$, on obtient la relation suivante : $µ C_1 = \frac{C_0V_0}{V_1} = \frac{100×1}{100} µ$
D’où $*C_1*$ = 1 mg·L-1.De la même manière, on obtient que $*C_2*$ = 2 mg·L-1, etc. Inutile de refaire le calcul pour chaque solution. On résume les résultats dans un tableau.
| Solution | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| $*V_i*$ (mL) | 1,0 | 2,0 | 3,0 | 5,0 | 7,5 |
| $*C_i*$ (mg·L-1) | 1,0 | 2,0 | 3,0 | 5,0 | 7,5 |
On trace le graphique $*A = f (c)*$
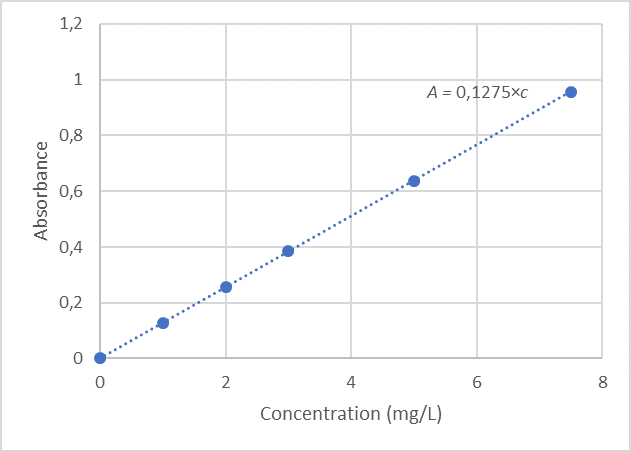
Soit $*c*$ la concentration en PNP de l’eau du robinet. La concentration de S en PNP est 100 fois plus grande.
Puis on obtient S’ en diluant d’un facteur 2 la solution S, donc la concentration $*c_{S'}*$ en PNP de S’ vaut $*c_{S'}*$ = 50×$*c*$.
L’absorbance de S’ vaut 0,570, donc $*c_{S'}*$ = 0,570/0,1275 = 4,47 mg/L.
Et donc $*c*$ = 89 µg/L.
Cette eau n’est donc pas potable, ni aux Etats-Unis (limite de 60 µg·L-1), ni en Europe (limite de 0,1 µg·L-1).
Remarque : là encore on peut faire une lecture graphique si on a tracé le graphique à la main. Ou encore, on peut calculer une valeur moyenne de $*k*$ à partir des différents couples ($*A*$ ; $*C_i*$). Tout dépend du temps dont on dispose et si on a accès à un ordinateur ou pas.
Révision & entraînement
Dosage spectro du bleu patenté
On souhaite déterminer la concentration en bleu patenté d’une solution de bain de bouche. Cette solution a une couleur bleu-cyan.
Le bleu patenté est un colorant alimentaire dont le spectre d’absorption est donné ci-dessous.
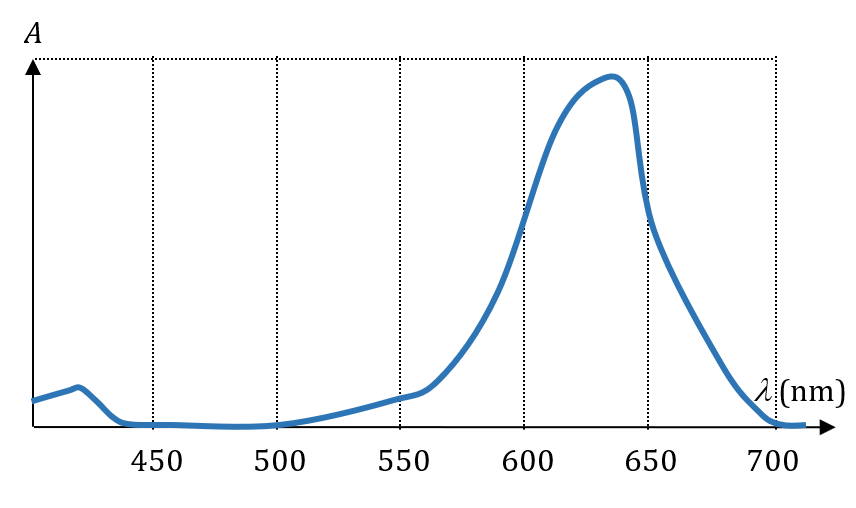
Pour réaliser ce dosage, on a préparé 5 solutions étalons à partir d’une solution-mère S de concentration 4 µmol·L-1 en bleu patenté, puis on a mesuré leur absorbance $*A*$ à la longueur d’onde idéale (voir question 2).
| Solutions filles Si | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| $*c*$ (µmol·L-1) | 0,40 | 0,80 | 1,20 | 1,60 | 2,00 |
| Absorbance $*A*$ | 0,064 | 0,133 | 0,194 | 0,255 | 0,319 |
On trace le graphique $*A = f(c)*$ sur un tableur. Le graphique est reproduit ci-dessous.
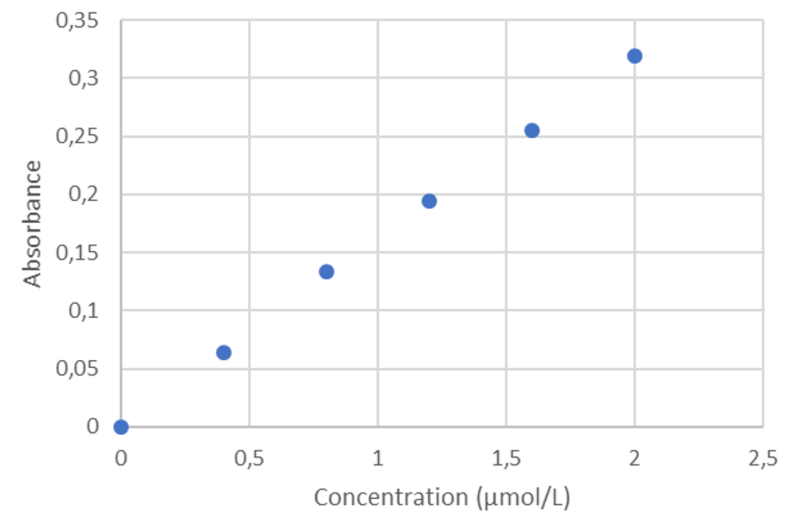
Le mesure de l’absorbance de la solution de bain de bouche donne $*A*$ = 0,232 dans les mêmes conditions que pour les solutions filles.

1. En quoi le spectre ci-dessus est-il cohérent avec la couleur bleue de la molécule ?
2. Quelle longueur d’onde choisir pour réaliser le dosage spectrophotométrique ? Justifier.
3. Expliquer comment réaliser 50 mL de S1 à partir de S.
4. Quelle est la concentration en bleu patenté de la solution pour bain de bouche ? Vous expliquerez votre méthode pour la déterminer précisément.
Correction
1. Absorbance forte entre 600 et 650 nm (orange). Donc la solution a la couleur complémentaire du orange : bleu-roi (entre cyan et bleu).
2. Maximum d’absorbance à 620 – 640 nm. C’est cette longueur d’onde qu’il faut choisir.
3. S1 est dix fois moins concentrée que S. Il faut donc 5 mL de S, prélevé à la pipette jaugée, que l’on verse dans une fiole jaugée de 50 mL.
Puis on complète jusqu’au trait de jauge avec de l’eau distillée.
4. Deux méthodes : lecture graphique ou calcul du coefficient directeur de la droite de tendance.
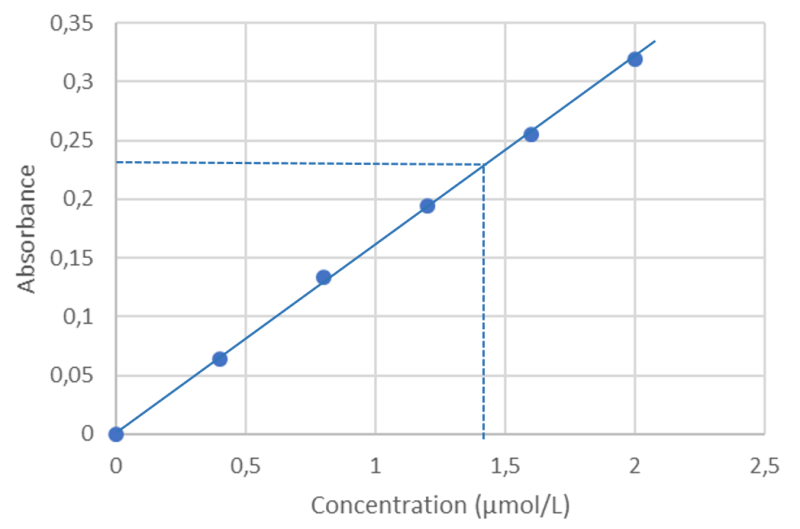
Par lecture graphique (il faut tracer à la main la droite de tendance) : on lit environ 1,45 µmol/L.
Par calcul du coefficient directeur :
la droite de tendance passe par les points (0 ; 0) et (2 ; 0,325).
Soit un coefficient directeur $*k*$ = 0,325/2 ≃ 0,16 L·µmol-1.
$*c = A/k =*$ 0,232 / 0,16 = 1,45 µmol·L-1.
Suivi d’une réaction
L’eau oxygénée $*\ce{H2O2}*$ réagit lentement avec les ions iodure $*\ce{I–}*$ en présence d’ions $*\ce{H+}*$ selon la réaction d’équation : $µ \ce{H2O2(aq) + 2I–(aq) + 2H+(aq) \rightarrow I2(aq) + 2 H2O(ℓ)} µ$
La seule espèce colorée présente dans le mélange est le diiode $*\ce{I2(aq)}*$. On peut donc suivre l’évolution de cette réaction par spectrophotométrie.
Données
- Masse molaire de l’iode : $*M(\ce{I})*$ = 126,9 g·mol-1

1. Couleur du diiode et choix de la longueur d’onde de travail
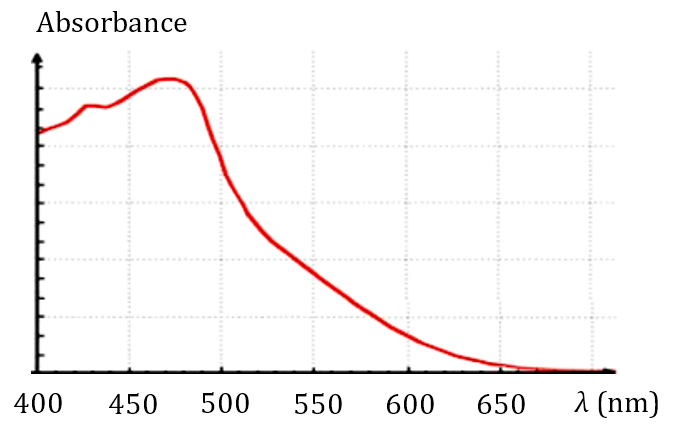
1.1. Le diiode en solution aqueuse est jaune-orangé. Justifier cette couleur à partir de son spectre d’absorption.
1.2. On dispose seulement de deux filtres pour le spectrophotomètre. L’un de 500 nm et l’autre de 600 nm. Lequel choisir ? Justifier.
2. Courbe d’étalonnage
On a réalisé différentes solutions de $*\ce{I2}*$ et mesurer leur absorbance à 500 nm. Les résultats obtenus ont permis d’obtenir le graphique ci-dessous.
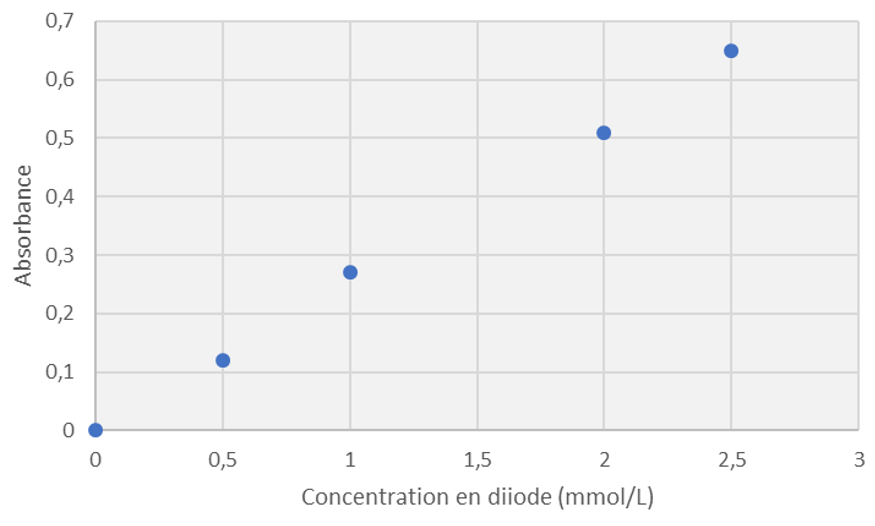
2.1. Ce graphique est-il en accord avec la loi de Beer-Lambert ? Justifier.
2.2. Montrer que $*k*$ = 0,26 L·mmol-1.
3. Suivi de la réaction
Une solution contenant de l’eau oxygénée $*\ce{H2O2(aq)}*$, des ions iodure $*\ce{I–(aq)}*$ et des ions $*\ce{H+(aq)}*$ est placée dans le spectrophotomètre. On mesure son absorbance à 500 nm pendant 10 minutes, on obtient le graphique suivant :
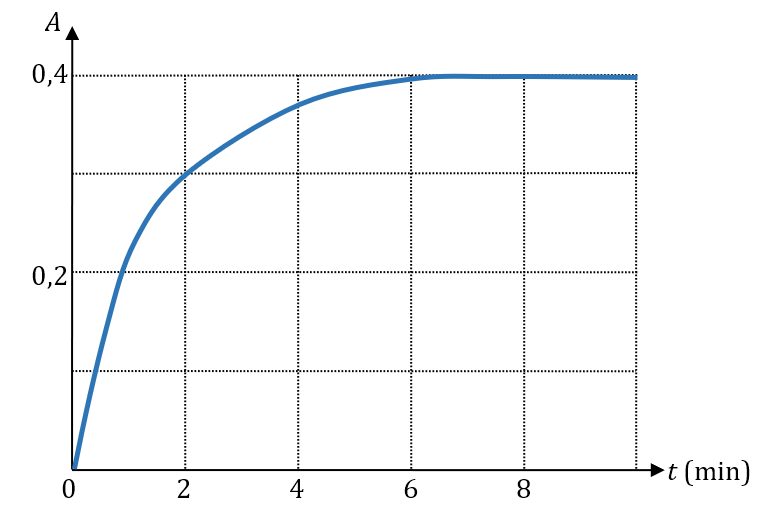
3.1. L’état final est atteint quand la concentration en diiode n’évolue plus. Quelle est alors sa concentration ?
3.2. Le volume de la solution où se déroule la réaction vaut $*V*$ = 100 mL. Quelle est alors la quantité de matière de diiode formée à l’état final ?
3.3. Quelle masse de diiode cela représente-t-il ?
Correction
1.1. Le maximum d’absorption du diiode se situe autour de 470 nm. La couleur opposée sur le cercle chromatique correspond à la zone de transition entre le jaune et le orange.
1.2. À 600 nm, l’absorbance est très faible. Il faut donc choisir le filtre à 500 nm.
2.1. On remarque que les points forment une droite qui passe par l’origine. L’absorbance est donc proportionnelle à la concentration, ce que dit la loi de Beer-Lambert ($*A = k·c*$).
2.2. Il faut tracer la droite qui passe « au plus près » de tous les points.
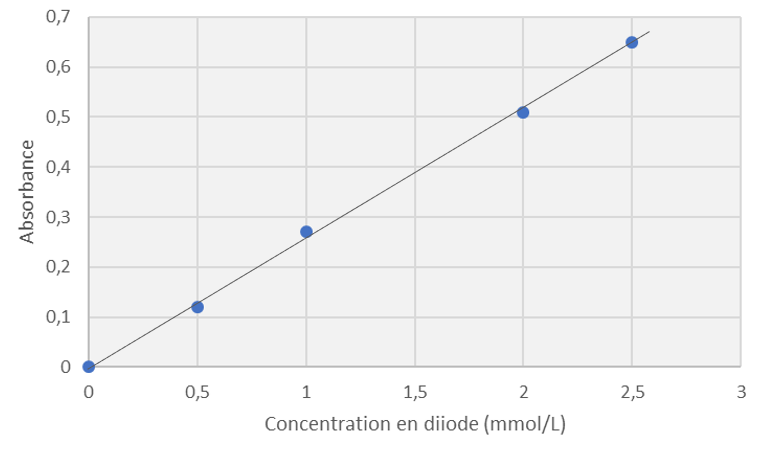
Cette droite passe par le point (2,5 ; 0,65), donc $*k*$ = 0,65÷2,5 = 0,26 L·mmol-1.
3.1. Lorsque l’état final est atteint, $*A*$ = 0,40, donc $*c*$ = 0,40÷0,26 ≃ 1,54 mmol·L-1.
3.2. $*n = cV =*$ 1,54·10-3×100·10-3 = 1,54·10-4 mol.
3.3. $*m = nM =*$ 1,54·10-4×(126,9×2) = 3,9·10-2 g.