C3. Avancement de réaction
Avancement de réaction
- Décrire qualitativement l’évolution des quantités de matière des espèces chimiques lors d’une transformation.
Équation-bilan d’une réaction chimique
L’équation-bilan d’une réaction chimique, que vous connaissez depuis longtemps, donne deux informations distinctes :
- La nature des espèces chimiques mises en jeu au cours de la réaction (réactifs et produits).
- La proportion en quantité de matière liant toutes ces espèces entre elles.
Exemple : combustion du méthane
Vous connaissez bien cette réaction, que vous avez déjà vu au collège. Le méthane, c’est le « gaz naturel » que l’on utilise pour se chauffer ou pour faire fonctionner certains véhicules.
$µ \ce{CH4 + 2 O2 \rightarrow CO2 + 2 H2O}µ$
Dans cet exemple, les réactifs sont $*\ce{CH4}*$ et $*\ce{O2}*$ et les produits de la réaction sont $*\ce{CO2}*$ et $*\ce{H2O}*$
Les proportions liant ces différentes espèces chimiques sont :
qdm de $*\ce{O2}*$ consommée = 2 × qdm de $*\ce{CH4}*$ consommée
qdm de $*\ce{CO2}*$ produite = qdm de $*\ce{CH4}*$ consommée
qdm d’eau produite = 2 × qdm de $*\ce{CH4}*$ consommée
Grâce à ces informations, on peut prévoir les qdm de réactif en excès et les qdm des produits formés à la fin de la réaction. C’est l’objet de tout le chapitre. 😊
Avancement de réaction
L’avancement de réaction (notée $*x*$) est une grandeur qui indique « combien de fois la réaction s’est faite » et donc les qdm de réactifs consommés et les qdm de produits formés à un stade donné de la réaction. Son unité est la mole.
Reprenons l’exemple de la combustion du méthane.
| Avancement (mol) |
qdm $*\ce{CH4}*$ conso. |
qdm $*\ce{O2}*$ conso. |
qdm $*\ce{CO2}*$ produite |
qdm $*\ce{H2O}*$ produite |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 1 | 2 |
| 2 | 2 | 4 | 2 | 4 |
| $*x*$ | $*x*$ | 2$*x*$ | $*x*$ | 2$*x*$ |
Combustion du méthane
On fait brûler 1,0 kg de méthane. Dans les conditions de l’expérience, le volume molaire des gaz vaut $*V_M*$ = 24 L·mol-1.
Données : $*M_\ce{CH4}*$ = 16 g·mol-1 ; $*M_\ce{H2O}*$ = 18 g·mol-1 ; $*M_\ce{CO2}*$ = 44 g·mol-1
1. Calculer le volume d’air nécessaire à cette combustion (l’air contient 20 % de $*\ce{O2}*$)
2. Calculer les masses de $*\ce{CO2}*$ et d’eau produites.
Correction
1. Qdm de $*\ce{CH4}*$ = $*\frac mM*$ = 1000/16 = 62,5 mol.
Donc il faut 2×62,5 = 125 mol de $*\ce{O2}*$.
Cela représente un volume de 125×24 = 3000 L (soit 3 m3).
Comme l’air ne contient que 20 % de dioxygène, cela signifie qu’il faut un volume total de 3/0,2 = 15 m3 d’air.
2. Cette combustion produit 62,5 mol de $*\ce{CO2}*$ et 125 mol d’eau.
En masse, cela représente 62,5×44 = 2750 g de $*\ce{CO2}*$ et 125×18 = 2250 g d’eau.
Tableau d’avancement
- Établir le tableau d’avancement d’une transformation chimique.
- Déterminer la composition du système dans l’état final en fonction de sa composition initiale pour une transformation considérée comme totale.
- Déterminer l’avancement final d’une réaction à partir de la description de l’état final et comparer à l’avancement maximal.
- Capacité mathématique : utiliser une équation linéaire du premier degré.
Il existe un outil pour pouvoir résoudre simplement l’exercice précédent. Cet outil s’appelle le tableau d’avancement.
TP Simulation numérique de l’avancement d’une réaction
- Capacité numérique : déterminer la composition de l’état final d’un système siège d’une transformation chimique totale à l’aide d’un langage de programmation.
Objectif : écrire un programme en Python qui prévoit la composition finale d’un système où se déroule une réaction chimique totale.
Rappels concernant quelques bases de Python
- Créer une variable et lui attribuer une valeur :
a = 1 - Créer une variable calculée à partir d’une autre variable :
b = a + 2.5 - Afficher une variable :
print(b) - Afficher plusieurs variables et du texte :
print("a = ", a, "et b = ", b) - Choisir la plus petite de 2 variables :
c = min(a,b)
Partie 1 : combustion du dihydrogène
Soit la réaction : $µ \ce{2 H2 + O2 \rightarrow 2 H2O} µ$
1. Écrire un programme qui va calculer et afficher les qdm de $*\ce{H2}*$ et de $*\ce{O2}*$ restantes ainsi que la qdm d’eau produite à partir des qdm de $*\ce{H2}*$ et de $*\ce{O2}*$ initiales et de l’avancement $*x*$.
Entrées du programme (les valeurs qu’il faut lui fournir) : $* n(\ce{H2})_i*$ , $* n(\ce{O2})_i*$ , $*x*$
Sorties du programme (les valeurs qu’il calcule) : $* n(\ce{H2})*$ , $* n(\ce{O2})*$ , $* n(\ce{H2O})*$
Voici une structure possible du code, à compléter avec les calculs nécessaires.
n1i = ___ # qdm initiale H2
n2i = ___ # qdm initiale O2
x = ___ # avancement
n1 = ___ # qdm H2 pour x
n2 = ___ # qdm O2 pour x
n3 = ___ # qdm eau pour x
print("H2 : ", n1, " mol ; O2 : ", n2, " mol ; eau ", n3, " mol")
Que se passe-t-il si on prend une valeur de $*x*$ trop grande ? En quoi est-ce un problème d’un point de vue chimique ?
2. Modifier votre code pour que le programme calcule et affiche la valeur maximale de $*x*$, notée $*x_{\text{max}}*$, ainsi que les qdm des espèces restantes.
Entrées du programme : $* n(\ce{H2})_i*$ , $* n(\ce{O2})_i*$
Sorties du programme : $* n(\ce{H2})*$ , $* n(\ce{O2})*$ , $* n(\ce{H2O})*$ , $*x_\max*$
Partie 2 : cas général
Soit la réaction générale : $µ a\text{A} + b\text{B} \rightarrow c\text{C} + d\text{D} µ$
A, B, C et D sont des espèces chimiques.
$*a*$, $*b*$, $*c*$ et $*d*$ sont les nombres stœchiométriques associés à ces espèces.
Écrire un programme qui va calculer les qdm de A, B, C et D en fin de réaction en fonction des qdm initiales de A et de B et des nombres stœchiométriques $*a*$, $*b*$, $*c*$ et $*d*$.
Éléments de correction
# Valeurs à renseigner -------------
nAi = 10 # qdm initiale A
nBi = 3 # qdm initiale B
a = 1 # nbr stoechiométrique de A
b = 2 # nbr stoechiométrique de B
c = 1 # nbr stoechiométrique de C
d = 2 # nbr stoechiométrique de D
#-----------------------------------
x_max = min(nAi/a , nBi/b)
nA = nAi-a*x_max # qdm A pour x
nB = nBi-b*x_max # qdm B pour x
nC = c*x_max # qdm C pour x
nD = d*x_max # qdm D pour x
print('A', nA,'mol ; B', nB, 'mol ; C',
nC, 'mol ; D', nD , 'mol ; x_max', x_max, 'mol')
Écriture du tableau d’avancement
Un tableau d’avancement contient en général 4 lignes et $*n*$+1 colonnes, $*n*$ étant le nombre de réactifs et de produits impliqués dans la réaction.
| $*x*$ (mol) | $*\ce{\quad $a$A \quad + \quad $b$B \quad \rightarrow \quad $c$C \quad + \quad $d$D \quad}*$ | |||
|---|---|---|---|---|
| 0 | $*n_{\text{A}i}*$ | $*n_{\text{B}i}*$ | $*n_{\text{C}i}*$ | $*n_{\text{D}i}*$ |
| $*x*$ | $*n_{\text{A}i}-ax*$ | $*n_{\text{B}i}-bx*$ | $*n_{\text{C}i}+cx*$ | $*n_{\text{D}i}+dx*$ |
| $*x_f*$ = | $*n_{\text{A}i} -ax_f*$ | $*n_{\text{B}i}-bx_f*$ | $*n_{\text{C}i} +cx_f*$ | $*n_{\text{D}i}+dx_f*$ |
✋ Il est impératif de bien maîtriser toutes les formules portant sur les qdm pour réaliser un tableau d’avancement.
1e ligne : on précise toujours l’unité de l’avancement (mol, mmol, …). On écrit ensuite l’équation-bilan.
2e ligne : c’est la ligne de l’état initial (l’avancement $*x*$ vaut 0). Les quantités de matière initiale des produits ($*n_{\text{C}i}*$ et $*n_{\text{D}i}*$) valent souvent 0, mais ce n’est pas une obligation. Il est en général demandé de calculer les qdm initiales des produits à partir de grandeur mesurable (masse, volume, concentration…).
3e ligne : pour une valeur quelconque $*x*$. La 2e et la 3e lignes peuvent être fusionnées.
4e ligne : ligne de l’état final ($*x = x_f*$) (voir le paragraphe suivant pour trouver $*x_f*$). Il faut écrire la valeur des qdm finales de réactifs et de produits dans cette ligne, ainsi que la valeur de $*x_f*$. C’est ce qu’on appelle faire un bilan de matière.
Avancement maximum $*x_{\max}*$
Proportions stoechiométriques
On dit que les réactifs sont en proportion stoechiométriques si, pour $*x = x_{\max}*$, tous les réactifs sont épuisés.
Réactions totale et non totale
Certaines réactions ne sont pas totales : elles ne se déroulent pas jusqu’à épuisement d’un des réactifs, mais s’arrêtent avant. On dit que ce sont des réactions non totales ou limitées. Leur avancement final $*x_f*$ ne peut pas être déduit des qdm initiales de réactifs.
- Réaction totale : $*x_f = x_{\max}*$
- Réaction non totale : $*x_f \lt x_{\max}*$
Oxydation du fer
Le fer ($*\ce{Fe}*$) réagit à chaud avec le dioxygène de l’air pour donner de l’oxyde de fer (III) $*\ce{Fe2O3}*$. On souhaite oxyder 100 g de fer par le dioxgène de l’air. La réaction est totale.
Données : $*M(\ce{Fe})*$ = 55,8 g·mol-1 ; $*M(\ce{O})*$ = 16,0 g·mol-1.
1. Quel est le réactif limitant ici ?
2. Construire le tableau d’avancement pour faire un bilan de matière en fin de réaction.
3. En déduire la masse d’oxyde de fer obtenu.
Correction
1. Il s’agit de $*\ce{Fe}*$ car nous avons tout le $*\ce{O2}*$ de l’atmosphère à disposition.
2. Quantité initiale de $*\ce{Fe}*$ : $*n = m / M =*$ 1,79 mol
Il faut également équilibrer la réaction.
| $*x*$ (mol) | $*\ce{2 Fe}*$ $*+*$ $*\ce{1,5 O2}*$ $*\rightarrow*$ $*\ce{Fe2O3}*$ |
||
|---|---|---|---|
| 0 | 1,79 | infini | 0 |
| $*x*$ | 1,79$*-2x*$ | $*x*$ | |
| $*x_f*$ = 0,90 | 0 | 0,90 | |
$*x_{\max}*$ = 1,79 / 2 = 0,90 mol
3. Masse molaire de l’oxyde de fer : $*M(\ce{Fe2O3})*$ = 55,8×2 + 16×3 = 159,6 g·mol-1.
Masse d’oxyde de fer obtenu : $*m = n×M =*$ 0,90×159,6 = 144 g
Poudre à canon

On nomme poudre noire, ou poudre à canon, un mélange explosif de salpêtre ($*\ce{KNO3}*$) (du latin salpetrae signifiant « sel de pierre »), de soufre ($*\ce{S}*$) et de charbon de bois ($*\ce{C}*$). La plupart des historiens pensent que la poudre à canon fut inventée en Chine vers le VIIe siècle.
L’équation de la combustion de la poudre à canon est la suivante : $µ \ce{2 KNO3 + 3 C + S \rightarrow K2S + 3 CO2 + N2} µ$ Cette réaction est totale.
Au XIVe siècle et XVe siècle, la composition était (en masse) : 6 parties de salpêtre (75 %) pour une partie de soufre (12,5 %) et une partie de carbone sous forme de charbon de bois (12,5 %).
Cette recette était-elle optimale ?
Masses molaires en g·mol-1
$*M(\ce{K})*$ = 39 ; $*M(\ce{N})*$ = 14 ; $*M(\ce{O})*$ = 16 ; $*M(\ce{C})*$ = 12 ; $*M(\ce{S})*$ = 32Correction
Raisonnons sur 100 g de poudre. On a 75 g de $*\ce{KNO3}*$, 12,5 g de $*\ce{C}*$ et 12,5 g de $*\ce{S}*$.
Quantité de matière de réactifs
$*M(\ce{KNO3})*$ = 39 + 14 + 16×3 = 101 g·mol-1
donc $*n(\ce{KNO3}) = m/M =*$ 75/101 = 0,743 mol.
$*n(\ce{C})*$ = 12,5/12 = 1,042 mol
$*n(\ce{S})*$ = 12,5/32 = 0,391 mol
Tableau d’avancement
| $*x*$ (mol) | $*\ce{2KNO3}*$ $*+*$ $*\ce{3C}*$ $*+*$ $*\ce{S}*$ $*\rightarrow*$ $*\ce{K2S}*$ $*+*$ $*\ce{3 CO2}*$ $*+*$ $*\ce{N2}*$ |
|||||
|---|---|---|---|---|---|---|
| 0 | 0,743 | 1,042 | 0,391 | 0 | 0 | 0 |
| $*x*$ | 0,743 $* - 2x*$ | 1,042 $*- 3x*$ | 0,391 $*- x*$ | $*x*$ | $*3x*$ | $*x*$ |
| $*x_f*$ = 0,347 | 0,049 | 0 | 0,044 | 0,347 | 1,042 | 0,347 |
On voit qu’en fin de réaction, il reste encore un peu de $*\ce{KNO3}*$ et de $*\ce{S}*$, mais très peu. Le mélange n’est donc pas parfaitement optimal, mais il n’en est pas loin. Plutôt impressionnant pour une technologie du Moyen-Âge.
Réaction d’estérification
On mélange 10,0 mL d’éthanol $*\ce{C2H6O}*$ ($*d*$ = 0,78) et 10,7 mL d’acide éthanoïque $*\ce{C2H4O2}*$ ($*d*$ = 1,05). Il se forme de l’éthanoate d’éthyle ($*\ce{C4H8O2}*$) et de l’eau selon une réaction non totale appelée réaction d’estérification. La qdm finale d’éthanoate d’éthyle vaut 0,11 mol.
1. Calculer l’avancement $*x_f*$ de cette réaction.
2. Calculer l’avancement maximum $*x_{\max}*$ de la réaction, c’est-à-dire l’avancement de la réaction si celle-ci était totale.
3. Quel pourcentage de $*x_{\max}*$ représente $*x_f*$ ?
Correction
1. 1e étape : tableau d’avancement de la réaction (et calcul des qdm initiales de réactifs).
Éthanol : $*n_{1,i} = m/M =*$ 10×0,78/46 = 0,17 mol
Acide éthanoïque : $*n_{2,i} = m/M =*$ 10,7×1,05/60 = 0,19 mol
| $*x*$ (mol) | $*\ce{C2H6O}*$ $*+*$ $*\ce{C2H4O2}*$ $*\rightleftarrows*$ $*\ce{C2H3O2C2H5}*$ $*+*$ $*\ce{ H2O}*$ |
|||
|---|---|---|---|---|
| 0 | 0,17 | 0,19 | 0 | 0 |
| $*x*$ | 0,17 $*-x*$ | 0,19 $*-x*$ | $*x*$ | $*x*$ |
| $*x_f*$ = | 0,11 | |||
On voit sur le tableau d’avancement que la qdm d’éthaonate d’éthyle est égale à l’avancement $*x*$. Donc si la qdm finale d’éthanoate d’éthyle vaut 0,11 mol, alors $*x_f*$ = 0,11 mol.
2. Si la réaction était totale, l’avancement pourrait aller jusqu’à la valeur $*x_{\max}*$ = 0,17 mol.
3. $*x_f / x_{\max} = 0,11/0,17 \simeq*$ 0,65. Donc $*x_f*$ représente 65 % de $*x_{\max}*$.
Révision & entraînement
Composition de l’air
Cet exercice a été donné en devoir en 2020/2021
En 1775, Lavoisier a mis en évidence que l’air était un mélange de gaz et qu’il contenait du dioxygène. Il a fait bouillir 122 g de mercure Hg dans une cornue reliée à une cloche contenant 0,80 L d’air (schéma ci-dessous). Le mercure se recouvre d’une couche rouge : c’est de l’oxyde de mercure de formule HgO, il en a obtenu 2,8 g.
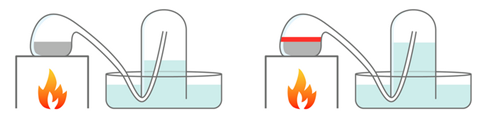
Données
- $*M(\ce{Hg})*$ = 200,6 g·mol-1
- $*M(\ce{O})*$ = 16,0 g·mol-1
- Volume molaire d’un gaz dans les conditions de l’expérience : 25 L·mol-1
1. Écrire l’équation-bilan de la réaction chimique entre le dioxygène et le mercure.
2. Calculer la quantité de matière finale d’oxyde de mercure formé.
3. Justifiez que, d’après les résultats de l’expérience, le dioxygène est le réactif par défaut.
4. Dresser le tableau d’avancement de la réaction. La quantité initiale de $*\ce{O2}*$ est inconnue. Vous la noterez $*n_{i\ce{O2}}*$.
5. Donner la valeur de l’avancement final et en déduire la quantité initiale de $*\ce{O2}*$.
6. Calculer la quantité de matière d’air initialement présente dans la cloche et calculer la proportion de dioxygène présent dans l’air.
7. Calculer la masse de mercure restante en fin de réaction.
Correction
1. $*\ce{Hg}*$ + $* \frac 12 \ce{O2}*$ → $*\ce{HgO}*$
2. $*n(\ce{HgO})*$ = $*\frac mM *$ = 2,8÷216,6 = 12,9 mmol.
3. À la fin de la réaction, il reste du mercure qui n’a pas réagi.
4. Tableau d’avancement
| $*x*$ (mol) | $*\ce{ \quad \;\; Hg \quad + \quad \frac 12 O2 \; \rightarrow \;\; HgO}*$ | ||
|---|---|---|---|
| 0 | 0,608 | $*n_{i\ce{O2}}*$ | 0 |
| $*x*$ | 0,608 – $*x*$ | $*n_{i\ce{O2}}*$ – 0,5$*x*$ | $*x*$ |
| $*x_f*$ | 0,608 – $*x_f*$ | 0 | $*x_f*$ = 0,0129 |
5. $*x_f*$ = 0,0129 mol, donc $*n_{i\ce{O2}}*$ = 0,00646 mol.
6. $*n_{air}*$ = 0,8/25 = 0,032 mol. Proportion de $*\ce{O2}*$ : 0,00646/0,032 = 0,20 (soit 20 %)
7. $*m(\ce{Hg})*$ = (0,608 – 0,0129)×200,6 = 119,4 g
Tableau d’avancement en Python
Cet exercice a été donné en devoir en 2020/2021
Soit la réaction suivante : $µ \ce{2 MnO4– + 5 H2C2O4 + 6 H+ \rightarrow 2 Mn^2+ + 10 CO2 + 8 H2O} µ$ On souhaite coder un programme en Python qui permet de prévoir l’état final du mélange, sachant que cette réaction est totale.
n1 = # qdm initiale de MnO4-
n2 = # qdm initiale de H2C2O4
n3 = # qdm initiale de H+
xmax1 = n1/2
xmax2 = _____
xmax3 = _____
xmax = min ( _____ )
n1f = _____
n2f = ______
n3f = ______
n4f = 2*xmax
n5f = 10*xmax
n6f = 8*xmax
1. À quoi correspondent les lignes 13, 14 et 15 ?
2. Compléter les lignes 6, 7, 8, 10, 11 et 12.
Correction
1. Respectivement qdm finale de $*\ce{Mn2+}*$ ; $*\ce{CO2}*$ et $*\ce{H2O}*$
2. Lignes à compléter
6. xmax2 = n2/5
7. xmax3 = n3/6
8. xmax = min (xmax1, xmax2, xmax3)
10. n1f = n1 – 2*xmax
11. n2f = n2 – 5*xmax
12. n3f = n3 – 6*xmax