C5. Titrages
Titrer, en chimie, c’est déterminer la concentration d’une solution en utilisant une réaction chimique. Un titrage est donc une catégorie de dosage : il s’agit d’un dosage qui implique l’utilisation d’une réaction, appelée « réaction de titrage ».
Ce chapitre est court, mais il est extrêmement important pour le reste de votre scolarité.
TP Titrage du diiode
- Réaliser un titrage direct avec repérage colorimétrique de l’équivalence pour déterminer la quantité de matière d’une espèce dans un échantillon.
- Mettre en œuvre des transformations modélisées par des réactions d’oxydoréduction.
Objectif du TP : titrer une solution de diiode $*\ce{I2(aq)}*$ par une solution de thiosulfate de sodium ($*\ce{2Na^+(aq) + S2O3^2-(aq)}*$)
Question préliminaire
Un titrage implique la réaction entre un réactif titré (celui dont on cherche à trouver la concentration) qui est ici le diiode, et un réactif titrant, qui est ici l’ion thiosulfate $*\ce{S2O3^2-}*$.
Sachant que cette réaction est une réaction d’oxydoréduction, que le diiode appartient au couple $*\ce{I2/I^-}*$ et que l’ion thiosulfate appartient au couple $*\ce{S4O6^2-/S2O3^2-}*$, trouver l’équation-bilan de la réaction de titrage.
Matériel disponible
- Solution de diiode $*\ce{I2(aq)}*$ de concentration inconnue $*C_1*$
- Solution de thiosulfate de sodium ($*\ce{2Na^+ + S2O3^2-}*$), $*C_2*$ = 4,8 mmol/L
- Iodex : indicateur coloré devient bleu en présence de diiode. Sa coloration est très intense, contrairement à celle du diiode.
- Dispositif de titrage ci-dessous
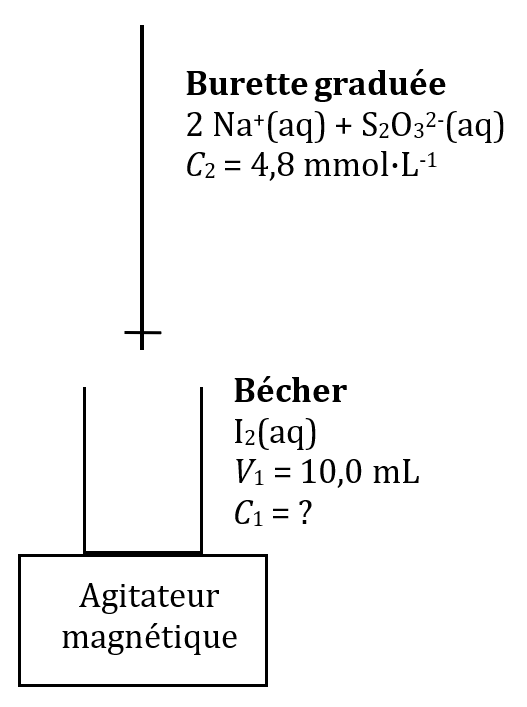
Tableau d’avancement de la réaction
1. Compléter le tableau d’avancement ci-dessous.
| Av. | $*\ce{\quad \ldots I_2 \qquad + \; \ldots S2O3^2- \quad \rightarrow \qquad \ldots \qquad + \qquad \ldots \qquad}*$ | |||
|---|---|---|---|---|
| 0 | $*C_1V_1*$ | $*C_2V_2*$ | 0 | 0 |
| $*x_\max*$ | ||||
2. Quelle relation doit-on avoir entre $*C_1*$ , $*V_1*$ , $*C_2*$ et $*V_2*$ pour que le mélange soit stœchiométrique ?
Protocole
- Mettre 20,0 mL de solution de $*\ce{I2}*$ dans un bécher propre avec une pipette jaugée.
- Préparer la burette avec la solution de thiosulfate de sodium.
- Mettre l’agitateur magnétique dans le bécher et démarrer l’agitation douce.
- Verser petit à petit la solution de thiosulfate de sodium dans le bécher.
- Quand le mélange dans le bécher devient très peu coloré, ajouter une pointe de spatule de Iodex.
- Continuer à verser le thiosulfate de sodium en vous arrêtant dès que la coloration disparaît. Noter le volume $*V_{2E}*$ de solution de thiosulfate versé.
Exploitation du titrage
3. Qu’y a-t-il de particulier lorsque vous avez atteint le volume $*V_{2E}*$ du point de vue des quantités de matières de réactifs ?
4. Calculer la concentration $*C_1*$ de la solution de diiode ?
5. Estimer l’incertitude sur la valeur de $*C_1*$
Éléments de correction
1. Équation-bilan et tableau d’avancement
| Av. | $*\ce{\qquad \quad I_2 \qquad \; + \qquad 2 S2O3^2- \qquad \rightarrow \quad \qquad 2 I^- \qquad + \qquad S4O6^2- \qquad}*$ | |||
|---|---|---|---|---|
| 0 | $*C_1V_1*$ | $*C_2V_2*$ | 0 | 0 |
| $*x_\max*$ | $*C_1V_1 - x_\max*$ | $*C_2V_2 - 2 x_\max*$ | $*2x_\max*$ | $*x_\max*$ |
2. Pour un mélange stœchiométrique, il faut que pour $*x = x_\max*$ , $*C_1V_1 - x_\max*$ = 0 et $*C_2V_2 - 2 x_\max*$ = 0.
Donc $*C_2V_2*$ = $*2 C_1V_1*$
3. Lorsque $*V_2*$ = $*V_{2E}*$, on a introduit juste assez de $*\ce{S2O3^2-}*$ pour que tout le $*\ce{I2}*$ ait réagi.
4. Pour $*V_{2E}*$ = 10,5 mL, on trouve que $*C_1 = \frac{C_2V_{2E}}{2V_1} =*$ 2,38 mmol·L-1.
5. Pour estimer l’incertitude sur $*C_1*$, il faut estimer les incertitudes sur $*V_{2E}*$, $*V_1*$ et $*C_2*$.
• L’incertitude sur $*C_2*$ est donnée (vous ne pouvez pas estimer l’incertitude, ce n’est pas vous qui avez fait la solution) : $*\Delta C_2*$ = ± 0,05 mmol·L-1.
• L’incertitude sur $*v_1*$ est écrite sur la pipette jaugée (± 0,01 mL), mais comme vous n’êtes pas (encore) des pros 😊 et que la température de la salle de TP n’était pas la température nominale de la pipette, on peut multiplier cette incertitude par deux.
• L’incertitude sur $*V_{2E}*$ peut être assez large (zéro de la burette, perception de la décoloration, lecture du niveau sur la burette) : on va l’estimer à ± 0,2 mL.
On calcule $*C_{1\,\min} = \dfrac{C_{2\,\min}V_{2E\,\min}}{2V_{1\,\max}} =*$ 2,29 mmol·L-1.
De la même manière, on calcule $*C_{1\,\max}*$ = 2,45 mmol·L-1.
On est donc sûr que 2,29 ≤ mmol·L-1 $*C_1*$ ≤ 2,45 mmol·L-1.
Remarque : on verra plus tard dans l’année de méthodes de calculs d’incertitudes. Ce qu’on vient de voir n’est qu’une première approche.
Principe et montage expérimental
Définitions
Dosage : méthode permettant de déterminer une quantité de matière ou une concentration d’une espèce chimique donnée. Exemple : dosage spectrophotométrique vu au chapitre C2.
Titrage : méthode de dosage qui implique une réaction chimique entre le réactif à titrer (appelé réactif titré ou titré) et une autre espèce chimique (le réactif titrant ou titrant).
Montage expérimental
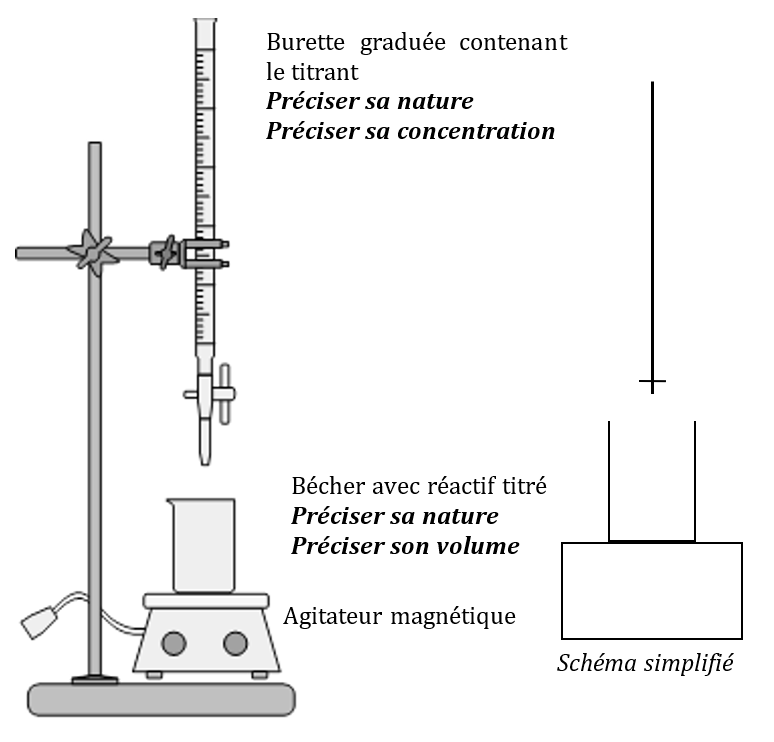
Principe
On ajoute peu à peu le titrant de concentration connue dans le bécher contenant le titré de volume connu.
On s’arrête lorsqu’on a introduit le titrant en proportions stœchiométriques avec le titré (c’est l’équivalence, voir plus loin).
Grâce au volume de réactif titrant versé à l’équivalence déterminé par l’expérience et connaissant l’équation-bilan de la réaction de titrage, on en déduit la concentration du titré.
Réaction de titrage
- Relier qualitativement l’évolution des quantités de matière de réactifs et de produits à l’état final au volume de solution titrante ajoutée.
Pour servir à un titrage, la réaction chimique entre le titrant et le titré doit respecter plusieurs critères.
- Elle doit être rapide (sinon, on ne sait pas quand arrêter l’ajout d’espèce titrante).
- Elle doit être totale (sinon, on ne dosera pas toute l’espèce à titrer mais seulement une partie).
- Elle doit être spécifique de l’espèce à titrer (si elle réagit une autre espèce, on ne peut pas déterminer la quantité de matière de l’espèce à titrer).
- L’équivalence doit être repérable (sinon on ne sait pas quand on est arrivé aux proportions stœchiométriques).
Équivalence
- Relier l’équivalence au changement de réactif limitant et à l’introduction des réactifs en proportions stœchiométriques.
- Établir la relation entre les quantités de matière de réactifs introduites pour atteindre l’équivalence.
- Expliquer ou prévoir le changement de couleur observé à l’équivalence d’un titrage mettant en jeu une espèce colorée.
Définition
L’équivalence est le moment ou le titrant et le titré ont été introduit en proportions stœchiométriques. Tout le titré a réagi et il n’y a pas de titrant introduit en excès.
Repérer l’équivalence
Il faut que ce moment soit parfaitement repérable. Pour cela, plusieurs techniques existent, qui dépendent de la nature de la réaction de titrage.
En première, on n’en voit qu’une seule : l’équivalence est repérée par un changement de couleur. Pour cela, on utilise généralement un indicateur coloré qui va changer la couleur du mélange réactionnel dans le bécher au moment où l’équivalence est atteinte.
Relation entre les quantité de matière à l’équivalence
Pour une réaction de titrage de la forme $*\ce{$a$A + $b$B \rightarrow $c$C + $d$D}*$, lorsque l’équivalence est atteinte, la relation entre la quantité initiale du réactif titré A, notée $*n_{0A}*$ et la quantité ajoutée à l’équivalence de titrant B notée $*n_{0B}*$ est : $µ \frac {n_{0A}}a = \frac {n_{0B}}b µ$
Révision & entraînement
Titrage de l’eau oxygénée
On réalise le titrage d’un volume $*V_1*$ = 20,0 mL d’une solution d’eau oxygénée $*\ce{H2O2}*$ par une solution de permanganate de potassium ($*\ce{K^+ + MnO4^–}*$) de concentration $*C_2*$ = 5,0 mmol·L-1.
Le volume de solution de permanganate versé à l’équivalence vaut $*V_{2E}*$ = 12,7 mL.
Données
- L’eau oxygénée appartient au couple $*\ce{O2/H2O2}*$
- L’ion permanganate appartient au couple $*\ce{MnO4^-/Mn^2+}*$
- Seul l’ion permanganate est coloré (coloration violette très intense).
1. Écrire l’équation-bilan de la réaction de titrage.
2. Faire le schéma du montage.
3. Expliquer comment repérer l’équivalence pour ce titrage.
4. Déterminer la concentration de la solution d’eau oxygénée.
Correction
1. Il faut d’abord trouver les demi-équations :
$*\ce{O2 + 2e^- + 2H^+ = H2O2}*$ (×5)
$*\ce{MnO4^- + 5e^- + 8H^+ = Mn^2+ + 4 H2O}*$ (×2)
On écrit ensuite l’équation-bilan de la réaction :
$*\ce{5 H2O2 + 2 MnO4^- + 16 H^+ \rightarrow 5O2 + 10 H^+ + 2 Mn^2+ + 8 H2O}*$
qu’on peut simplifier en :
$*\ce{5 H2O2 + 2 MnO4^- + 6 H^+ \rightarrow 5O2 + 2 Mn^2+ + 8 H2O}*$
2. Schéma du montage
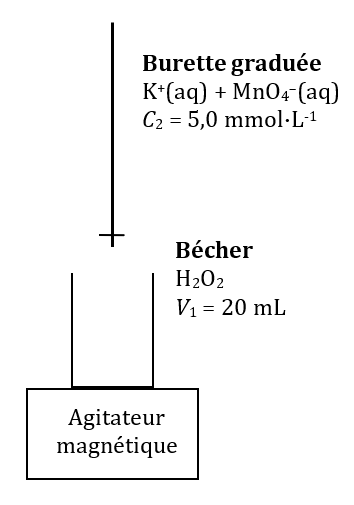
3. Avant l’équivalence, $*\ce{H2O2}*$ réagit avec l’ion $*\ce{MnO4^-}*$ et donc la couleur de ce dernier ne persiste pas (la solution reste incolore). Après l’équivalence, comme il n’y a plus de $*\ce{H2O2}*$, les ions $*\ce{MnO4^-}*$ versés ne réagissent plus, et donc la solution dans le bécher commence à se colorer. L’équivalence est atteinte dès que la coloration violette persiste.
4. À l’équivalence, on a la relation : $µ \frac{C_1V_1}5 = \frac{C_2V_{2E}}2 µ$ On trouve que $*C_1*$ = 7,9 mmol·L-1
Titrage du dioxyde de soufre
On réalise le titrage d’un volume $*V_1*$ = 15 mL de solution de dioxyde de soufre par une solution de diiode de concentration $*C_2*$ = 2,5 mmol·L-1. Le volume à l’équivalence vaut $*V_{2E}*$ = 18,3 mL.
Données
- Couples rédox : $*\ce{SO4^2-/SO2}*$ et $*\ce{I2/I–}*$
- La seule espèce colorée est le diiode, mais sa coloration est très faible. En présence d’un indicateur coloré appelé Iodex, le diiode prend une coloration bleu foncé très intense.
1. Donner la réaction de titrage.
2. Que faut-il faire pour bien repérer l’équivalence ? Justifier.
3. Calculer la concentration de la solution de $*\ce{SO2}*$.
Correction
1. $*\ce{SO2 + 2 H2O + I2 \rightarrow SO4^2- + 4H^+ + 2I^-}*$
2. Il faut mettre un peu d’iodex dans la solution à doser. Dès qu’on a passé l’équivalence, le $*\ce{I2}*$ introduit ne réagit plus car il n’y a plus de $*\ce{SO2}*$ et donc, en présence d’iodex, il apparaîtra une coloration bleu. Si on ne met pas d’iodex, lorsqu’on repèrera la couleur de $*\ce{I2}*$ dans la solution; il sera trop tard car comme cette coloration est peu intense, ça veut dire qu’il y en a déjà une certaine quantité et qu’on a dépassé l’équivalence depuis un certain temps.
3. À l’équivalence, on a la relation : $µ C_1V_1 = C_2V_{2E} µ$ donc $*C_1*$ = 3,1 mmol·L-1
Titrage indirect de l’eau de Javel
L’eau de Javel contient des ions hypochlorite $*\ce{C\ell O^–}*$ qui ont un caractère oxydant. Le dosage des ions hypochlorite se fait en deux étapes.
1e étape : on verse d’abord dans l’eau de Javel une solution contenant des ions iodures en excès. Il se forme du diiode, mais la réaction est lente et donc ne peut pas être utilisée comme réaction de titrage.
2e étape : on dose ensuite le diiode formé par des ions thiosulfate $*\ce{S2O3^2–}*$. On en déduit ensuite la quantité d’hypochlorite qui a réagi pour former le diiode titré.
Cet exercice s’intéresse à la réalisation du titrage indirect des ions hypochlorite dans une eau de javel.
Données
- L’eau de Javel dosée est supposée contenir des ions hypochlorite à une concentration $*C_0*$ ≈ 0,5 à 0,6 mol·L-1.
- Couples rédox : $*\ce{C\ell O^–/C\ell^–}*$ ; $*\ce{I2/I^–}*$ ; $*\ce{S4O6^2–/S2O3^2-}*$
- La seule espèce colorée est le diiode, qui a une couleur orange-brun. En présence d’un indicateur coloré appelé Iodex, le diiode prend une coloration bleu foncé très intense.
Remarque : il est recommandé de schématiser l’énoncé afin de bien faire le lien entre les différentes étapes.
Questions
L’eau de Javel du commerce est très concentrée. On réalise donc d’abord 50,0 mL d’une solution d’eau de Javel diluée au 10e notée S.
1. Donner le protocole permettant de réaliser cette solution.
Dans un bécher, on introduit $*V_0*$ = 10,0 mL de S puis $*V_1*$ = 10 mL d’une solution d’iodure de potassium ($*\ce{K^+ + I^–}*$) acidifiée (c’est-_à-dire contenant des ions $*\ce{H+}*$) de concentration $*C_1*$ = 0,20 mol·L-1.
2.a. Quelle verrerie doit-on utiliser pour introduire les 10,0 mL de S ? Et les 10 mL de solution d’iodure de potassium ?
2.b. Écrire l’équation-bilan de la réaction qui a lieu entre les ions hypochlorite et les ions iodure. Quelle relation a-t-on entre la qdm initiale d’ions hypochlorite et la qdm de $*\ce{I2}*$ produite ?
2.c. Montrer que l’on a bien introduit les ions $*\ce{I^–}*$ en excès.
2.d. Comment évolue la coloration du mélange ? Justifier.
À la fin de la réaction, on dose la totalité du mélange obtenu avec une solution de thiosulfate de sodium de concentration $*C_2*$ = 0,10 mol·L-1. Le volume à l’équivalence vaut alors $*V_{2E}*$ = 10,9 mL.
3.a. Faire le schéma du titrage.
3.b. Écrire la réaction de titrage.
3.c. Déterminer la quantité de matière de diiode formée.
3.d. En déduire la concentration de S en ions hypochlorite, puis celle de l’eau de Javel. Le résultat est-il compatible avec la valeur attendue ?
Correction
1. Prélever 5,0 mL d’eau de Javel avec une pipette jaugée.
Verser ce volume dans une fiole jaugée de 50 mL.
Compléter avec de l’eau distillée jusqu’au trait de jauge.
Boucher, agiter.
2.a. $*V_0*$ doit être connu très précisément car on souhaite connaître la concentration de l’eau de Javel. Par contre, les ions iodure sont introduits en excès. Ce qui nous intéresse pour la suite, c’est la qdm d’ions iodure qui a réagi, par la qdm qui reste. Donc on n’a pas besoin de connaître ce volume très précisément. On peut donc utiliser une éprouvette graduée.
2.b. $*\ce{C\ell O^- + 2 I^- + 2 H^+ \rightarrow Cl^- + I2 + H2O}*$
Il y a autant de $*\ce{I2}*$ produit qu’il y avait d’ions $*\ce{C\ell O^-}*$ au départ
2.c. La concentration attendue de S en ions $*\ce{C\ell O^-}*$ est d’environ 0,05 à 0,06 mmol·L-1. Donc dans les 10 mL de S, on s’attend à avoir au maximum 0,06×10 = 0,6 mmol de $*\ce{C\ell O^-}*$.
Or on a introduit 10×0,2 = 2 mmol de $*\ce{I^-}*$ alors qu’il en faudrait seulement 2×0,6 = 1,2 mmol pour être en proportion stœchiométrique. On a donc bien introduit les ions $*\ce{I^-}*$ en excès.
2.d. À mesure que la réaction avance, du $*\ce{I2}*$ se forme donc la solution se colore en orange.
3.a. Schéma du montage
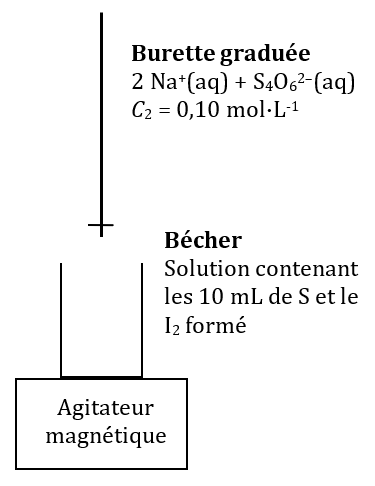
3.b. Équation de la réaction : $µ\ce{I2 + 2 S2O3^2- \rightarrow 2I^- + S4O6^2-}µ$
3.c. À l’équivalence : $µ n(\ce{I2}) = \frac{C_2V_{2E}}2 µ$ on trouve $* n(\ce{I2}) *$ = 0,545 mmol
3.d. On a dit un peu plus haut que $* n(\ce{I2})_f *$ = $* n(\ce{C\ell O^-})_i *$ ce qui signifie qu’il y avait 0,545 mmol de $*\ce{C\ell O^-}*$ dans les 10 mL de S qu’on a dosé. Donc la concentration de $*\ce{C\ell O^-}*$ est de 0,545÷10 = 0,0545 mol·L-1. L’eau de Javel est 10 fois plus concentrée, donc sa concentration est de 0,545 mol·L-1. On s’attendait à une valeur comprise entre 0,5 et 0,6 mol·L-1, ce résultat est bien compatible avec la valeur attendue.