P2. Statique des fluides
Pression et force pressante
- Exploiter la relation $* F = P·S*$ pour déterminer la force pressante exercée par un fluide sur une surface plane $*S*$ soumise à la pression $*P*$.
- Utiliser la loi de Mariotte.
En physique, un fluide, c’est un liquide ou un gaz. Un fluide exerce, sur toute surface avec laquelle il est en contact, une force pressante perpendiculaire à cette surface. Cette force est une poussée : elle est orientée du fluide vers la surface. En d’autres termes, le fluide « appuie » sur la surface. Il ne « tire » pas dessus.
Pression d’un fluide
La pression d’un fluide, c’est la force qu’il exerce par unité de surface. En d’autres termes, c’est le nombre de newtons que la force de « poussée » du fluide exerce sur chaque m2 de cette surface.
| $µ P=\frac FS µ$ | $*P*$ : pression (pascal, Pa) $*F*$ : force exercée sur la surface (newton, N) $*S*$ : surface (m2) |
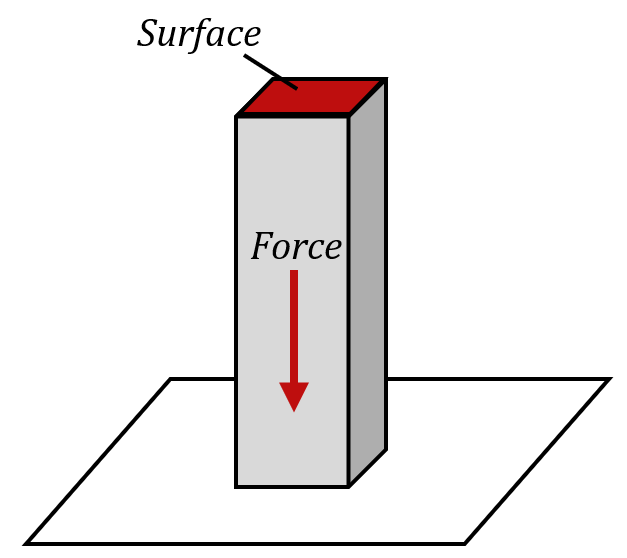
1 Pa = 1 N·m-2. C’est une pression très faible par rapport à la pression atmosphérique au niveau de la mer (105 Pa).
Comme le pascal est une unité très petite par rapport aux pressions qu’on peut rencontrer au quotidien, on utilise souvent, en météo, l’hectopascal hPa (1 hPa = 100 Pa).
Pour exprimer des pressions plus élevée, on utilise souvent le bar (1 bar = 105 Pa) ou l’atmosphère (1 atm = 1,013·105 Pa $* \simeq *$ 1 bar).
Mais attention, dès que vous utilisez la formule $*P=F/S*$, vous devez utiliser les unités S.I. et donc le pascal pour la pression.
Pression atmosphérique
1. Calculer la force que l’atmosphère exerce sur une fenêtre de 1 m2. Comparer cette force au poids d’un éléphant (environ 3 tonnes). Pourquoi la fenêtre ne se brise-t-elle pas ?
2.a. Expliquer pourquoi les hublots d’avion sont petits et constitués de verre épais.
2.b. La pression à l’intérieur de l’avion est égale à 80 % de la pression atmosphérique au niveau de la mer. À 10 km d’altitude, la pression atmosphérique n’est plus que de 265 hPa. Sachant que la surface d’un hublot est de 600 cm2, calculer la force à laquelle le hublot doit résister.
Correction
1. $*F = P·S = *$ 105 N. Poids d’un éléphant : 3·104 N. La force exercée sur la fenêtre par la pression atmosphérique est supérieure au poids d’un éléphant. La fenêtre ne se brise pas car cette force s’exerce des deux côtés de la fenêtre (il y a de l’air des deux côtés).
2.a. La pression à l’intérieur de l’avion est plus élevée qu’à l’extérieur lorsqu’il vole à haute altitude.
Donc dans cette situation la force exercée par l’air à l’intérieur de l’avion est supérieur à celle exercée par l’air à l’extérieur.
Le hublot est petit pour minimiser cette force, puisqu’elle dépend de $*S*$. Et le verre doit être épais pour résister à la différence de pression.
2.b. À l’intérieur, $*F_{int}*$ = 0,8·105×0,06 = 4,8 kN.
À l’extérieur, $*F_{ext}*$ = 265·102×0,06 = 1,6 kN.
Le hublot doit résister à la différence de ces forces, soit 3,2 kN
Loi de Mariotte

TP Loi de Mariotte
- Tester la loi de Mariotte, par exemple en utilisant un dispositif comportant un microcontrôleur.
- Mesurer une pression dans un gaz et dans un liquide.
Loi de Mariotte
En 1676, l’abbé Edme Mariotte publie un livre dont le titre est « De la nature de l’air », où il présente une loi qui porte désormais son nom.
Cette loi s’énonce ainsi :
Lorsque l’on diminue le volume $*V*$ occupé par un gaz, à température constante, sa pression $*P*$ augmente selon la relation :
$*P×V*$ = constante
Objectif du TP : vérifier expérimentalement cette loi.
Expérience n°1 : première approche

Débrouillez-vous avec le matériel dont vous disposez pour réaliser une première expérience.
Cette première vérification vous satisfait-elle ?
Comment pourrait-on expliquer l’écart entre le résultats des mesures et les valeurs attendues ?
Expérience n°2 : soyons plus précis
Refaite l’expérience en tenant compte des améliorations proposées après votre première expérience.
Cette deuxième expérience fournit-elle des résultats plus en adéquation avec la loi de Mariotte ?
Éléments de réponses
Pour obtenir une précision satisfaisante, il faut tenir compte du volume d’air dans le tuyau reliant la seringue au pressiomètre, ainsi que l’air contenu dans le pressiomètre.
Pour estimer ce volume d’air, on place le piston de la seringue à 0, à la pression atmosphérique. Puis on tire sur le piston jusqu’à ce que la pression indiquée soit la moitié de la pression atmoshpérique. Le volume lu sur la seringue correspond au volume d’air présent dans le tuyau et dans le pressiomètre.
On mesure ensuite la pression mesurée pour différents volumes d’une même quantité d’air. On trace le graphique $*P = f(V)*$, puis on modélise ce graphique par une fonction puissance. La puissance de $*V*$ calculée par Excel est très proche de -1, qui est la valeur attendue d’après la loi de Mariotte.
Les résultats expérimentaux sont réunis dans ce fichier Excel.
Pour une quantité de gaz constante, à température constante :
| $*P·V*$ = constante | $*P*$ : pression du gaz $*V*$ : volume |
La constante dépend des unités utilisées, de la température du gaz et de la qdm de gaz.
Cette loi n’est valide que pour des pressions pas trop élevées (inférieure à 107 Pa pour la plupart des gaz).
Application de la loi de Mariotte
1. Un bouteille de plongée moyenne a un volume de 12 L. L’air y est stocké à une pression de 200 bars. À quel volume d’air cela correspond-il à pression atmosphérique ?
2. La ventilation de l’Homme lors d’un effort modéré est d’environ 20 litres d’air par minute. La bouteille de plongée lui fournit de l’air à la même pression que la pression environnante. Quelle est l’autonomie apportée par la bouteille s’il reste en surface (pression de 1 bar) ? Quelle est son autonomie à 20 m de profondeur, où règne une pression de 3 bars ?
Correction
1. Lors de sa mise en bouteille, la pression de l’air a été multipliée par 200. Donc son volume a été divisé par 200. Donc le volume d’air à pression atmosphérique est de 12×200 = 2400 L
2. À la surface, 2400÷20 = 120 minutes.
À 20 m, le volume d’air n’est plus que de 800 L, donc l’autonomie est de 800÷20 = 40 minutes.
Description d’un fluide
- Expliquer qualitativement le lien entre les grandeurs macroscopiques de description d’un fluide et le comportement microscopique des entités qui le constituent.
Fluide à l’échelle microscopique
Une série de belles animations interactives à voir absolument.
Liquide
Dans un liquide, les particules qui le composent (des molécules la plupart du temps, mais ça peut aussi être des atomes individuels si on parle d’un métal en fusion, ou d’un gaz noble à l’état liquide, ou même des ions – les solides ioniques peuvent fondre à des températures relativement élevées) se déplacent les unes par rapport aux autres tout en restant en contact ou quasiment en contact. Elles glissent sans cesse les unes sur les autres à cause de l’agitation thermique.
Gaz
Les particules sont très espacées et entourées de vide. Elles se déplacent en ligne droite et ne changent de direction qu’après un choc avec d’autres particules ou avec un obstacle. Les interactions entre entités sont très faibles (considérée comme nulle dans le modèle des gaz « parfaits »).
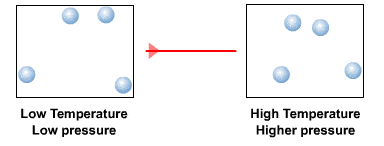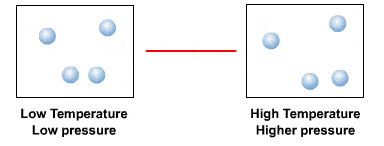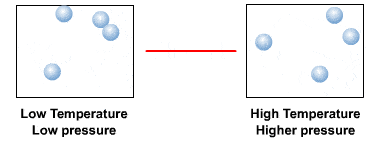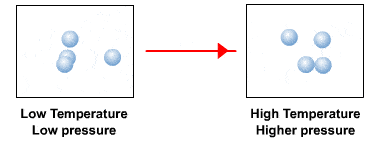
Température
La température, c’est une grandeur macroscopique. C’est-à-dire que c’est une grandeur qu’on peut percevoir et mesurer à notre échelle. Mais à l’échelle des atomes et des molécules, la température « n’existe pas ». 😮
En fait, la température, ça correspond à l’échelle microscopique, à l’agitation des particules. Plus précisément, la température d’un échantillon de matière est proportionnelle à l’énergie cinétique moyenne des particules qui la composent.
Au « zéro abolu », c’est-à-dire à 0 kelvin (K), soit -273,15 °C, les particules sont totalement immobiles. Et plus la température d’un échantillon de matière est élevée, plus la vitesse de ses particules est élevée.
Pression
Comme pour la température, la pression d’un fluide est une grandeur macroscopique. La pression d’un fluide est due aux chocs des particules contre une surface donnée. Plus les chocs sont fréquents et plus ils sont violents, plus la pression du fluide est élevée.
Loi fondamentale de l’hydrostatique
- Dans le cas d’un fluide incompressible au repos, utiliser la loi fondamentale de l’hydrostatique : $*P_2 - P_1 = \rho g(z_1 - z_2)*$.
TP Loi fondamentale de l’hydrostatique
- Tester la loi fondamentale de la statique des fluides..

Quand nous plongeons en piscine ou en mer, nous savons d’expérience que nos oreilles deviennent douloureuses au cours de la descente : la pression de l’eau devient supérieure à celle de l’air contenu dans l’oreille moyenne et déforme notre tympan.
Problématique du TP : quelle relation entre la profondeur d’une étendue d’eau et la pression qui y règne ?
Travail à faire
Répondre à la problématique du TP. 😊
Matériel disponible
- Un pressiomètre
- Petit matériel du laboratoire
Bonus
Si le temps le permet, vous pouvez refaire l’expérience avec de l’éthanol plutôt que de l’eau, pour observer l’influence de la masse volumique du fluide sur la pression. La densité de l’étanol à 96° est de 0,81
Un liquide est un fluide incompressible (rappelez-vous la description microscopique : dans un liquide, les particules sont en contact les unes avec les autres, donc il n’y a aucun « espace vide » qui pourrait être réduit – et les atomes sont incompressibles, sauf cas extrêmes qui ne se produisent pas sur Terre).
Dans un liquide, la pression $*P*$ (en Pa) à une profondeur $*h*$ (en m) suit la loi fondamentale de l’hydrostatique :
| $*P = \rho gh + P_0*$ | $*\rho*$ : masse volumique du fluide (kg·m-3) $*h*$ : profondeur (m) $*g*$ : intensité de la pesanteur (N·kg-1) $*P_0*$ : pression à la surface du liquide (Pa) |
Application à l’eau
La loi fondamentale de la statique des fluides appliquée à une étendue d’eau au niveau de la mer devient, avec $*\rho*$ = 1000 kg·m-3, $*g \simeq*$ 10 N·kg-1 et $*P_0 \simeq*$ 105 Pa : $µ P \simeq 10^4×h + 10^5 µ$
Avec $*P*$ en pascals. Ça peut être intéressant de retenir le résultat approximatif suivant : chaque fois qu’on descend de 10 m, la pression augmente d’une atmosphère.
Pression et profondeur
1. Quelle pression règne-t-il au fond de la fosse des Mariannes (11 km de profondeur) ? Exprimer cette pression en bar (1 bar = 105 Pa)
2. Un sous-marin nucléaire peut descendre à environ 400 m de profondeur. À quelle pression doit-il résister ?
Correction
1. $*P = 10^4×11·10^3 + 10^5 \simeq 11·10^7*$ Pa, soit environ 1100 bar.
2. $*P = 10^4×400 + 10^5 = 41·10^5*$ Pa.
Et en hauteur, ça marche aussi ?
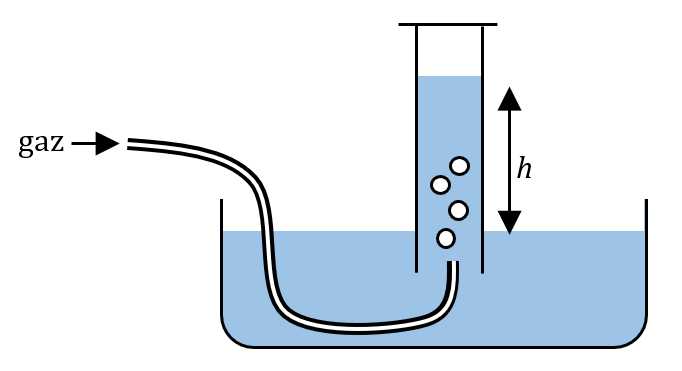
Dans la technique de récupération d’un gaz dite « par déplacement d’eau », on recueille un gaz dans une éprouvette graduée préalablement remplie d’eau et retournée dans un récipient remplie d’eau également. Cette technique permet de mesurer le volume du gaz dégagé et donc sa quantité de matière.
1. Exprimer la pression $*P_e*$ du gaz dans l’éprouvette en fonction de $*h*$. Cette pression est-elle plus grande ou plus petite que la pression atmosphérique ?
2.a. Sachant que le volume molaire d’un gaz vaut $*V_{M0}*$ = 24 L·mol-1 à la pression atmosphérique, calculer le volume molaire $*V_{Me}*$ d’un gaz dans l’éprouvette pour $*h*$ = 20 cm.
2.b. Calculer l’écart relatif entre ces deux volumes molaires.
Correction
1. Dans un fluide statique (c’est-à-dire où il n’y a pas de mouvement interne), tous les points se trouvant sur une même surface horizontale sont à la même pression. Ça signifie que tous les points situés sur la ligne en pointillé rouge sont à la même pression, qui est la pression atmosphérique $*P_0*$.
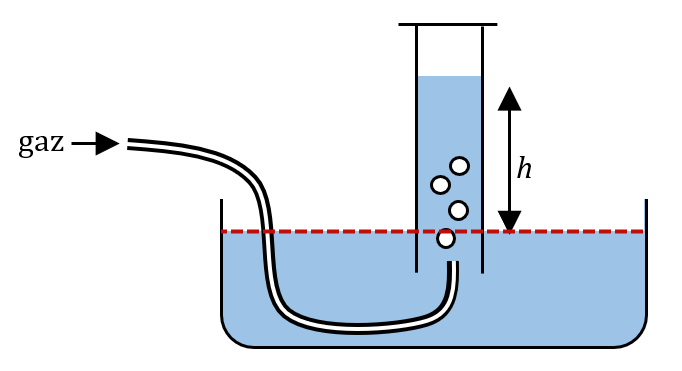
La pression dans l’eau contenue dans l’éprouvette à la profondeur $*h*$ vaut $*P = \rho g h + P_e*$.
Au niveau de la ligne rouge dans l’éprouvette, on peut écrire : $*P_0 = \rho g h + P_e*$. Soit : $* P_e = P_0 - \rho g h *$
On voit que $* P_e \lt P_0 *$
2.a. Pour $*h*$ = 20 cm, on a $*P_e = 10^5 - 10^4×0,2 = 0,98·10^5*$ Pa
D’après la loi de Mariotte, on peut écrire que $*P_0V_{M0} = P_eV_{Me}*$, d’où :
$µ V_{Me} = \frac{P_0}{P_e}V_{M0} \simeq 24,5 \;\text{L·mol}^{-1} µ$
2.b. $*V_{Me}/V_{M0}*$ = 1,02. $*V_{Me}*$ est environ 2 % plus grand que $*V_0*$.
Océan de Mare Infinitus
Imaginons une planète océan d’un diamètre de 3000 km, d’une densité égale à celle de la Terre (5,5) et d’une pression atmosphérique égale à 0,4 atmosphère.

Correction
La relation $*P = \rho_{\text{eau}} g h + P_0*$ est toujours applicable, mais il faut utiliser l’intensité de la pesanteur $*g*$ de cette planète (et donc la calculer), ainsi que la pression $*P_0*$ à la surface de l’océan de cette planète (0,4×105 Pa).
On a vu au cours du chapitre P1 que :
$µ g = \frac{GM}{r^2} µ$
$*r*$ est la rayon de la planète (ici, 1500 km) et $*M*$ est la masse de la planète.
$*M = \rho_{\text{planète}} V*$, avec $*\rho*$ qui vaut 5,5·103 kg·m-3, donc :
$µ
\begin{aligned}
g &= \frac{G \rho \frac 43 \pi r^3}{r^2} \\
g &= G \rho \frac 43 \pi r
\end{aligned}
µ$
D’où $*g*$ = 2,30 N·kg-1.
Donc l’expression numérique liant $*P*$ en Pa à la profondeur $*h*$ en mètres est : $*P = 2300×h + 4·10^4*$
Révision & entraînement
Pont hydraulique
Un pont élévateur hydraulique permet de soulever des voitures dans un garage. Il est composé d’un piston sur lequel s’exerce une pression $*P_1*$ générée par un compresseur.
Le piston presse sur un fluide incompressible en contact avec le pont élévateur de surface $*S*$ = 1,0 m2.
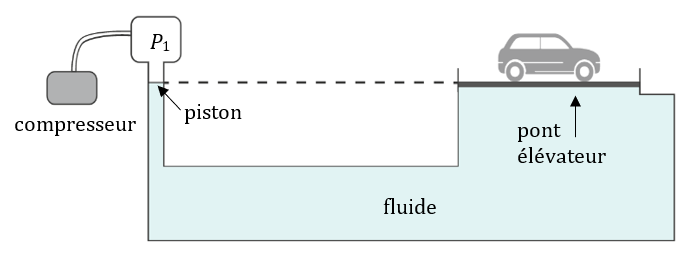
Données : 1 bar = 105 Pa ; intensité de la pesanteur $*g \simeq*$ 10 N·kg-1.
1. Lorsque le piston et le pont élévateur se situent à la même hauteur, comme indiqué sur le schéma, quelle est la pression que le fluide exerce sur le pont élévateur ? Justifier.
2. Le compresseur applique une pression $*P_1*$ = 1,2 bar sur le piston. Calculer la force exercée par le fluide sur le pont élévateur.
3. Cette force est-elle capable de soulever une voiture dont la masse est $*m*$ = 1,3 t ?
Remarque : pour soulever la voiture, il faut que la force exercée par le fluide soit supérieure à la somme de la force exercée par l’atmosphère sur le pont et au poids de la voiture.
Correction
1. La pression dans un fluide ne dépend que de la profondeur. Donc si le piston et le pont élévateur sont au même niveau, la pression du fluide en contact avec le piston est égale à la pression du fluide en contact avec le pont élévateur, c’est-à-dire $*P_1*$.
2. $*F = P_1×S =*$ 1,2·105 N
3. Force exercée par la pression atmosphérique $*P_0*$ : $*F_{atm} = P_0×S = *$ 105 N
Poids de la voiture : $*P = mg =*$ 0,13·105 N
On constate que 1,2·105 > 1,13·105, donc cette pression est suffisante pour soulever la voiture.
Plongée en fosse
Cet exercice a été donné en devoir en 2020/2021 et est un sujet d’E3C.
Un plongeur descend progressivement au fond d’une fosse de plongée. Cette fosse est composée d’une colonne d’eau de 20 mètres de profondeur et de 6 m de diamètre.
Données
- Pression atmosphérique : $*P_0*$ = 1,013·105 Pa
- Masse volumique de l’eau : $*\rho*$ = 1,0·103 kg·m-3
- Intensité du champ de pesanteur : $*g*$ = 9,81 N·kg-1
1. Pression à une profondeur donnée
La loi fondamentale de la statique des fluides précise que pour un fluide au repos incompressible de masse volumique $*\rho*$, la différence de pression entre deux points, A et B, s’exprime par la relation : $µ P_A-P_B=\rho g(z_B-z_A) µ$
Les altitudes z_A et z_B sont repérées sur un axe vertical ascendant $*\mathrm{O}z*$.
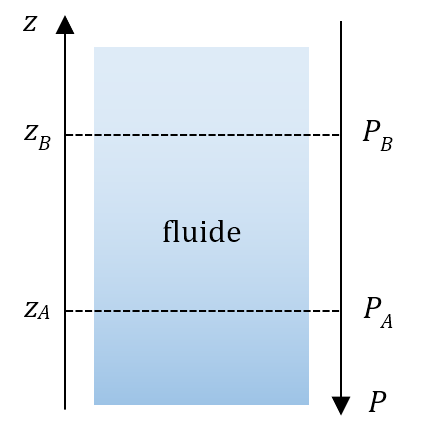
1.1. Montrer, à l’aide de la relation de la statique des fluides, qu’à 20 m de profondeur, la pression vaut environ 3 fois la pression atmosphérique.
On veut vérifier expérimentalement la loi fondamentale de la statique des fluides. Pour cela, on réalise une série de mesures de la pression $*P*$ au sein d’une éprouvette graduée contenant de l’eau, en fonction de la profondeur $*h*$.
Les valeurs mesurées permettent de représenter le graphe P en fonction de h à l’aide d’un tableur. On obtient alors une droite modélisée par l’équation mathématique suivante :
$*P*$ = 9,771·103×$*h*$ + 101,3·103
$*P*$ est exprimée en Pa et $*h*$ en m.
1.2. Que représente la valeur de la pression $*P_0*$ à la profondeur $*h*$ = 0 m ?
1.3. Expliquer pourquoi les mesures expérimentales sont compatibles avec la loi fondamentale de la statique des fluides.
2. Autonomie d’un plongeur
Lors de la plongée en bouteille le détendeur permet au plongeur de respirer de l’air à la même pression que la pression à la profondeur où il se trouve.
2.1. On note $*V_1*$ le volume d’air disponible dans la bouteille de plongée lorsqu’elle est mise sous pression à la pression $*P_1*$ et $*V_2*$ celui d’air disponible pour le plongeur lorsque qu’il est à la pression $*P_2*$. Les températures sont supposées identiques dans les deux situations.
Donner la relation liant $*V_1*$, $*P_1*$, $*V_2*$ et $*P_2*$.
2.2. En supposant que la consommation en volume d’air du plongeur reste toujours la même au cours de la plongée, expliquer sans calcul comment l’autonomie en air du plongeur évolue avec la profondeur.
2.3. Le plongeur dispose d’une bouteille de plongée d’une capacité de 12 litres mise sous pression à la pression initiale de 200 bars. Calculer la durée durant laquelle le plongeur peut rester à 20 m de profondeur sachant qu’il consomme 15 litres d’air par minute.
3. La manœuvre de Valsalva
En plongée, la différence de pression de part et d’autre du tympan peut provoquer une vive douleur. La manœuvre de Valsalva consiste à souffler par le nez, bouche fermée et nez pincé afin de faire pénétrer de l’air dans l’oreille moyenne. L’air extérieur passe par la trompe d’Eustache.
3.1. Calculer la valeur de la force pressante $*F_1*$ exercée par l’air emprisonné dans l’oreille moyenne à la pression de 105 Pa sur la paroi interne du tympan dont la surface est de 70 mm².
3.2. La valeur de la force pressante $*F_2*$ exercée par l’eau sur la paroi externe du tympan pour un plongeur situé à 20 m de profondeur est de 21 N.
Compléter le schéma ci-dessous, en représentant les forces pressantes $*\vec{F}_1*$ et $*\vec{F}_2*$ exercées sur le tympan (échelle : 1 cm pour 7 N).
En déduire pourquoi le plongeur ressent une vive douleur lors de la descente.
3.3. Expliquer pourquoi la manœuvre de Valsalva permet de compenser la pression de l’eau introduite dans le conduit auditif.
Correction
1.1. On prend $*z_A*$ = –20 m et $*z_B*$ = 0.
$*P_B*$ = $*P_0*$ ≃ 105 Pa
$*P_A*$ = $*ρg*$×20 + $*P_0*$ ≃ 103×10×20 + 105 = 3×105 Pa, c’est-à-dire 3 fois la pression atmosphérique.
1.2. $*P_0*$ est la pression atmosphérique.
1.3. La loi fondamentale de l’hydrostatique donne $*P*$ = $*ρgh + P_0 *$ = 9,8·103·$*h*$ + 1,013·105.
Ces deux relations sont très proches
2.1. $*P_1 V_1=P_2 V_2*$
2.2. Si la profondeur augmente, la pression augmente donc le volume d’air disponible diminue.
2.3. À 20 m, la pression vaut 3 bar. Donc $*V_2*$ = 12×200÷3 = 800 L.
À raison de 15 L/min, le plongeur a une autonomie de 800÷15 = 53 minutes environ.
3.1. $*F_1=P·S =*$ 105 × 70·10-6 = 7 N
3.2. Schéma des forces pressantes :
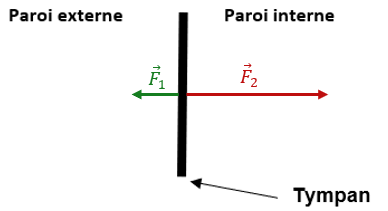
La force pressente sur la paroi externe est trois fois supérieure à la force pressante sur la paroi interne. Cela provoque une déformation douloureuse.
3.3. Cette manœuvre permet d’introduire de l’air dans l’oreille moyenne et donc d’augmenter la pression interne, pour compenser la pression externe.
Liquides dans un tube en U
Soit un tube en U rempli partiellement de mercure. On ajoute un volume d’eau d’un côté du tube, sur une hauteur $*h_2*$ de 15 cm.
L’eau et le mercure sont non miscibles.
La densité du mercure (Hg) vaut d = 13,55.
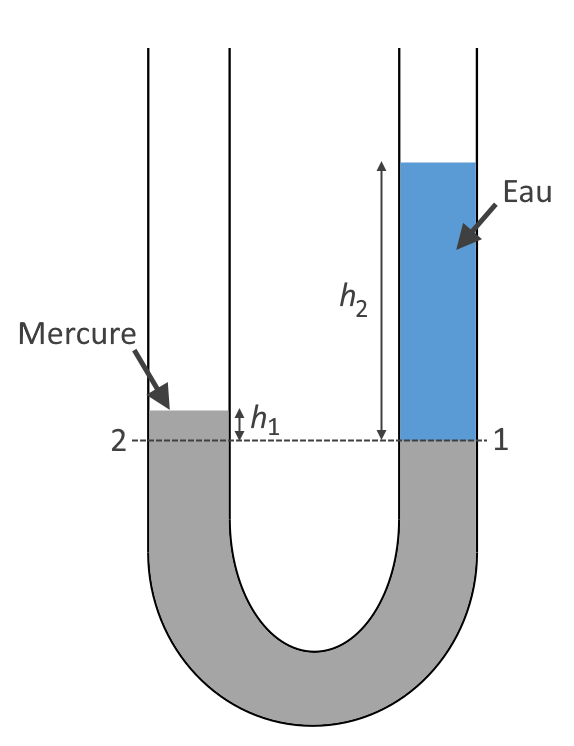
1. Exprimer la pression dans le mercure à la profondeur $*h_1*$. Faites de même pour l’eau à une profondeur $*h_2*$
2. Exprimer $*h_1*$ en fonction de $*h_2*$ et d’autres grandeurs pertinentes, en remarquant que la pression au niveau 1 et la même que celle au niveau 2.
Soit un tube en U fermé à l’une de ses extrémités. Ce tube contient de l’eau et de l’air à la pression $*P_1*$ dans sa partie fermée. La partie ouverte est à la pression atmosphérique $*P_0*$.
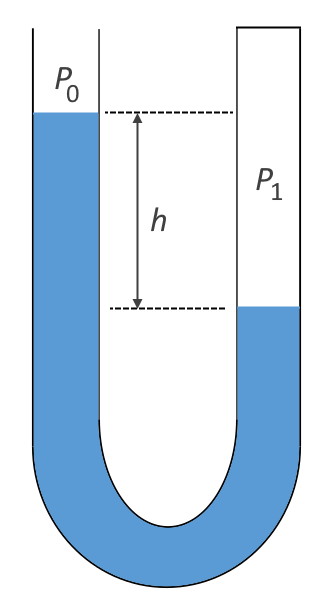
3. Exprimer la différence de hauteur $*h*$ entre les surfaces libres de l’eau des deux côtés du tube en fonction de $*P_0*$ et $*P_1*$.
Correction
1. Dans le mercure : $*P_1 = \rho_{\ce{Hg}}·g·h_1 + P_0*$
Dans l’eau : $*P_2 = \rho_{\mathrm{eau}}·g·h_2 + P_0*$
2. Comme $*P_1 = P_2*$, on a : $µ \rho_{\ce{Hg}}·g·h_1 + P_0 = \rho_{\mathrm{eau}}·g·h_2 + P_0 µ$ Après simplification par $*P_0*$ puis par $*g*$, on obtient : $µ \rho_{\ce{Hg}}·h_1 = \rho_{\mathrm{eau}}·h_2 µ$ Et donc : $µ h_1 = \dfrac{\rho_{\mathrm{eau}}·h_2}{\rho_{\ce{Hg}}} µ$
3. À la profondeur $*h*$ dans le côté du tube exposé à la pression atmosphérique, la pression est égale à $*P_1*$.
Donc on peut écrire : $* P_1 = \rho g h + P_0 *$
D’où $*h = \dfrac{P_1 - P_0}{\rho g} *$