P4. Énergie électrique

L’énergie électrique est omniprésente dans notre entourage. Ce chapitre vous présente quelques notions de base.

Courant continu

Relier intensité d’un courant continu et débit de charges.

Courant électrique : un courant électrique, c’est tout simplement un déplacement de charges électriques. Dans un métal, il s’agit d’un déplacement d’électrons (appelés électrons de conduction). Dans une solution ionique, les porteurs de charge sont les ions positifs et négatifs.

Courant électrique continu : courant électrique dont l’intensité ne varie pas au cours du temps.

Rappel : par convention, le courant se déplace du pôle + au pôle – .

Intensité d’un courant continu

Un courant de 1 A (ampère) qui circule dans un conducteur correspond à une charge électrique de 1 C (coulomb) qui traverse une section du conducteur à chaque seconde. Autrement dit, 1 A = 1 C·s^-1.

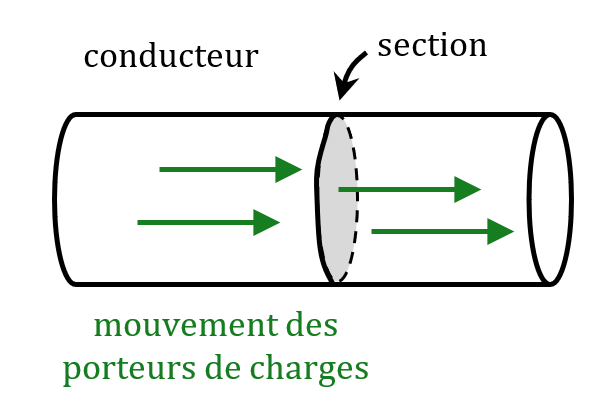
Courant et porteurs de charge

1. Quelle qdm d’électrons doit traverser la section d’un fil électrique chaque seconde pour obtenir un courant de 1,0 A ?

2. À quelle intensité correspond le débit d’un milliard d’électrons par milliseconde ?

Données
• charge de l’électrons $*-e*$ = –1,60·10^-19 C
• nombre d’Avogadro $*N_A*$ = 6,02·10²³ mol^-1.

Correction

1. 1 A = 1 C·s^-1. Il faut donc calculer combien d’électrons sont nécessaires pour obtenir une charge de 1,0 C, puis calculer la qdm que cela représente.
Nombre d’électrons : 1÷1,60·10^-19 = 6,25·10¹⁸ électrons
Qdm d’électrons : 6,25·10¹⁸÷6,02·10²³ = 1,04·10^-5 mol

2. 10⁹ électrons par milliseconde = 10¹² électrons par seconde.
Charge de 10¹² électrons : 1,60·10^-7 A (0,16 µA !)

Générateur de tension continue

Expliquer quelques conséquences pratiques de la présence d’une résistance dans le modèle d’une source réelle de tension continue.

Rappel : loi d’Ohm

Dans un conducteur ohmique, l’intensité du courant est proportionnelle à la tension à ses bornes

$µ U = R·I µ$

$*U*$ : tension aux bornes du conducteur (V)
$*R*$ : résistance électrique (Ω)
$*I*$ : intensité du courant qui traverse le conducteur (A)

Exemples de conducteurs ohmiques : résistance, fil électrique.

Exemples de conducteurs non ohmiques (qui ne respectent pas la loi d’Ohm) : moteur électrique, diode.

Modèle du générateur idéal de tension

Lorsque, au collège, vous avez étudié des circuits électriques, vous avez toujours considéré que la tension aux bornes du générateur était constante.

Il s’agit d’une modélisation d’un générateur qui considère que la tension fournie par le générateur est totalement indépendant de l’intensité du courant qu’il délivre. On appelle ça le modèle du générateur idéal de tension.

Cette modélisation a l’avantage d’être simple et suffit dans beaucoup de situations (toutes celles que vous avez rencontrées au collège). Mais il y a parfois des situations où il faut alors élaborer une modélisation plus fine pour rendre compte de ce qu’il se passe réellement dans un circuit électrique.

Modèle du générateur réel de tension

TP Caractéristique d’un générateur de tension

Déterminer la caractéristique d’une source réelle de tension et l’utiliser pour proposer une modélisation par une source idéale associée à une résistance.

Objectif : tracer la caractéristique d’un générateur réel de tension et en déduire sa résistance interne.

Matériel disponible

Une pile de 4,5 V ; un boîtier de résistance variable ; 2 multimètres ; des fils électriques

Recommandations

Attention à ne jamais dépasser l’intensité maximale admissible par la résistance. Cette intensité dépend de la résistance. Vous vérifierez que vous pouvez utiliser les valeurs de résistance choisies.

Travail demandé

• Mesurer la tension $*U*$ aux bornes de la pile pour différentes valeurs d’intensité $*I*$ variant de 0 à un peu moins de 200 mA.

Utiliser les mesures contenues dans ce fichier.

• Tracer un graphique montrant la loi de fonctionnement $*U = f (I)*$ de la pile

Inutile de faire trop de mesures : une mesure de tension pour $*I*$ = 0 ; 50 ; 100 ; 150 ; et 190 mA est suffisante.

Exploitation

1. Modéliser le graphique obtenu.

2. Associer, à chaque facteur et terme de la modélisation, sa signification physique.

3. Comment expliquer que deux générateurs fournissant une même tension (par exemple, 5V pour un chargeur USB) ne soient pas toujours capables de fournir la même intensité (1000 mA pour un chargeur « standard », 2000 mA pour un chargeur de tablette numérique) ?

Éléments de réponses

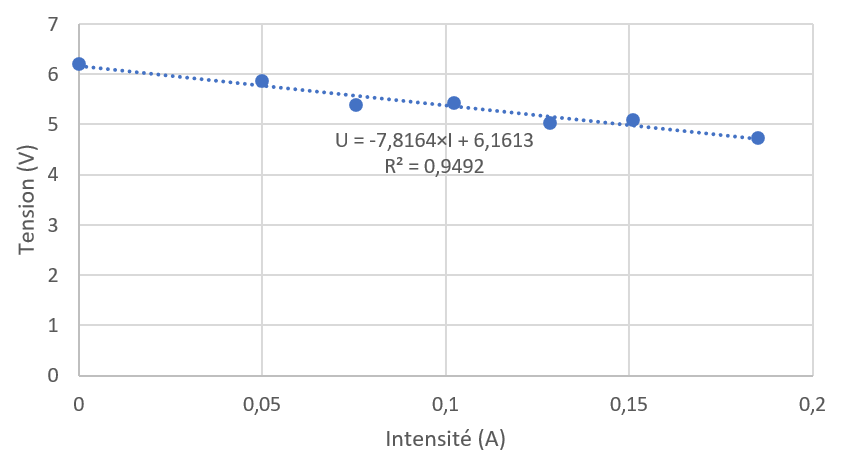
Le coefficient directeur de cette droite (≃ –7,8) est une grandeur telle que, lorsqu’elle est multipliée par une intensité, on obtient une tension. Il s’agit donc d’une résistance. De fait, la résistance interne de la pile est égale à l’opposé de ce coefficient directeur (soit 7,8 Ω).

L’ordonnée à l’origine correspond à la tension aux bornes de la pile lorsque celle-ci ne fournit aucun courant. Cette valeur s’appelle force électromotrice du générateur, ou encore tension à vide.

Un générateur de tension peut être modélisé par l’association en série d’un générateur idéal de tension fournissant une tension $*E*$ à ses bornes ainsi que d’une résistance appelée résistance interne (généralement petite, sauf si le générateur est de mauvaise qualité ou s’il s’agit d’une pile déjà assez usée) notée $*r*$.

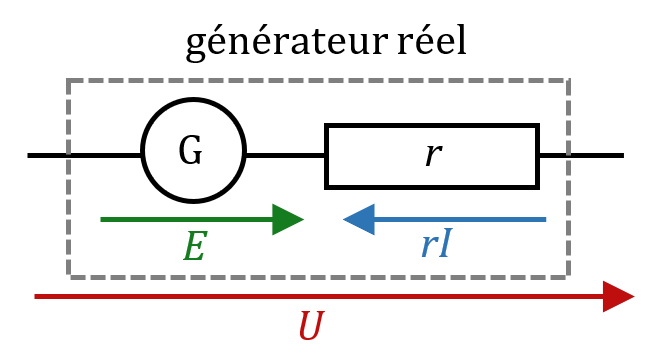
La tension aux bornes d’un générateur de tension de résistance interne $*r*$ est donnée par la relation :

$µ U = E - rI µ$

$*U*$ : tension aux bornes du générateur (V)
$*E*$ : force électromotrice (f.é.m) ou tension à vide (V)
$*r*$ : résistance interne (Ω)
$*I*$ : intensité du courant fourni par le générateur (A)

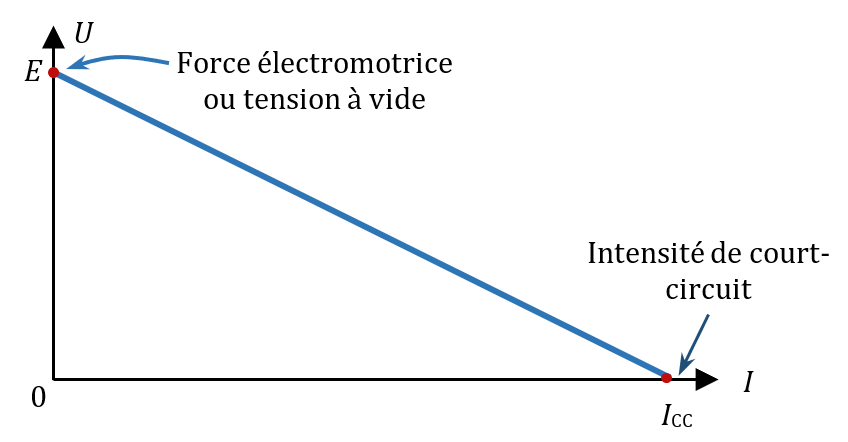
Caractéristique tension – intensité d’un générateur non idéal de tension

Plus la résistance interne aux bornes d’un générateur est élevée, plus sa tension baisse lorsqu’on lui demande du courant. À l’inverse, plus sa résistance interne est faible, plus son comportement se rapproche d’un générateur idéal de tension.

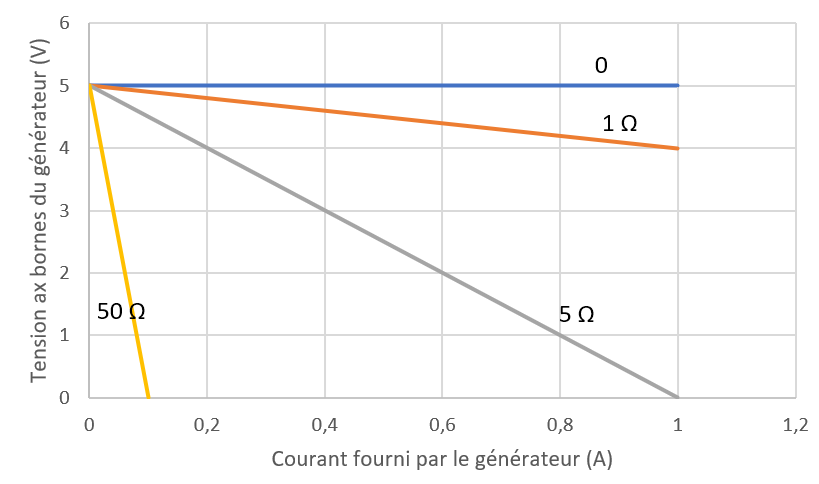
Effet de la résistance interne sur la tension aux bornes d’un générateur

Un générateur qui doit fournir une puissance électrique importante tout en maintenant la tension souhaitée entre ses bornes doit avoir une résistance interne faible (il est donc plus cher et généralement plus gros qu’un générateur de moins bonne qualité…).

Chargeur USB

On considère un chargeur USB, qui est un générateur de tension de force électromotrice $*E*$ = 5,0 V et de résistance interne $*r*$ = 1,2 Ω.

On connecte à ce chargeur un téléphone, que l’on assimilera à un conducteur ohmique de résistance $*R*$ = 5,5 Ω. Celui-ci peut se recharger si la tension aux bornes du chargeur est au moins égale à 4,0 V.

1. Quelle sera l’intensité du courant de charge fourni par le générateur ? Le téléphone peut-il se recharger ?

2. Même question pour le rechargement d’une tablette, assimilée à un conducteur ohmique de résistance $*R*$ = 2,5 Ω. Celle-ci doit également avoir 4,0 V au moins entre ses bornes pour se recharger.

Correction

1. La tension aux bornes du téléphone ($*RI*$) est égale à la tension aux bornes du chargeur ($*E-rI*$), donc : $*RI = E – rI*$ $*\Rightarrow*$ $*I = \frac E{R + r} =*$ 0,75 A.
Tension aux bornes du téléphone : $*U = RI =*$ 5,5×0,75 = 4,1 V.
Le téléphone peut se recharger.

2. Par le même calcul, on obtient $*I*$ = 1,35 A et $*U*$ = 3,4 V.
La tablette ne peut donc pas se recharger.

Puissance et énergie électriques

Citer quelques ordres de grandeur de puissances fournies ou consommées par des dispositifs courants.

✋ Avant toute chose, vous allez lire ce rappel sur Puissance & énergie.

Puissance électrique

La puissance électrique $*P_e*$ fournie par un générateur ou consommée par un récepteur (quelque soit sa nature) vaut :

$µ P_e = U·I µ$

$*U*$ : tension aux bornes du générateur/récepteur (V)
$*I*$ : intensité du courant traversant le générateur/récepteur (A)

Bilan de puissance dans un circuit électrique

L’énergie consommée par les récepteurs électriques est égale à l’énergie fournie par le générateur qui les alimente.

Ordre de grandeur de puissances électriques

Appareil	Puissance	Appareil	Puissance
Lampe LED	4-8 W	Voiture électrique	50-200 kW
Lampe à filament	25-100 W	Panneaux solaires 10 m² (plein soleil)	1,5 kW
Ordinateur portable	15-30 W	Éolienne (100 m)	2-3 MW
Radiateur électrique	1-2 kW	Réacteur nucléaire	800 MW

Puissance électrique

Une alimentation d’ordinateur portable fournit une tension de 19 V et un courant de 1,3 A. Quelle est la puissance électrique fournie ? Quelle est la puissance électrique consommée par l’ordinateur ?

Correction

Puissance électrique fournie : $*P*$ = 19×1,3 = 24,7 W
Puissance électrique consommée : c’est la même !

Consommation domestique d’énergie électrique

Sur les factures d’électricité, l’énergie consommée est exprimée en kilowatt-heure (kW·h). 1 kW·h est l’énergie consommée par un récepteur électrique d’une puissance de 1 kW pendant une durée d’une heure.

1. Convertir 1 kWh en unité S.I de l’énergie.

2. Deux personnes dans un appartement de 80 m² consomme 250 kW·h par mois (hors chauffage) en faisant attention à leur consommation. Quelle part de la facture énergétique mensuelle représentent…

Une veilleuse de télévision de 0,5 W fonctionnant en permanence.
Un éclairage extérieur de 200 W fonctionnant chaque nuit pendant 10 h.
L’économie d’énergie réalisée par le remplacement de 10 ampoules à filament de 50 W par 10 ampoules à LED d’une luminosité équivalente consommant 8 W. Elles fonctionnent 4h / jour.
Deux plaques de cuisson de 1000 W chacune fonctionnant 30 minutes tous les jours.

Correction

1. 1 kWh : $*E*$ = 1 kW×3600 s = 3600 kJ = 3,6 MJ.

2.a. $*E*$ = 1,30·10⁶ J soit 0,14 %
2.b. $*E*$ = 2,16·10⁸ J soit 24 %
2.c. $*E*$ = 1,81·10⁸ J soit 20 %
2.d. $*E*$ = 1,08·10⁸ J soit 12 %

Effet Joule

La puissance électrique reçue par un conducteur ohmique (fil, résistance…) est entièrement convertie en chaleur. C’est l’effet Joule.

Cette conversion d’énergie est parfois recherchée (dispositif de chauffage électrique). Le plus souvent, cette conversion est indésirable car elle représente une perte d’énergie et de la chaleur à dissiper (dans un ordinateur par exemple).

Dans un générateur réel de tension, comportant une résistance interne, le débit de courant électrique s’accompagne d’une production d’énergie thermique par effet Joule : le générateur chauffe. Plus le courant fourni est intense, plus le générateur chauffe.

En utilisant l’expression de la puissance électrique $*P_e = U·I*$ et la loi d’Ohm $*U = R·I*$, on obtient l’expression de la puissance électrique convertit en puissance thermique dans un conducteur ohmique :

$µ P_j=R·I^2= \frac {U^2}R µ$

Effet Joule

1. Quelle est la résistance électrique d’un grille pain d’une puissance de 500 W prévu pour fonctionner en 220 V ? Quelle est l’intensité du courant consommé ?

2. Quelle est la puissance électrique fournie par un générateur de tension dont la tension de fonctionnement vaut 5,95 V et dont la résistance interne vaut 0,50 Ω et la force électromotrice est de 6,0 V ? Quelle est la puissance thermique dissipée ? Quelle part de la puissance totale produite représente-t-elle ?

Correction

1. Le grille-pain produit de la chaleur par effet Joule. $*R = \frac {U^2}{P_J} =*$ 220²÷500 = 97 Ω

2. On sait que $*P = UI*$. Il faut donc calculer $*I*$. On se sert de la relation $*U=E-rI*$ pour trouver $*I = \frac {E-U}r = *$ 0,1 A.
On en déduit la puissance fournie par le générateur : $*P = UI =*$ 0,595 W
La puissance thermique dissipée par le générateur vaut $*P_J = rI^2 =*$ 5·10^-3 W.
La puissance totale du générateur vaut 0,595 + 0,005 = 0,600 W.
La puissance thermique dissipée représente donc 0,005÷0,600×100 = 0,8 % de la puissance totale.

Rendement d’un dispositif

Définir le rendement d’un convertisseur.

TP Rendement d’un convertisseur

Évaluer le rendement d’un dispositif.

Objectif : déterminer le rendement d’un moteur électrique et d’un transformateur redresseur en fonction de la puissance de sortie demandée.

Matériel disponible

Moteur électrique pouvant fonctionner en 6 V et en 12 V
Voltmètre
Ampèremètre
Ficelle
Jeu de masses (entre 2 g et 200 g)
Générateur 6 V /12 V
Boitier de résistances variables.
Wattmètre (sur prise de 220 V)

1. Rendement d’un moteur électrique

À l’aide du matériel mis à disposition, déterminez si le rendement du moteur électrique dépend de l’effort qu’on lui demande et de la tension d’alimentation.

Vous rédigerez un protocole des expériences réalisées et vous présenterez vos résultats sous forme de graphiques réalisés dans un tableur.

Rappel éventuellement utile 😇 : l’énergie potentielle de pesanteur d’un objet de masse $*m*$ vaut $*E_{PP} = mgz*$

2. Rendement d’un générateur / transformateur

Les générateurs 6 V / 12 V du labo reçoivent de l’énergie électrique sous une tension de 220 V alternative et fournissent cette énergie sous la forme d’une tension continue de 6V ou de 12 V.

Déterminez si le rendement de ces générateurs dépend de la puissance qu’ils délivrent.

Vous rédigerez un protocole des expériences réalisées et vous présenterez vos résultats sous forme de graphiques réalisés dans un tableur.

Éléments de correction

Partie 1

Il faut pouvoir calculer l’énergie électrique reçue par le moteur et l’énergie mécanique qu’il fournit.
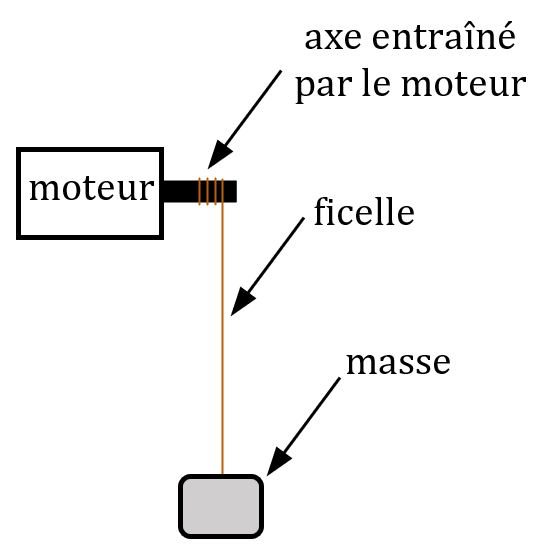
Pour ça, on mesure l’intensité du courant qui traverse le moteur, la tension à ses bornes et la durée de son fonctionnement (si on ne fait pac confiance à l’indication du générateur). Grâce aux relations $*P=UI*$ et $*E=P\Delta t*$, on peut calculer l’énergie électrique reçue.

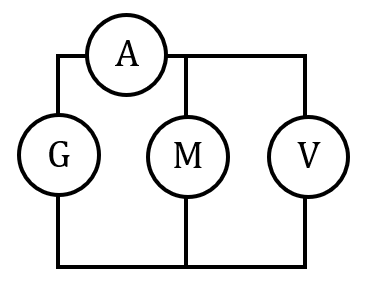
Pour déterminer l’énergie mécanique fournie par le moteur, on lui fait soulever une petite masse attachée à une ficelle. Puis on détermine quelle est l’énergie mécanique fournie par le moteur en calculant la variation d’énergie mécanique de la masse. Pour ça, il faut mesurer la hauteur qu’a gagnée la masse pendant la durée de fonctionnement du moteur. On peut calculer l’énergie cinétique de la masse, mais on s’aperçoit que celle-ci est négligeable devant la variation d’énergie potentielle.

Résultats en 12 V

Avec un masse de 100 g, on trouve un rendement de 13 % environ.
Avec un masse de 200 g, on trouve un rendement de 19 % environ.
Avec un masse de 300 g, on trouve un rendement de 23 % environ.

Conclusion : le rendement d’un moteur dépend de l’effort qu’il fournit.

Partie 2

Résultats des mesures par groupe

Convertisseur : un convertisseur désigne n’importe quel dispositif capable de transformer l’énergie qu’il reçoit en une (ou plusieurs) autre(s) forme(s) d’énergie.

Exemples de convertisseurs électriques
Moteur électrique	Énergie mécanique, chaleur
Ampoule	Énergie lumineuse, chaleur
Radiateur électrique	Chaleur
Batterie (en charge)	Énergie chimique, chaleur
Haut-parleur	Énergie sonore, chaleur
Électro-aimant	Énergie magnétique, chaleur

Rendement d’un convertisseur

Un convertisseur transforme une partie de l’énergie qu’il reçoit en énergie « utile » (énergie mécanique pour un moteur, énergie lumineuse pour une ampoule, etc…). Une partie de l’énergie reçue est perdue sous forme de chaleur (par effet Joule s’il s’agit d’un dispositif électrique, mais aussi par frottement s’il y a des mouvements).

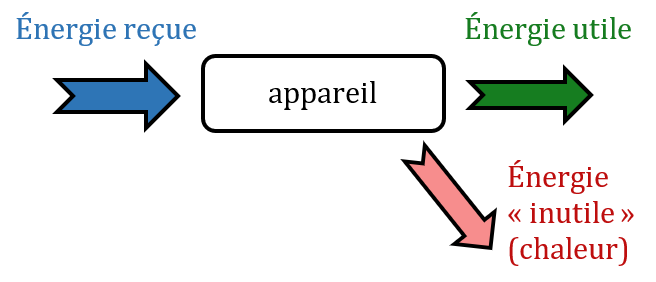
Schéma-bilan énergétique d’un convertisseur

Le rendement $*\eta*$ (êta) d’un convertisseur est défini par :

$µ \eta = \frac {E_\text{utile}}{E_\text{reçue}} µ$

Il peut varier mathématiquement entre 0 et 1 (100 %), mais un convertisseur de rendement 0 serait totalement inutile et un convertisseur de rendement 1 serait un convertisseur parfait sans dégagement de chaleur par effet Joule. Cela n’existe pas sauf pour les convertisseurs dont le but est justement de produire de la chaleur (radiateur électrique, par exemple).

Rendement d’une chaîne de convertisseurs

Dans une chaîne de convertisseurs (par exemple : panneau solaire – batterie – moteur électrique), le rendement global est le produit des rendements des différents éléments de la chaîne.

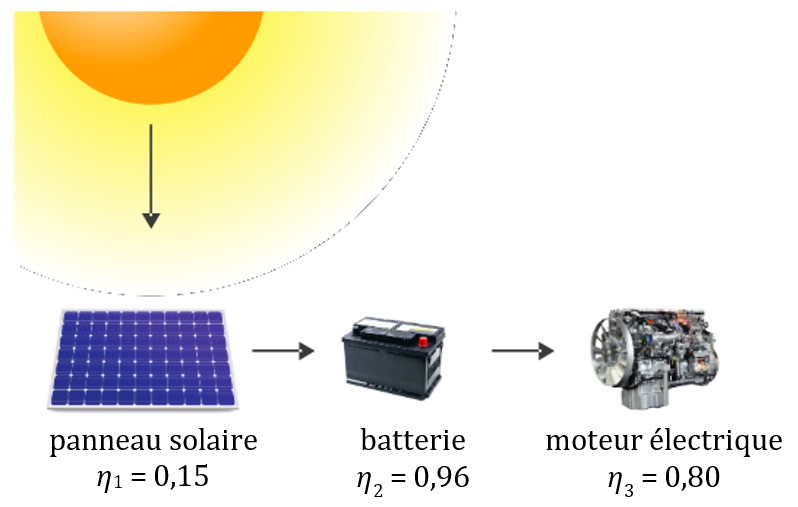
Rendement global de cette chaîne : $*\eta_\text{total} = \eta_1× \eta_2× \eta_3 =*$ 0,115 (soit 11,5 %)

Lampe à dynamo

Une lampe à dynamo est composée d’une dynamo actionnée par une manivelle, d’une batterie rechargeable et d’une LED de 1 W (1 W est la puissance électrique consommée par la LED).
Lorsqu’on actionne la dynamo pendant 30 secondes avec une puissance mécanique de 30 W, on obtient une autonomie de 5 minutes d’éclairage avec la LED.

1. Représenter la chaîne énergétique de la lampe.

2. Calculer le rendement global du dispositif, sachant que la LED a un rendement de 0,8.

Correction

1. Chaîne énergétique de la lampe

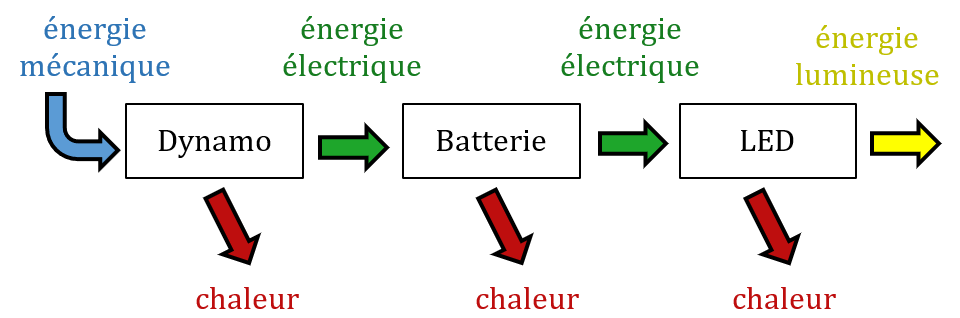
2. Énergie mécanique reçue par la lampe : $*E_m = P_m·\Delta t =*$ 30×30 = 900 J
Énergie lumineuse fournie par la lampe : $*E_\ell = P_\ell·\Delta t’ =*$ 1×0,8×300 = 240 J
Rendement global de la lampe : $*\eta*$ = 240/900 = 0,27 (27 %)

Alimentation de PC sans ventilateur

Extraits d’une présentation sur un site d’e-commerce

L’alimentation Platinum 400 Fanless garantit un rendement minimum de 90% (norme 80 PLUS Platinum). Résultat : une meilleure efficacité pour une réduction de la consommation électrique et moins de chaleur émise par le bloc.

Avec 400W sous le capot, ce modèle développe une puissance suffisante pour les configurations bien équilibrées. L’unique rail +12V fournit un courant de 33 A.

Norme 80 PLUS Platinum

Taux d’utilisation de l’alimentation	20 %	50 %	100 %
Rendement	90 %	94 %	91 %

On souhaite monter un PC dont l’utilisation sera essentiellement de la bureautique et du visionnage de vidéo. La puissance nécessaire varie alors entre 45 et 90 W.

1. La puissance indiquée de 400 W correspond-elle à la puissance maximale fournie ou la puissance maximale consommée par l’alimentation ?

2. Quels sont les avantages d’une alimentation à haut rendement ?

3. Calculer la puissance consommée par l’alimentation lorsqu’elle fournit 80 W.

4. Dans les mêmes conditions, calculer la puissance thermique dissipée et la comparer à une alimentation « standard » fonctionnant dans les mêmes conditions et dont le rendement est de 80 %.

Correction

1. D’après les indications, l’alimentation peut fournir 33 A sous une tension de 12 V. Cela fait une puissance fournie de $*P*$ = 12×33 = 396 W.
Lorsqu’elle fournit cette puissance, elle consomme une puissance de 396÷0,91 = 435 W. Donc la puissance indiquée est la puissance fournie (avec une légère exagération commerciale…).

2. Une consommation électrique réduite et moins de chaleur produite donc pas de nécessité d’un ventilateur : le PC devient très silencieux.

3. Lorsqu’elle fournit 80 W, le taux d’utilisation de l’alimentation est de 20 % (100 % = 400 W). Donc son rendement est de 90 %.
Elle consomme donc une puissance de 80÷0,9 = 89 W.

4. La puissance thermique dissipée par l’alimentation est de 89 – 80 = 9 W environ.
Une alimentation standard consomme, dans les mêmes conditions : 80÷0,8 = 100 W.
La puissance thermique dissipée vaut donc 100 – 80 = 20 W, soit plus du double de l’alimentation Platinum 400 Fanless.

Révision & entraînement

Voiture électrique

La Zoe est une petite voiture électrique fabriquée par Renault.

Le modèle haut de gamme dispose d’une motorisation de 100 kW et d’une batterie d’une capacité de 52 kW·h, dont la force électromotrice vaut $*E*$ = 400 V.

Données : 1 kW·h = 3,6·10⁶ J

1. Capacité de la batterie

1.1. Lorsque cette batterie délivre un courant de 1,0 A, quelle est la puissance qu’elle délivre ? On négligera la baisse de tension à ses bornes due à la résistance interne.

1.2. D’après les données de l’exercice, calculer la durée de la décharge totale de la batterie dans ces conditions.

1.3. Sachant qu’une mole d’électrons a une charge de 96,5·10³ C, calculer la quantité de matière d’électrons que la batterie peut faire circuler de sa borne ⊖ à sa borne ⊕ durant sa décharge.

2. Résistance interne de la batterie

2.1. Calculer l’intensité fournie par la batterie lorsque le moteur est utilisé à pleine puissance (100 kW de puissance électrique reçue), en négligeant toute perte par effet Joule et en supposant que la batterie est un générateur idéal de tension.

En réalité, la batterie se comporte comme un générateur réel de tension, dont la résistance interne est très faible.

2.2. En supposant que lorsque le moteur reçoit 100 kW de puissance électrique, la tension aux bornes de la batterie vale 350 V, calculer l’intensité du courant fourni par la batterie dans ces conditions, puis en déduire la résistance interne de la batterie.

2.3. Outre la diminution de la tension aux bornes de la batterie lorsque le courant délivré est très intense, quelle autre conséquence non désirée a la présence de cette résistance interne ?

2.4. Calculer le rendement de la batterie dans ces conditions d’utilisation, défini comme le rapport de l’énergie reçue par le moteur sur l’énergie totale produite par la batterie (ce qui inclut l’énergie dissipée par effet Joule).

3. Rendement énergétique

On considère la chaîne énergétique commençant à la prise électrique servant à la recharge de la batterie jusqu’à la sortie du moteur fournissant de l’énergie mécanique. Lors d’un cycle de charge et de décharge moyen, le rendement de la batterie est de 0,8. Le rendement du moteur vaut également 0,8.

On peut lire, dans la description technique de la voiture : « Consommation mixte : 17,7 kWh/km »
Ceci correspond à l’énergie électrique donnée par la batterie au moteur pour parcourir un kilomètre dans des conditions « moyennes ».

3.1. Schématiser cette chaîne énergétique.

3.2. Définir le rendement du moteur, puis calculer l’énergie mécanique fournie par le moteur dans ces conditions, pour 1 km parcouru.

3.3. Quelle est l’énergie consommée par l’ensemble de cette chaîne énergétique dans ces conditions ?

Correction

1.1. $*P = UI*$ = 400×1 = 400 W

1.2. $*\Delta t= \dfrac EP*$ = 52·10³÷400 = 130 h (468·10³ s)

1.3. 1A = 1 C·s^-1 donc, 1 A pendant 468·10³ s ça fait une charge de 468·10³ C. Sachant qu’une mole d’électron a une charge de 96,5·10³ C, ça fait 468÷96,5 = 4,85 mol d’électrons

2.1. $* I = \dfrac PU*$ = 100·10³÷400 = 250 A

2.2. $*P*$ = 100 kW et $*U*$ = 350 V, donc $*I*$ = 286 A. $*U = E-rI*$ donc $* r = \dfrac{E-U}I *$ = 50÷286 = 0,175 Ω

2.3. La batterie chauffe.

2.4. Puissance perdue par effet Joule : $*P_J*$ = 0,175×286² = 14,3 kW. Puissance électrique transmise au moteur : 100 kW. Puissance totale produite par la batterie : 114,3 kW. Rendement : 100÷114,3 = 87,5 %.

3.1. Schéma de la chaîne énergétique

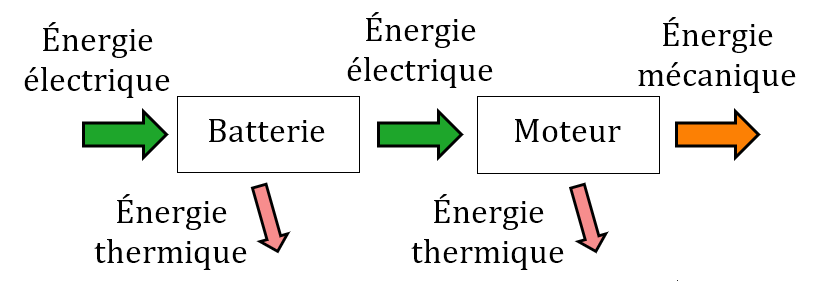
3.2. Rendement du moteur : énergie mécanique fournie ÷ énergie électrique reçue.
Énergie mécanique fournie = 17,7×0,8 = 14,2 kWh

3.3. Pour pouvoir fournir une énergie mécanique de 17,7 kWh, la batterie doit recevoir 17,7÷0,8 = 22,1 kWh.