P5. Énergie mécanique
L’énergie mécanique d’un objet est l’énergie liée à la position et au mouvement de cet objet. Elle a deux composantes : l’énergie cinétique et les différentes formes d’énergie potentielle.
Énergie mécanique
- Utiliser l’expression de l’énergie cinétique d’un système modélisé par un point matériel.
- Établir et utiliser l’expression de l’énergie potentielle de pesanteur pour un système au voisinage de la surface de la Terre.
Énergie cinétique
Un objet en mouvement possède une énergie liée à sa vitesse, appelée énergie cinétique.
| $µ E_C = \frac 12 mv^2 µ$ | $*E_C*$ : énergie cinétique (J) $*m*$ : masse du système (kg) $*v*$ : vitesse du système (m·s-1) |
Rappelez-vous que la vitesse d’un objet ou d’un système dépend du référentiel dans lequel on étudie son mouvement. Donc l’énergie cinétique d’un objet dépend elle-aussi du référentiel d’étude.
Cette expression suppose que le système est assimilé à un point et donc que l’on néglige toute énergie cinétique du système due à la rotation du système sur lui-même.
Énergies potentielles
Il existe plusieurs types d’énergies potentielles : l’énergie potentielle de pesanteur, l’énergie potentielle élastique (accumulée par un ressort tendu, par exemple), l’énergie potentielle électrique (acquise par une particule chargée dans un champ électrique). Nous allons seulement étudier l’énergie potentielle de pesanteur.
Énergie potentielle de pesanteur
L’énergie potentielle de pesanteur d’un système est l’énergie liée à la position de ce système dans un champ de pesanteur. Vous n’aurez aucune difficulté à comprendre intuitivement qu’un rocher au sommet d’une montagne possède plus d’énergie potentielle qu’un rocher dans une plaine, car il peut potentiellement tomber (et provoquer des dégâts), ce qui ne peut pas arriver au rocher dans la plaine.
| $µ E_{pp} = mgz µ$ | $*m*$ : masse (kg) $*g*$ : intensité du champ de pesanteur (N·kg-1) $*z*$ : altitude (m) |
L’altitude d’un objet est définie par rapport à une origine des altitudes arbitraires. L’$*E_{pp}*$ dépend donc de ce choix de l’origine des altitudes.
On se placera toujours dans une situation où on peut considérer l’intensité du champ de pesanteur $*g*$ comme constante, c’est-à-dire sur domaine de variation d’altitude « petit » par rapport au rayon de la Terre (au maximum quelques kilomètres – ce qui laisse quand-même une marge importante. 😊).
Énergie mécanique
Comme je l’ai dit dans l’introduction du chapitre, l’énergie mécanique d’un système, c’est la somme de son énergie cinétique et de ses différentes énergies potentielles.
Quelques exemples
1. Calculer l’énergie cinétique d’un coureur de 70 kg se déplaçant à 25 km·h-1. Comparer cette énergie cinétique à celle d’une balle de fusil de 5,0 g ayant une vitesse de 400 m·s-1.
2. Calculer l’énergie mécanique d’un ballon se trouvant à 5,0 m au-dessus du sol et ayant une vitesse de 6,0 m·s-1 et une masse de 0,5 kg. On se placera dans le référentiel terrestre, avec le sol pour origine des altitudes.
Correction
1. Il faut d’abord convertir la vitesse en m·s-1 (÷3,6) : 25 km·h-1 = 6,94 m·s-1.
$*E_C = \frac 12 m v^2 =*$ 0,5×70×6,942 = 1688 J.
Pour la balle : $*E_C = \frac 12 m v^2 =*$ 0,5×5,0·10-3×4002 = 400 J.
On constate que l’énergie cinétique du coureur est 4 fois plus grande que celle d’une balle de fusil !
2. $*E_C*$ = 0,5×0,5×62 = 9 J et $*E_{PP}*$ = 0,5×9,8×5 = 24,5 J
Donc l’énergie mécanique du ballon vaut $*E_M = E_C + E_{PP} =*$ 33,5 J
TP Étude énergétique d’une chute verticale
- Utiliser un dispositif (smartphone, logiciel de traitement d’images, etc.) pour étudier l’évolution des énergies cinétique, potentielle et mécanique d’un système dans différentes situations : chute d’un corps, rebond sur un support, oscillations d’un pendule, etc.
Objectif : étudier l’énergie mécanique d’un objet au cours d’un mouvement de chute verticale.
Travail demandé
En vous servant de Regressi et d’un tableur, vous construirez un graphique montrant l’énergie cinétique, l’énergie potentielle de pesanteur et l’énergie mécanique d’une balle en chute verticale (lien vers la vidéo). On prendre comme masse de la balle 150 g. Pour l’échelle de distance, prendre 74 cm comme hauteur de la table. Suivre les étapes ci-dessous :
- Pointez le mouvement de la balle sur Regressi, puis exportez les valeurs obtenues dans un tableur.
- Pour effacer les petites erreurs de pointage, modélisez la coordonnée de hauteur $*y*$ en fonction du temps et calculer la valeur de cette grandeur pour les différentes valeurs de $*t*$ (on notera $*y_m*$ cette grandeur).
- Calculer la vitesse de chute $*v_y*$ à chaque instant $*t_i*$ en prenant la vitesse moyenne entre $*t_{i-1}*$ et $*t_{i+1}*$
- Calculer pour chaque instant l’énergie cinétique de la balle, son énergie potentielle de pesanteur et son énergie mécanique, puis afficher le graphique montrant ces trois énergies en fonction du temps.
Éléments de réponses
Voir ce fichier pour les résultats du TP.
Travail d’une force
- Utiliser l’expression du travail $*W_{\mathrm{AB}}(\overrightarrow{F})=\overrightarrow{F}·\overrightarrow{\mathrm{AB}}*$ dans le cas de forces constantes.
- Calculer le travail d’une force de frottement d’intensité constante dans le cas d’une trajectoire rectiligne.
- Capacité mathématique : utiliser le produit scalaire de deux vecteurs.
Le travail d’une force correspond à de l’énergie communiquée à un système par cette force au cours d’un déplacement.
Pour une force constante et au cours d’un déplacement rectiligne, ce travail se calcule par la relation :
Si le travail d’une force est positif, on dit qu’il est moteur : la force favorise le déplacement du système.
S’il est négatif, on dit qu’il est résistant.
Remarque de math : le produit scalaire de deux vecteurs $*\vec{u}*$ et $*\vec{v}*$ est noté $*\vec{u}·\vec{v}*$. C’est un nombre (et non pas un vecteur) égal à $* \Vert \vec{u}\Vert·\Vert\vec{v}\Vert·\cos (\widehat{\vec{u};\vec{v}}) *$
Imaginons un système noté M se déplaçant en mouvement rectiligne d’un point A à un point B. Ce système est soumis à quatre forces constantes comme le montre le schéma ci-dessous. Ce système pourrait être votre chien que vous tirez à la laisse et qui résiste. 😊
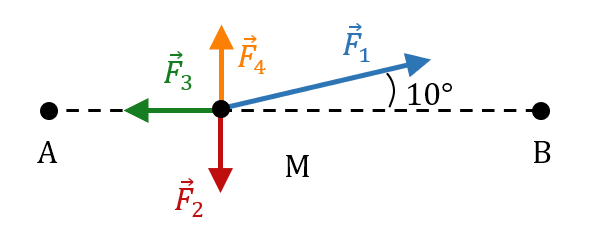
On va chercher l’expression du travail de ces trois forces au cours de ce déplacement
Pour $*\vec{F_1}*$ : $* W_{\mathrm{AB}}(\vec{F_1})= F_1·\mathrm{AB}·\cos(10°)*$. Ce travail est moteur.
Pour $*\vec{F_2}*$ et $*\vec{F_4}*$ : L’angle entre ces forces et le vecteur déplacement $*\overrightarrow{\mathrm{AB}}*$ vaut 90°, donc le produit scalaire entre ces vecteurs est nul. Ces forces ne travaillent pas.
Pour $*\vec{F_3}*$ : $* W_{\mathrm{AB}}(\vec{F_3})= F_3·\mathrm{AB}·\cos(180°) = -F_3·\mathrm{AB} *$. Ce travail est résistant.
Descente en luge
Un enfant sur une luge glisse sans frottement le long d’une pente rectiligne faisant un angle $*\alpha*$ = 15° avec l’horizontale. Il parcourt une distance $*\mathrm{AB}*$ = 30 m. La masse de l’ensemble {enfant + luge} vaut $*m*$ = 50 kg.
On prendra comme valeur de l’intensité de la pesanteur $*g*$ = 10 N·kg-1.
1. Schématiser la situation en faisant figurer les forces qui s’exercent sur le système.
2. Calculer le travail de chacune de ces forces.
Correction
1. Schéma de la situation
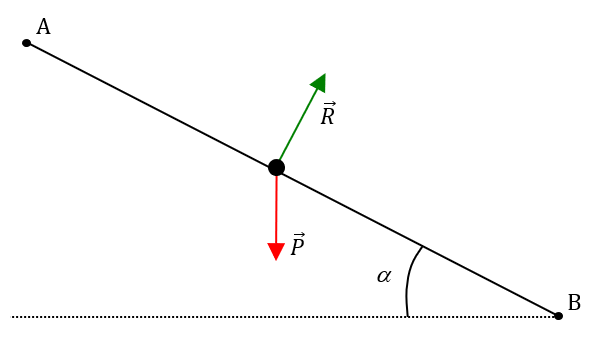
$*\vec{P}*$ est le poids du système (vertical, vers le bas) et $*\vec{R}*$ est la réaction de la piste (perpendiculaire à la piste).
2. Le travail de $*\vec{R}*$ est nul car l’angle entre $*\vec{R}*$ et le vecteur déplacement $*\overrightarrow{\mathrm{AB}}*$ est de 90°.
L’angle entre $*\vec{P}*$ et $*\overrightarrow{\mathrm{AB}}*$ vaut 90 – 15 = 75° donc $*W_{AB}(\vec{P}) = P·\mathrm{AB}·\cos(75°) \simeq*$ 3,8 kJ
Freinage d’une voiture
Une voiture se déplace sur une route horizontale. 50 m avant un virage, le conducteur freine avec une force constante de 3,0 kN jusqu’à l’entrée du virage. Calculer le travail des forces de freinage. On considère que le déplacement est rectiligne tout au long du freinage.
Correction
L’angle est la force de freinage $*\vec{f}*$ et le déplacement est de 180°, donc $*W(\vec{f})*$ = –3·103×50 = – 150 kJ
Forces et énergie mécanique
- Énoncer et exploiter le théorème de l’énergie cinétique.
- Identifier des situations de conservation et de non conservation de l’énergie mécanique.
- Exploiter la conservation de l’énergie mécanique dans des cas simples : chute libre en l’absence de frottement, oscillations d’un pendule en l’absence de frottement, etc.
- Utiliser la variation de l’énergie mécanique pour déterminer le travail des forces non conservatives.
Forces conservatives et non conservatives
Les forces extérieures qui s’appliquent sur un système peuvent modifier son énergie mécanique et/ou les différentes composantes de son énergie mécanique.
Il faut bien distinguer deux types de forces :
- Les forces conservatives : le travail de ces forces ne fait pas varier l’énergie mécanique du système, elles ne font que transformer l’énergie potentielle en énergie cinétique ou inversement. Ces forces sont associées à une énergie potentielle. Il n’y en a donc pas beaucoup : la seule force conservative que vous devez retenir en 1e, c’est le poids.
- Les forces non conservatives : ce sont toutes les autres forces. Leur travail, s’il n’est pas nul, peut modifier l’énergie mécanique du système sur lequel elles s’appliquent.
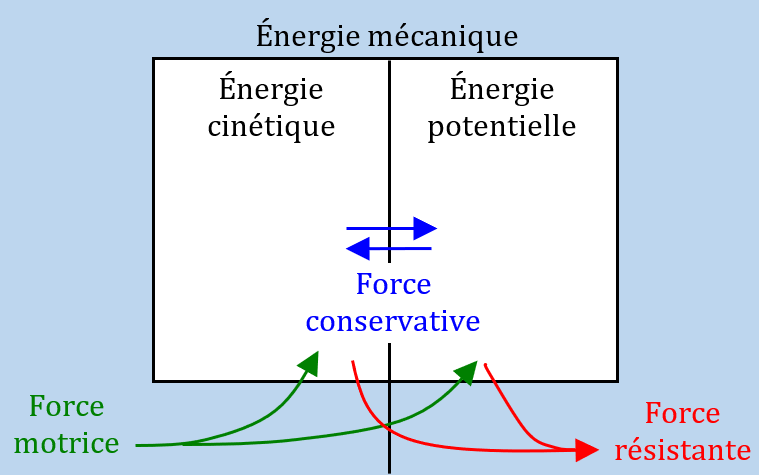
Si le travail d’une force est positif, on dit que la force est motrice (elle favorise le mouvement). Ce travail augmente l’énergie mécanique du système.
À l’inverse, si le travail d’une force est négatif, on dit que la force est résistante (elle s’oppose au mouvement). Ce travail diminue l’énergie mécanique du système.
Travail de forces et énergie mécanique
Par conséquent, si parmi les forces qui s’appliquent sur un système, la seule force ayant un travail non nul est le poids, alors l’énergie mécanique du système se conserve.
Théorème de l’énergie cinétique
Remarque : ce « théorème » est la conséquence des deux paragraphes précédents.
Freinage d’une voiture (2e partie)
Reprendre les données de l’exercice « Freinage d’une voiture » et déterminer la vitesse de la voiture en km/h au moment de son entrée dans le virage, sachant que sa vitesse au début du freinage est de 100 km/h et que sa masse vaut 1200 kg.
Correction
Ici, trois forces s’exercent sur la voiture : son poids, la réaction de la route et la force de freinage. La réaction du support a toujour un travail nul, car elle est toujours perpendiculaire au déplacement. La route est horizontale, donc le poids est aussi perpendiculaire au déplacement et donc son travail est nul aussi.
Seule la force de freinage travaille. On a calculé dans l’exercice précédent que $*W(\vec{f})*$ = – 150 kJ.
D’après le théorème de l’énergie cinétique : $*\Delta E_C = E_{Cf} - E_{Ci} = W(\vec{f})*$
L’énergie cinétique initiale est connue : $*E_{Ci}*$ = 0,5×1200×(100÷3,6)2 = 463 kJ
Donc son énergie cinétique finale vaut 463 – 150 = 313 kJ
$µ E_{Cf} = \frac 12 m v_f^2 \Rightarrow v_f = \sqrt{\frac{E_{Cf}}{\frac 12 m}}µ$
$*v_f*$ = 22,8 m·s-1 soit environ 82 km·h-1
Remarque : on peut tout aussi bien passer par la relation $*\Delta E_M = \sum_i W(\vec{F}_{\mathrm{NC}\,i})*$.
Hauteur atteinte par une balle
Une balle est lancée vers le haut, dans une direction parfaitement verticale, à partir d’une hauteur de 2,0 m et avec une vitesse initiale de 3,0 m·s-1. Les forces de frottement seront négligées.
Déterminer quelle est la hauteur maximale atteinte par la balle, et quelle est sa vitesse au moment où elle touche le sol.
Correction
Dans cette situation très classique, il n’y a qu’une seule force qui s’applique sur la balle : son poids. On est donc dans une situation où l’énergie mécanique se conserve.
Notons (1) la situation initiale, (2) la situation où la balle a atteint la hauteur maximale de sa trajectoire et (3) la situation où la balle touche le sol.
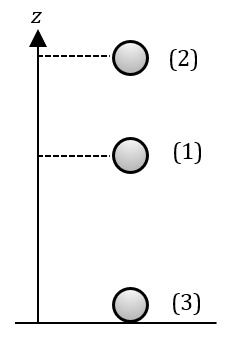
L’énergie mécanique se conserve, donc $*E_{M1}*$ = $*E_{M2}*$ = $*E_{M3}*$
Faisons un bilan énergétique dans un tableau :
| Grandeur | Situation 1 | Situation 2 | Situation 3 |
|---|---|---|---|
| Vitesse (m·s-1) | $*v_1*$ = 3 | $*v_2*$ = 0 | $*v_3*$ = ? |
| Altitude (m) | $*z_1*$ = 2 | $*z_2*$ = ? | $*z_3*$ = 0 |
| $*E_C*$ (J) | $*\frac 12 m v_1^2*$ | 0 | $*\frac 12 m v_3^2*$ |
| $*E_{PP}*$ (J) | $*mgz_1*$ | $*mgz_2*$ | 0 |
| $*E_M*$ (J) | $*\frac 12 m v_1^2 + mgz_1*$ | $*mgz_2*$ | $*\frac 12 m v_3^2*$ |
En utilisant la conservation de l’énergie mécanique, on peut calculer $*z_2*$ et $*v_3*$.
Calcul de $*z_2*$ : $µ \begin{aligned} \frac 12 m v_1^2 + mgz_1 &= mgz_2 \\ \frac 12 v_1^2 + gz_1 &= gz_2 \\ z_2 &= \frac {\frac 12 v_1^2 + gz_1}g \end{aligned} µ$
On trouve $*z_2*$ = 2,46 m.
Calcul de $*v_3*$ : $µ \begin{aligned} \frac 12 m v_1^2 + mgz_1 &= \frac 12 m v_3^2 \\ v_1^2 + 2gz_1 &= v_3^2 \\ v_3 &= \sqrt {v_1^2 + 2gz_1} \end{aligned} µ$
On trouve $*v_3*$ = 6,9 m·s-1.
TP Bilan énergétique d’un système en mouvement
- Capacité numérique : utiliser un langage de programmation pour effectuer le bilan énergétique d’un système en mouvement.
Objectif : Écrire un programme Python permettant
- de calculer la vitesse d’un objet si on connaît son altitude ou inversement son altitude si on connaît sa vitesse (dans les deux cas, l’énergie mécanique est supposée connue), dans le cas de la conservation de l’énergie mécanique ;
- de faire un bilan d’énergie mécanique d’un système en mouvement si l’énergie mécanique ne se conserve pas, si on fournit au programme la vitesse initiale $*v_i*$, l’altitude initiale $*z_i*$, la vitesse finale $*v_f*$ et l’altitude finale $*z_f*$.
Je vous conseille de traiter ces deux aspects séparement, et de les joindre ensuite. Faite d’abord un petit programme qui suppose que l’énergie mécanique se conserve, et qui calcule ou bien une vitesse inconnue si on lui donne deux altitudes et une vitesse, ou bien une altitude inconnue si on lui donne deux vitesses et une altitude.
Ensuite, faite un autre programme qui calcule la variation d’énergie mécanique d’un système en fonction des données nécessaires.
Enfin, rajouter quelques lignes de codes qui choisissent le bon « sous-programme » à utiliser selon ce que lui indique l’utilisateur.
Éléments de réponses
# On peut remplacer les variables en dur par des inputs
reponse = "" # détermine le calcul à faire
vi = 0
zi = 5
g = 9.8
if reponse == "a" : # on cherche zf
vf = 0
zf = (0.5*vi**2 + g*zi - 0.5*vf**2)/g
print("zf =",zf,"m")
elif reponse == "v" : # On cherche vf
zf = 3
vf = (vi**2+2*g*zi-2*g*zf)**0.5
print ("vf =", vf, "m/s")
else : # on cherche à calculer delta Em
vf = 5
zf = 0
m = 40
delta_Em = 0.5*m*vf**2 + m*g*zf - (0.5*m*vi**2 + m*g*zi)
print("Variation d’énergie mécanique :", delta_Em, "J")
Révision & entraînement
Saut en parachute
Un parachutiste de masse $*m*$ = 80 kg suit une trajectoire rectiligne du point A au point B comme montré sur la figure ci-dessous. Durant cette chute, sa vitesse est constante et vaut $*v*$ = 1,5 m·s-1.
Données : AB = 100 m et $*\theta*$ = 10°.
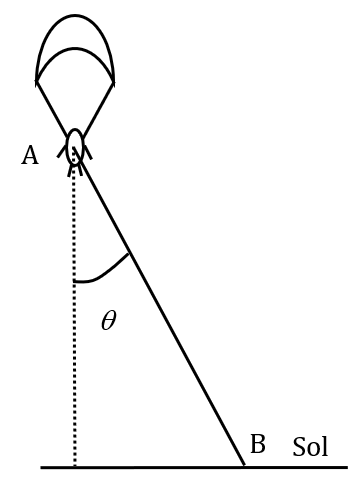
1. Exprimer le travail du poids en fonction de $*\theta*$, $*m*$, $*g*$ et AB.
2. Démontrer que ce travail peut s’écrire $*W_{AB} (\vec{P}) = mg(z_A - z_B)*$.
3. Calculer la valeur du travail du poids sur ce parcours.
4. Calculer la variation d’énergie mécanique du parachutiste entre le point A et le point B juste avant qu’il ne touche le sol (altitude négligeable mais $*v_B*$ = 1,5 m·s-1).
5. Pourquoi cette énergie mécanique n’est-elle pas constante ? En déduire la valeur du travail des forces de frottements.
Correction
1. On applique bêtement la formule du cours : $*W_{AB}(\vec{P}) = mg·\mathrm{AB}·\cos \theta *$
2. Il suffit de remarquer que $* \mathrm{AB}·\cos \theta *$ correspond à la hauteur de A par rapport au sol, autrement dit $*z_A - z_B*$.
3. 77,3 kJ
4. Énergie mécanique initiale : 77,4 kJ ; énergie mécanique au moment de toucher le sol : 90 J. Donc $*\Delta E_m*$ = -77,3 kJ.
5. Elle n’est pas constante à cause des frottements. Travail des forces de frottement : $*W(\vec{f}) = \Delta E_m*$.
Luge
Un enfant descend une pente en luge.
Données
- Vitesse en A : $*v_A \simeq*$ 0
- Vitesse en B : $*v_B*$ = 5 m·s-1
- Dénivelé : $*z_A – z_B*$ = $*h*$ = 5 m
- Angle de la pente avec l’horizontal : $*\alpha*$ = 10°
- Masse du système {luge + enfant} : $*m*$ = 40 kg
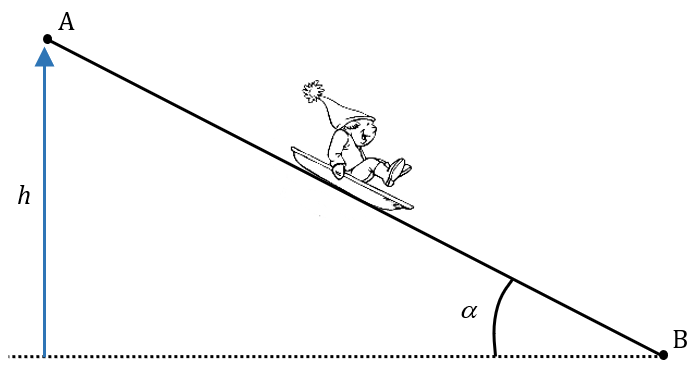
1. Quelle serait sa vitesse en B si les frottements étaient négligeables ?
2. Trouver la valeur moyenne des forces de frottements qui s’exercent sur la luge au cours de la descente.
Correction
1. Sans frottements, il n’y a que le poids $*\vec{P}*$ et la réaction de la piste $*\vec{R}*$. Mais $*\vec{R}*$ ne travaille pas car elle est perpendiculaire à la piste. Donc seul $*\vec{P}*$ travaille et donc l’énergie mécanique se conserve. D’où $*E_{mA} = E_{mB}*$.
Il s’en suit que : $*mgz_A = \frac 12 mv_B^2 + mgz_B*$.
$µ v_B = \sqrt{2g(z_A-z_B)} µ$
$*v_B*$ = 9,9 m·-1.
2. Le travail des forces de frottement est égal à la variation d’énergie mécanique.
$µ \Delta E_m = \frac 12 m v_B^2 - mgz_A µ$
D’où $*\Delta E_m*$ = $*-*$1460 J
La valeur « moyenne » des forces de frottements correspond à celle qu’elles auraient si elles étaient constantes sur tout le trajet. Donc, si on appelle $*f*$ cette valeur moyenne, on a : $*f·\mathrm{AB}·\cos(180°) = -1460*$.
On a d’autre part que $* \sin \alpha = \dfrac h{\mathrm{AB}} *$, ce qui permet d’obtenir $*\mathrm{AB}*$ = 28,8 m.
Ce qui donne $*f*$ = 50,7 N.