P6. Ondes mécaniques
Une onde mécanique, c’est une brève déformation de la matière qui se propage grâce à son élasticité. Elles sont partout autour de nous (sons, vagues, vibrations diverses…)
Propagation d’une onde mécanique
- Décrire, dans le cas d’une onde mécanique progressive, la propagation d'une perturbation mécanique : houle, ondes sismiques, ondes sonores, etc.
- Expliquer, à l’aide d’un modèle qualitatif, la propagation d'une perturbation mécanique dans un milieu matériel.
- Exploiter la relation entre la durée de propagation, la distance parcourue par une perturbation et la célérité, notamment pour localiser une source d’onde.
Qu’est-ce qu’une onde mécanique ?
Lorsqu’une perturbation mécanique (une torsion, une compression, etc.) soudaine est créée dans un milieu matériel, celle-ci peut se propager dans ce milieu.
La propagation de cette perturbation est appelée onde mécanique progressive.
Onde transversale et onde longitudinale
Onde transversale : une onde est dite transversale si la direction de la perturbation est perpendiculaire à la direction de propagation de l’onde.
Onde longitudinale : direction de la perturbation parallèle à la direction de propagation de l’onde.

Onde et énergie
Une onde mécanique transporte de l’énergie, mais ne transporte pas de matière.
Un son, par exemple, est capable de mettre en mouvement vibratoire la membrane d’un micro, ou nos tympans. Mais la position « moyenne » de la membrane ne change pas. De même, la houle (des vagues régulières à la surface de la mer, qui ne déferlent pas) peut provoquer l’oscillation verticale d’un bâteau, mais la position moyenne du bateau ne changera pas. De même, les molécules d’eau ne sont pas emportées par la vague.
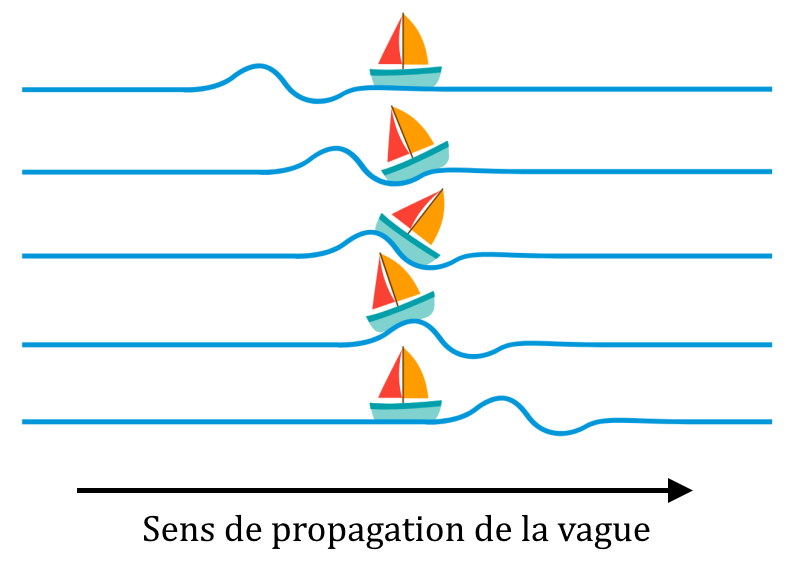
Vitesse de propagation d’une onde
Considérons une vague se déplaçant de la gauche vers la droite :
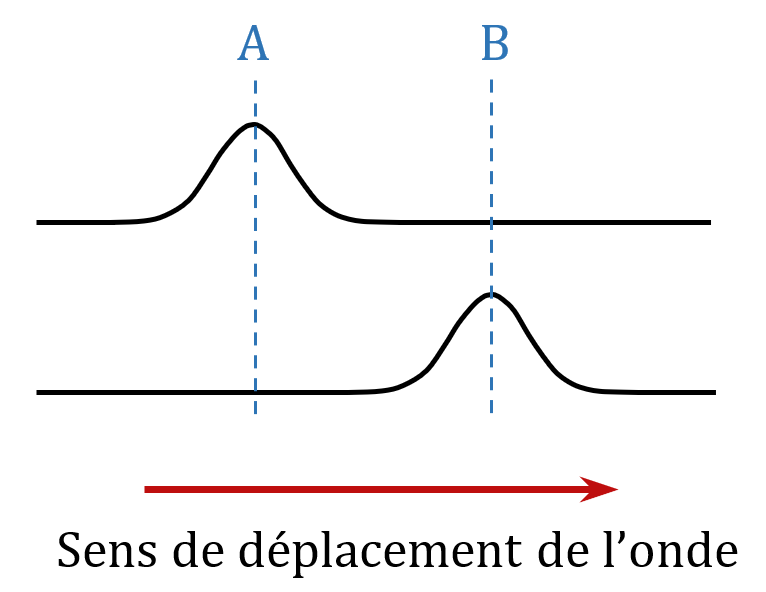
La vague passe au point A au temps $*t_A*$ et passe au point B au temps $*t_B*$. On dit que l’onde arrive en B avec un certain retard $*\tau*$ (prononcer « tau ») par rapport à son passage en A.
$µ \tau = t_B - t_A µ$La vitesse de propagation de l’onde (parfois appelée célérité, notée $*c*$) est donnée par :
$µ v = \frac {d_\mathrm{AB}}\tau µ$La vitesse de propagation d’une onde mécanique dépend principalement de l’élasticité du milieu de propagation, de sa masse volumique et de sa température.
dans l’air, $*v_{air}*$ ≃ 340 m·s-1 dans l’eau, $*v_{eau}*$ ≃ 1,5 km·s-1
TP Propagation d’une onde
- Produire une perturbation et visualiser sa propagation dans des situations variées, par exemple : onde sonore, onde le long d’une corde ou d’un ressort, onde à la surface de l'eau.
- Déterminer, par exemple à l’aide d’un microcontrôleur ou d’un smartphone, une distance ou la célérité d’une onde. Illustrer l’influence du milieu sur la célérité d’une onde.
Objectif : étudier la vitesse de propagation du son dans l’air à différentes températures (et dans l’eau ?)
Matériel disponible
- Oscilloscope
- Émetteur et récepteur à ultrasons
Mesure de la vitesse du son
• Relier l’émetteur à la voie 1 de l’oscilloscope, et le récepteur à la voie 2.
• Placer l’émetteur en mode salve
• Visualiser le signal émis par l’émetteur et celui reçu par le récepteur.
• En mesurant le retard avec lequel le signal arrive au récepteur, déterminer la vitesse de propagation du son. Vous veillerez à faire une estimation de l’incertitude de cette mesure.
Influence du milieu de propagation
• Proposer un protocole permettant de mettre en évidence (au moins de manière qualitative), l’influence de la température de l’air sur la vitesse de propagation du son.
Proposer un protocole permettant de mettre en évidence la différence de vitesse de propagation du son dans l’eau et dans l’air.
Éléments de réponses
Principe du sonar
Un sonar (SOund Navigation And Ranging) est un dispositif qui émet une brève impulsion sonore (ou ultrasonore) et écoute l’écho qui lui parvient, en mesurant le retard $*\Delta t*$ entre l’émission et la réception de l’impulsion sonore.
Les chauves-souris utilisent ce principe pour localiser leur proie et éviter les obstacles. La durée mise par les ondes pour revenir à la chauve-souris permet à cette dernière, après réflexion de l’onde sur une proie, d’apprécier la distance la séparant de cette proie, un papillon par exemple.
Si le signal émis par une chauve-souris lui revient après une durée $*\tau*$ = 16,7 ms, estimer la distance qui sépare la chauve-souris du papillon. On prendra comme vitesse de propagation du son dans l’air $*v*$ = 340 m·s-1.
Correction
Distance parcourue par le son : $*d = v·t =*$ 340×0,0167 = 5,678 m
Mais le son a fait un aller-retour entre la chauve-souris et le papillon. Il faut donc diviser cette distance par 2 !
Ce qui donne 2,839 m arrondi à 2,84 m (3 chiffres significatifs).
Onde mécanique périodique
- Distinguer périodicité spatiale et périodicité temporelle. Justifier et exploiter la relation entre période, longueur d'onde et célérité.
- Déterminer les caractéristiques d'une onde mécanique périodique à partir de représentations spatiales ou temporelles.
- Capacité mathématique : utiliser les représentations graphiques des fonctions sinus et cosinus.
Création d’une onde mécanique périodique
On a vu au paragraphe précédent qu’une onde mécanique était la propagation d’une perturbation mécanique.
Si la perturbation mécanique est périodique, alors l’onde créée est elle-même périodique.
Sur l’animation (lien à droite ou ci-dessous), observez le cas d’une onde mécanique non périodique (lorsque l’émetteur est en mode impulsion) et le cas d’une onde mécanique périodique (lorsque l’émetteur est en mode sinusoïdale).
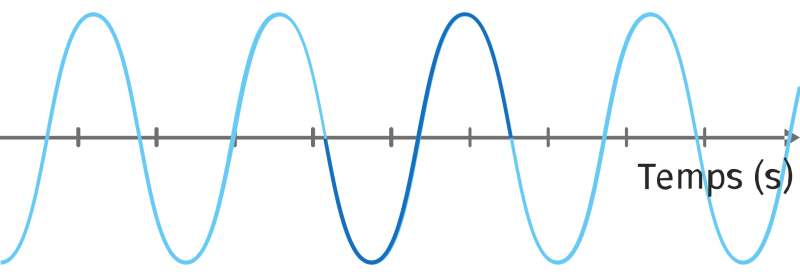
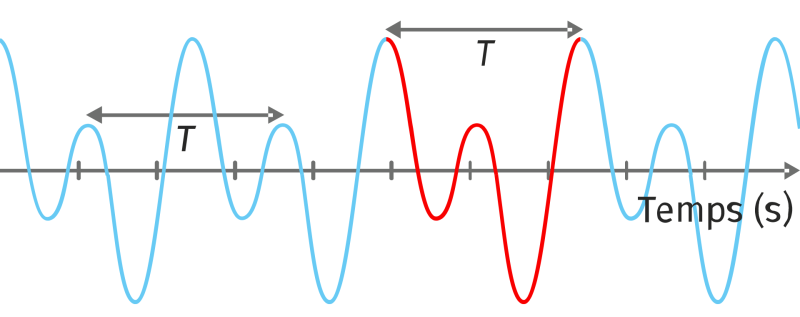
Remarque à propos des ondes sinusoïdales
Dans la nature, les ondes strictement sinusoïdales sont rares. Mais il a été vu en Enseignement scientifique qu’une onde périodique quelconque de fréquence $*f*$ peut être obtenue par une somme d’ondes sinusoïdales de fréquence $*f*$, 2$*f*$, 3$*f*$…
Si on sait correctement modéliser une onde sinusoïdale, on peut alors modéliser n’importe quelle onde périodique.
Caractéristiques d’une onde périodique
Double périodicité d’une onde
Une onde possède une double périodicité.
Elle possède d’abord une périodicité temporelle. Imaginons un bateau immobile en pleine mer. Des vagues périodiques soulèvent régulièrement le bateau. En un point donné, le mouvement vertical du bateau se répète dans le temps. Il s’agit là de l’illustration de la périodicité temporelle d’une onde. À un endroit donné, la perturbation se répète dans le temps. Ce temps correspondant à une répétition s’appelle la période.
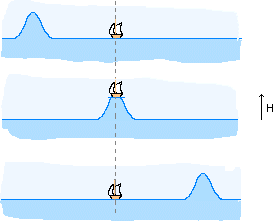
Mais, si l’on fixe le temps, en prenant une photo de la mer, par exemple, on s’aperçoit que les vagues se répètent à distance régulière. C’est ce qu’on appelle la périodicité spatiale de l’onde. À un moment donné, la perturbation se répète dans l’espace. La distance qui sépare les sommets (ou les creux) de deux vagues consécutives s’appelle la longueur d’onde.
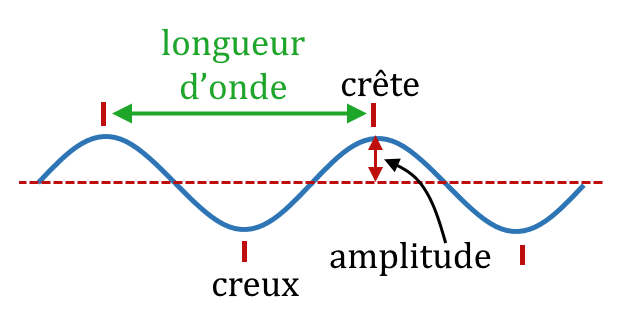
Période, longueur d’onde et vitesse de propagation
Pour l’explication suivante, aidez-vous de l’animation à droite ou ci-dessous.
À $*t*$ = 0, la perturbation périodique commence son cycle. Le début de cette perturbation commence à se propager à une vitesse $*v*$. Pendant toute la durée de la période notée ($*T*$), le début de cette perturbation continue à se propager. Lorsque $*t*$ = $*T*$, la perturbation recommence un nouveau cycle. Le début de la perturbation précédente a parcouru une distance égale à $*v×T*$. Cette distance est la longueur d’onde $*\lambda*$ (lambda).
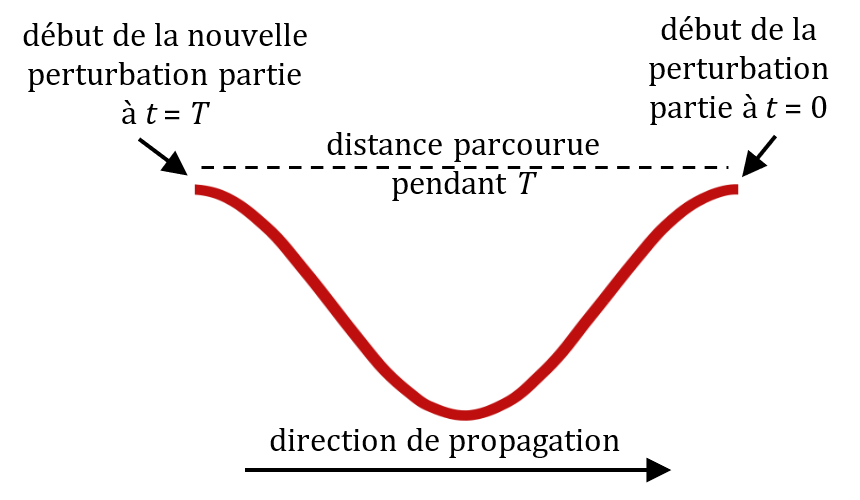
On peut donc conclure que :
| $*\lambda = v×T*$ |
$*\lambda*$ : longueur d’onde (m) $*v*$ : vitesse de l’onde (m·s-1) $*T*$ : période de l’onde (s) |
D’autre par, comme la fréquence f d’un phénomène périodique vaut :
$µ f = \frac 1T µ$On peut également écrire :
| $µ \lambda = \frac vf µ$ |
$*\lambda*$ : longueur d’onde (m) $*v*$ : vitesse de l’onde (m·s-1) $*f*$ : fréquence de l’onde (Hz) |
TP Célérité, longueur d’onde et période
- Déterminer la période, la longueur d’onde et la célérité d’une onde progressive sinusoïdale à l’aide d'une chaîne de mesure.
Objectif déterminer la vitesse des ultrasons par mesure de leur longueur d’onde
Afin de comprendre le principe de ce TP, il est nécessaire de bien comprendre les points suivants (les animations sont là pour vous aider).
- Un microphone produit un signal électrique analogue au signal sonore reçu. Le son et le signal électrique produit ont notamment la même fréquence.
Principe du fonctionnement d’un microphone - Deux microphones percevant la même onde sonore produisent un signal en phase s’ils sont distant d’un nombre entier de longueur d’onde.
Deux points sur une même onde. - Phase et opposition de phase
- Deux courbes sinusoïdales de même période sont en phase si leur maxima et leur minima coïncident dans le temps.
- Deux courbes sinusoïdales de même période sont en opposition de phase si les maxima de l’une coïncident avec les minima de l’autre.
Questions préalables
1. Qu’est ce que la longueur d’onde $*\lambda*$ d’une onde ?
2. À quelle condition les signaux électriques produits par les 2 récepteurs ultrasonores seront-ils en phase ?
3. Quel temps met l’onde à se déplacer d’une longueur égale à $*\lambda*$ ?
4. En déduire un protocole permettant de mesure précisément la vitesse de propagation des ultrasons avec le matériel proposé ci-dessous.
Matériel disponible
Un émetteur et deux récepteurs à ultrasons ; oscilloscope
✋ Conseils
Brancher le récepteur « fixe » sur la voie n°1 de l’oscilloscope et fixez-le avec du scotch.
Les récepteurs ont un maximum de sensibilité pour une fréquence donnée de l’émetteur. Assurez-vous de régler l’émetteur à cette fréquence.
Travail demandé
• Déterminer la vitesse des ultrasons en estimant l’incertitude expérimentale sur cette mesure.
• Comparer le résultat de la mesure à la valeur théorique $* c = 20,05·\sqrt{T} *$ avec $*T*$ la température de l’air en kelvins.
Éléments de réponses
Une gouttière percée
Un jour de pluie, une flaque s’est formée au pied d’un immeuble. La gouttière qui se trouve au-dessus est percée. Des gouttes tombent régulièrement de la gouttière, à raison de 72 gouttes par minute. À chaque fois une petite vague circulaire est créée. Son diamètre grandit. Entre deux vagues successives, on mesure une distance $*d*$ = 20 cm.
1. Une onde mécanique progressive périodique est créée. Justifier chaque terme en caractères gras.
2. Calculer la fréquence de l’onde, puis sa période.
3. Quelle distance a parcouru une vague avant que la suivante prenne naissance ? Quelle durée s’est alors écoulée ?
4. En déduire la célérité de l’onde.
Correction
1. mécanique : il s’agit d’une déformation de la matière (l’eau).
progressive : cette déformation se propage.
périodique : les perturbations sont créées de manière périodique.
2. 72 gouttes par minute → 1,2 gouttes par seconde, soit 1,2 Hz.
La période vaut $*T*$ = 1/$*f*$ = 1/1,2 = 0,83 s
3. $*d*$ = 20 cm = $*\lambda*$. Il s’est écoulé une période, soit 0,83 s
4. $*v*$ = $*\lambda / T*$ = 0,2/0,83 = 0,24 m·s-1.
À propos de la houle
Un marin est sur son bateau en pleine mer. Le bateau est immobile par rapport à l’eau. De la houle soulève périodiquement son bateau. Le marin détermine qu’entre chaque vague, il s’écoule 8 secondes. Les vagues, parallèles entre elles, sont séparées d’une distance de 50 mètres environ.
Donner une estimation de la vitesse de propagation des vagues.
Correction
L’énoncé indique que $*\lambda*$ ≃ 50 m et T ≃ 8 s.Donc $*v*$ = $*\lambda / T*$ ≃ 6 m·s-1
Représenter une onde périodique sur un tableur
Partie 1 : Onde sinusoïdale
Créer un fichier dans un tableur, permettant d’afficher le graphique montrant une fonction de type $*f (t) = a·\sin(b·t+c)*$.
$*a*$, $*b*$ et $*c*$ doivent pouvoir être modifié par l’utilisateur.
Le pas temporel (l’écart $*\Delta t*$ entre deux valeurs consécutives de $*t*$) doit également pouvoir être modifié simplement par l’utilisateur.
1.1. Quelle est l’influence du terme $*a*$, appelé amplitude de l’onde ?
1.2.a. Quelle est l’influence du terme $*b*$, appelé pulsation de l’onde ?
1.2.b. Question optionnelle, pas simple : montrer que la pulsation $*b*$ vaut 2π×fréquence.
1.3. Quelle est l’influence du terme $*c*$, appelé phase de l’onde ?
Partie 2 : Onde périodique quelconque
Créer un fichier dans un tableur permettant d’afficher le graphique de la somme de quatre fonctions sinusoïdales de fréquence $*f*$, 2$*f*$, 3$*f*$ et 4$*f*$.
Cela revient à afficher la fonction :
$*g(t) = a_1·sin(b·t + c_1)*$ $*+ a_2·sin(2b·t + c_2)*$ $*+ a_3·sin(3b·t + c_3)*$ $*+ a_4·sin(4b·t + c_4)*$
Les $*a_i*$ et $*c_i*$ étant des paramètres indépendants qui peuvent être choisis par l’utilisateur, ainsi que le paramètre $*b*$.
La fonction $*g(t)*$ est-elle périodique ? Est-elle sinusoïdale ?
Correction
1.1. $*a*$ influence le minimum et le maximum de la fonction.
1.2.a. $*b*$ influence la période (et donc la fréquence) de la fonction.
1.2.b. D’après la définition de la période $*T*$ de la fonction, $*f (t) = f(t+T)*$ et donc $*a·\sin(b·t+c) = a·\sin(b·(t + T )+c)*$.
Or on sait que $*\sin (x) = \sin (x + 2\pi)*$
Le fait que $*a·\sin(b·t+c) = a·\sin(b·t + b·T + c)*$ signifie que $*b·T = 2\pi*$ et donc que $*b = \frac {2\pi}T = 2\pi f *$
1.3. $*c*$ influence la « position horizontale » de la fonction sinusoïdale. Une variation de $*c*$ translate la courbe vers la droite (si cette variation est négative) ou vers la gauche (si la variation de $*c*$ est positive).
2e partie : on voit graphiquement que la fonction $*g(t)*$ est périodique, bien qu’elle ne soit pas sinusoïdale.