P7. Images & couleurs
Dans ce chapitre, nous allons nous intéresser à la formation d’image grâce à des lentilles convergentes, ainsi qu’à la formation des couleurs.
Lentille convergente
- Exploiter les relations de conjugaison et de grandissement fournies pour déterminer la position et la taille de l’image d’un objet-plan réel.
- Déterminer les caractéristiques de l’image d’un objet-plan réel formée par une lentille mince convergente.
- Capacités mathématiques : utiliser le théorème de Thalès. Utiliser des grandeurs algébriques.
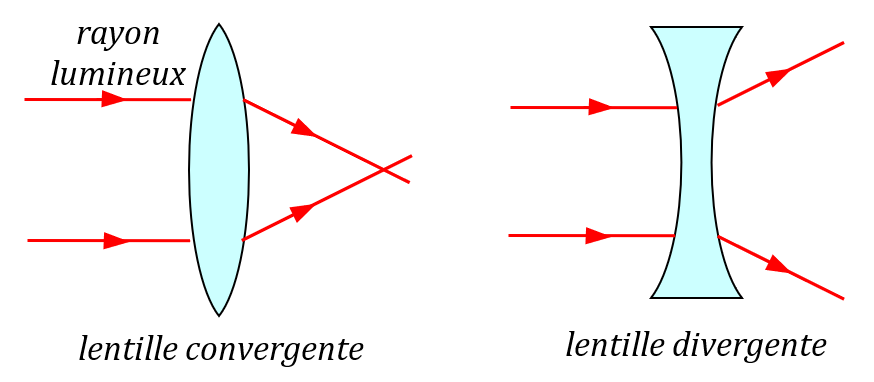
Une lentille optique est un composant fait d’un matériau transparent (le plus souvent un type de verre ou de plastique). Les lentilles sont destinées à faire converger ou diverger la lumière.

Lorsque une onde lumineuse rencontre un dioptre (surface séparant deux milieux homogènes d’indice différent), la lumière est réfractée en suivant les lois de Snell-Descartes. Une lentille est l’association de deux dioptres et par conséquent va faire subir deux réfractions à la lumière qui la traverse.
Lentille mince convergente
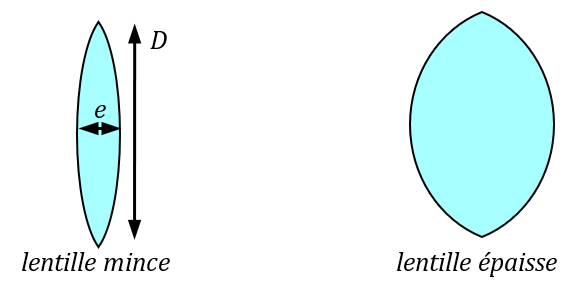
Lentille mince : une lentille est dite mince si son épaisseur est faible devant son diamètre.
Lentille convergente : elle fait converger des rayons lumineux qui arrivent parallèlement entre eux. Une lentille convergente est plus épaisse en son centre que sur ses bords.
Axe et centre optiques
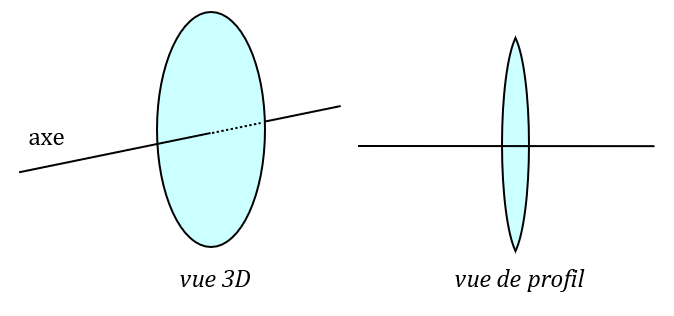
L’axe optique d’une lentille est son axe de symétrie.
Une lentille (convergente ou divergente) possède trois points particuliers : son centre optique O et ses deux foyers F et F’.
Centre optique : noté « O », c’est le point se trouvant au centre de la lentille.
Foyers objet et image
Foyer objet et foyer image : notés respectivement F et F’, ce sont deux points se trouvant sur l’axe optique de la lentille à égale distance du centre optique.
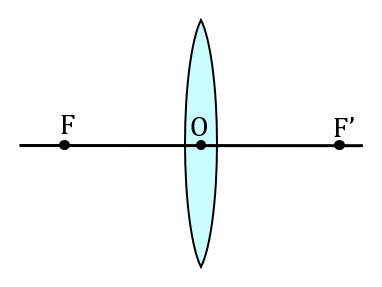
La distance « centre optique – foyer » est appelée distance focale de la lentille et notée $*f*$ ou $*f’*$. Cette distance est propre à la lentille (elle dépend de sa forme). Les lentilles utilisées en TP ont une distance focale comprise entre 5 cm et 50 cm.
Les deux foyers sont physiquement parfaitement équivalents. Celui que se trouve du côté où arrivent les rayons lumineux est appelé « foyer objet » et l’autre « foyer image ». Ce n’est que le sens de propagation de la lumière qui les distinguent.
Remarque : des rayons lumineux qui arrivent parallèlement à l’axe optique de la lentille converge tous au foyer image. Une lentille convergente concentre donc la lumière qu’elle reçoit du soleil, parfois suffisamment pour provoquer l’embrasement d’une feuille de papier.

Construction géométrique d’une image
Tout au long de ce paragraphe, n’hésitez pas à consultez l’animation ci-dessous qui vous permettra de mieux visualiser les notions abordées.
Il existe trois rayons particuliers qui permettent d’obtenir, par construction géométrique, l’image d’un objet formée par une lentille convergente :
- Rayon incident parallèle à l’axe optique : il ressort de la lentille en passant par le foyer image F’.
- Rayon incident passant par le centre optique : il n’est pas dévié.
- Rayon incident passant par le foyer objet F : il ressort de la lentille parallèlement à l’axe optique.
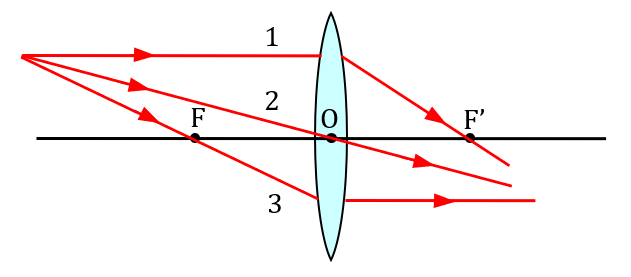
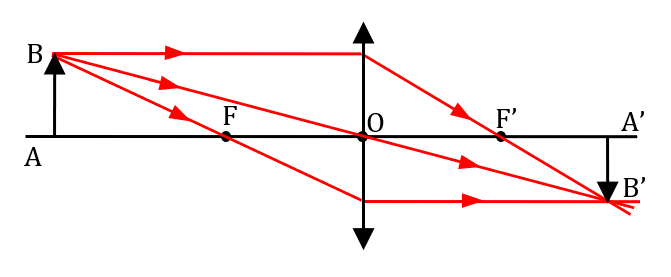
Pour construire géométriquement l’image B’ d’un point lumineux B formé par une lentille, on trace les trois rayons particuliers issus de ce point lumineux avant et après passage dans la lentille.
B’ se forme là où les trois rayons issus de B concourrent. C’est là qu’il faut placer l’écran si l’on veut obtenir une image nette de B.
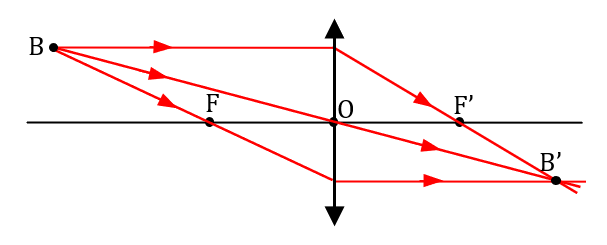
Remarques
• Sur un schéma optique, la lentille est schématisée par une double flèche. Il faut également placer une flèche sur chaque rayon lumineux avant et après la traversée de la lentille.
• Tous les rayons lumineux issus de B et traversant la lentille se croisent en B’. Mais nous ne pouvons les tracer qu’une fois que nous connaissons la position de B’.
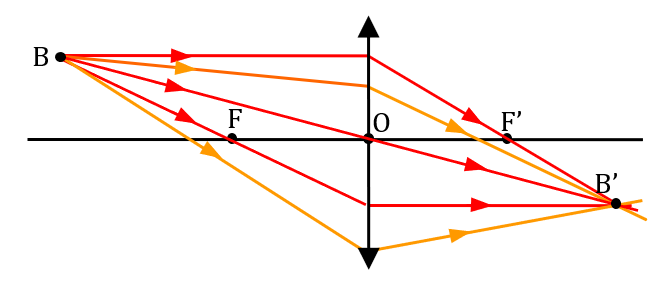
• On peut obtenir l’image B’ en ne traçant que deux rayons particuliers. Mais une construction plus soignée exige de tracer les trois, lorsque cela est possible.
• En optique, on représente souvent un objet lumineux sous forme de flèche verticale partant de l’axe optique. L’image A’ du point A de l’objet se trouvant sur l’axe sera à la verticale du point B’.
TP Lentille convergente
- Estimer la distance focale d’une lentille mince convergente.
- Tester la relation de conjugaison d’une lentille mince convergente.
- Réaliser une mise au point en modifiant soit la distance focale de la lentille convergente soit la géométrie du montage optique.
1. Mettez en place le matériel pour former une image réelle sur l’écran
2. Modifier le montage pour obtenir une image virtuelle. Observez cette image : quel est son sens ? Que peut-on dire de sa taille ?
3. Vous disposez de trois lentilles convergentes. Comment faire pour estimer rapidement leur distance focale ?
4. Vérifier que la relation de conjugaison est respectée dans au moins trois situations différentes.
5. Utiliser la méthode de Silbermann (voir exercice en fin de paragraphe) pour estimer précisément la distance focale d’une des lentilles dont vous disposez. Estimez l’incertitude portant sur cette distance focale.
Correction
Images réelle et virtuelle
En suivant à la lettre la méthode de construction géométrique d’une image, on s’aperçoit que la situation est un peu différente si l’objet est placé entre le foyer objet F et le centre optique O de la lentille : les rayons ne se croisent plus à la sortie de la lentille.
Cependant, un prolongeant virtuellement les rayons émergeants de la lentille, on s’aperçoit qu’ils se croisent tous virtuellement en un même point situé côté « objet » de la lentille. L’image formée est virtuelle.
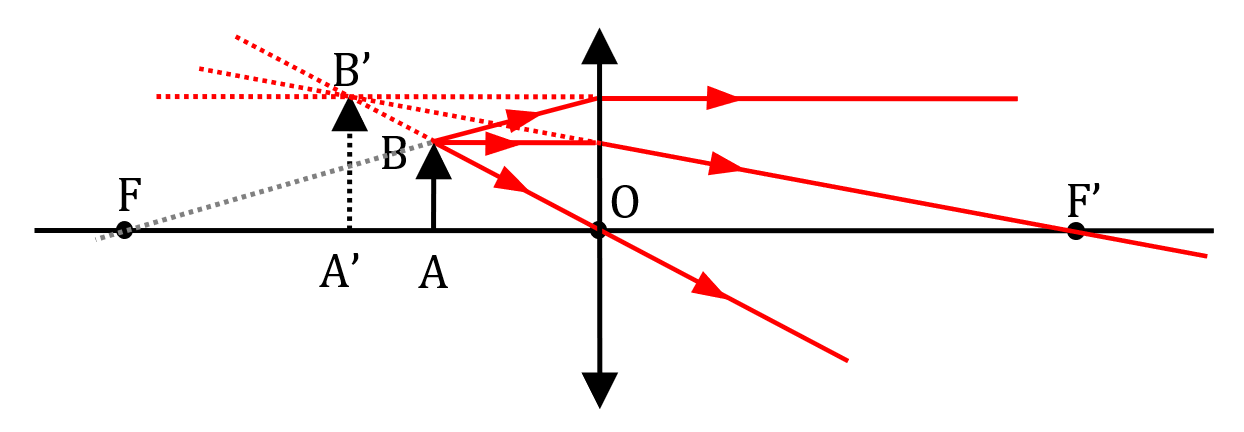
Image réelle : une image réelle est obtenue là où des rayons lumineux se croisent réellement. On ne peut pas l’observer à l’œil nu, mais seulement sur un écran.
Image virtuelle : une image est dite virtuelle si elle est obtenue par croisement « virtuel » de rayons. Elle ne peut pas être recueillie sur un écran mais peut être observée à l’œil nu à travers la lentille.
Construction géométrique
On place un objet lumineux AB de 4,0 cm de haut à 40 cm d’une lentille convergente de focale $*f*$ = 15 cm.
1.a. Faire un schéma de la situation. Échelle horizontale : 1/4, échelle verticale 1/2.
1.b. Par une construction graphique très soignée, prévoir à quelle distance de la lentille va se former l’image, et quelle sera sa taille.
L’objet est maintenant placé à 8,0 cm de la même lentille.
2.a. Faite un schéma de la situation, en utilisant une échelle adaptée.
2.b. Construire l’image obtenue par la lentille. En déduire à quelle distance de la lentille va se former l’image, et quelle sera sa taille.
Correction
1. Schéma
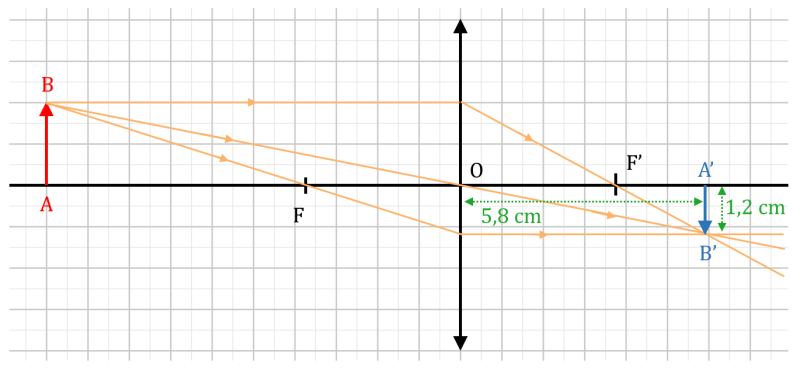
L’image se trouve à environ 5,8 cm sur le schéma, soit 23,2 cm dans la réalité
Sa taille sur le schéma est d’environ 1,2 cm, soit 2,4 cm dans la réalité.
2. Schéma
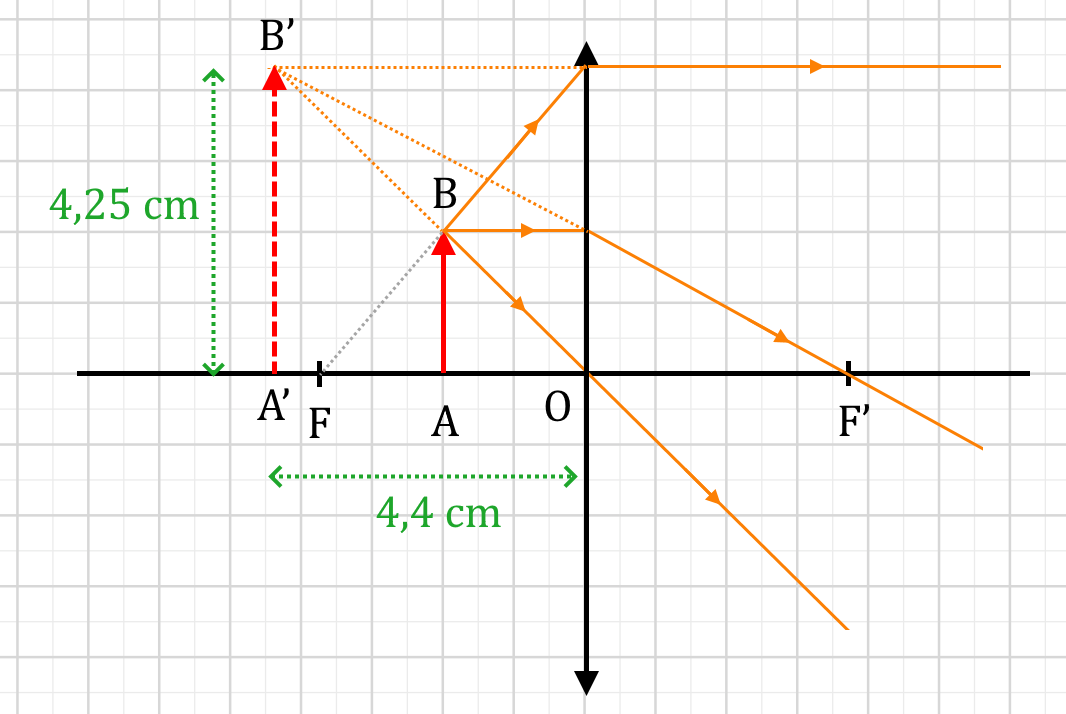
L’image va se trouver à 4,4×4 = 17,6 cm de la lentille.
Sa taille sera de 4,25×2 = 8,5 cm.
Relation de conjugaison
La relation de conjugaison lie les distances algébriques lentille-objet, lentille-image et distance focale.
Une distance algébrique peut être positive ou négative. Elle est comptée négativement lorsque on se déplace dans le sens opposé à celui de propagation de la lumière pour la mesurer.

Sur le schéma ci-dessus, la distance algébrique $*\overline{\text{OA}}*$ est négative (notez la barre au-dessus de $*\text{OA}*$, indiquant qu’on parle d’une distance algébrique), de même que la distance $*\overline{\text{OF}}*$.
Les distances $*\overline{\text{OA’}}*$ et $*\overline{\text{OF’}}*$ sont comptées positivement.
La relation de conjugaison s’écrit :
✋ Il est très important de faire attention au signe de ces valeurs !
Remarques
• Cette relation ne faisant intervenir que des distances, il n’est pas nécessaire de les convertir en mètre. Il faut cependant que toutes les distances soient exprimées dans la même unité.
• Lorsque l’objet est très éloignée de la lentille, alors la valeur de la fraction $*\frac 1{\overline{\text{OA}}}*$ est proche de 0. Donc la relation de conjugaison devient $*\frac 1{\overline{\text{OA’}}} \simeq \frac 1{f}*$ et l’image se forme au foyer de la lentille.
Grandissement
Le grandissement est, par définition, égale au rapport de la taille de l’image sur la taille de l’objet. Attention, il s’agit là aussi de grandeurs algébriques. Si l’image est « à l’envers » par rapport à l’objet, alors $*\overline{\text{AB}}*$ et $*\overline{\text{A’B’}}*$ auront des signes opposés et le grandissement sera donc négatif.
$µ \gamma = \frac {\overline{\text{A’B’}}}{\overline{\text{AB}}} µ$En utilisant le théorème de Thalès, il est facile de montrer que le grandissement vaut également :
$µ \gamma = \frac {\overline{\text{OA’}}}{\overline{\text{OA}}} µ$Relation de conjugaison et grandissement
En utilisant les données de l’exercice précédent :
1. Trouver, en utilisant la formule de conjugaison, la position de l’image par rapport à la lentille, dans les deux cas. 1. Dans le cas où l’objet se situé à 40 cm de la lentille : $* \overline{\text{OA}} *$ = – 40 cm
$µ
\begin{aligned}
\frac 1{\overline{\text{OA’}}} - \frac 1{-40} &= \frac 1{15} \\
\frac 1{\overline{\text{OA’}}} &= \frac 1{15} - \frac 1{40}\\
\frac 1{\overline{\text{OA’}}} &= 0,0417
\end{aligned}
µ$
Donc $*\overline{\text{OA’}}*$ ≃ 24 cm Dans le cas où l’objet se trouve à 8 cm, l’image se trouve à :
$µ \frac 1{\overline{\text{OA’}}} - \frac 1{-8} = \frac 1{15} µ$
Donc $*\overline{\text{OA’}}*$ ≃ – 17,1 cm 2. Dans le premier cas, on a
$µ \gamma = \frac {\overline{\text{A’B’}}}{\overline{\text{AB}}}= \frac {24}{-40} = -0,6 µ$
Donc la taille de l’image est de –0,6×4 = –2,4 cm Dans le deuxième cas, on a :
$µ \gamma = \frac {\overline{\text{A’B’}}}{\overline{\text{AB}}}= \frac {-17,1}{-8} = 2,14 µ$
Donc la taille de l’image est de 2,14×4 = 8,5 cm 3. On avait trouvé 23,2 cm au lieu de 24 cm pour la position de l’image réelle, et 2,4 cm pour sa taille. On trouve bien des valeurs proches, voire très proche de ce qu’on trouve pas le calcul.
2. Calculer sa taille, dans les deux cas.
3. Comparer les valeurs calculées avec les valeurs trouvées dans l’exercice précédent.
Correction
Pareil dans le cas de l’image virtuelle : 17,6 cm de la lentille (contre 17,1 par le calcul) et une taille de 8,5 cm.
Relation du grandissement
On considère l’image réelle A’B’ d’un objet AB par une lentille de centre optique O, comme le montre le schéma ci-dessous.

En vous servant du théorème de Thalès, démontrer que :
$µ \frac {\overline{\text{A’B’}}}{\overline{\text{AB}}}= \frac {\overline{\text{OA’}}}{\overline{\text{OA}}} µ$Correction
Il suffit de voir dans quels triangles appliquer le théorème de Thalès.
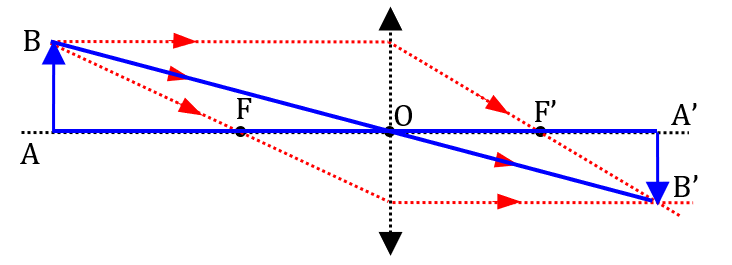
D’après le théorème de Thalès, on a : $* \dfrac {\mathrm{A’B’}}{\mathrm{AB}} = \dfrac {\mathrm{OA’}}{\mathrm{OA}}*$
La loupe
Une loupe est une lentille convergente de distance focale $*f’*$, utilisée pour former une image virtuelle.
1. Montrer, en utilisant la relation de conjugaison, que si l’objet est à une distance de la lentille $*d*$ > $*f’*$, alors l’image est réelle.
2. Montrer qu’inversement si $*d*$ < $*f’*$, alors l’image est virtuelle.
3. Quel est le signe du grandissement lorsqu’on utilise une loupe ?
4. Une lentille de focale $*f’*$ = 8 cm est utilisée comme loupe. On place un objet à 6 cm de la lentille. Quel sera le grandissement obtenu ?
Correction
1. $* \dfrac 1{\overline{\text{OA’}}} - \dfrac 1{\overline{\text{OA}}} = \dfrac 1{f’} *$ donc $* \dfrac 1{\overline{\text{OA’}}} - \dfrac 1{-d} = \dfrac 1{f’} *$ donc $* \dfrac 1{\overline{\text{OA’}}} = \dfrac 1{f’} - \dfrac 1{d} *$
Or, on sait que $*d*$ > $*f’*$ donc $*\dfrac 1d \lt \dfrac 1{f’}*$ et donc $*\dfrac 1{f’} - \dfrac 1d \gt 0 *$ et donc $*\overline{\text{OA’}}*$ est positif : l’image se forme de l’autre côté de la lentille par rapport à l’objet.
3. Ici, on forme une image virtuelle, donc $*\overline{\text{OA’}}*$ < 0 donc $* \gamma = \dfrac {\overline{\text{OA’}}}{\overline{\text{OA}}} *$ > 0.
4. On trouve $*\overline{\text{OA’}}*$ = –24 cm, donc l’image se forme à 24 cm devant la lentille.
Déterminer une focale : méthode de Silbermann
La méthode de Silbermann permet de déterminer la distance focale d’une lentille mince convergente.
On commence par placer un objet lumineux et un écran aux deux extrémités d’un banc d’optique. On place ensuite la lentille près de l’écran puis on l’éloigne jusqu’à obtenir l’image de l’objet sur l’écran : cette image est plus petite que l’objet. On éloigne un peu la lentille de l’écran puis on déplace l’écran pour retrouver l’image dont la taille a légèrement augmenté. On continue ainsi jusqu’à ce que l’image sur l’écran ait la même taille que l’objet.
1. Après avoir indiqué la nature et le sens de l’image, représenter sur un schéma l’objet et son image dans la situation finale.
2. Déterminer la position du centre optique et des foyers de la lentille.
3. Vérifier en utilisant la relation de conjugaison que la distance focale de la lentille est alors égale au quart de la distance objet-écran.
Correction
1. L’image est réelle (car on peut la recueillir sur un écran) et donc inversée. Pour faire le schéma, le mieux et de tenir compte du fait que l’objet et l’image ont la même taille.
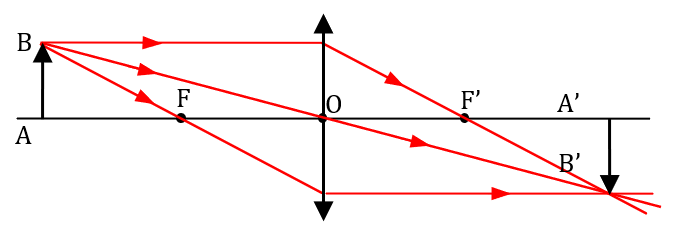
2. Par Thalès, on voit que OA’ = OA et donc la lentille se trouve à égale distance de l’objet et de l’image.
Également par Thalès, on voit que F se trouve à égale distance de O et de A, de même pour F’, qui se trouve à égale distance de O et de A’.
3. Dans la situation présente, puisque $*\overline{\text{OA}} = -\overline{\text{OA’}}*$, la relation de conjugaison devient : $µ \dfrac 1{\overline{\text{OA’}}} + \dfrac 1{\overline{\text{OA’}}} = \dfrac 1{f’} µ$ et donc $*f’ = \dfrac {\overline{\text{OA’}}}2*$. Or, comme $*\overline{\text{OA’}} = \dfrac{\overline{\text{AA’}}}2*$, on a donc bien $*f’ = \dfrac {\overline{\text{AA’}}}4*$
L’appareil photo
On modélise un appareil photographique par une lentille convergente, de distance focale 50 mm, ainsi que par un écran placé à une distance de la lentille variant entre 50 et 60 mm.
1. Faire un schéma, sans souci d’échelle, de la situation où l’appareil photo prend en photo un objet.
2. Déterminer quelles sont les distances maximale et minimale objet – lentille pour lesquelles l’appareil photo est capable d’obtenir une image nette.
3. L’appareil photo prend en photo un objet de 20 cm à une distance de 2,0 m. Quelle sera la taille de l’image formée sur le capteur ? Cette image sera-t-elle droite ou renversée ?
Correction
1. Votre schéma doit montrer que, en utilisation normale, l’objet est assez éloigné de la lentille de l’appareil photo. Il se forme une image petite et proche du foyer image.
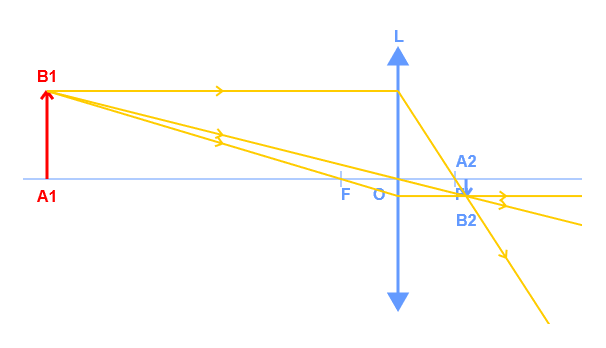
2. L’image d’un objet à l’infini se forme à la distance $*f’*$ de la lentille, soit 50 mm. Donc l’appareil photo peut prendre des photos d’objets très éloignés lorsque la lentille se trouve à 50 mm de l’écran.
Plus un objet se rapproche, plus la lentille doit s’éloigner de l’écran pour pouvoir former une image nette. La distance maximale lentille - écran est de 60 mm. On utilise la relation de conjugaison pour trouver à quelle distance objet - lentille cela correspond : $µ \dfrac 1{\overline{\text{OA}}}=\dfrac 1{\overline{\text{OA’}}}-\dfrac 1{f'} = \dfrac 1{60} - \dfrac 1{50} = -0,00333 µ$ On trouve donc que $*\overline{\text{OA}}*$ = –300 mm. L’objet le plus proche sur lequel l’appareil photo peut faire une mise au point est doit se situer à 30 cm de la lentille.
3. En appliquant la relation de conjugaison, on trouve que l’image se forme à 51,3 mm de la lentille. Le grandissement vaut donc $*\gamma*$ = -51,3÷2000 = -0,0257.
La taille de l’image sera donc de 0,0257×20 = 0,51 cm environ et elle sera renversée (car le grandissement est négatif).
Couleur de la lumière
- Choisir le modèle de la synthèse additive ou celui de la synthèse soustractive selon la situation à interpréter.
- Interpréter la couleur perçue d’un objet à partir de celle de la lumière incidente ainsi que des phénomènes d’absorption, de diffusion et de transmission.
- Prévoir le résultat de la superposition de lumières colorées et l’effet d’un ou plusieurs filtres colorés sur une lumière incidente.
Synthèse additive et synthèse soustractive
- Illustrer les notions de synthèse additive, de synthèse soustractive et de couleur des objets.
Éléments de réponses
Lumière poly– et monochromatique
Une lumière blanche est constituée d’une multitude de radiations de longueurs d’onde variant entre 380 et 780 nm. L’ensemble de ces radiations colorées constitue le spectre de la lumière blanche.
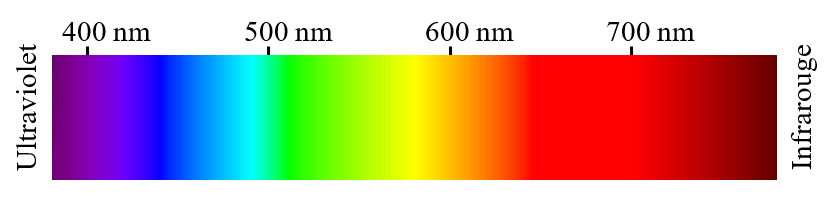
Lumière polychromatique : elle est constituée de plusieurs radiations colorées. Chaque radiation colorée est caractérisée par une longueur d’onde λ. La lumière blanche est une lumière polychromatique. La plupart des sources lumineuses sont polychromatiques.
Lumière monochromatique : elle est constituée d’une seule longueur d’onde. La lumière d’un laser est monochromatique.
Synthèse additive des couleurs
La synthèse additive des couleurs est la superpostion de lumières colorées.
En synthèse additive, les couleurs primaires sont le rouge, le vert et le bleu (RVB ou RGB en anglais).
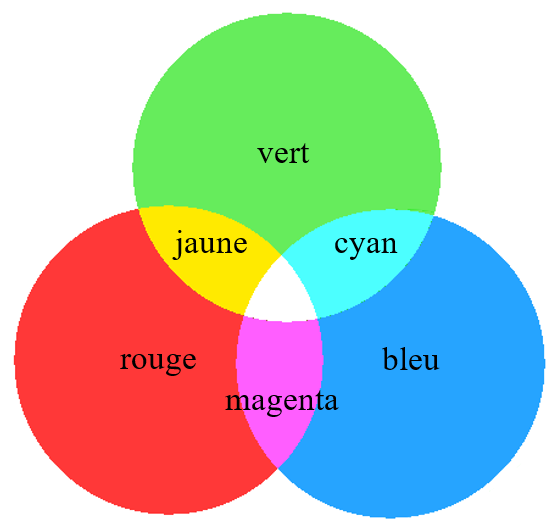
Le mélange des trois couleurs primaires produit du blanc. En choisissant judicieusement l’intensité de la lumière de chacune de ces trois couleurs, on obtient les autres couleurs de l’arc-en-ciel (dites secondaires).
Ce procédé est utilisée dans les écrans couleurs pour restituer l’ensemble des couleurs du spectre de la lumière visible.
Couleurs complémentaires
La couleur complémentaire d’une couleur primaire est celle obtenue par soustraction de cette couleur primaire à la lumière blanche.
Par exemple, la couleur complémentaire du bleu est celle obtenue par la superposition du vert et du rouge, c’est-à-dire le jaune.
Synthèse additive
Voici les spectres de quelques lumières obtenues grâce à des ampoules rouge, verte et bleue.

Pour chacun de ces spectres, indiquer (a) quelles sont les ampoules allumées et (b) la couleur perçue.
Correction
De haut en bas :
1. ampoule bleue, couleur perçue bleu
2. ampoule verte, couleur perçue verte
3. ampoule rouge, couleur perçue rouge
4. ampoule bleue + ampoule verte, couleur perçue cyan
5. ampoule bleue + ampoule rouge, couleur perçue magenta
6. ampoule verte + ampoule rouge, couleur perçue jaune
Restitution des couleurs par un écran

Chaque pixel d’un écran couleur est composé de 3 luminophores. Les luminophores sont très proches les uns des autres pour que l’œil ne puisse pas les distinguer. Pour chaque point (ou pixel) de l’image, le cerveau effectue la synthèse additive des lumières rouge, verte et bleue reçues par l’œil.
Couleurs reproduites par un écran
Un écran couleur standard est capable de restituer 256 niveaux d’intensité pour chacune des couleurs primaires (rouge, vert, bleu). Le niveau 0 est l’absence de cette couleur, le niveau 255 est le maximum possible.
1. Combien de nuances de couleurs différentes un écran est-il capable de reproduire ?
2.a. Quelle couleur va-t-il afficher si les niveaux de rouge, de vert et de bleu sont tous à 0 ?
2.b. Même question si tous ces niveaux sont à 255.
2.c. Même question si tous ces niveaux sont à 127.
3. La couleur du cadre ci-dessous est obtenu par le mélange suivant : Rouge 180 ; Vert 20 ; Bleu 80
Quelle couleur obtiendra-t-on avec le mélange : Rouge 252 ; Vert 28 ; Bleu 112 ?
Correction
1. 256×256×256 ≃ 16,8 millions de couleurs2.a. Du noir
2.b. Du blanc
2.c. Du gris
3. Les proportions des couleurs sont les mêmes, mais leur niveau a été augmenté. Il va donc s’agir de la même couleur, mais plus claire.
Couleur spectrale et couleur perçue
Couleur spectrale : c’est la couleur d’une lumière monochromatique ou quasi-monochromatique).

Couleur perçue : c’est la couleur perçue par l’œil. Une couleur perçue n’est pas forcément une couleur spectrale. Une couleur perçue est différente d’une couleur spectrale si son spectre comporte plusieurs radiations donc plusieurs couleurs (lumière polychromatique).

Couleurs des objets
Interactions lumière – matière
Diffusion
Lorsqu’un objet reçoit une lumière incidente d’une source lumineuse qui l’éclaire, celui-ci peut la diffuser. La lumière diffusée est réémise dans toutes les directions. C’est ce phénomène qui permet de voir les objets. On dit qu’ils sont alors des sources secondaires de lumière.
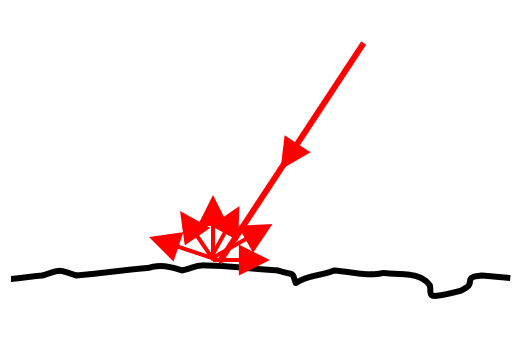
Un objet qui ne diffuserait pas de lumière serait soit totalement noir, soit tellement transparent qu’il serait invisible.
Absorption
Un objet peut absorber toute ou partie de la lumière qu’il reçoit. S’il n’absorbe que certaines couleurs, alors il aura une couleur qui sera la complémentaire des couleurs absorbées. On y reviendra dans ce paragraphe.
Exemple : un objet parfaitement bleu absorbe complètement le rouge et le vert.
Un objet qui absorbe toutes les couleurs qu’il reçoit est parfaitement noir. C’est le « corps noir » de la physique (sur lequel on reviendra au chapitre suivant).
Un objet qui n’absorbe pas la lumière qu’il reçoit est soit blanc (il diffuse toute la lumière qu’il reçoit) soit transparent (il laisse passer toute la lumière qu’il reçoit) soit réfléchissant (miroir).
Transmission
Un objet transparent est traversé par la lumière. C’est le phénomène de la transmission. Comme on l’a vu en seconde, il y a dans ce cas forcément une réflexion (rayons réfléchi et refracté, indissociables).
Réflexion
Certains objets renvoient la lumière reçue dans une direction privilégiée. Ce phénomène a été étudié en seconde.
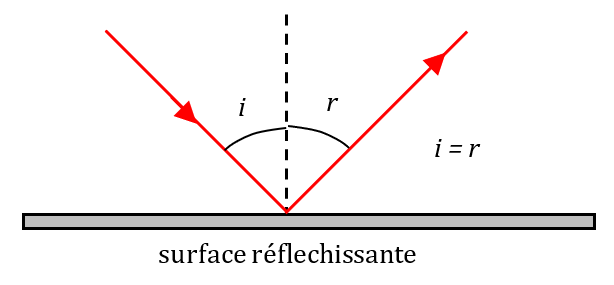
Coexistence de ces phénomènes
Ces 4 phénomènes ne s’excluent pas mutuellement. Ainsi, par exemple, une vitre rouge :
- diffuse la lumière, sinon on ne la verrait pas ;
- absorbe une partie de la lumière reçue (le vert et le bleu) ;
- transmet la lumière rouge ;
- réflechit la lumière (on peut voir son reflet dedans).
Objet coloré
✋ Pour simplifier les raisonnements qui suivent, on peut réduire la lumière blanche aux trois couleurs primaires de la synthèse additive.
La couleur d’un objet dépend de la couleur de la lumière qui l’éclaire. Lorsqu’on dit qu’un objet est jaune, on sous-entend qu’il est jaune lorsqu’il est éclairé par une lumière blanche.
Le fait qu’un objet soit jaune lorsqu’il est éclairé en lumière blanche signifie que l’objet est capable de diffuser le rouge et le vert (rouge + vert = jaune) et qu’il absorbe le bleu.
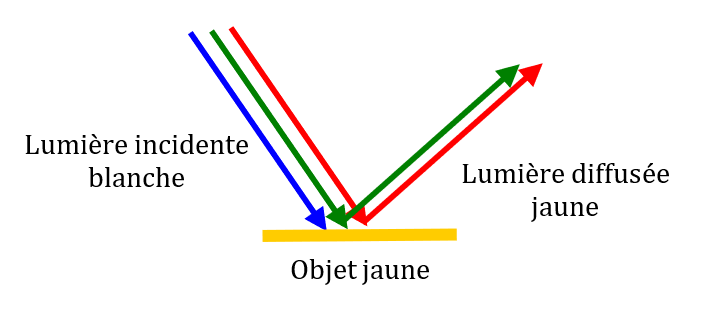
Si ce même objet est éclairé en lumière bleu, il apparaîtra noir car il absorbe le bleu. S’il est éclairé en lumière rouge, il apparaîtra rouge et s’il est éclairé en lumière verte, il apparaîtra vert.
Filtre coloré
Lorsqu’un filtre coloré idéal est traversé par une lumière, il supprime toutes les radiations qui ne correspondent pas à sa couleur. Dans la réalité, il est difficile d’obtenir un filtre idéal : un filtre rouge laissera toujours passer une petite quantité de bleu et de vert.
Exemple : un filtre coloré rouge supprime toutes les couleurs sauf le rouge.
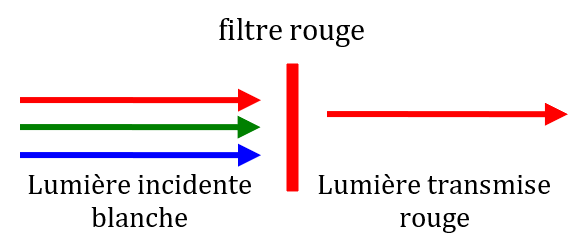
On peut également dire qu’un filtre colorée absorbe la couleur complémentaire de sa couleur. Un filtre rouge absorbe le vert et le bleu, donc absorbe le cyan, couleur complémentaire de rouge.
Synthèse soustractive
Nous avons vu qu’il est possible d’additionner des lumières rouges, vertes et bleues pour obtenir de nombreuses couleurs différentes. C’est la synthèse additive.
Mais il est également possible de partir d’une lumière blanche et de lui soustraire certaines couleurs, grâce à un filtre, pour obtenir la couleur désirée. C’est la synthèse soustractive.
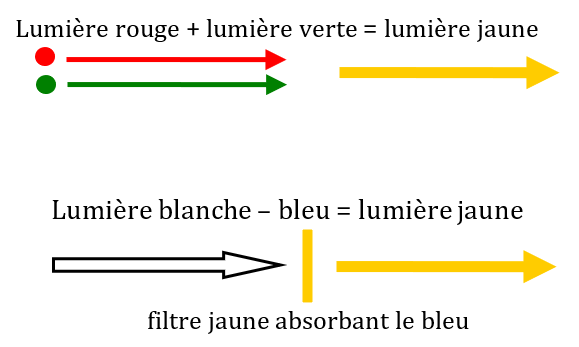
Impression en couleurs
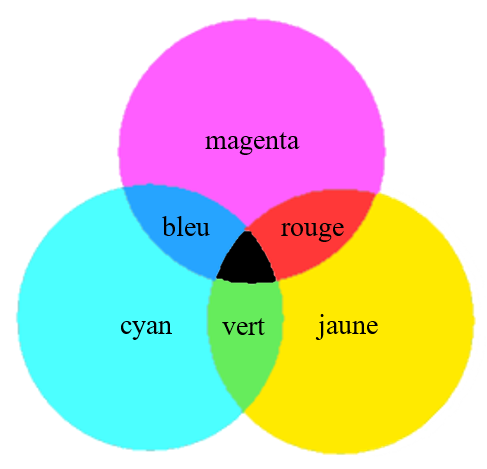
Colorer un objet ou imprimer en couleur consiste à utiliser la synthèse soustractive. Le colorant ou l’encre retire certaines couleurs à la lumière blanche incidente pour donner à l’objet ou au papier la couleur désirée.
C’est pourquoi, dans les imprimantes couleurs, les trois couleurs d’encre utilisées sont le magenta, le cyan et le jaune. Ce sont les couleurs primaires de la synthèse soustractive – celle que vous avez vue en arts plastiques.
Prévoir la couleur d’un objet selon la couleur de la lumière incidente
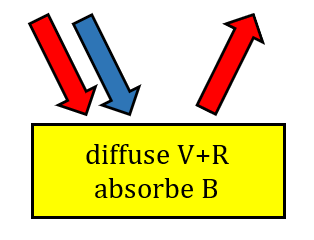
• La couleur d’un objet résulte de la synthèse additive des lumière qu’il est capable de diffuser.
Un objet cyan est capable de diffuser/transmettre le vert et le bleu. Il absorbe le rouge.
Un objet vert est capable de diffuser/transmettre le vert. Il absorbe donc le rouge et le bleu.
• La couleur d’une lumière est le résultat de la synthèse additive des couleurs qui la compose. Pour simplifier, on considèrera que la lumière blanche est composée de rouge, de vert et de bleu.
Pour prévoir quelle sera la couleur d’un objet en fonction de la couleur de la lumière incidente il faut :
- Déterminer quelles sont les couleurs qui sont présentes dans la lumière incidente, parmi le rouge, le vert et le bleu.
- Déterminer quelles sont les couleurs absorbées par l’objet, connaissance la couleur de cet objet en lumière blanche.
- En déduire quelles sont les couleurs diffusées par l’objet. La synthèse additive de ces couleurs définira la couleur de l’objet.
Exemple
Un objet jaune (donc qui absorbe le bleu) éclairé en lumière magenta (composée de bleu et de rouge) sera rouge.
Mire de couleurs
Une mire est une palette de couleurs servant à étalonner les couleurs sur un appareil photo, un écran, une imprimante, etc. Elle contient les 6 couleurs primaires et secondaires.

Donner les couleurs apparentes de cette mire lorsqu’elle est éclairée avec des lumières de différentes couleurs.
| Lumière | Couleurs |
|---|---|
| blanche | W-R-J-V-C-B-M-N |
| rouge | |
| verte | |
| bleue | |
| jaune | |
| cyan | |
| magenta |
Correction
| Lumière | Couleurs |
|---|---|
| blanche | W-R-J-V-C-B-M-N |
| rouge | R-R-R-N-N-N-R-N |
| verte | V-N-V-V-V-N-N-N |
| bleue | B-N-N-N-B-B-B-N |
| jaune | J-R-J-V-V-N-R-N |
| cyan | C-N-V-V-C-B-B-N |
| magenta | M-R-R-N-V-V-M-N |
Blanchissement du linge
En vieillissant, le linge blanc contenant des fibres naturelles comme la cellulose tend à jaunir.
1. Quelle partie du spectre est absorbée par la cellulose lorsqu’elle vieillit ?
La plupart des lessives sont enrichies en colorants. Ces agents « azurants » absorbent les rayonnements ultraviolets et réémettent dans le visible, redonnant ainsi un aspect blanc au linge.
2. Dans quelle partie du spectre visible doivent émettre les agents azurants pour redonner au linge son aspect blanc ?
3. De quel type de synthèse s’agit-il ?
Correction
1. Si la cellulose devient jaune, c’est qu’elle absorbe le bleu.2. Les agents azurants doivent compenser l’absorption du bleu due à la cellulose. Ils doivent donc réémettre dans le bleu.
3. Synthèse additive
Au concert
Lors de certains concerts, un unique projecteur (de lumière blanche) permet d’éclairer l’artiste de différentes couleurs. Pour cela, on fait appel à des filtres colorés cyan, magenta et jaune.
1. Quels filtres colorés vont être utilisés pour éclairer le musicien d’une lumière rouge? Comment devront être placés les filtres ?
2. Pourquoi utilise-t-on des filtres cyan magenta et jaune plutôt que des filtres rouge, vert et bleu ?
3. De quelle couleur sera perçue la chemise bleue de l’artiste si ce dernier est éclairé par une lumière cyan ?
4. De quelle couleur sera perçu le décor jaune s’il est éclairé par une lumière magenta ?
Correction
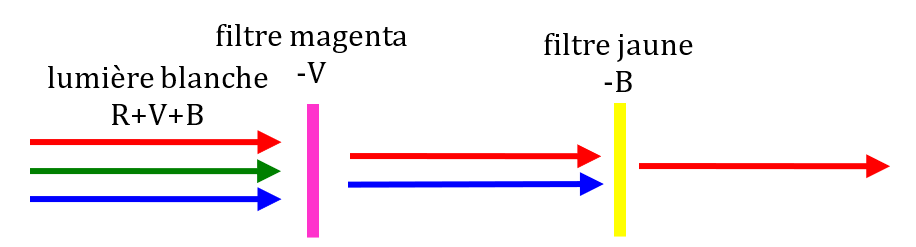
1. Pour obtenir de la lumière rouge, il faut absorber le bleu (grâce au filtre jaune) et le vert (grâce au filtre magenta).
Les filtres doivent être superposés et placés devant le projecteur. Leur ordre n’est pas important.
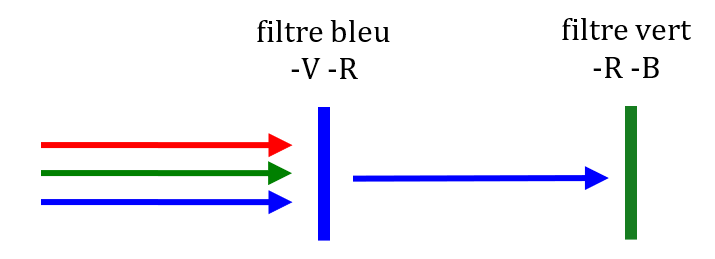
2. Les filtres cyan, magenta et jaune n’absorbent qu’une seule couleur, alors que les filtres bleu, vert et rouge en absorbent deux. On peut donc obtenir plus de couleurs différentes en utilisant les filtres cyan, magenta et jaune qu’en utilisant les filtre bleu, rouge et vert.
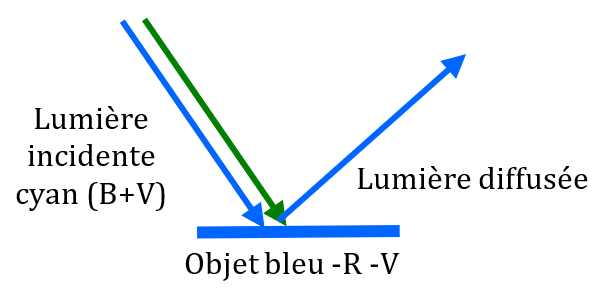
3. Le bleu absorbe le rouge et le vert. La lumière cyan contient du bleu et du vert. Le vert est absorbé par la chemise, celle-ci sera donc bleue.
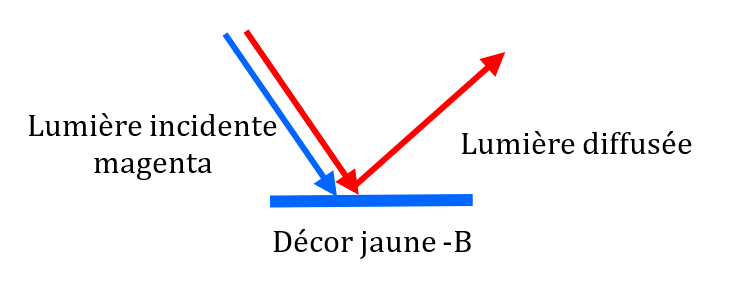
4. Le jaune absorbe le bleu. La lumière magenta contient du rouge et du bleu. Le décor sera donc perçu rouge.
Images satellites et composition colorée
Des satellites d’observation de la Terre survolent la planète en permanence pour la photographier. Contrairement à un appareil photo standard, dont le capteur est sensible au bleu, vert et rouge, les satellites d’observation de la Terre possèdent des capteurs capables d’enregistrer non seulement des longueurs d’onde correspondant au bleu, vert et rouge, mais aussi le proche infrarouge (PIR) (0,78–0,89 μm) et l’infrarouge à courte longueur d’onde (SWIR) (1,58–1,75 μm).
Végétaux et télédétection
La chlorophylle, contenue dans les feuilles des végétaux, absorbe pratiquement toutes les longueurs d’onde du spectre visible, sauf le vert qui est un peu moins absorbé.
En dehors du spectre visible, c’est très différent : presque la moitié du rayonnement PIR, qui n’est pas affecté par les pigments des feuilles, est réfléchi.
Dans le SWIR, la teneur en eau de la végétation influence fortement la signature spectrale de la végétation. Plus la teneur en eau est forte, plus la diffusion de la végétation diminue dans ces longueurs d’onde. Cette plage de longueur d’onde est très utilisée en observation de la Terre pour détecter un état de stress hydrique (manque d’eau) de la végétation.
Diffusion des différentes longueurs d’onde par différentes surfaces
| Surface | Vert | Rouge | PIR | SWIR |
|---|---|---|---|---|
| Végétation | Moyenne | Faible | Forte | Variable |
| Eau | Faible | Nulle | Nulle | Nulle |
| Sol nu et bâtiments | Moyenne | Moyenne | Faible | Faible |
| Neige | Forte | Forte | Moyenne | Faible |
Composition colorée
Un écran LCD utilise trois couleurs de base (le rouge, le vert et le bleu) pour afficher toutes les nuances colorées d’une image.
En observation de la Terre, quand il s’agit de combiner d’autres bandes spectrales, la manière de les affecter aux couleurs de base RVB définit une composition colorée. Une des compositions colorées les plus utilisées en télédétection consiste à effectuer une translation (décalage) de spectre :
- la bande proche infrarouge est représentée en rouge ;
- la bande rouge est représentée en vert ;
- la bande verte en bleu.
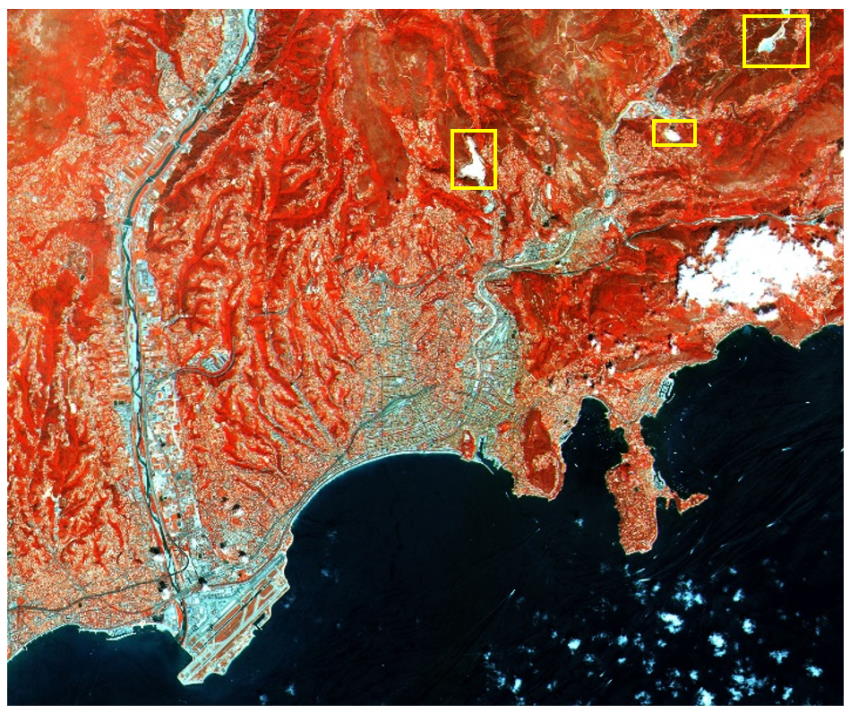
Question
1. Expliquez la couleur rouge de la végétation sur cette photo.
2. Quel type de surface a une couleur cyan ? Justifier votre réponse.
3. Justifier la couleur bleu très sombre de l’eau sur cette composition colorée.
4. Que peut-on conclure de la couleur blanche des nuages sur cette photo ?
5. Les petites zones blanches-bleutées visibles dans les montagnes sont-elles des lacs ou des zones enneigées ? Justifier.
6. Proposer une composition colorée qui permettrait de différencier les zones de végétation en état de stress hydrique des zones végétales en bonne santé.
Expliquer la couleur qu’auraient ces différentes zones dans la composition colorée que vous avez choisie.
7. Voici une image de la même zone, prise en vraies couleurs.

Expliquer quel peut être l’intérêt de travailler sur une composition colorée incluant de l’infrarouge.
Correction
1. La végétation diffuse fortement le proche IR, qui est affiché en rouge, et peu les autres couleurs.
2. Les surfaces cyan diffusent le vert et le rouge (affichés en bleu et en vert) et peu le proche IR. Il s’agit donc de bâti et de sol nu comme l’indique le document 3.
3. L’eau diffuse faiblement le vert (affiché en bleu) et ne diffuse pas le rouge et le proche IR.
4. S’ils sont blanc, c’est qu’ils diffusent fortement le vert, le rouge et le proche IR.
5. Si c’était des lacs, ils apparaîtraient noir. Ce sont donc des zones enneigées.
6. La végétation en manque d’eau diffuse plus le MIR que la végétation en bonne santé. Il faut donc afficher le canal MIR sur la composition colorée.
Composition colorée proposée : le rouge est affiché en bleu, le proche IR en vert et le SWIR en rouge.
Une végétation en manque d’eau ne diffusera pas le rouge, diffusera beaucoup le proche IR et beaucoup le SWIR. Elle apparaîtra donc en jaune (vert + rouge)
Une végétation en bonne santé ne diffusera pas le rouge, difussera beaucoup le proche IR et peu le MIR. Elle apparaîtra donc en vert.
7. Les différents types de couvert des sols sont beaucoup plus visibles sur la composition colorée que sur la photo prise dans le visible (nette différence entre la végétation et les sols nus, par exemple).
Vision des couleurs
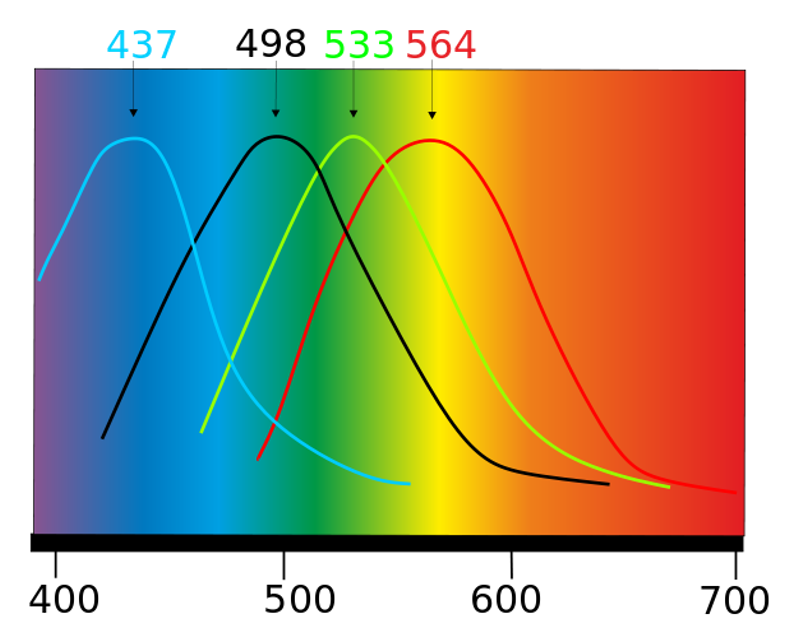
La vision des couleurs est assurée par les cônes, qui sont des photorécepteurs situés au fond de l’œil. Ceux-ci transformant le signal électromagnétique de la lumière en signal nerveux permettant la vision diurne. La vision nocturne est assurée par les bâtonnets.
L’être humain perçoit une immense variété de couleurs différentes pourtant il ne possède que trois types de cônes ayant une sensibilité plus grande à certaines radiations de longueurs d’onde comprises entre 400 et 700 nm : les cônes (B) sensibles aux radiations de courte longueur d’onde, les cônes (V) sensibles aux radiations de moyenne longueur d’onde et les cônes (R) sensibles aux radiations de grande longueur d’onde.