P8. La lumière
On sait depuis le début du XXe siècle que la lumière a une « double nature ». Elle est à la fois une onde et à la fois composée de particules appelées photons. Dans ce chapitre, le terme « lumière » sera employé comme synonyme d’onde électromagnétique. Donc je vais inclure derrière ce mot également les ultraviolets, les infrarouges et tous les autres domaines du spectre électromagnétique.
Modèle ondulatoire
- Utiliser une échelle de fréquences ou de longueurs d’onde pour identifier un domaine spectral.
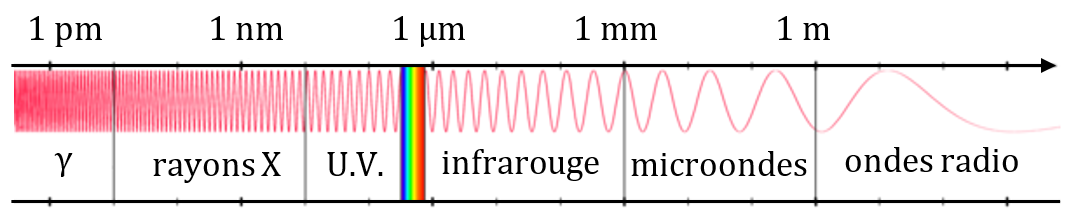
Domaines des ondes électromagnétiques
Les ondes électromagnétiques (dont la lumière fait partie) sont des perturbations du champ électromagnétique qui se déplacent.
Leur fréquence (et donc leur longueur d’onde) peuvent être extrêment variables. Cela leur donne des comportements différents lorsqu’elles rencontrent de la matière, mais leur nature fondamentale (vibration du champ électromagnétique) est toujours la même.
Longueur d’onde, célérité et fréquence
Une onde est caractérisée par une fréquence f et une longueur d’onde λ.
La lumière se déplace dans le vide à une vitesse $*c*$ = 299 792 458 m·s-1 exactement (le mètre est défini à partir de cette valeur). On prendra par la suite $*c*$ = 3,00·108 m·s-1.
Les formules vues au chapitre P6 sont, bien sûr, toujours valable pour les ondes électromagnétiques
| $*\lambda = v×T*$ |
$*\lambda*$ : longueur d’onde (m) $*v*$ : vitesse de l’onde (m·s-1) $*T*$ : période de l’onde |
D’autre par, comme la fréquence f d’un phénomène périodique vaut :
$µ f = \frac 1T µ$On peut également écrire :
| $µ \lambda = \frac vf µ$ |
$*\lambda*$ : longueur d’onde (m) $*v*$ : vitesse de l’onde (m·s-1) $*f*$ : fréquence de l’onde (Hz) |
Domaine des infrarouges
1. Donner le domaine de longueur d’onde correspondant aux infrarouges.
Le domaine des infrarouges est lui-même subdivisé en 3 sous-domaines : l’infrarouge proche ($*\lambda*$ ≤ 2 µm), l’infrarouge moyen (jusqu’à 20 µm) et l’infrarouge lointain (jusqu’à 0,1 mm ou 1 mm selon les auteurs).
2. Donner les domaines de fréquences correspondant aux trois types d’infrarouge.
Correction
Modèle corpusculaire
- Utiliser l’expression donnant l’énergie d’un photon.
- Exploiter un diagramme de niveaux d'énergie en utilisant les relations λ = c / ν et ΔE = hν.
Le photon
Il existe deux manières de décrire la lumière : soit comme une onde électromagnétique (aspect ondulatoire, que l’on vient de voir), soit comme un ensemble de photons (aspect corpusculaire – mis en évidence par Einstein en 1905).
Un photon est une particule de lumière. Sa masse est nulle (ce n’est pas une particule de matière !) et il se déplace à la vitesse de la lumière.
Un photon transporte une énergie $*E*$ qui dépend de la fréquence de l’onde électromagnétique à laquelle il est associé.
| $µ E = h \nu = \frac {hc}\lambda µ$ |
$*E*$ : énergie du photon (J) $*h*$ : constante de Planck (6,63·10-34 J·s) $*\nu*$ : fréquence de l’onde (Hz) $*c*$ : vitesse de la lumière $*\lambda*$ : longueur d’onde |
Mais rien ne ressemble plus à la lettre $*\nu*$ (fréquence) que la lettre $*v*$ (vitesse) 😅
C’est pourquoi on utilise la lettre $*c*$ (pour célérité) pour parler de la vitesse des ondes.
Unités d’énergie pour les photons
L’unité S.I. d’énergie est le joule. Mais à l’échelle du photon, cette unité est très grande ce qui oblige à manipuler de valeur en notation scientifique, peu commodes à énoncer et à écrire. On préfère utiliser une unité d’énergie adaptée à l’échelle atomique : l’électron-volt (eV).
✋ Dans les formules, il faut toujours utiliser les unités S.I ! L’eV est une unité usuelle d’énergie à l’échelle atomique.
Énergie d’un photon
1. Quelle est la longueur d’onde associée à un photon dont l’énergie vaut 1,0 eV ?
2. Quelle est l’énergie (en eV) d’un photon associé à de la lumière rouge ($*\lambda*$ = 600 nm) ?
3. L’énergie d’ionisation du fer (l’énergie qu’il faut communiquer à un atome de fer pour lui arracher un électron) vaut 7,9 eV. Quelle est la longueur d’onde maximale doit avoir la lumière pour pouvoir arracher un électron au fer ? Dans quel domaine du spectre se trouve-t-on dans ce cas ?
Correction
Quantification des niveaux d’énergie de la matière
Les électrons présents dans un atome ou un ion sont « en mouvement » autour du noyau. Ils décrivent des « trajectoires » appelées orbites. Un certain nombre d’orbites sont permises aux électrons d’un atome donné.
Un électron se trouvant sur une orbite donnée possède une certaine énergie. Plus cette orbite se trouve proche du noyau, plus cette énergie est faible.
L’énergie d’un atome ou d’un ion est la somme des énergies de chacun de ses électrons.
Sans apport d’énergie extérieure, les électrons vont occuper les orbites les plus proches possibles du noyau. On dit que l’atome se trouve dans son état fondamental, c’est-à-dire celui de plus faible énergie. C’est un état stable.
Dans certaines conditions, un atome peut gagner de l’énergie et se retrouver dans un état excité. Les états excités sont des états instables.
Un atome ne peut avoir que certains états d’énergie bien définis : on dit que l’énergie d’un atome est quantifié. On peut représenter les différents niveaux d’énergie que peut prendre un atome (ou un ion, ou une molécule) par un diagramme tel que celui ci-dessous :
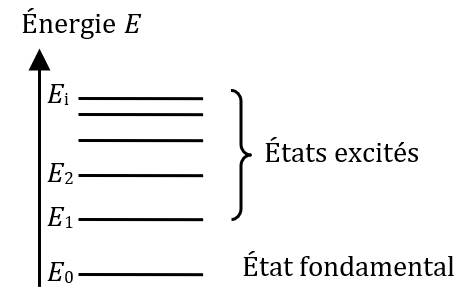
Interaction lumière - matière
Un atome peut absorber un photon (grain de lumière) si l’énergie du photon lui permet d’atteindre exactement l’énergie d’un autre état.
Un atome excité va très rapidement perdre de l’énergie pour revenir à son état fondamental. Ce faisant, il va émettre un photon chaque fois qu’il change d’état. L’énergie du photon émis correspond exactement à l’énergie perdue par l’atome.
Il émettra donc soit un photon dont l’énergie est $*E_3 - E_1*$ soit un photon dont l’énergie est $* E_3 - E_2 *$ puis un autre dont l’énergie est $* E_2 - E_1 *$.
Interprétation des spectres de raies
Une raie d’émission correspond à la désexcitation d’un atome avec émission d’un photon d’énergie $*E = E_i - E_f*$
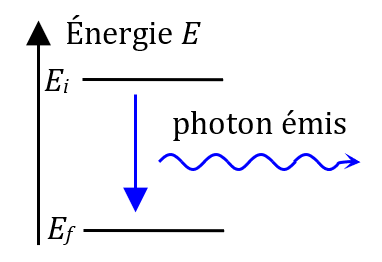
Une raie d’absorption correspond à l’absorption d’un photon d’énergie $*E = E_f - E_i*$

Raies de l’atome d’hydrogène
Il est préférable de faire cet exercice avec Excel.
Les différents niveaux d’énergie $*E_1*$, $*E_2*$, $*E_3*$, etc. de l’atome d’hydrogène sont donnés par la formule : $µ E_n = - \frac {13,6}{n^2} µ$ où $*E_n*$ s’exprime en électron-volt. Le niveau le plus haut, $*E_{ion}*$ = 0, correspond à l’ionisation de l’atome.
1. Calculer les énergies en électron-volt des niveaux $*n*$ = 1 à $*n*$ = 7. Placer ces niveaux approximativement sur un graphique.
2.a. Calculer les longueurs d’onde minimale et maximale associées aux transition d’un état d’énergie vers le niveau fondamental (raies de Lymann). Exprimer le résultat en nm.
2.b. Ces rayonnements sont-ils visibles ?
3. Mêmes questions pour les transitions vers le niveau 2.
Correction
Raies du sodium
Il est préférable de faire cet exercice avec Excel.
Les lampes à vapeur de sodium utilisées pour l’éclairage public émettent une lumière jaune-orange.
On donne les énergies des niveaux suivants du sodium :
- niveau 3s : 0 eV ;
- niveau 3p 1/2 : 2,105 eV ;
- niveau 3p 3/2 : 2,107 eV ;
- niveau 4d : 4,293 eV
1. Représenter les niveaux du sodium sur un diagramme énergétique sans se soucier de l’échelle.
2. Déterminer en eV l’énergie des photons associés à toutes les transitions possibles entre les états de ces niveaux d’énergie.
3. Une lampe à vapeur de sodium émet un doublet (c’est-à-dire deux raies de longueurs d’onde très proches) orange et un autre doublet vert-jaune. Déterminer les longueurs d’onde dans le vide de ces quatre radiations.