C1. La matière
Qu’est-ce que la matière ? Comment peut-on la transformer ? La physique et la chimie répondent à ces très vastes questions.
La matière est quelque chose qui possède à la fois un volume et une masse. C’est cette propriété qui la caractérise.
Les atomes
- Notions d’atomes
- Constituants de l’atome, structure du noyau atomique
Qu’est-ce qu’un atome ?
Un peu d’histoire
À l’époque de la Grèce antique, les savants avaient deux hypothèses concernant la matière :
- La matière est une sorte de « pâte » que l’on peut découper à l’infini. Il n’existe pas de quantité minimale de matière.
- La matière est constitué de « grains minuscules ». La quantité minimale de matière est un de ces « grains » minuscules. C’est la théorie atomiste attribuée à Démocrite.
Bien plus tard, à la fin du XIXe siècle puis au début du XXe siècle, les savants auront la certitude que c’est l’hypothèse atomiste qui est la bonne (même si de nombreux faits découverts au XVIIe siècle et plus tard pointaient vers cette hypothèse).

(460 av. J.-C. – 370 av. J.-C.)
La matière ordinaire est constituée d’atomes. Vous pouvez vous imaginer un atome comme une toute petite bille, très dure, dont la taille varie selon le type d’atome (nous reviendrons sur le sujet un peu plus tard).
Le mot atome vient du grec átomos, qui veut dire « qu’on ne peut pas couper ».
Taille d’un atome
Les atomes sont tellement petits qu’il est difficile de se représenter leur taille. Mais on va quand-même essayer de le faire. 😊
Imaginons une petite boule de fer de la taille d’un grain de sable, c’est-à-dire de 0,5 mm de diamètre. Imaginons que vous vouliez compter les atomes de fer qui le constituent, et que vous soyez capable de compter très très vite (1000 atomes par seconde).
Pour arriver à tous les compter, il vous faudrait presque 180 millions d’années. 😅
Constitution d’un atome
De quoi est fait un atome ?

Le noyau d’un atome est lui-même constitué de deux types de particules : les protons et les neutrons. Ces deux types de particules sont appelées des nucléons.
Les électrons sont chargés négativement. Ils sont attirés par le noyau qui est chargé positivement. En fait, dans le noyau, ce sont les protons qui sont chargés positivement, les neutrons, comme leur nom l’indique, ne sont pas chargés – on dit qu’ils sont neutres.
Vous le savez, (ou pas ? 😏) les charges électriques opposées s’attirent : les électrons ⊖ sont attirés par les protons ⊕ du noyau.
Électroneutralité de l’atome
La charge ⊕ de chaque proton contenu dans le noyau est compensée par la charge ⊖ de chaque électron autour du noyau. Et comme dans un atome, il y a autant d’électrons que de protons, ça signifie qu’un atome est électriquement neutre.
Masse et taille du noyau atomique
Les électrons sont presque 2 000 fois plus légers que les nucléons (c’est-à-dire que les protons et les neutrons). Les protons et les neutrons ont approximativement la même masse. Ça veut dire que quasiment toute la masse d’un atome est concentrée dans son noyau.
Mais ce n’est pas tout. Le noyau d’un atome est aussi beaucoup beaucoup plus petit que l’atome lui-même. Il est en fait environ 100 000 fois plus petit que l’atome (qui est déjà très très petit 😏).
Synthèse du paragraphe
Dans le paragraphe que vous venez de lire, il y a pas mal d’informations. Vous allez en faire une synthèse en y faisant apparaître un schéma.
Correction
Voici une proposition de correction. Cette synthèse fait apparaître le minimum qui doit figurer sur la vôtre.
Les éléments chimiques
- Associer leurs symboles aux éléments à l’aide de la classification périodique
- Comparer les ressources terrestres de certains éléments
- Les éléments sur Terre et dans l’Univers
Comment est défini un élément chimique ?
Les propriétés chimiques d’un atome dépendent du nombre d’électrons qu’il possède, et donc aussi du nombre de protons qu’il a dans son noyau. Ce nombre de protons est appelé « numéro atomique » et est noté $*Z*$.
Les atomes sont classés en « éléments » chimiques. L’appartenance à un type d’élément chimique dépend seulement du nombre de protons que contient l’atome. Par exemple, tous les atomes qui possèdent un proton (et donc un électron) sont des atomes d’hydrogène.
Chaque élément chimique a un symbole, constitué d’une lettre majuscule (H, C, O par exemple) ou bien d’une lettre majuscule et d’une lettre minuscule (Ag, Cu, Li par exemple).
Le tableau périodique
Le tableau périodique des éléments montrent tous les éléments chimiques connus, en leur associant certaines informations (dont leur numéro atomique $*Z*$).
Le tableau périodique présente les différents éléments chimiques classés par numéro atomique croissant. Il se lit comme un texte, ligne par ligne de gauche à droite.
Lire le tableau périodique
1. Le lithium a pour numéro atomique $*Z*$ = 3. Quel est son symbole chimique ? Combien de protons comporte le noyau d’un atome de lithium ? Combien d’électrons contient l’atome de lithium ?
2. Donner le symbole chimique, le numéro atomique et le nombre d’électrons de l’atome de silicium ?
3. L’élément chimique le plus « lourd » que l’on puisse trouver naturellement sur Terre est celui dont le numéro atomique $*Z*$ vaut 92. Quel est cet élément ? Combien d’électrons a-t-il ?
Correction
1. Symbole chimique : Li ; 3 protons et 3 électrons.
2. Symbole chimique : Numéro atomique $*Z*$ = 14 ; 14 électrons.
3. Il s’agit de l’uranium. Son numéro atomique est $*Z*$ = 92. Il a donc 92 protons et donc 92 électrons.
Espèces chimiques
- Notions de molécules, ions
- Espèce chimique
- Interpréter une formule chimique en termes atomiques : dioxygène, dihydrogène, diazote, eau, dioxyde de carbone, méthane, protoxyde d’azote
Molécules
La plupart des atomes peuvent former des liaisons avec d’autres atomes. Ils forment des liaisons parce qu’ils sont chimiquement plus stables que lorsqu’ils sont seuls.
Le nombre de liaisons que peut former un atome dépend de l’élément auquel il appartient. Par exemple, tous les atomes d’hydrogène ne peuvent former qu’une seule liaison, alors que les atomes de carbone peuvent en former quatre.
Par exemple, si 4 atomes d’hydrogène se lient à un atome de carbone, on obtient une molécule – très simple – qu’on appelle le méthane (il s’agit du gaz « naturel » qui est utilisé comme carburant par certains véhicules ou certaines centrales électriques).
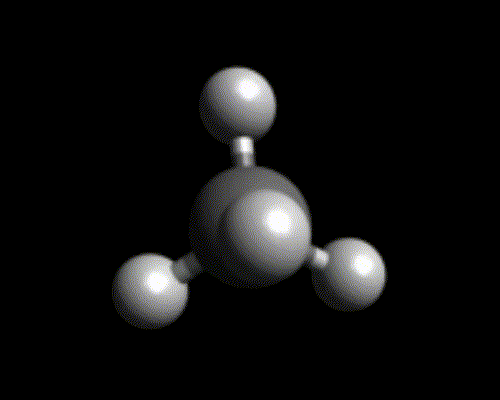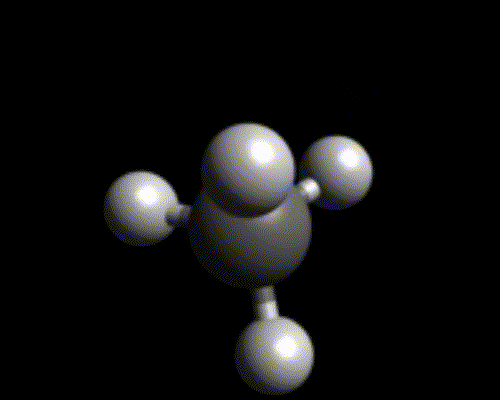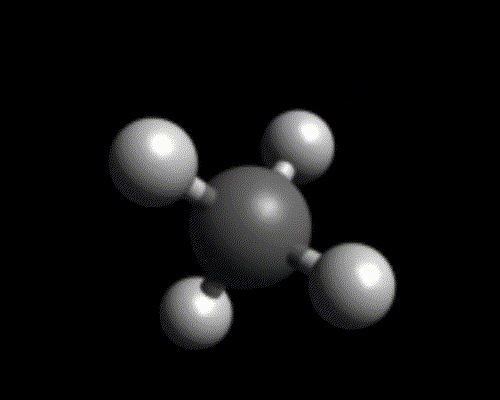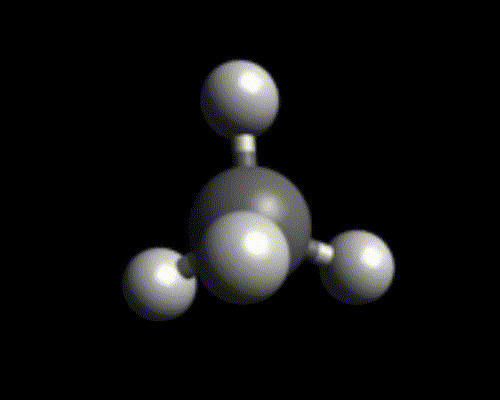
Ions
Un ion porte toujours, par définition, une charge électrique. Par exemple, l’ion chlorure $*\ce{Cl^-}*$ est un atome de chlore $*\ce{Cl}*$ qui a un électron de trop. L’ion sodium $*\ce{Na^+}*$ est un atome de sodium $*\ce{Na}*$ qui a perdu un électron.
Il existe aussi des ions polyatomiques, c’est-à-dire composés de plusieurs atomes, comme par exemple l’ion ammonium $*\ce{NH4^+}*$ qui est composé de 4 atomes d’hydrogène, d’un atome d’azote ($*\ce{N}*$) et à qui il manque un électrons.
En résumé
• Un atome est électriquement neutre. Sinon, il s’agit d’un ion monoatomique
• Une molécule est électriquement neutre. Sinon, il s’agit d’un ion polyatomique.
Espèce chimique
Le terme espèce chimique désigne un ensemble d’entités chimiques identiques : chaque entité est soit un atome (espèce chimique atomique) soit un groupe d’atomes liés qui peut, selon sa charge électrique, être une molécule ou un ion.
On désigne une espèce chimique par le nom de la molécule, de l’ion ou de l’atome qui la constitue.
Quelques exemples
- l’espèce chimique argon est une espèce atomique ; sa formule chimique est $*\ce{Ar}*$ ;
- l’espèce chimique diazote est une espèce moléculaire ; la formule chimique de cette molécule diatomique est $*\ce{N2}*$ ;
- l’espèce chimique chlorure est une espèce ionique monoatomique ; sa formule chimique est $*\ce{Cl−}*$ ;
- l’espèce chimique nitrate est une espèce ionique polyatomique ; la formule chimique de cet ion polyatomique est $*\ce{NO3^−}*$ ;
Par contre, le beurre n’est pas une espèce chimique, car il n’existe pas de molécules de beurre (le beurre est composé d’un très grand nombres d’espèces chimiques différentes – comme la plupart de ce qui nous entoure).
Une espèce chimique a donc une formule chimique, qui décrit quels sont les atomes qui la composent et en quelle quantité.
Quelques espèce chimiques à connaître
| Nom | Formule | Constitution |
| dioxygène | $*\ce{O2}*$ | 2 atomes d’oxygène $*\ce{O}*$ |
| dihydrogène | $*\ce{H2}*$ | 2 atomes d’hydrogène $*\ce{H}*$ |
| diazote | $*\ce{N2}*$ | 2 atomes d’azote $*\ce{N}*$ |
| eau | $*\ce{H2O}*$ | 2 $*\ce{H}*$ et un $*\ce{O}*$ |
| dioxyde de carbone | $*\ce{CO2}*$ | un $*\ce{C}*$ et 2 $*\ce{O}*$ |
| méthane | $*\ce{CH4}*$ | un $*\ce{C}*$ et 4 $*\ce{H}*$ |
| protoxyde d’azote | $*\ce{N2O}*$ | 2 $*\ce{N}*$ et un $*\ce{O}*$ |
Classer des espèces chimiques
Parmi les espèces ci-dessous, regrouper les espèces qui sont des ions, celles qui sont des atomes et celles qui sont des molécules.
$*\ce{CO}*$ $*\ce{CO3^{2-}}*$ $*\ce{Co}*$ $*\ce{Co^{2+}}*$ $*\ce{HCl}*$ $*\ce{CH3CO2H}*$ $*\ce{Ne}*$ $*\ce{I_2}*$
Correction
Ions : $*\ce{CO3^{2-}}*$ ; $*\ce{Co^{2+}}*$
Atomes : $*\ce{Co}*$ ; $*\ce{Ne}*$
Molécules : $*\ce{CO}*$ ; $*\ce{HCl}*$ ; $*\ce{CH3CO2H}*$ ; $*\ce{I_2}*$
Lire une formule chimique
Donner la composition des molécules des espèces chimiques suivantes :
$*\ce{C12H22O11}*$ $*\ce{CHCl3}*$ $*\ce{NO2}*$ $*\ce{O3}*$
Correction
$*\ce{C12H22O11}*$ : 12 atomes de carbone, 22 atomes d’hydrogène et 11 atomes d’oxygène.
$*\ce{CHCl3}*$ : 1 atome de carbone, 1 atome d’hydrogène et 3 atomes de chlore.
$*\ce{NO2}*$ : 1 atome d’azote et 2 atomes d’oxygène.
$*\ce{O3}*$ : 3 atomes d’oxygène.
Masse volumique
- Masse volumique : relation $*m = \rho·V*$, influence de la température.
- Proposer et mettre en œuvre un protocole expérimental pour déterminer une masse volumique d’un liquide ou d’un solide.
- Exploiter des mesures de masse volumique pour différencier des espèces chimiques.
Comme je vous le disais dans l’introduction, ce qui caractérise la matière, c’est qu’elle a une masse et un volume. Quelque chose qui n’a pas de masse (par exemple la lumière, le son…) n’est pas de la matière.
Pour mesurer une masse, rien de plus facile. Vous savez le faire depuis longtemps, il suffit de disposer d’une balance.
Volume d’un liquide
La mesure du volume d’un liquide nécessite de faire usage d’un récipient capable d’indiquer quel volume de liquide il contient. L’éprouvette graduée permet de faire cette mesure avec une précision relativement bonne.

Volume d’un solide
Le cas des solides est plus compliqué. Si le solide a une forme géométrique régulière (par exemple, un cube, une sphère), il suffit de mesurer ses dimensions puis de calculer son volume à l’aide de formule géométrique.
Mais la plupart du temps, ça ne sera pas le cas… 😅
TP Mesurer le volume d’un solide 1
Votre professeur va vous donner un objet qui a une forme complexe. Votre mission : déterminer son volume aussi précisément que possible.
Pour cela, vous disposez du matériel de laboratoire que vous souhaitez.
Petit indice : réflechissez à ce qu’il se passe lorsque vous plongez un solide dans l’eau, en supposant que ce solide ne flotte pas, ce qui sera le cas de l’objet que je vous donnerai.
Déplacement d’eau
On peut mesurer le volume d’un solide en mesurant l’augmentation du volume du liquide dans lequel il est entièrement plongé (s’il flotte, ça ne marche pas… ou pas aussi bien).
Pour cela, il suffit de prendre une éprouvette graduée, d’y verser de l’eau (sans la remplir complètement), puis d’y introduire le solide. Le niveau de l’eau va monter car l’objet a déplacé un volume d’eau égal au sien.
On regarde ensuite quelle est l’augmentation du volume de l’eau qui contient l’objet. Cette augmentation de volume correspond exactement au volume de l’objet.
Je n’ai jamais dit que cette méthode pouvait s’appliquer à tous les objets. 😊
Elle a ses limites. D’une part il y a les problèmes que vous venez de soulever, mais il y en a d’autres : si l’objet a un faible volume, l’augmentation de volume de l’eau sera faible aussi et elle ne pourra pas être déterminée précisemment.
Méthode d’Archimède
À propos d’Archimède
Un savant grec très astucieux, nommé Archimède, a eu une idée de génie pour pouvoir mesurer avec une très grande précision le volume d’un solide quelconque.
Selon Vitruve, le mot Eurêka (signifiant « J’ai trouvé ! ») a été prononcé par Archimède en courant nu à travers les rues de Syracuse car il venait de trouver la solution à un problème posé par Hiéron II, tyran de cette ville.
Hiéron avait fourni à un orfèvre une certaine quantité d’or pour fabriquer une couronne. Afin d’être sûr que l’orfèvre ne l’avait pas dupé en substituant de l’argent (métal moins cher) à une partie de l’or, Hiéron demanda à Archimède de déterminer si cette couronne était effectivement constituée d’or pur. C’est dans sa baignoire, alors qu’il cherchait depuis longtemps, qu’Archimède trouva la solution et sortit de chez lui en prononçant la célèbre phrase. Il lui suffisait de comparer sa masse volumique à celle de l’or massif.
On reviendra plus tard dans ce paragraphe sur la notion de masse volumique. Ce qui nous intéresse pour l’instant, c’est de comprendre comment Archimède a réussi à mesurer très précisemment le volume de cette couronne.
TP Mesurer le volume d’un solide 2
Votre professeur va vous donner un objet qui a une forme complexe. Votre mission : déterminer son volume aussi précisément que possible en utilisant la méthode d’Archimède.
Matériel
- Le solide dont il faut déterminer le volume ;
- Une balance ;
- De la ficelle ;
- Un récipient ;
- Un pied et une pince.
Expérience
- Attacher l’objet à la ficelle puis attacher cette ficelle à la pince de manière à ce que celui-ci soit suspendu à la ficelle.
- Mettez de l’eau dans le récipient fourni (remplissez-le environ au ⅔).
- Mettez le récipient sur une balance puis tarer la balance.
- Faite descendre l’objet dans l’eau jusqu’à ce qu’il soit complètement immergé.
- Lisez la valeur affichée par la balance.
Lorsqu’on plonge un objet dans de l’eau sans que celui-ci ne flotte ou ne touche le fond du récipient, l’augmentation, en gramme, de la masse de l’ensemble {eau + objet immergé} est exactement égale au volume de l’objet en mL. Cette manière de faire nous permet d’être très précis lors de la détermination du volume d’un objet.
Vous aurez une explication plus détaillée de ce phénomène au lycée.
Déterminer une masse volumique
La masse volumique d’un objet, que l’on appelle parfois densité (bien que ce terme soit légèrement différent – nous y reviendrons peut-être plus tard), se calcule grâce à la relation suivante :
| $* \rho = \dfrac mV *$ |
$*\rho*$ : masse volumique (rhô) $*m*$ : masse $*V*$ : volume |
L’unité S.I (système international) de la masse volumique est le kg·m-3. Mais bien souvent, on utilise également le g·mL-1. Tout dépend dans quelles unités vous exprimez la masse et le volume de votre objet.
Il peut être intéressant de se souvenir que 1 g·mL-1 = 1 kg·L-1 = 1 t·m-3.
Masse volumique & matériaux
Un ingénieur souhaite déterminer la masse volumique de la pierre qu’il va utiliser pour une construction. Il prend un échantillon de cette pierre et mesure son volume et sa masse. Il trouve un volume $*V*$ = 260 mL et une masse de 842 g.
1. Quelle est la masse volumique de cette pierre ?
Sur son chantier, l’ingénieur dispose d’un camion benne pouvant transporter jusqu’à 10 t (tonnes).
2. Quel volume de pierre peut transporter ce camion ? Exprimer ce volume en m3.
Correction
1. Masse volumique $*\rho = \frac mV*$ = 842÷260 = 3,24 g·mL-1
2. Il faut d’abord convertir la masse en g : 10 t = 10·103 kg = 10·106 g.
Puis on calcule le volume de pierre transportable : $*V = \frac m\rho = *$ 10·106÷3,24 = 3,09·106 mL.
Ensuite, on convertit ce volume en m3 : 1 m3 = 103 L = 106 mL.
Donc $*V*$ = 3,09·106÷106 = 3,09 m3.
On peut également remarquer que 3,24 g·mL-1 = 3,24 t·m-3. Du coup, le calcul peut être plus direct : $*V = \frac m\rho = *$ = 10÷3,24 = 3,09 m3.
TP Identifier des métaux
Vous diposez d’un échantillon de 3 métaux différents : fer, zinc et aluminium.
Identifier chaque métal en déterminant expérimentalement la masse volumique des échantillons et en la comparant aux données ci-dessous.
Masses volumiques
- fer : 7,87 g·mL-1
- zinc : 7,13 g·mL-1
- aluminium : 2,70 g·mL-1
Éléments de réponses
Dans certaines situations, la mesure précise d’une masse volumique permet de distinguer certaines espèces chimiques ou la composition de certains mélanges. Par exemple, il est possible de distinguer deux métaux par leur masse volumique. Ou encore, il est possible de vérifier si un morceau d’or est pur ($*\rho_\mathrm{or}*$ = 19,3 g·cm-3) ou bien allié avec de l’argent (l’or à 18 carats – un alliage comptant 75 % d’or et 25 % d’argent – a une masse volumique de 16,5 g·cm-3).
Masses volumiques extrêmes
1. Le métal le plus dense – c’est-à-dire dont la masse volumique est la plus élevée – est l’osmium (symbole chimique : Os). Sa masse volumique est de 22,6 g·mL-1. Calculer la masse d’un cube d’osmium de 10 cm de côté.
2. L’aérographite détient le record du monde du solide le le moins dense depuis 2012. Sa masse volumique est de 0,2 mg·mL-1. Calculer la masse d’un morceau d’aérographite de la taille d’une salle de classe (10 m × 6 m × 3 m).
3. Les étoiles à neutrons sont des restes d’étoiles mortes qui ne sont pas composées de matière ordinaire, c’est-à-dire faite d’atomes. Elles sont composées de neutrons. Elles ont une masse volumique incroyablement élevée de 1017 kg·m-3. ! Quelle serait la masse d’une bille de 1 mm de diamètre faite de cette matière ? Comparer cette masse à celle de la Tour Eiffel (environ 10.000 t).
Correction
1. Volume du cube : $*V*$ = 10×10×10 = 1000 cm3 = 1000 mL.
$*m = \rho·V *$ = 22,6 g·mL-1×1000 mL = 22600 g soit 22,6 kg.
2. Volume : $*V*$ = 10×6×3 = 180 m3 soit 180·106 mL.
$*m = \rho·V*$ = 0,2 mg·mL-1×180·106 mL = 36·106 mg = 36 kg.
3. Le rayon de la bille vaut 0,5 mm soit 5·10-4 m.
Volume : $*V = \frac 43 \pi r^3 =*$ 5,24·10-10 m3.
Masse : $*m = \rho·V*$ = 1017 kg·m-3×5,24·10-10 = 5,24·107 kg, soit 52,4 t (tonnes)
Cette bille pèse plus que 5 fois la Tour Eiffel.
Masse volumique et température
Lorsque la température d’un matériau s’élève, il se dilate : son volume augmente. Mais sa masse ne change pas.
Inversement, lorsqu’on refroidit un matériau, il se contracte : son volume diminue.
Cela signifie que la masse volumique d’un matériau dépend de sa température. Elle diminue légèrement lorsque la température s’élève et augmente lorsque sa température diminue.
Cette variation n’est pas très importante pour les liquides et les solides (mais elle l’est pour les gaz). Pour vous donner une idée, voici un tableau montrant la masse volumique de l’eau à différentes températures.
| Température (°C) | $*\rho*$ (g·mL-1) |
|---|---|
| 15 | 0,9991 |
| 25 | 0,9970 |
| 40 | 0,9922 |
| 70 | 0,9778 |
Montée du niveau des océans
Le réchauffement climatique est responsable d’une élévation du niveau des océans. Contrairement à ce qu’on peut croire, la fonte des glaces n’est pas la seule raison de cette élévation. La dilatation de l’eau des océans, à cause de l’élévation de la température, joue également un rôle non négligeable. Je vous propose un petit exercice à ce sujet pour vous en convaincre… 😊
Montée des eaux
1. En vous aidant des données du paragraphe ci-dessous, calculer la masse d’un litre d’eau à 15 °C.
2. Calculer le volume de la masse d’eau trouvée à la question précédente, à une température de 25 °C.
3. Exprimer cette variation de volume en pourcentage.
Cette variation de volume ne paraît pas très grande. Mais il ne faut pas oublier que les océans ont une profondeur moyenne de 4000 mètres. Pour mieux se rendre compte des effets de la dilatation sur une telle masse d’eau, imaginons un parallèlépipède de 10 cm de large, 10 cm de profondeur et 4000 m de haut, rempli d’eau à 15 °C ! Dans ce parallèlépipède, l’eau ne peut pas s’étendre sur les côtés : elle ne peut que monter.
4.a. Calculer la variation du volume de l’eau contenu dans ce parallèlépipède lorsque l’eau qu’il contient atteint une température de 25 °C.
4.b. En déduire l’élévation du niveau de l’eau dans ce parallèlépipède, sachant que seule sa hauteur peut varier.
4.c. Conclure quant au rôle de la dilatation de l’eau dans l’élévation du niveau des océans.
Correction
1. $*m = \rho·V =*$ 0,9991 g·mL-1 ×1000 mL = 999,1 g
2. $*V = \frac m\rho*$ = 999,1 g ÷ 0,9970 g·mL-1 = 1002,1 mL
3. Le volume a augmenté de 2,1 mL. 1000 mL correspondent à 100 %, donc 2,1 mL correspondent à 2,1×100÷1000 = 0,21 %
4.a. Un petit schéma permet de mieux visualiser le problème. C’est important, en physique, de faire des schémas !
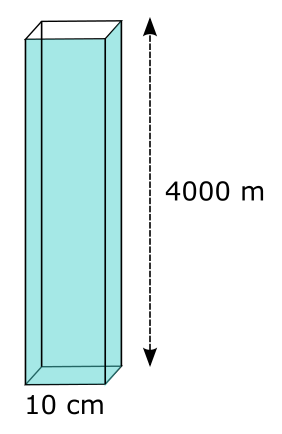
Le volume de cette colonne, en m3 est de $*V*$ = 0,1×0,1×4000 = 40 m3.
Lorsque l’eau passe de 15 °C à 25 °C, la variation de volume est de 0,21 %, c’est-à-dire 40×0,21÷100 = 0,084 m3.
4.b. Cette variation de volume $*\Delta V*$ est représentée sur le schéma ci-dessous en bleu plus foncée. On cherche à calculer la hauteur $*h*$ qui figure sur le schéma.
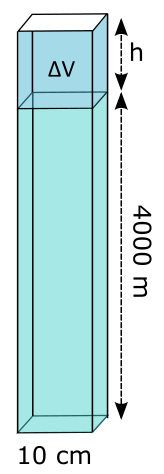
$*\Delta V = 0,1×0,1×h*$ donc $*h*$ = 8,4 m !.
4.c. On voit que la seule dilatation peut produire une grande élévation du niveau de la mer. Bien sûr, les océans ne vont pas se réchauffer de 10 °C, mais on voit que, même si l’élévation de température est faible, il est facile de gagner quelques centimètres voire quelques dizaines de centimètres.