C2. Dosage conductimétrique par étalonnage
Nous avons déjà vu l’année dernière des exemples de dosage. Doser, en chimie, c’est déterminer une concentration ou une quantité de matière d’une substance donnée présente dans un échantillon. C’est une des « activités » fondamentales de la chimie. Il existe plein de techniques de dosage en chimie. Une famille de techniques de dosage, appelés « dosage par étalonnage » consiste à comparer une grandeur physique mesurable de l’échantillon (par exemple, la conductivité – dont nous parlerons dans ce chapitre – ou l’absorbance, vue en première, mais il y en a d’autres aussi) à une courbe d’étalonnage, c’est-à-dire un graphique qui montre l’évolution de cette grandeur physique mesurée en fonction de la concentration de l’espèce chimique dosée.
Mesurer une conductivité
L’eau pure ne conduit pas le courant, car elle ne contient pas d’ions (bon, ce n’est pas rigoureusement vrai, mais on en reparlera dans un chapitre ultérieur 😅). Par contre, dès qu’une solution aqueuse contient des ions, elle est conductrice, du fait que ces ions peuvent se déplacer – rappelez-vous : un courant, c’est un mouvement de charge.
Vous vous doutez bien que plus la concentration des ions est importante, plus la capacité de la solution à conduire le courant est forte. C’est donc le moment d’introduire deux notions liées, mais distinctes : la conductance d’une solution et sa conductivité.
Conductance
La conductance d’un « truc » c’est l’inverse (au sens mathématique) de sa résistance. Par exemple, un résistor de résistance 10 Ω a une conductance $*G*$ de 0,1 siemens (S). Jusque-là, pas de problème.
Le problème, c’est que la conductance en elle-même n’est pas une grandeur très intéressante, car elle dépend de beaucoup de facteurs. Vous savez certainement que le cuivre est un très bon conducteur. Meilleur que le fer par exemple. Alors est-ce que ça veut dire qu’un fil de cuivre à une conductance plus élevée qu’un fil de fer ? Eh bien pas forcément. Ça dépend du diamètre et de la longueur de chaque fil. Un fil de fer épais et court pourra avoir une meilleure conductance qu’un fil de cuivre fin et long, tout simplement parce que les électrons ont plus de « place » pour circuler si le fil est épais. De plus, ils rencontrent une résistance plus faible si le fil est court parce qu’ils ont moins de chemin à parcourir.
Par contre, si on compare deux fils, l’un en cuivre et l’autre en fer, strictement identiques en diamètre et en longueur, alors oui, le fil de cuivre aura une meilleure conductance que le fil de fer. Même principe pour une solution aqueuse contenant des ions.
Et pourtant, il y en a un. Voyons comment fonctionne un conductimètre, l’appareil qui mesure la conductivité d’une solution (on va voir juste après ce qu’est la conductivité). Un conductimètre, c’est un ohmmètre relié à une cellule conductimétrique.
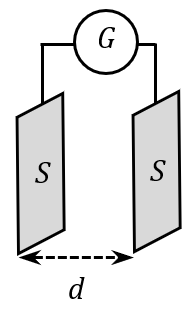
Une cellule conductimétrique est constituée de deux plaques métalliques face à face, de surface $*S*$ et distantes de $*d*$. Le conductimètre mesure la conductance qu’il y a entre les deux plaques. Mais cette conductance ne dépend pas que de la solution. Elle dépend aussi de la surface des plaques (qui est l’équivalent du diamètre des fils électriques) et de la distance entre les plaques (qui est l’équivalent de la longueur du fil).
Conductivité
La conductivité $*\sigma*$ d’une solution, c’est la partie de la conductance $*G*$ qui ne dépend que de la solution et pas de la cellule conductimétrique. C’est elle qui nous intéresse, car c’est elle qui dépend de la composition de la solution.
$µ \sigma = {Gd \over S}µ$
La conductivité s’exprime en S·m-1.
Eh bien ça ne suffirait même pas 😅, parce que si une partie des plaques est recouverte d’une couche d’oxyde, la surface « effective » n’est pas la surface réelle. Donc dans la pratique, c’est incalculable. Ce qu’on fait, c’est simplement étalonner le conductimètre de manière à prendre en compte tous ces facteurs (surface des plaques métalliques, distance entre elles, état des plaques). On plonge la cellule dans une solution étalon de conductivité parfaitement connue, et on ajuste le conductimètre pour qu’il affiche la bonne valeur de conductivité. Souvenez-vous, vous l’avez déjà fait avec le pH-mètre.
Loi de Kohlrausch
- Exploiter la loi de Kohlrausch pour déterminer une concentration ou une quantité de matière. Citer les domaines de validité de cette relation.

Bon, maintenant on aborde quelque chose de plus important qui est à retenir. La conductivité d’une solution dépend de la concentration des ions qu’elle contient (ça, je vous l’ai déjà dit plus haut) mais aussi de la nature de ces ions. Vous pouvez intuitivement vous douter qu’un ion possédant une charge « 2+ » conduira plus efficacement le courant, toutes choses égales par ailleurs, qu’un ion ne possédant qu’une seule charge « + ».
Un autre facteur qui a son importance est la taille de l’ion solvaté. Plus cet ion est gros, plus il sera freiné par les molécules d’eau qui l’entourent et donc moins il conduira efficacement le courant.
La capacité spécifique d’un ion à conduire le courant est appelée sa conductivité ionique molaire, notée $*\lambda*$, en S·m2·mol-1. Vous la trouverez dans des tables sur internet, comme celle-ci. Elle dépend (un peu) de la température et les valeurs sont généralement données à 25 °C.
Et voici donc la loi de Kohlrausch :
Elle paraît compliquée, mais c’est juste parce qu’on a simplifié son écriture. 😄
Que dit-elle ? Eh bien que pour chaque ion $*X*$ présent dans la solution, vous devez calculer sa contribution à la conductivité de la solution, en multipliant sa conductivité ionique molaire $*\lambda*$ par sa concentration $*[\mathrm{X}]*$. Puis vous devez faire la somme de chacune de ces contributions pour obtenir la conductivité totale $*\sigma*$ de la solution. C’est enfantin ! 😉
Considérons par exemple une solution de chlorure de sodium ($*\ce{Na+(aq) + Cl-(aq)}*$) de concentration $*c*$. Cela signifie que $*[\ce{Na+}]*$ = $*[\ce{Cl-}]*$ = $*c*$. Pour calculer la conductivité $*\sigma*$ de cette solution, il faut faire : $µ \sigma = \lambda_\ce{Na+}·[\ce{Na+}] + \lambda_\ce{Cl-}·[\ce{Cl-}] µ$
Attention aux unités
Quand on utilise des formules de physiques (telle que la loi de Kohlrausch) en chimie, ça donne un beau bazar question unités. Lisez bien ce qui suit :
L’unité S.I. de volume, c’est… le m3. Or, les chimistes manipulent rarement des mètres cubes de solution. Ils préfèrent donc utiliser les litres (ou les millilitres). On les comprend. Mais ce n’est pas sans poser un gros piège, que je vous poserez bien-sûr 😈, dès qu’on fait des calculs de conductivité.
Regardez les unités de $*\sigma*$ (S·m-1) et de $*\lambda*$ (S·m2·mol-1). L’unité de longueur utilisée est l’unité S.I., c’est-à-dire le mètre. Donc la concentration doit être exprimée non pas en mol·L-1, parce que le litre n’est pas l’unité S.I. de volume, mais bien en mol·m-3. Et comme il y a 1000 L dans 1 m3, 1 mol·L-1 = 1000 mol·m-3.
Accessoirement, vous pouvez aussi retenir que 1 mmol·L-1 = 1 mol·m-3. C’est bien pratique.
Mais ce n’est pas tout ! Comme si cet embrouillamini ne suffisait pas, les chimistes en rajoutent une couche. 😵 Ils ont l’habitude d’exprimer la conductivité d’une solution non pas en S·m-1, mais en S·cm-1 voire en mS·cm-1. C’est d’ailleurs dans cette unité que les conductimètres affichent la conductivité d’une solution. Retenez que 1 S·m-1 = 10 mS·cm-1. C’est facile à démontrer mais ce n’est pas l’endroit ici.
Allez, deux petits exercices pour digérer tout ça, parce que mine de rien ce que je viens de vous raconter est très dense.
Calculs de conductivité
Calculer la conductivité des solutions ci-dessous.
Conductivités molaires ioniques
- $*\ce{Na+}*$ : 5,01 mS·m2·mol-1
- $*\ce{Cl-}*$ : 7,63 mS·m2·mol-1
- $*\ce{K+}*$ : 7,35 mS·m2·mol-1
- $*\ce{SO4^2-}*$ : 16,0 mS·m2·mol-1
1. Solution de chlorure de sodium ($*\ce{Na+(aq) + Cl-(aq)}*$) à 10 mmol·L-1
2. Solution de sulfate de potassium ($*\ce{2K+(aq) + SO4^2-(aq)}*$) à 50 mmol·L-1
3. Solution mixte de sulfate de potassium et de sodium, avec $*\ce{[K+]}*$ = 20 mmol·L-1 et $*\ce{[Na+]}*$ = 10 mmol·L-1
Correction
Rappelez-vous que 1 mmol·L-1 = 1 mol·m-3.
1. $*\sigma*$ = 5,01×10 +7,63×10 = 126 mS·m-1
2. $*\sigma*$ = 7,35×2×50 + 16×50 = 1,54 S·m-1
3. $*\sigma*$ = 7,35×20 + 5,01×10 + 16×(30/2) = 0,437 S·m-1
Calculs de concentration
Calculer la concentration des solutions ci-dessous. Voir l’exo précédent pour les données.
1. Solution de chlorure de sodium de conductivité $*\sigma*$ = 0,20 S·m-1
2. Solution de sulfate de potassium de conductivité $*\sigma*$ = 353 mS·m-1
Correction
1. $*c*$ = 0,20÷(5,01·10-3+7,63·10-3) = 15,8 mol·m-3 ou mmol·L-1
2. $*c*$ = 0,353÷(2×7,35·10-3+16,0·10-3) = 11,5 mol·m-3 ou mmol·L-1
Dosage conductimétrique
Bon, nous voilà au cœur de notre sujet. Mais on en a déjà tellement dit au préalable, que ce qui reste à voir est très simple.
Le principe du dosage par étalonnage est le suivant :
- On dispose d’une solution dont on connaît la composition chimique, mais dont on ignore la concentration précise. C’est ce qu’on appelle la solution à doser ou solution « inconnue ».
- On prépare d’abord une gamme de solutions de concentrations différentes à partir d’une solution-mère de concentration parfaitement connue. Ces solutions contiennent bien entendu les mêmes ions que notre solution à doser. On fait en sorte d’être sûr que la solution à doser ait bien une concentration comprise entre les deux extrémités de notre gamme de solution (voir note ci-contre ou ci-après).
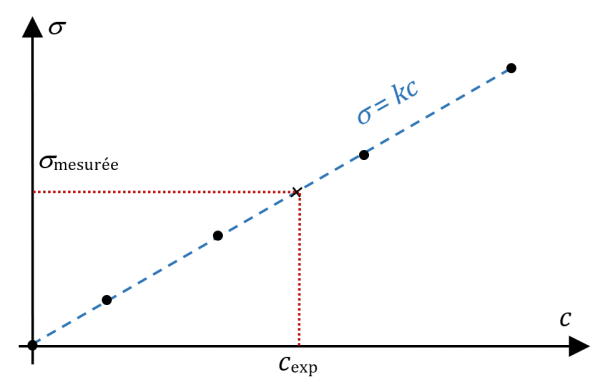
- On mesure la conductivité de ces solutions, puis on construit un graphique montrant $*\sigma = f(c)*$ pour la gamme de solutions. Ce graphique est bien entendu une droite, sauf si on travaille avec des solutions trop concentrées, ce qui est à proscrire.
- On modélise cette droite par une fonction $*\sigma = k·c*$.
- Puis on mesure la conductivité de la solution inconnue.
- Avec cette conductivité, on en déduit la concentration de la solution inconnue, en utilisant le modèle mathématique, ou par lecture graphique si on n’a qu’un graphique (ça peut arriver, en exercice).
Eh bien non ! On doit en effet avoir au moins une vague idée de sa concentration. Pour cela, il y a plein de moyens de le faire. Si par exemple on cherche à déterminer la salinité d’une eau de mer, on sait à la base qu’elle doit être comprise entre 30 et 40 g/L. Le but du dosage étant de la déterminer précisément.
Eh bien ce n’est pas un problème. D’ailleurs, cette situation arrive fréquemment. Par exemple, si on cherche à doser une eau de mer, dont la concentration en chlorure de sodium tourne autour de 0,6 mol·L-1, on ne pourra pas mesurer sa conductivité directement. Si la limite de concentration pour avoir une mesure fiable est de 10,0 mmol·L-1, il suffit alors de diluer d’un facteur 100 l’eau de mer. On aura donc une solution inconnue de concentration voisine de 6 mmol·L-1. Ensuite, une fois qu’on aura déterminé la concentration de l’eau de mer diluée, il n’y aura plus qu’à la multiplier par 100 pour obtenir la concentration de l’eau de mer de départ.
Le mieux maintenant, c’est de mettre la main à la pâte ! 😊
TP Salinité d’une eau de mer
- Mesurer une conductivité et tracer une courbe d’étalonnage pour déterminer une concentration.
Objectif : déterminer la salinité d’un échantillon d’eau de mer.
Matériel disponible
- Un échantillon d’eau de mer ;
- Une solution de chlorure de sodium de référence, notée SR, de concentration $*c_0*$ = 10,0 mmol·L-1 ;
- Un conductimètre ;
- Et toute le matériel de chimie courant dont vous aurez besoin (verrerie, eau distillée, …).
Conseils et explications
On supposera que l’eau de mer est une solution contenant uniquement des ions chlorure et des ions sodium. En réalité ce n’est pas tout à fait vrai, mais les autres ions présents (principalement sulfate $*\ce{SO4^2–}*$, magnésium $*\ce{Mg^2+}*$ et calcium $*\ce{Ca^2+}*$) sont en quantité suffisamment faible pour ne pas remettre en cause les résultats obtenus dans ce TP. La salinité d’une eau de mer est généralement comprise entre 30 et 40 g·L-1 de chlorure de sodium.
Un conductimètre ne peut pas mesurer une conductivité trop élevée. Dans le cas d’une solution de chlorure de sodium, on se limitera à une concentration de 10 mmol·L-1 pour avoir des résultats fiables.
Veillez à n’utiliser que de la vaisselle extrêmement propre et rincée à l’eau distillée. Vérifier également la qualité de votre eau distillée. Sa conductivité ne doit pas excéder ~ 0,03 mS·cm-1.
Données : $*M(\ce{Cl})*$ = 35,5 g·mol-1 ; $*M(\ce{Na})*$ = 23,0 g·mol-1.
Questions préalables
1. Donner une estimation de la concentration molaire en chlorure de sodium de l’eau de mer.
2. Quel problème va apparaître si on veut mesurer sa conductivité ?
3. Comment contourner ce problème ?
Travail demandé
Votre objectif : déterminer la concentration en chlorure de sodium de l’échantillon d’eau de mer mis à votre disposition.
- Élaborer un protocole (sans trop rentrer dans les détails) permettant, avec le matériel dont vous disposez, de déterminer la concentration de l’échantillon d’eau de mer en chlorure de sodium.
✋ Vous décrirez comme réaliser une dilution précise. - Réaliser le protocole que vous avez décrit.
- Tracer le graphique $*\sigma = f(c)*$.
- En déduire la concentration massique en chlorure de sodium de l’échantillon d’eau de mer fournie. Cette concentration est-elle cohérente avec les indications du paragraphe Conseils et explications ?
Dosage d’un sérum physiologique
Un sérum physiologique est un liquide présentant la même osmolarité que le sang. La solution est composée d’eau distillée et de chlorure de sodium ($*\ce{NaCl}*$) à 0,90 g·L-1. On se propose de vérifier la concentration d’un sérum physiologique par un dosage conductimétrique par étalonnage. Pour cela, on réalise une gamme de solutions de chlorure de sodium de concentration connue, dont on mesure la conductivité. Toutes les solutions sont prises à 25 °C.
| Solution | Concentration (mmol·L-1) | Conductivité (mS·cm-1) |
|---|---|---|
| S1 | 10,0 | 1,27 |
| S2 | 7,5 | 0,94 |
| S3 | 5,0 | 0,62 |
| S4 | 2,5 | 0,32 |
Données
- $*\lambda_\ce{Na+}*$ = 5,0 mS·m2·mol-1 $*\lambda_\ce{Cl-}*$ = 7,6 mS·m2·mol-1
- $*\lambda_\ce{HO-}*$ = 19,8 mS·m2·mol-1 $*\lambda_\ce{H3O+}*$ = 35,0 mS·m2·mol-1
- Masse molaire du chlorure de sodium : 58,8 g·mol-1.
1. Vérifier que la conductivité de la solution S1 est proche de la valeur théorique attendue. Donnée : 1 S·m-1 = 10 mS·cm-1.
2. Tracer la droite d’étalonnage. Quel point peut-on rajouter sur ce graphique ?
On dilue deux fois la solution physiologique, puis on mesure la conductivité de cette solution diluée. On trouve $*\sigma*$ = (0,97 ± 0,005) mS·cm-1.
3.a. En déduire la concentration de la solution physiologique et comparer avec le résultat attendu.
3.b. Donner un encadrement de la concentration de cette solution. On considère que l’incertitude sur le facteur de proportionnalité entre $*\sigma*$ et $*c*$ est négligeable.
4. Proposez une explication au fait que l’on ait dilué la solution physiologique avant de mesurer sa conductivité.
Correction
1. $*\sigma_{th}*$ = 5,0×10 + 7,6×10 = 126 mS·m-1 = 0,126 S·m-1 = 1,26 mS·cm-1.
2. Graphique
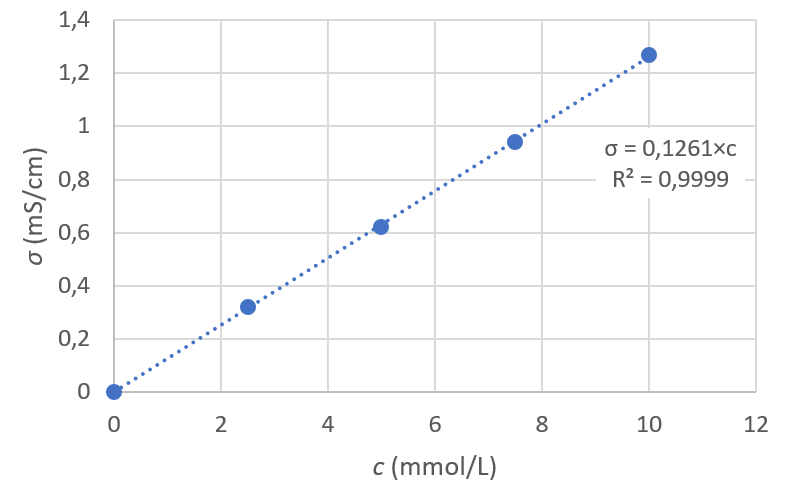
On peut rajouter le point (0 ; 0) sur la figure.
3.a $*c_{exp}*$ = 0,97÷0,1261 = 7,69 mmol·L-1.
Il ne faut pas oublier de multiplier par deux car on a dilué d’un facteur 2 la solution physiologique… 😊
Donc $*c_{sol phy}*$ = 15,4 mmol·L-1, soit 15,4·10-3×58,5 = 0,90 g·L-1.
3.b Incertitude relative sur $*\sigma*$ : $* \frac {\Delta \sigma}\sigma *$ = 0,005÷0,97 = 0,52 %.
La concentration est proportionnelle à la conductivité, donc l’incertitude relative sur $*c*$ est aussi de 0,52 %
On trouve donc une incertitude absolue de 0,005 g·L-1.
On en déduit l’encadrement de $*c*$ : 0,895 g·L-1 ≤ $*c*$ ≤ 0,905 g·L-1.
4. La solution physiologique est trop concentrée pour pouvoir exploiter la droite d’étalonnage.
Révision & entraînement
Dosage spectro de l’éthanol
D’après un exercice de bac – Amérique du Sud 2013
Définition : le titre alcoométrique d’une boisson alcoolisée, exprimé en degré, est égal au nombre de litres d’éthanol contenus dans 100 litres de cette boisson.
Données : $*M*$(éthanol) = 46,0 g·mol-1 ; $*d*$(éthanol) = 0,78
Afin de procéder au contrôle, on réalise le titrage par spectrophotométrie du vin en suivant le protocole suivant :
- 1e étape : on recueille l’éthanol du vin par distillation.
- 2e étape : l’éthanol est transformé en éthanal grâce à un oxydant noté NAD+. La réaction produit de la nicotinamide-adénine-dinucléotide réduite (NADH) en quantité de matière égale à celle de l’éthanol dosé selon l’équation :
Éthanol + NAD+ → Éthanal + NADH + H+. - 3e étape : La NADH absorbant dans le domaine UV, on mesure son absorbance par spectrophotométrie.
L’étalonnage du spectrophotomètre avec différentes solutions d’éthanol permet de vérifier la loi de Beer-Lambert : $*A = k·C_m*$ avec $*k*$ = 1,6·10-3 L·mg-1 et $*C_m*$ la concentration massique d’éthanol dans l’échantillon.
Réalisation de la mesure : on distille 10 mL de vin ; le distillat est ensuite ajusté à 100 mL avec de l’eau distillée pour obtenir une solution appelée S.
On prépare l’échantillon à doser par spectrophotométrie en introduisant dans une fiole jaugée de 100 mL :
- 1 mL de solution S,
- le catalyseur,
- NAD+ en excès,
On complète avec de l’eau distillée.
L’absorbance mesurée pour cet échantillon vaut : $*A_e*$ = 0,15.
1. Déterminer à partir de l’absorbance mesurée $*A_e*$, la concentration massique $*C_m*$ en éthanol de l’échantillon étudié.
2. En tenant compte des deux dilutions successives, calculer la concentration massique en éthanol dans le vin.
3. Quelle est la valeur du titre alcoométrique exprimé en degrés du vin ?
Correction
1. $*C_m*$ = 93,8 mg/L.
2. L’absorbance est celle de la solution S diluée 100 fois. Donc la concentration de la solution S vaut : $*C_S*$ = 9,38 g/L.
La solution S correspond elle-même à du vin dilué 10 fois. Donc la concentration du vin vaut $*C_V*$ = 93,8 g/L.
93,8 g d’éthanol ont un volume de 120 mL.
3. Le titre alcoométrique du vin est de 12°.
Dosage de l’iodure de potassium
Pour déterminer la concentration d’une solution d’iodure de potassium ($*\ce{K+(aq)}*$ ; $*\ce{I−(aq)}*$), on procède à un dosage par étalonnage en mesurant la conductivité $*\sigma*$ de plusieurs solutions d’iodure de potassium de concentration connue.
| Concentration (mmol·L-1) | Conductivité (mS·cm-1) |
|---|---|
| 1,0 | 3,43 |
| 2,0 | 6,85 |
| 3,0 | 10,3 |
| 4,0 | 13,7 |
| 5,0 | 17,2 |
| 6,0 | 20,6 |
1. Tracer la courbe $*σ=f(c)*$ à l’aide d’un tableur ou sur la calculatrice.
On plonge la même cellule de mesure dans la solution à analyser. La conductivité mesurée est $*\sigma*$ = 16,3 mS·cm-1.
2. Déterminer la concentration de la solution analysée.
Correction
Pour la question 1, débrouillez-vous 😊
2. Excel permet de trouver la valeur de $*k*$ dans $*\sigma = k·c *$.
$*k*$ = 3,433 mS·L·cm-1·mmol-1.
Donc $*c*$ = 4,75 mmol·L-1.
Nombre d’hydratation
Le phosphate de cobalt (II) se trouve sous forme d’un solide hydraté, dont la formule est $*\ce{Co3(PO4)2}, x \ce{H2O(s)}*$. Suivant la valeur de $*x*$, le phosphate de cobalt présente une couleur variant du rose au violet foncé. On cherche à déterminer $*x*$ pour le pigment violet.
Pour cela, on dissout $*m*$ = 2,52 g de phosphate de cobalt hydraté dans 1000 mL de solution, puis on mesure la conductivité $*\sigma*$ = 438 mS·m-1.
Conductivités ioniques molaires :
$*\lambda_\ce{PO_4^{3-}}*$ = 27,8 mS·m2·mol-1
$*\lambda_\ce{Co^{2+}}*$ = 11,0 mS·m2·mol-1
1. Déterminer la concentration en quantité de matière $*c*$ en soluté apporté.
2. Calculer la masse $*m'*$ de phosphate de cobalt $*\ce{Co3(PO4)2}*$ présent dans la solution.
3. En déduire la valeur de $*x*$.
Correction
1. on a $* \sigma = \lambda_\ce{Co^{2+}}×3c + \lambda_\ce{PO_4^{3-}}×2c *$ car 1 mol de $*\ce{Co3(PO4)2}*$ produit 3 mol de $*\ce{Co^{2+}}*$ et 2 mol de $*\ce{PO_4^{3-}}*$. Donc : $µ c = \frac{\sigma}{3 \lambda_\ce{Co^{2+}} + 2 \lambda_\ce{PO_4^{3-}}} µ$ $*c*$ = 4,94 mol·m-3 ou mmol·L-1.
2. Masse molaire du phosphate de cobalt (consulter un tableau périodique pour trouver les masses molaires atomiques) : 366,7 g·mol-1.
Donc $*m'*$ = 1,81 g
3. Sur les 2,52 g dissous dans la solution, il y a 1,81 g de $*\ce{Co3(PO4)2}*$. Le reste (0,71 g), c’est de l’eau.
L’eau représente 0,71/1,81 = 39 % de la masse de $*\ce{Co3(PO4)2}*$ pur. Donc une mole de $*\ce{Co3(PO4)2}*$ (366,7 g) est associée à 143 g d’eau, soit 7,94 mol d’eau. Donc $*x*$ = 8 (il y a une incertitude de mesures).
Boisson isotonique
Cet exercice a été donné en devoir en 2020/2021
Au cours d’un marathon, une coureuse perd environ 2 litres par heure de course. La marathonienne décide d’assurer ses besoins en eau à l’aide d’une boisson isotonique qui contient notamment des « sucres libres » et un colorant alimentaire, le bleu brillant.
Dans cet exercice, on s’interroge sur les risques liés aux quantités de bleu brillant et de « sucres libres » ingérées lors d’un marathon, si la marathonienne ne consomme que cette boisson.
Concernant le sucre, l’OMS recommande que l’apport énergétique dû aux « sucres libres » ne dépasse pas 10% des besoins énergétiques journaliers.
Le bleu brillant a une dose journalière admissible (DJA) de 12,5 milligrammes par kilogramme de masse corporelle.
La quantité de bleu brillant présente dans la boisson isotonique n’est pas indiquée. Pour la déterminer, on réalise l’expérience suivante :
- à partir d’une solution mère S0 de bleu brillant de concentration molaire $*C_0*$ = 0,100 mmol·L-1, on prépare par dilution six solutions aqueuses Si de volume $*V*$ = 100,0 mL en prélevant un volume $*V_i*$ de solution mère ;
- après réglage du spectrophotomètre à 630 nm, on mesure l’absorbance de chacune des solutions Si ainsi que celle de la boisson.
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| $*V_i*$ (mL) | 1,0 | 2,0 | 3,0 | 5,0 | 8,0 | 10,0 |
| Absorbance | 0,134 | 0,259 | 0,434 | 0,745 | 1,150 | 1,402 |
L’absorbance de la boisson isotonique est égale à 0,789.
Données
- masse molaire du bleu brillant : 793 g·mol-1 ;
- énergie apportée par les « sucres libres » contenus dans 100 mL de boisson isotonique : 68,5 kJ ;
- besoins énergétiques pour la marathonnienne, le jour d’un marathon : 19·103 kJ
- la masse corporelle de la marathonienne est de 50 kg.
Questions préliminaires
1. Déterminer le volume maximal de boisson isotonique que la marathonienne peut ingérer le jour du marathon pour suivre les recommandations de l’OMS concernant les « sucres libres ».
2. Calculer la valeur de la concentration molaire en bleu brillant de la solution S5 obtenue par dilution.
Problème
Lors d’un marathon de 4 h, si la marathonienne décide de compenser la totalité de l’eau perdue en buvant uniquement la boisson isotonique étudiée, cela pose-t-il un problème pour sa santé ?
Correction
1. Besoin journalier pour la marathonienne : 19 MJ. Donc l’apport énergétique par glucides libres ne doit pas excéder 1,9 MJ. Elle peut donc boire 1900÷68,5 = 27,7 fois 100 mL, soit 2,77 L.
2. La concentration de S5 est égale à 8 % de celle de la solution-mère, soit 0,008 mmol·L-1.
Problème
Pour une meilleur précision, on calcule la valeur moyenne du coefficient d’absorption de la loi de Beer-Lambert. On trouve 0,140 L·µmol-1.
Remarque : ce n’est pas la meilleure manière de faire, mais vous n’avez pas accès à un tableur pour vous trouver la droite de régression.
Donc la concentration de la boisson isotonique en bleu brillant est de 0,789÷0,140 = 5,6 µmol·L-1.
Calcul de sa concentration massique : 5,6·10-6×793 = 4,5 mg·L-1.
En 4 h de marathon, la coureuse boit 2×4 = 8 L.
• Pour les sucres libres, c’est trop (limite = 2,77 L).
• Pour le bleu brillant, cela représente 4,5×8 = 36 mg. Or, la DJA, pour un poids de 50 kg, vaut 50×12,5 = 625 mg. On est donc très loin de la limite.