P3. Orbites
Les lois de Newton permettent également de prévoir le mouvement d’un corps en orbite autour d’un autre. Mais cette situation est plus complexe, dans sa forme générale, que ce qu’on a vu au chapitre précédent (mouvement dans un champ uniforme), car justement, le champ (ici, le champ gravitationnel), n’est pas uniforme.
En effet, dans le plus simple des cas, c’est-à-dire une orbite circulaire, l’intensité du champ reste constant (car la distance $*d*$ entre le centre de gravité de l’astre attracteur et le centre de gravité de l’orbiteur reste constante), mais sa direction change au cours du mouvement de l’orbiteur.
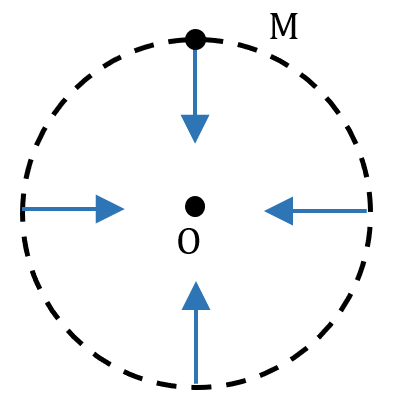
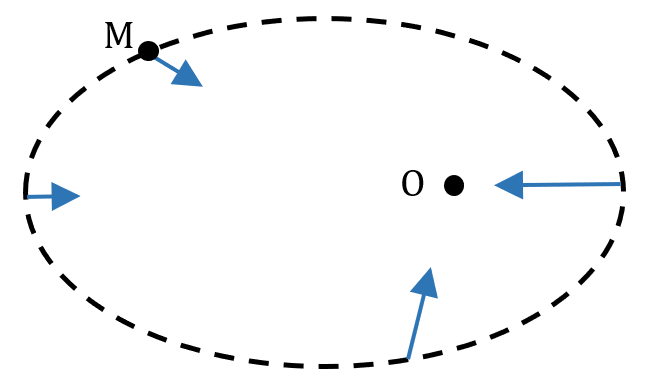
Et dans le cas général, l’orbite n’est pas circulaire, mais elliptique et donc cette distance $*d*$ change également au cours du mouvement, entraînant une variation de l’intensité du champ de pesanteur.
Dans tous les cas, le centre de masse de l’astre attracteur se trouve dans le plan de l’orbite.
Repère de Frenet
- Citer et exploiter les expressions des coordonnées des vecteurs vitesse et accélération dans le repère de Frenet, dans le cas d’un mouvement circulaire.
Étudier un mouvement circulaire dans un repère classique (deux axes fixes portant deux vecteurs unitaires fixes), c’est possible, mais c’est compliqué. On peut choisir un repère qui va nous simplifier certains calculs. C’est le repère de Frenet.
Base vectorielle
Vous avez très certainement déjà vu ça en math. Les vecteurs unitaires définissent un repère. On dit qu’ils forment une base vectorielle. Par exemple, dans un repère cartésien à 3 dimensions (celui que vous connaissez, avec les trois coordonnées $*x*$, $*y*$ et $*z*$), il y a trois vecteurs unitaires. Celui définissant l’axe $*\mathrm{O}x*$, qu’on note souvent $*\vec{i}*$ en math ou $*\vec{u}_x*$ en physique. Sa direction et son sens sont celui de l’axe $*\mathrm{O}x*$, et sa norme vaut 1 (d’où le nom « unitaire »). Pareil pour les axes $*\mathrm{O}y*$ et $*\mathrm{O}z*$.
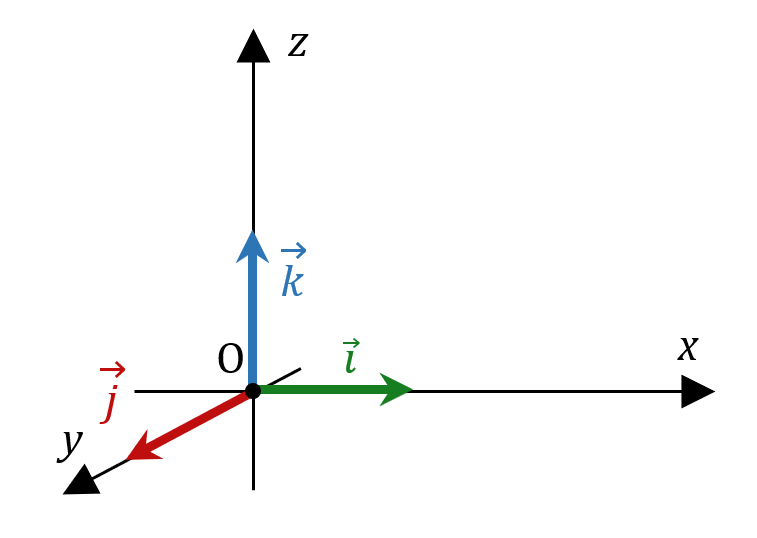
Donc en fait, écrire les coordonnées d’un vecteur sous la forme : $µ \vec{v} \begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} µ$ c’est équivalent à écrire : $*\vec{v} = v_x\vec{i} + v_y\vec{j} + v_z\vec{k} *$
Décrire un mouvement circulaire
Mais revenons à nos 🐑. Imaginons que l’on veuille décrire le mouvement circulaire uniforme d’un point M autour de l’origine du repère.
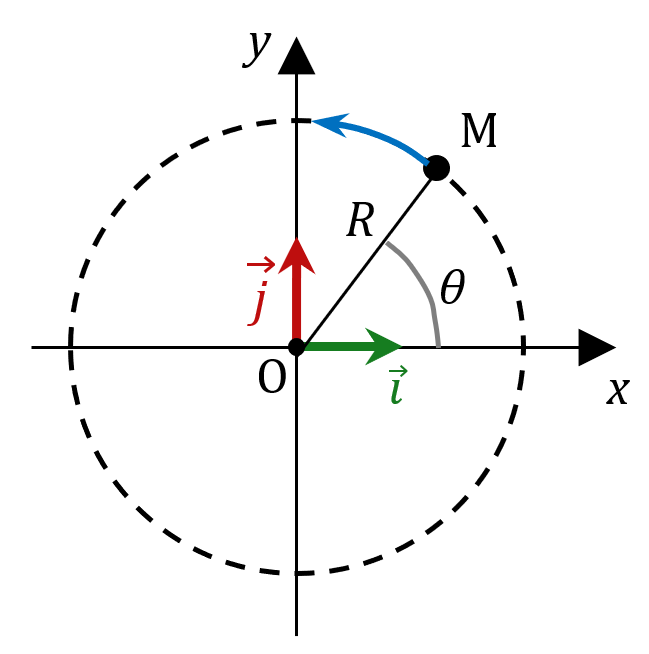
Les coordonnées du vecteur $*\overrightarrow{\mathrm{OM}} *$ sont : $*x(t)=R\cos(\theta)*$ et $*y(t)=R\sin(\theta)*$, avec $*\theta = \omega t*$, $*\omega*$ (lettre grecque oméga minuscule) étant une constante proportionnelle à la vitesse de rotation de M.
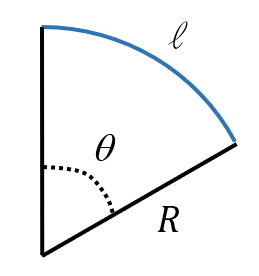 La longueur de l’arc de cercle $*\ell*$ est donnée par $*\ell = R\,\theta*$,
où $*R*$ est le rayon du cercle et $*\theta*$ l’angle qui définit les
extremités de l’arc de cercle, exprimé en radians.
La longueur de l’arc de cercle $*\ell*$ est donnée par $*\ell = R\,\theta*$,
où $*R*$ est le rayon du cercle et $*\theta*$ l’angle qui définit les
extremités de l’arc de cercle, exprimé en radians.Si vous ne connaissiez pas cette relation, je vous conseille de la graver dans votre mémoire. Elle est très utile. 🤓
Je ne vais pas ici vous faire le calcul des coordonnées du vecteur vitesse et accélération, même si vous seriez capable de le faire, car vous savez dériver les fonctions sinus et cosinus, non ? 😉
Mais vous pouvez bien vous douter que ça ne va pas être quelque chose de super simple…
Et c’est là que, en bon physicien, on va aller au plus simple en choisissant une autre base de vecteurs, qui vont considérablement nous simplifier la vie. Cette base va définir le repère de Frenet.
Définition du repère de Frenet
Le repère de Frenet sert essentiellement à décrire des mouvements circulaires (ou des portions de mouvement que l’on peut assimiler, momentanément, à un cercle). Comme le mouvement est à deux dimensions (on va revenir dessus plus loin dans ce chapitre), on n’a besoin que de deux vecteurs unitaires.
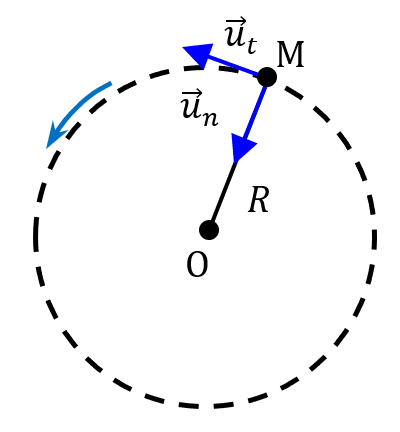
L’origine du repère est le point mobile lui-même. Donc, dans ce repère, on ne peut pas exprimer la position du mobile, mais on s’en fiche, ce n’est pas son but.
Si, on peut quand-même obtenir des choses intéressantes. Le repère de Frenet ne va pas nous permettre de tout calculer pour un mouvement circulaire. En fait, il ne sert qu’à exprimer simplement la vitesse et l’accélération du point mobile. Si on veut vraiment pouvoir calculer la position du point M à chaque instant, il faut faire des maths un peu plus complexes que ça, que vous seriez d’ailleurs parfaitement en mesure de comprendre, mais c’est pas au programme. Et il y a déjà assez de trucs à voir comme ça … 😅
Mais reprenons ! Les deux vecteurs de la base associée au repère de Frenet sont $*\vec{u}_t*$ (pour vecteur unitaire tangentiel) et $*\vec{u}_n*$ (pour vecteur unitaire normal c’est-à-dire perpendiculaire à $*\vec{u}_t*$).
Vecteur $*\vec{u}_t*$
$*\vec{u}_t*$ est tangent à la trajectoire (le plus souvent un cercle, mais ce n’est pas une obligation) et son sens est celui du déplacement du mobile. Du coup, l’expression du vecteur vitesse est super simple dans cette base. C’est :
$µ \vec{v} = v·\vec{u}_t µ$
N’oubliez pas, $*\vec{u}_t*$ est un vecteur unitaire. Ça veut dire que sa norme vaut 1. Dans la relation vectorielle ci-dessus, le vecteur $*\vec{u}_t*$ indique la direction est le sens du vecteur $*\vec{v}*$ qui, je vous le rappelle, est forcément tangent à la trajectoire.
Vecteur $*\vec{u}_n*$
$*\vec{u}_n*$ est perpendiculaire à $*\vec{u}_t*$ et pointe vers l’intérieur de la trajectoire. Du coup, si la trajectoire est un cercle, $*\vec{u}_n*$ point vers le centre du cercle, mais attention ! Ce n’est vrai que si la trajectoire est un cercle.
Eh bien si la trajectoire est rectiligne, utiliser le repère de Frenet n’est pas très pertinent. Et si vous insistez pour l’utiliser quand-même, alors c’est vous qui choisissez vers où il pointe…
On en a besoin pour exprimer le vecteur accélération. J’y viens.
Vecteur accélération dans le repère de Frenet
Bon, que sait-on de l’accélération ? Eh bien on sait que, par définition, $µ \vec{a} = {\mathrm{d}\vec{v} \over \mathrm{d}t } µ$
D’autre part, on vient de voir que, dans le repère de Frenet, $* \vec{v} = v·\vec{u}_t *$. Du coup, si on associe ces deux relations, on obtient que : $µ \vec{a} = {\mathrm{d}(v\,\vec{u}_t) \over \mathrm{d}t } µ$
Et c’est là que les choses se compliquent (un peu). En effet, $*\vec{u}_t*$ n’est pas constant.
Sa norme, oui ! Mais à mesure que le mobile se déplace sur sa trajectoire, sa direction change. Eh oui ! Il reste toujours tangent au cercle, donc pour ça, sa direction doit changer. Et donc le vecteur $*\vec{u}_t*$ n’est pas constant, même si ça norme l’est. Du coup, nous devons dériver le produit $*v\,\vec{u}_t*$ par rapport au temps
Vous savez dériver un produit de fonction. Rappelez-vous : $*(uv)' = u'v + uv'*$, comme on l’écrit en mathématique. Alors pour notre vecteur accélération, ça devient : $µ \vec{a} = {\mathrm{d}(v\,\vec{u}_t) \over \mathrm{d}t } = {\mathrm{d}v \over \mathrm{d}t }\vec{u}_t + v {\mathrm{d}\vec{u}_t \over \mathrm{d}t } µ$
Je vous demande d’accepter le fait que : $µ{\mathrm{d}\vec{u}_t \over \mathrm{d}t } = \frac vR \vec{u}_n µ$ $*R*$ étant le rayon de la trajectoire circulaire.
On arrive enfin au point d’orgue de ce paragraphe : le vecteur accélération dans le repère de Frenet s’écrit :
Attention ! remarquez bien que $*{\mathrm{d}v \over \mathrm{d}t }*$ représente la dérivée de la valeur de la vitesse par rapport au temps, et non la dérivée du vecteur vitesse. Du coup, dans le cas d’un mouvement circulaire uniforme, $*{\mathrm{d}v \over \mathrm{d}t } = 0*$
Ça fait beaucoup d’information d’un coup, mais si vous avez noté l’essentiel sur votre synthèse, vous devriez constater qu’il n’y a pas énormément de chose à retenir : il faut connaître la définition du repère de Frenet, l’expression de $*\vec{v}*$ et l’expression de $*\vec{a}*$. On va maintenant faire un petit exercice d’application.
Gravité artificelle dans l’espace
Vous avez certainement vu des films de science-fiction où un vaisseau spatial comporte un anneau d’habitations qui tourne autour de son axe central

Le principe de cette structure est de recréer une sorte de gravité artificielle pour ses occupants, en faisant tourner le vaisseau sur lui-même. Les occupants de l’anneau sont soumis à une « force centrifuge » qui remplace le poids.
L’utilisation du repère de Frenet va nous permettre de faire quelques petits calculs simples à propos de cette situation.
Données
- Diamètre de la structure : 300 m ;
- Vitesse de rotation : constante, 1 tour par minute.
1. Quelle est la vitesse d’un point fixe de la roue par rapport au centre de son mouvement ?
2. Donner l’expression vectorielle de la vitesse dans le repère de Frenet.
3. Donner l’expression vectorielle de l’accélération dans le repère de Frenet. Quel est sa direction ? Son sens ?
4. Une accélération de 9,81 m·s-2 donnera l’impression d’avoir le même poids sur Terre. Est-ce le cas ici ?
5. Déterminer quelle devrait être la vitesse de rotation $*\omega*$, en tours par minute, de la structure pour que leurs occupants aient l’impression d’être dans un champ gravitationnel identique à celui de la surface terrestre (noté $*g*$). Je veux du calcul littéral.
Correction
1. Le point fixe sur la roue (dans l’anneau extérieur) parcourt le diamètre du cercle ($*2\pi R*$ = 942 m) en une minute. Sa vitesse est donc de 942÷60 = 15,7 m·s-1.
2. $*\vec{v} = v·\vec{u}_t*$ que l’on peut encore écrire : $*\vec{v} = 15,7\vec{u}_t*$
3. Le mouvement est circulaire uniforme, donc la valeur de la vitesse ne varie pas. Il s’en suit que : $µ\vec{a} = \frac {v^2}R·\vec{u}_n µ$ Ce vecteur est colinéaire au rayon du cercke et il pointe vers son centre.
4. La valeur de l’accélération est : $*v^2/R =*$ 1,6 m·s-2. On est très loin de la valeur de l’accélération de l’attraction gravitationnelle à la surface de la Terre.
On veut que : $µ\begin{aligned} \frac {v^2}R &= g \\ v &= \sqrt{gR} \\ \frac {2\pi R \omega}{60} &= \sqrt{gR} \\ \omega &= \frac {60\sqrt{gR}} {2\pi R} \\ \omega &= \frac {60\sqrt{g}}{2\pi\sqrt{R}} \\ \end{aligned} µ$
Après une application numérique qu’il est inutile de détailler, on trouve $*\omega*$ = 2,44 tr·min-1
Orbite circulaire
- Déterminer les caractéristiques des vecteurs vitesse et accélération du centre de masse d’un système en mouvement circulaire dans un champ de gravitation newtonien.
Un satellite peut avoir un mouvement circulaire autour de son astre attracteur. C’est une situation très particulière dont on reparlera lorsqu’on traitera, dans le paragraphe suivant, le cas général d’une orbite elliptique. C’est la plus simple mathématiquement.
Pour étudier les caractéristiques d’une orbite circulaire, on se place dans le repère de Frenet.
$*\vec{u}_n*$ est perpendiculaire à $*\vec{u}_t*$ et pointe vers l’intérieur de la trajectoire
Le repère suit le mobile au cours de son déplacement.
Vecteur accélération
On obtient le vecteur accélération grâce à la RFD. L’orbiteur (S) de masse $*m*$ est attiré par l’astre attracteur (O) de masse $*M*$ avec une force $*\vec{F}*$ telle que : $µ \vec{F} = \frac {GMm}{d^2}\vec{u}_n µ$
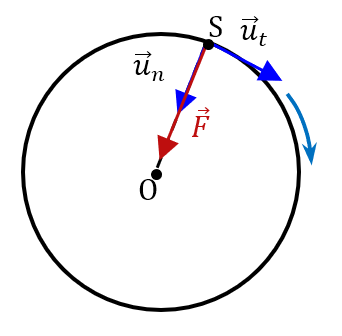
Cette relation, que vous avez déjà vue plein de fois, mérite ici quelques petits rappels :
- $*d*$ est la distance entre le centre de gravité de O et le centre de gravité de S. Elle est également parfois notée $*r*$.
- $*\vec{F}*$ et $* \vec{u}_n*$ sont colinéaire uniquement dans le cas d’un mouvement circulaire. Relisez la définition du repère de Frenet si ce n’est pas clair pour vous !
- Toutes les grandeurs doivent bien-sûr être exprimées en unité S.I.
Puisque la seule force exercée sur l’orbiteur est la force d’attraction gravitationnelle exercée par l’astre attracteur, la RFD devient ici : $µ m\vec{a} = \frac {GMm}{d^2}\vec{u}_n µ$ D’où :
Voilà donc comment on obtient le vecteur accélération de l’orbiteur. Jusque là, il n’y a rien de nouveau.
Vecteur vitesse
Là, ça devient un peu plus compliqué. Comment fait-on pour en déduire le vecteur vitesse à partir du vecteur accélération ?
Oui, c’est tout à fait vrai. Mais… en utilisant le repère de Frenet, on rend cette méthode très compliquée, car les vecteurs unitaires $*\vec{u}_t*$ et $*\vec{u}_n*$ changent de direction tout au long du mouvement. Ils ne sont pas constants, donc il faudrait en tenir compte lors de cette intégration, ce qui compliquerait beaucoup les calculs.
Eh bien rappelez-vous de l’expression du vecteur accélération dans un repère de Frenet : $µ \vec{a} = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{u}_t + \frac{v^2}d\vec{u}_n \tag{2} µ$
Cette relation va nous permettre de déduire la vitesse de l’orbiteur assez simplement. On peut déjà écrire, d’après les équation (1) et (2) : $µ \frac{\mathrm{d}v}{\mathrm{d}t}\vec{u}_t + \frac{v^2}d\vec{u}_n = \frac {GM}{d^2}\vec{u}_n µ$
Ensuite, comme il s’agit d’une relation vectorielle, on peut écrire cette égalité selon chacun des vecteurs unitaires.
Selon le vecteur $*\vec{u}_t*$, on obtient : $µ \frac{\mathrm{d}v}{\mathrm{d}t} = 0 \tag{3} µ$
Cette égalité montre que la valeur de la vitesse est constante.
Et selon le vecteur $*\vec{u}_n*$, on obtient : $µ \frac{v^2}d = \frac {GM}{d^2} \tag{4} µ$
D’où il ressort deux choses très intéressantes : d’abord, d’après (3), on voit que la valeur de la vitesse est constante.
Ensuite, on peut calculer cette valeur d’après (4).
$µ v = \sqrt{\frac{GM}d} µ$
On a donc parfaitement déterminé le vecteur vitesse :
✋ Vous devez être capables de retrouver ces résultats. Les savoir par cœur vous servira juste à être sûr de ne pas vous être trompé.
À vous de jouer
Établir les caractéristiques des vecteurs accélération et vitesse d’un satellite en orbite circulaire autour de son astre attracteur.
Il va sans dire que vous devez essayer de le faire sans regarder le cours et en comprenant parfaitement chaque étape. 😏
Masse de la Terre
Par divers procédés astucieux élaborés par le génie de quelques savants grecs de l’Antiquité – et dont je n’ai pas le temps de discuter ici – ceux-ci savaient assez précisément :
- la valeur du diamètre de la Terre (12.800 km) ;
- que la Lune est à peu près trois fois plus petite que la Terre (3.500 km de diamètre) ;
- qu’elle se trouve à environ 400.000 km de la Terre ;
- qu’elle fait le tour de la Terre en environ 28 jours (bon, ça, les hommes préhistoriques le savaient déjà 😁)
Grâce à ces connaissances, déterminer la masse de la Terre.
Correction
On utilise $* v = \sqrt{\frac{GM}d} *$ pour déterminer $*M*$. Il faut donc calculer $*v*$ avec les données.La Lune parcourt 2$*\pi*$×400000 km en 28 jours. Ça fait une vitesse de 1,0·103 m·s-1.
On trouve donc $*M = \frac{v^2·d}G = *$ 6,5·1024 kg (valeur réelle : 6,0·1024 kg)
Il ne manquait aux Grecs que la loi de Newton pour calculer la masse de la Terre. 😊
Période orbitale
La station ISS orbite à 400 km d’altitude. En combien de temps fait-elle le tour de la Terre ?
Données : masse de la Terre $*M_T*$ = 6,0·1024 kg ; rayon de la Terre $*R_T*$ = 6,4·103 km.
Correction
Il faut d’abord calculer la vitesse de l’ISS sur son orbite, puis, connaissance la circonférence de son orbite, calculer le temps qu’elle met à parcourir cette distance.Ici, $*d*$ = 6400 + 400 = 6800 km soit 6,8·106m.
Donc $*v*$ = 7,67·103 m·s-1.
Circonférence de l’orbite : 2×$*\pi*$×6,8·106 = 4,27·107 m.
Donc $*T \simeq *$ 5,57·103 s soit environ 1h33.
Satellite géostationnaire
Un satellite est dit « géostationnaire » s’il est immobile dans le référentiel terrestre.
1. Donner les caractéristiques du mouvement orbital d’un satellite pour qu’il puisse être géostationnaire :
- Quelle doit-être la période de révolution du satellite ?
- Quelle doit être la forme de son orbite ?
- Dans quel plan doit se trouver son orbite ?
- Dans quel sens doit-il tourner autour de la Terre ?
2. Quel doit être l’altitude d’un satellite géostationnaire ?
3. À quoi un tel satellite peut-il servir ?
Correction
1. Caractéristiques de l’orbite géostationnaire :
- Période de révolution : 24h. Le satellite doit tourner à la même vitesse que la Terre sur elle-même pour pouvoir rester au-dessus du même point.
- Forme de l’orbite : circulaire. Si l’orbite est elliptique, la vitesse du satellite n’est pas constante et il ne peut donc pas rester autour du même point.
- Plan de l’orbite : plan équatoriel. Si l’orbite du satellite est inclinée par rapport au plan équatorial, celui-ci sera parfois dans l’hémisphère nord et parfois dans l’hémisphère sud. Il ne sera donc pas toujours au-dessus du même point.
- Sens de révolution : le même que celui de la Terre sur elle-même. S’il tourne dans l’autre sens, il ne pourra jamais rester au-dessus du même point.
2. On a d’une part la relation $*v = \sqrt{\cfrac{GM}{R_T+z}}*$ et d’autre part la relation $*v = \cfrac{2\pi (R_T+z)}T*$. Pour que le satellite soit géostationnaire, il faut qu’il reste toujours au-dessus du même point au sol et donc qu’il accomplisse son orbite en $*T*$ = 24 h. Donc : $µ \sqrt{\frac{GM}{R_T+z}} = \frac{2\pi (R_T+z)}T µ$ Dans cette équation, on connaît tout sauf $*z*$. On l’isole et on trouve que : $µ R_T + z = \sqrt[3]{\frac{GMT^2}{4 \pi^2}} µ$ Et donc $*z \simeq*$ 35900 km.
3. À observer toujours la même partie du globe terrestre (satellite météo) ou bien à diffuser des informations sur toujours la même zone (télévision par satellite par exemple).
Orbite elliptique
- Établir et exploiter la troisième loi de Kepler dans le cas du mouvement circulaire.
L’ellipse
C’est un rond écrasé ! 😁
Mathématiquement, pour construire une ellipse, il vous faut deux points distincts, disons A et B. L’ensemble des points M tels que $* \mathrm{AM} + \mathrm{MB} = \mathrm{constante} *$ sont situés… sur une ellipse.
A et B sont appelés les foyers de l’ellipse.
Plus l’ellipse est applatie, plus on dit que son excentricité est grande. Si les deux foyers sont confondus, alors l’excentricité de l’ellipse est nulle. Il s’agit d’un… cercle 😊
L’ellipse est la forme générale du mouvement d’un satellite autour de son astre attracteur. À moins de conditions initiales très particulières, la trajectoire d’un satellite n’est pas circulaire, mais elliptique.
C’est le cas de la trajectoire des planètes autour du Soleil, ou encore de la Lune autour de la Terre, bien que l’excentricité de ces ellipses soit faibles de sorte qu’elles puissent être assimilées à des cercles sans faire de grosses erreurs.
Lois de Kepler
Traiter mathématiquement des orbites elliptiques nécessite une certaine puissance de calcul. On ne va pas le faire ici (bien qu’avec Python on pourrait faire pas mal de choses…
Kepler a énoncé trois lois empiriques (c’est-à-dire issue de l’observation) concernant les mouvements d’astres en orbite autour d’autres astres. Ces lois ont été formulées entre 1609 et 1618, avant même que Newton ne découvre les lois de la mécanique qui portent son nom.
Elles se démontrent néanmoins mathématiquement et sont des conséquences des trois lois de Newton (qui n’ont été découvertes qu’après sa mort).
Si un corps C orbite atour d’un corps O beaucoup plus massif que lui (schéma ci-dessous), alors :
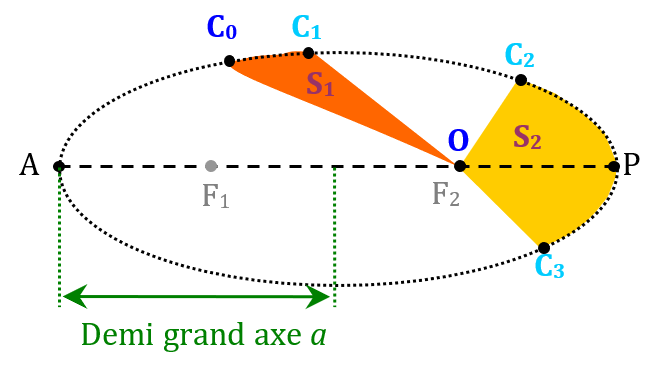

Le point le plus proche (P), est appelé le péri-astre (périgée, périhélie).
Première loi – loi des orbites
La trajectoire de C décrite une ellipse. O occupe un des foyers de cette ellipse.Deuxième loi – loi des aires
Pendant des intervalles de temps égaux, les aires balayées par OC sont égales.(Si le corps C a mis le même temps pour passer de la position C0 à C1 et de C2 à C3, alors les surfaces S1 et S2 sont égales).

Troisième loi – loi des périodes
| $µ \frac{T^2}{a^3} = \frac{4\pi^2}{GM} µ$ | $*T*$ : période de révolution du satellite (s) $*a*$ : demi grand axe (m) $*G*$ : constante de gravitation universelle $*M*$ : masse de l’astre attracteur (kg) |
Comète de Halley
La comète de Halley, en orbite autour du Soleil, a une période d’environ 76 ans.
1. Quelle est la taille, en unité astronomique, du grand axe de son orbite ?
2. Au périhélie, sa distance au Soleil est de 0,6 ua. À quelle distance du Soleil cette comète s’éloigne-t-elle au maximum ? Comparer cette distance avec la distance moyenne entre le Soleil et Pluton (40 ua).
Correction
1. En utilisant la 3e loi de Kepler, on a :
$µ a^3 = \frac{GMT^2}{4\pi^2} µ$
On trouve $*a*$ = 17,9 ua, soit un grand axe de 35,8 ua.
2. Au plus loin du Soleil, la comète se trouve à 35,2 ua du Soleil, soit une distance comparable à celle de Pluton.
3e loi de Kepler et mouvement circulaire
Dans le cas d’un mouvement circulaire, il est assez facile de démontrer la 3e loi de Kepler.
Reprenons ce qu’on avait établi au paragraphe précédent, à savoir : $µ v = \sqrt{\frac{GM}d} µ$
La période $*T*$ de l’orbite est facile à calculer : il s’agit simplement de la distance parcourue par le satellite pendant une orbite complète (donc $*2\pi d*$) divisé par la vitesse (qui est constante, je vous le rappelle) à laquelle évolue le satellite sur son orbite. Soit : $µ T = \frac{2 \pi d}{\sqrt{\frac{GM}d}} µ$
Si on élève cette relation au carré, on obtient : $µ T^2 = \frac{4 \pi^2 d^3}{GM} µ$
$*d*$ est la distance entre le centre de gravité de l’astre attracteur et le centre de gravité du satellite. C’est donc le rayon de la trajectoire.
D’autre part, le demi grand axe d’une ellipse, s’il s’agit d’un cercle, c’est… son rayon, tout simplement. Autrement dit, dans le cas d’une orbite circulaire, on a : $*a*$ = $*d*$. Et donc :
$µ \frac{T^2}{a^3} = \frac{4\pi^2}{GM} µ$
Et voilà ! On vient de démontrer la 3e loi de Kepler dans le cas d’une orbite circulaire… 😎
Le démontrer dans le cas d’une orbite elliptique, c’est une autre paire de manche… mais ce n’est pas au programme.
TP Mouvement elliptique
- Capacité numérique : exploiter, à l’aide d’un langage de programmation, des données astronomiques ou satellitaires pour tester les deuxième et troisième lois de Kepler.
Objectif : je vous propose dans ce TP de faire une simulation numérique d’un mouvement orbital, circulaire ou elliptique, puis de vérifier que les 2e et 3e lois de Kepler sont bien vérifiées dans cette simulation.
Pour ça, au lieu de faire des calculs très compliqués, on va faire beaucoup (mais alors beaucoup !) de calculs simples. Grâce à Python.
Considérations préalables
Mais avant de se lancer dans les calculs, il y a quelques points à bien clarifier.
Vecteur accélération d’un satellite
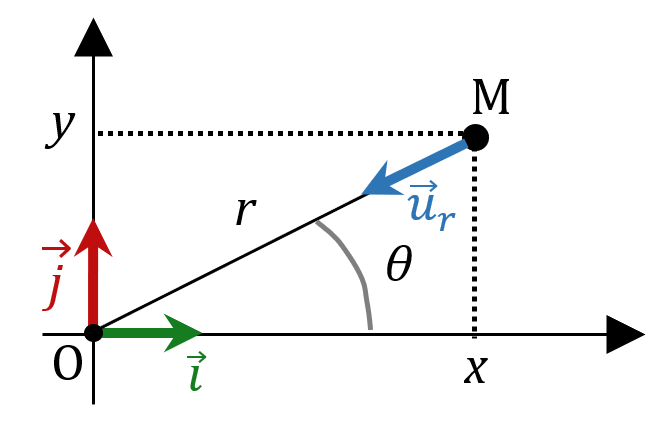
Imaginons un satellite M de masse $*m*$ se trouvant à la position de coordonnées $*x*$ et $*y*$ dans un repère cartésien, à une distance $*r*$ de l’origine où se trouve un astre attracteur très massif (et donc immobile).
Le vecteur $*\vec{u}_r*$ représenté sur le schéma est un vecteur unitaire qui par du satellite et qui pointe vers l’astre attracteur. Donc attention, $*\vec{u}_r*$ n’est pas le vecteur $*\vec{u}_n*$ du repère de Frenet, sauf si la trajectoire est circulaire. Mais dans ce TP, on ne suppose pas nécessairement que la trajectoire est circulaire ! 😊
Son vecteur accélération $*\vec{a}*$ a pour coordonnées :
$µ \vec{a} \begin{pmatrix} a_{x} = - \dfrac {GM}{r^3}x \\ a_{y} = - \dfrac {GM}{r^3}y \end{pmatrix} µ$
Démonstration
Le vecteur position $* \overrightarrow{\mathrm{OM}} *$ peut s’écrire $*-r\vec{u}_r*$ d’une part, mais il peut aussi s’écrire $*x\vec{i} + y\vec{j}*$, donc $µ -r\vec{u}_r = x\vec{i} + y\vec{j} µ$ donc $µ \vec{u}_r = -\frac xr \vec{i} - \frac yr \vec{j} µ$
Or l’expression du vecteur accélération est $µ \vec{a} = \dfrac {GM}{r^2} \vec{u}_r µ$
Donc on peut le réécrire comme ceci : $µ \vec{a} = \dfrac {GM}{r^2} (-\frac xr \vec{i} - \frac yr \vec{j}) µ$
Ce qui, après simplification, donne : $µ \vec{a} = -\dfrac {GM}{r^3} x\vec{i} - -\dfrac {GM}{r^3} y\vec{j} µ$
Méthode d’Euler
L’autre concept à bien comprendre est le suivant. Le problème qu’on a ici, c’est que le vecteur accélération dépend de la position du satellite. Et la position du satellite dépend (entre autre) de son accélération, c’est en quelque sorte le 🐈 qui se mord la queue.
Si on veut résoudre formellement le problème, on tombe sur des équations dont l’inconnue est une fonction et ses dérivées (ici la position, la vitesse et l’accélération). Ça s’appelle une équation différentielle, c’est omniprésent en physique et c’est souvent très complexe à résoudre. 😖
Mais on peut contourner le problème si on segmente les calculs en considérant que, pendant un « bref instant », l’accélération est constante. De là on peut facilement calculer l’évolution de la vitesse, puis de la position.
Avec cette nouvelle position, on peut recalculer le nouveau vecteur accélération, et ainsi de suite. En prenant des intervalles de temps très brefs, répétés des milliers de fois (voire bien plus, les super-calculateurs servent à ça), on peut également arriver à prévoir le mouvement d’un satellite, même dans le cas d’une orbite elliptique.
C’est ce qu’on appelle la méthode d’Euler. Elle est très souvent utilisée dans les simulations numériques quand les calculs sont impossibles à résoudre formellement (en météorologie, par exemple, ou pour l’écoulement trubulent de fluide, ou pour modéliser la formation du système solaire… 😊).
Exemple
Prenons un exemple simple pour fixer les idées à la fois sur le problème mathématique posé et sur la manière de le résoudre approximativement par la méthode d’Euler.
Imaginons un avion sur sa piste d’envol. Initialement immobile, ses réacteurs appliquent sur lui une force de poussée $*\vec{F}*$ constante selon l’axe $*\mathrm{O}x*$ vers les $*x*$ croissant. Le poids de l’avion compense la réaction de la piste, on peut donc ignorer ces deux forces car elles s’annulent mutuellement.
On a déjà traité ce cas en négligeant les frottements. C’est facile : l’accélération est constante ($*a_x = \frac Fm = a*$, $*m*$ étant la masse de l’avion), donc la vitesse est une fonction linéaire du temps $*v_x = at*$ (l’avion est initialement immobile) et donc sa position $*x*$ est un trinôme du temps : $*x = \frac 12 at^2*$ si la position initiale de l’avion coïncide avec l’origine du repère.
Mais si on ne néglige pas les frottements, ça devient plus compliqué. En effet, les forces de frottements, notées $*\vec{f}*$ sont proportionnelles à la vitesse et opposées au sens de déplacement de l’avion. Elles peuvent s’écrire : $*\vec{f} = -k\vec{v}*$
L’accélération s’écrit maintenant : $*a = \frac Fm - kv*$. Mais pour calculer $*v*$, il faut connaître $*a*$. Et $*a*$ dépend de $*v*$… 😓
On a donc une équation différentielle : $µ \frac {\mathrm{d}v}{\mathrm{d}t} = \frac Fm - kv µ$
Résoudre cette équation différentielle permet de trouver la fonction $*v(t)*$.
Vous apprendrez à résoudre des équations différentielles simples comme celle que je viens de vous présenter plus tard dans l’année (en math et en physique). Pour l’instant, ce n’est pas ce qui nous intéresse.
La méthode d’Euler permet de contourner cette difficulté au prix de nombreux calculs simples. Voici son principe appliqué à la situation qui nous intéresse :
- On va d’abord considéré que, pendant le premier intervalle de temps $*\Delta t*$, la vitesse est suffisamment faible pour les frottements soient négligeables (on fait donc une approximation).
On a donc une accélération qui est constante et qui vaut $*a_0 = \frac Fm*$.
Cela nous permet de calculer la vitesse après ce premier intervalle de temps : $*v_1 = a_0·\Delta t*$. - Puis on prend un deuxième intervalle $*\Delta t*$, pendant lequel on considère que les forces de frottement sont constantes et valent $*f_1 = k·v_1*$.
L’accélération sera donc constante et vaudra $*a_1 = \frac Fm - k·v_1*$.
La vitesse $*v_2*$ après ce deuxième intervalle de temps sera : $*v_2 = v_1 + a_1·\Delta t*$. - Et on continue comme ça pour chaque intervalle de temps.
Il est important que vous remarquiez qu’on fait des approximations (on considère que la valeur des forces de frottement est constante pendant chaque intervalle de temps). L’approximation est d’autant meilleure que l’intervalle de temps est court. Mais plus vous prenez un intervalle de temps court, plus vous devrez faire de calculs pour étudier le mouvement pendant une durée donnée.
Il s’agit donc de choisir comme valeur de $*\Delta t*$ une valeur suffisamment petite pour que la modélisation, soit correcte, sans que cela nécessite un nombre déraisonnable de calculs. Heureusement, avec un ordinateur, il est tout a fait envisageable de faire rapidement des dizaines de milliers de calculs en quelques secondes.
Structure de base du programme
Le code ci-dessous a pour objectif de calculer, à chaque intervalle de temps $*\Delta t*$ défini par l’utilisateur les coordonnées de position et des vecteurs accélération et vitesse d’un satellite d’après les conditions initales données, grâce à la méthode d’Euler. L’astre attracteur est situé sur l’origine du repère.
Puis ces coordonnées sont insérées dans le tableau associé à chaque coordonnée.
Enfin on trace dans le graphique la position associée à la date considérée.
Compléter ce code de manière à calculer la distance $*r*$ et les coordonnées des vecteurs $*\vec{a}*$, $*\vec{v}*$ et de position $*x*$ et $*y*$ à chaque boucle.
import matplotlib.pyplot as plt
# Paramètres à choisir ---------------------------------
x0, y0 = 1, 0 # position initiale (U.A.)
vx0, vy0 = 0, 29.79 # vit. initiale (km/s) Terre :29.79
Dt = 1 # intervalle temps (j)
p = 5 # affiche une position sur p
it = 365 # nbre d’itérations de boucle
#-------------------------------------------------------
# Autres constantes
M = 1.989e30 # Masse astre attracteur (kg)
G = 6.6742e-11 # Cste gravitation (S.I.)
# Variables de travail en unités S.I.
x,y = [x0*1.496e11],[y0*1.496e11]
vx,vy = [vx0*1000],[vy0*1000]
ax,ay=[],[]
Dt = Dt*86400
# Mise en forme du graphique
plt.plot(0,0, color='darkorange', marker='o', ms=10)
plt.axis('equal')
lim_axe = max(x0,y0)*2.5e11
plt.axis([-lim_axe, lim_axe, -lim_axe, lim_axe])
plt.grid(True)
# Méthode d’Euler
for i in range(it):
r = ___
ax.append(___)
ay.append(___)
vx.append(vx[i] + ___)
vy.append(vy[i] + ___)
x.append(___) # utiliser la vitesse au rang i+1 pour une meilleure simulation
y.append(___) # utiliser la vitesse au rang i+1 pour une meilleure simulation
if r < ___ : break # on tombe sur le Soleil
# On affiche une position sur p
if i%p == 0 :
plt.plot(x[i],y[i],'bo', ms=1)
plt.pause(0.01)
plt.show()
Version complétée
import matplotlib.pyplot as plt
# Paramètres à choisir ---------------------------------
x0, y0 = 1, 0 # position initiale (U.A.)
vx0, vy0 = 0, 35 # vit. initiale (km/s) Terre :29.79
Dt = 1 # intervalle temps (j)
p = 5 # affiche une position sur p
it = 365 # nbre d’itérations de boucle
#-------------------------------------------------------
# Autres constantes
M = 1.989e30 # Masse astre attracteur (kg)
G = 6.6742e-11 # Cste gravitation (S.I.)
# Variables de travail en unités S.I.
x,y = [x0*1.496e11],[y0*1.496e11]
vx,vy = [vx0*1000],[vy0*1000]
ax,ay=[],[]
Dt = Dt*86400
# Mise en forme du graphique
plt.plot(0,0, color='darkorange', marker='o', ms=10)
plt.axis('equal')
lim_axe = max(x0,y0)*3.5e11
plt.axis([-lim_axe, lim_axe, -lim_axe, lim_axe])
plt.grid(True)
# Méthode d’Euler
for i in range(it): # i varie entre 0 et 364
r = (x[i]**2 + y[i]**2)**0.5
ax.append(-G*M*x[i]/r**3)
ay.append(-G*M*y[i]/r**3)
vx.append(vx[i] + ax[i]*Dt)
vy.append(vy[i] + ay[i]*Dt)
x.append(x[i]+vx[i+1]*Dt)
y.append(y[i]+vy[i+1]*Dt)
if r < 6e7 : break # on tombe sur le Soleil
# On affiche une position sur p
if i%p == 0 :
plt.plot(x[i],y[i],'bo', ms=2)
plt.pause(0.05)
plt.show()
Vérification de la 2e loi de Kepler
On va vérifier si notre simulation permet bien de retrouver la loi des aires. Mais avant… Eh oui, il y deux petits trucs qui doivent être bien clairs.
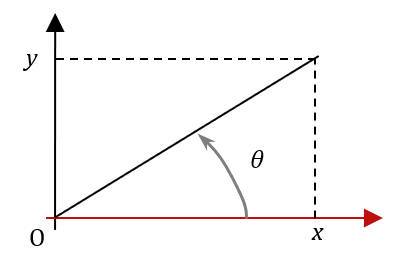
La fonction arctan2(y,x) du module numpy vous renvoie la valeur de $*\theta*$ (en radian) telle qu’illustrée dans le schéma ci-dessous.
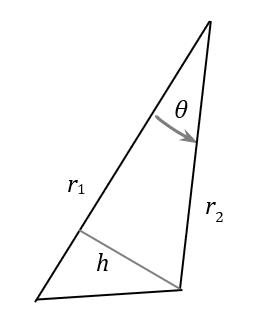
L’aire du triangle ci-dessous est égale à $*r_1·r_2·\frac{\sin \theta}2*$.
Voici la partie du programme qui s’occupe de calculer les aires et de les afficher sur le graphique.
Elle doit être insérée juste avant le plt.show() du programme que vous avez déjà.
Expliquer comment est calculée l’aire balayée par le segment [astre attracteur - satellite].
########################################
# 2e partie, calcul des aires
# Voulez-vous exécuter cette partie ?
afficher = True
#######################################
if afficher :
import numpy as np
import copy
# une aire compte k positions successives
k=50
# on commence à la position j
j=0
# boucle calcul aire + affichage
while j+k < it:
A=0
for i in range (1,k+1):
# calcul de l’aire pour les k position successive
alpha = np.arctan2(y[j+i], x[j+i]) - np.arctan2(y[j+i-1], x[j+i-1])
r0 = np.sqrt(x[j+i]**2 + y[j+i]**2)
r1 = np.sqrt(x[j+i-1]**2 + y[j+i-1]**2)
A += r0*r1*np.sin(alpha)/2
# afficher les aires balayées
# pas obligé, mais c’est joli ☺
X = copy.deepcopy(x[j:k+1+j])
X.insert(0,0)
Y = copy.deepcopy(y[j:k+1+j])
Y.insert(0,0)
plt.fill(X, Y, label='A = ' + '{:.3e}'.format(A) + ' m$^2$')
j+=2*k
plt.legend(loc='lower left')
Vérification de la 3e loi de Kepler
Vérifier que, pour les différentes conditions initiales que vous choisirez (position et/ou vitesse), la 3e loi de Kepler est toujours vérifiée.
Pour cela, à partir de l’animation que vous avez créée, vous déterminerez graphiquement la valeur du demi grand axe $*a*$ et de la période $*T*$ pour deux mouvement différents, et vous vérifierez que la 3e loi est bien validée.
Éléments de correction
Code complet
import matplotlib.pyplot as plt
# Paramètres à choisir -----------------------------------
x0, y0 = 1.5 , 0 # position initiale (U.A.)
vx0, vy0 = 0, 18 # vitesse initiale (km/s) Terre :29.79
Dt = 1 # intervalle temps (j)
p = 5 # affiche une position sur p
it = 365 # nbre d’itérations de boucle
afficher = True # affichage des aires
# Autres constantes
M = 1.989e30 # Masse astre attracteur (kg)
G = 6.6742e-11 # Cste gravitation (S.I.)
#---------------------------------------------------------
# Variables de travail en unités S.I.
x,y = [x0*1.496e11],[y0*1.496e11]
vx,vy = [vx0*1000],[vy0*1000]
ax,ay=[],[]
Dt = Dt*86400
# Mise en forme du graphique
plt.plot(0,0, color='darkorange', marker='o', ms=10)
plt.axis('equal')
lim_axe = max(x0,y0)*2.5e11
plt.axis([-lim_axe, lim_axe, -lim_axe, lim_axe])
plt.grid(True)
# Méthode d’Euler
for i in range(it):
r = (x[i]**2 + y[i]**2)**0.5
ax.append(-G*M/r**3*x[i])
ay.append(-G*M/r**3*y[i])
vx.append(vx[i] + ax[i]*Dt)
vy.append(vy[i] + ay[i]*Dt)
x.append(x[i] + vx[i+1]*Dt)
y.append(y[i] + vy[i+1]*Dt)
if r < 7e8 : break # on tombe sur le Soleil
# On affiche une position sur p
if i%p == 0 :
plt.plot(x[i],y[i],'bo', ms=1)
plt.pause(0.01)
#--------------------------------------------------------------
# Calcul et affichages des aires
if afficher :
import numpy as np
import copy
# Paramètres affichage
k = 30 # une aire compte k positions successives
j = 0 # on commence à la position j
# boucle calcul aire + affichage
while j+k < it:
A=0
for i in range (1,k+1):
# calcul de l’aire pour les k position successive
alpha = np.arctan2(y[j+i], x[j+i]) - np.arctan2(y[j+i-1], x[j+i-1])
r0 = np.sqrt(x[j+i]**2 + y[j+i]**2)
r1 = np.sqrt(x[j+i-1]**2 + y[j+i-1]**2)
A += r0*r1*np.sin(alpha)/2
# afficher les aires balayées
# pas obligé, mais c’est joli ☺
X = copy.deepcopy(x[j:k+1+j])
X.insert(0,0)
Y = copy.deepcopy(y[j:k+1+j])
Y.insert(0,0)
plt.fill(X, Y, label='A = ' + '{:.3e}'.format(A) + ' m$^2$')
j+=2*k
plt.legend(loc='lower left')
plt.show()
À propos de la méthode d’Euler
On utilise vx[i+1] et vy[i+1] et non pas vx[i] et vy[i] pour calculer x[i+1] et y[i+1] sinon, la simulation n’est pas correcte (la planète décrit une spirale qui s’élargit avec le temps).
Ceci est dû au fait que vx[i] et vy[i] sont calculées à partir de ax[i-1] et ay[i-1] elles-mêmes caculées à partir de x[i-1] et y[i-1].
L’erreur commise est donc plus grande car on ferait dépendre directement x[i+1] et y[i+1] de x[i-1] et y[i-1] au lieu de x[i] et y[i].
Calcul de l’aire balayée par le segment astre attracteur - satellite
Cette aire est calculée par approximation, en la découpant en triangles définis par deux positions successives du satellite et par le centre de l’astre attracteur.
Par exemple, si on choisit d’afficher l’aire balayée au cours de 30 positions successives, cette aire est découpée en 30 triangles. On calcule l’aire de chaque triangle et on fait la somme des ces aires de triangles.
Vérification de la 3e loi
On estime la taille du grand axe par lecture graphique (remarquez que, lorsque vous passez la souris sur le graphique, les coordoonnées du pointeur sont affichées – ça permet une lecture graphique un peu plus précise). On ajuste l’intervalle de temps Dt et le nombre d’itérations it de manière à trouver la période orbitale. Puis on vérifie que la 3e loi de Kepler est bien respectée (ce qui est bien le cas).
Satellite PLANCK
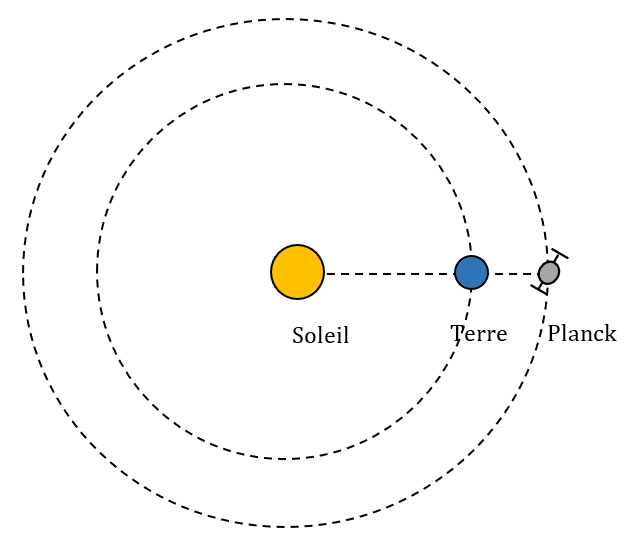
Pour éviter la lumière parasite venant du Soleil, le satellite PLANCK a été mis en orbite de sorte que la Terre se trouve toujours entre le Soleil et le satellite. Les centres du Soleil, de la Terre et le satellite Planck sont toujours alignés.
La période de révolution de la Terre et celle du satellite autour du Soleil sont donc exactement les mêmes : 365 jours.
1. Représenter par un schéma les positions relatives du Soleil, de la Terre et de PLANCK.
2. Montrer, sans calcul, que cette configuration semble en contradiction avec une des lois de Kepler.
3. Proposer une hypothèse permettant de lever cette contradiction.
Correction
1. Schéma montrant les positions relatives du Soleil, de la Terre et de PLANCK (pas à l’échelle)
2. Selon la 3e loi de Kepler, $*T^2/a^3*$ = constante.
Or on nous dit que les centres du Soleil, de la Terre et le satellite Planck sont toujours alignés. Donc ils ont la même période orbitale $*T*$, mais un $*a*$ différents, car la Terre et le satellite Planck ne sont pas à la même distance du Soleil. Ceci est donc en contradiction avec la 3e loi de Kepler.
3. La force gravitationnelle exercée par la Terre sur Planck n’est pas à négliger par rapport à la force exercée par le Soleil, la troisième loi de Kepler ne s’applique donc pas (il s’agit d’un système à trois corps).
Orbite de Hubble
Le télescope spatial Hubble a été lancé en 1990. Il est positionné sur une « orbite basse » à une altitude $*h*$ = 600 km de la surface de la Terre.
On étudie le mouvement de Hubble dans le référentiel géocentrique en négligeant l’interaction gravitationnelle du Soleil avec le télescope.
Données
- Rayon de la Terre : $*R_T*$ = 6380 km
- Masse de la Terre : $*M_T*$ = 6,0·1024 kg
1. Quelle est la trajectoire du télescope Hubble dans ce référentiel ?
2. Montrer que, dans l’approximation d’une trajectoire circulaire, le mouvement du télescope Hubble est uniforme.
3. Établir l’expression de la valeur de la vitesse $*v*$ du satellite dans le référentiel géocentrique.
4. Établir l’expression de sa période de révolution $*T*$ en fonction de $*R_T*$, $*h*$ et $*v*$.
5. Montrer que la troisième loi de Kepler est respectée
6. Calculer la période de révolution $*T*$ du télescope spatial Hubble, exprimée en minutes.
Correction
1. L’altitude du satellite est constante, c’est donc qu’il a un mouvement circulaire dans le référentiel géocentrique.
2. Voir la démonstration du cours.
3. Voir le cours.
4. On sait que $*v = \frac{2\pi(R_T +h)}T*$ d’une part, et que $*v = \sqrt{\frac{GM_T}{R_T+h}}*$ d’autre part. Donc : $µ \begin{aligned} T &= \frac{2 \pi(R_T +h)}{\sqrt{\frac{GM_T}{R_T+h}}} \\ T &= 2 \pi \sqrt{\frac{(R_T +h)^3}{GM_T}} \end{aligned} µ$
5. En élevant $*T*$ au carré, on retrouve bien la 3e loi de Kepler. $µ \begin{aligned} T^2 &= 4 \pi^2 \frac{(R_T +h)^3}{GM_T} \\ \frac{T^2}{(R_T +h)^3} &= \frac{4 \pi^2}{GM_T} \end{aligned} µ$
6. Une bête application numérique : on trouve $*T*$ = 5790 s environ, soit 97 minutes environ.
Révision & entraînement
Ça tourne, Saturne
Cet exercice a été donné en devoir en 2020/2021

La sonde Cassini, lancée en octobre 1997, a été en orbite autour de Saturne entre juillet 2004 et septembre 2017. Son orbite a été modifiée de nombreuses fois, en utilisant principalement l’influence gravitationnelle de Titan, un satellite naturel de Saturne dont la masse est presque deux fois celle de la Lune.
Données
- Masse de Saturne : $*M_S*$ = 5,685·1026 kg
- Constante gravitationnelle : $*G*$ = 6,674·10-11 m3·kg-1·s-2
1. Insertion en orbite de la sonde Cassini
Après un voyage de près de 7 ans, Cassini s’insère en orbite autour de Saturne. Cette première orbite fait évoluer la sonde entre 78 520 kilomètres du centre de Saturne (18 000 kilomètres au-dessus de la couche des nuages) à la périapside (point de l’orbite le plus proche de Saturne) et 9,06 millions de kilomètres à l’apoapside (point de l’orbite le plus éloignée de Saturne).
1.1. Quelle est la forme géométrique de cette orbite ? Quel point particulier de cette forme occupe le centre de Saturne ?
1.2. En utilisant une des lois de Kepler (vous préciserez laquelle) et en vous appuyant sur un schéma, déterminer sur quelle partie de son orbite la vitesse de Cassini est la plus élevée et sur laquelle elle est la moins élevée.
1.3. Quelle est la période de cette orbite ? Exprimer le résultat en jours.
2. Orbite de Titan
L’orbite de Titan autour de Saturne est presque circulaire. Dans cette exercice, on l’assimilera à une orbite circulaire de rayon $*r*$ = 1,22 millions de kilomètres.
2.1. Établir l’expression vectorielle de l’accélération de Titan dans le repère de Frenet.
2.2. Montrer que Titan décrit un mouvement uniforme sur son orbite.
2.3. Établir l’expression vectorielle sa vitesse $*v*$ en fonction de $*M_S*$ et $*r*$.
2.4. Établir l’expression de la période orbitale de Titan et calculer sa valeur en jours.
Correction
1.1. Puisque la distance entre la sonde et le centre de Saturne varie, c’est qu’il s’agit d’une orbite elliptique. Saturne occupe un des foyers.
1.2. Lorsque la sonde est au plus proche de Saturne, le segment qui relie la sonde au centre de Saturne est court. Lorsque la sonde est éloigné, ce segment est grand. Or la loi des aires (2e loi de Kepler) dit que l’aire balayée par ce segment est constante. Donc lorsque le segment est court, la vitesse de la sonde est grande et inversement.
1.3. On utilise la 3e loi de Kepler pour obtenir
$µ T = 2\pi \sqrt{\frac{a^3}{GM_S}} µ$
avec $*a*$ le demi grand-axe de l’ellipse, soit $*a*$ = (78,5·103 + 9,06·106)÷2 = 4,57·106 km
D’où $*T*$ = 9,96·106 s soit environ 115 jours
2.1. La seule force qui s’applique sur Titan est la force d’attraction gravitationnelle $*\vec{F} = \dfrac{GM_S m}{r^2}\vec{u}_n*$ de Saturne.
Donc, d’après la RFD : $*\vec{F} = m\vec{a}*$. Et donc $*\vec{a} = \dfrac{GM_S}{r^2}\vec{u}_n*$
2.2. Voir le cours.
2.3. Comme le mouvement est circulaire uniforme, on a $* a = \dfrac{v^2}r *$ donc $* v= \sqrt{\dfrac{GM_S}r}*$.
Et comme le vecteur vitesse est tangent à la trajectoire, $* \vec{v} = \sqrt{\dfrac{GM_S}r}\vec{u}_t *$
2.4. $* T =\dfrac{2\pi r}v = 2\pi \sqrt{\dfrac{r^3}{GM_S}}*$ = 1,37·106 s soit environ 16 jours.
Envoi d’une sonde vers Mars
Cet exercice a été donné en 2020/2021. D’après le sujet Métropole 2014.
La manière la plus économique en énergie pour se rendre sur Mars consiste à placer la sonde sur une orbite elliptique appelée orbite de transfert. Lorsque celle-ci se trouve sur son orbite de transfert, elle n’est soumise qu’à l’attraction gravitationnel du Soleil.
La sonde commence son voyage interplanétaire lorsque la Terre se trouve à la position T1 correspondant à la périhélie (P – point de l’orbite le plus proche du Soleil) de son orbite. Mars se trouve alors à la position M1 repérée par l’angle α.
Lorsqu’elle arrive à l’aphélie (A – point le plus éloigné du Soleil), elle doit y rencontrer Mars (position M2). La « fenêtre de tir » correspond à la configuration des positions de la Terre et de Mars compatible avec ces conditions.
Les orbites de Mars et de la Terre sont considérées comme circulaires et contenues dans le même plan.
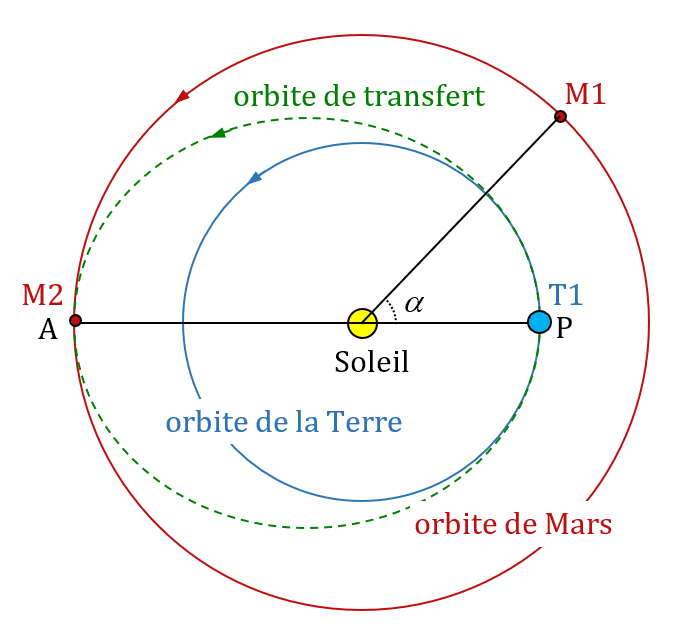
1. Calculer la durée $*\Delta t*$ du voyage de la sonde.
2. Déterminer la valeur de l’angle $*\alpha*$ pour être dans dans la fenêtre de tir.
Données
- Distance Soleil-Terre : $*R_1*$ = 1,50·108 km
- Distance Soleil-Mars : $*R_2*$ = 2,28·108 km
- Période de révolution de Mars autour du Soleil : 1,88 an
- Constante de gravitation universelle : $*G*$ = 6,67×10-11 m3·kg-1·s-2
- Masse du Soleil : $*M_S*$ = 1,99×1030 kg
Correction
1. Le trajet correspond à la moitié de l’ellipse du périhélie à l’aphélie. Le voyage dure donc une demi-période.
On calcule la période grâce à la troisième loi de Kepler :
$µ \frac{T^2}{a^3} = \frac {4π^2}{GM_S} µ$
avec $*a*$ qui vaut $* \dfrac{R_1+R_2}2 = *$ 1,89·108 km.
On trouve $*T*$ = 4,48·107 s soit 519 jours. La durée du voyage correspond à une demi-période, soit environ 259 jours.
2. Il faut chercher quel est le déplacement de Mars sur son orbite en 259 jours.
On sait qu’en 1,88 ans, elle fait 360°, donc en 259 jours elle fait 136°.
Donc $*\alpha*$ = 180 – 136 = 44°.