P8. Circuit RC
Un condensateur est un dipôle capable d’accumuler des charges électriques. Il s’agit d’un constituant élémentaire d’un très grand nombre de circuits électriques ou électroniques (avec la résistance, la bobine, la diode et le transistor). Nous étudierons dans ce chapitre les lois qui régissent son comportement.
Constitution d’un condensateur
- Relier l’intensité d’un courant électrique au débit de charges.
- Citer des ordres de grandeur de valeurs de capacités usuelles.
Un condensateur est constituée de deux plaques conductrices l’une en face de l’autre (d’où son symbole), séparées par un isolant. Lorsqu’on connecte une de ces plaques à la borne ⊕ d’un générateur, et l’autre à la borne ⊖, ces plaques vont se charger. Et le fait qu’elles soient proches l’une de l’autre va permettre d’accumuler des charges dans ces plaques (les charges ⊖ d’une plaque et les charges ⊕ de l’autre s’attirent mutuellement).
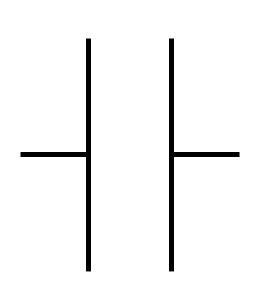
Un condensateur est caractérisé par sa capacité notée $*C*$. Il s’agit de la constante de proportionnalité liant la tension aux bornes d’un condensateur à la charge qu’il a accumulée sur sa plaque ⊕ (la charge sur la plaque ⊖ étant la même, au signe près).
| $*U = \dfrac QC*$ | $*U*$ : tension aux bornes du condensateur $*Q*$ : charge de sa plaque positive (C) $*C*$ : capacité (en farad, noté F) |
Capacité d’un condensateur
On applique une tension de 12 V aux bornes d’un condensateur d’une capacité de 1 µF.
1. Quelle est la charge qu’il a stockée ?
2. Quelle qdm d’électrons cela représente-t-il ?
Charge molaire des électrons : ℱ = 96,5 kC·mol-1.
Correction
1. $*Q = U·C =*$ 12·10–6 C (12 µC)
2. $*n*$ = 12·10-6 ÷ 96,5·103 = 1,24·10-10 = 0,124 nmol
Circuit RC série
- Établir et résoudre l’équation différentielle vérifiée par la tension aux bornes d’un condensateur dans le cas de sa charge par une source idéale de tension et dans le cas de sa décharge.
- Capacité mathématique : résoudre une équation différentielle linéaire du premier ordre à coefficients constants avec un second membre constant.
TP Condensateur
- Identifier et tester le comportement capacitif d’un dipôle.
- Étudier la réponse d’un dispositif modélisé par un dipôle RC.
- Réaliser un montage électrique pour étudier la charge et la décharge d’un condensateur dans un circuit RC.
- Utiliser un oscilloscope.
- Déterminer le temps caractéristique d’un dipôle RC à l’aide d’un oscilloscope.
- Illustrer qualitativement à l’aide d’un oscilloscope, l’effet de la géométrie d’un condensateur sur la valeur de sa capacité.
Mise en évidence de l’accumulation de charge dans un condensateur
- Brancher un bref instant un condensateur aux bornes d’un générateur de 6 V pour qu’il se charge (✋ attention à la polarité).
- Après avoir débrancher le condensateur du générateur, le relier à un circuit série {résistance + LED}
Qu’observe-t-on ? Qu’est-ce que cela montre ?
Charge et décharge d’un condensateur dans un circuit RC série
Un circuit RC série désigne un circuit électrique où sont associés en série un résistor (de résistance $*R*$) et un condensateur (de capacité $*C*$).
- Régler un GBF (générateur basse fréquence) sur une fréquence de l’ordre de quelques dizaines de hertz et sur le mode « tension carrée »
- Visualiser la tension du GBF sur la voie 1 de l’oscilloscope.
- Relier au GBF un circuit RC (la borne ⊖ du condensateur doit être reliée à la borne ⊖ du générateur pour pouvoir visualier correctement la tension à ses bornes sur l’oscilloscope – vous utiliserez le condensateur de 1 µF).
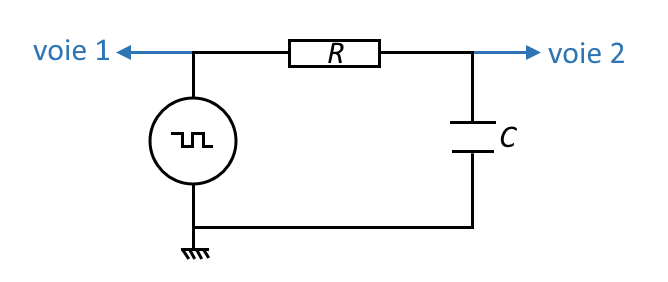
Schéma du montage à réaliser - Visualiser à l’oscilloscope la tension aux bornes du condensateur (en même temps que celle aux bornes du GBF)
Qu’observe-t-on ? Comment peut-on interpréter cette observation ?
- Faites varier la résistance du circuit RC
- Changer de condensateur (prendre celui de 4,7 µF)
Qu’observe-t-on ? Comment peut-on interpréter cette observation ?
On appelle temps caractéristique de charge le temps mis par le condensateur pour se charger à 63 % (on reviendra sur ce point plus tard dans le cours).
- Estimer le temps caractéristique de charge pour trois valeurs différentes de $*R*$ et comparer ce temps au produit $*RC*$ (attention à utiliser les unités S.I.)
Géométrie d’un condensateur
- Remplacer le condensateur par deux feuilles d’aluminium assez grandes (format A5 environ). Vous séparerez ces deux feuilles par une pochette en plastique.
- Choisissez une résistance et une fréquence assez élevées pour qu’on puisse observer la charge de ce « condensateur artisanal »
- Modifier la forme des feuilles d’aluminium et leur surface en regard
Qu’observe-t-on ? Comment peut-on interpréter cette observation ?
Éléments de réponses
Un circuit RC série, c’est l’association en série d’un générateur (idéal de tension), d’une résistance et d’un condensateur.
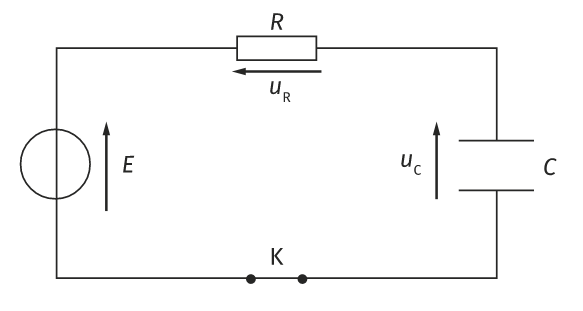
Supposons que le condensateur soit au départ complètement déchargé ($*Q*$ = 0). Lorsqu’on ferme le circuit, un courant se met à circuler. Donc la charge du condensateur augmente et donc la tension à ses bornes augmente.
Du même coup, par la loi d’additivité des tensions (dans ce circuit $*E = U_C + U_R*$), la tension aux bornes de la résistance va diminuer et donc, par la loi d’Ohm, on en déduit que l’intensité du courant va également diminuer.
Autrement dit, la vitesse de charge n’est pas constante. Rapide au début, elle va diminuer au cours de la charge jusqu’à ce que le courant ne circule plus – moment où le condensateur est complètement chargé.
Vous devinez qu’il y a de l’équation différentielle là-dessous… 😁
Équation différentielle de charge
Charge et intensité
Considérons que, pendant une durée très brève $*\mathrm{d}t*$, l’intensité ne varie pas. Alors, la charge $*\mathrm{d}Q*$ gagnée par le condensateur vaudra : $*\mathrm{d}Q = I·\mathrm{d}t*$
On obtient donc un premier résultat très important (qui a d’ailleurs une portée plus générale que simplement la charge ou la décharge d’un condensateur) :
Convention récepteur
Toutes les formules données dans mon cours sous-entendent le choix de la convention « récepteur », c’est-à-dire que le courant est compté positivement lorsqu’il entre dans le condensateur, et négativement quand il en sort.
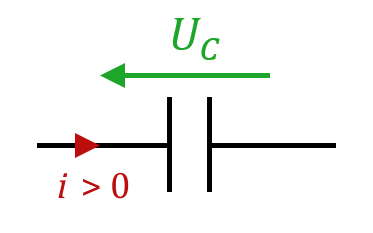
Il est possible de faire le choix inverse, on est alors dans la convention « générateur ». Dans ce cas, on a $µ I = - \frac{\mathrm{d}Q}{\mathrm{d}t} µ$
Charge et tension
D’autre part, on a vu que la loi de fonctionnement du condensateur était $*Q = C·U_C*$. On peut donc en déduire une deuxième relation :
Loi d’additivité des tensions
Aux bornes de la résistance, on a (loi d’Ohm) : $*U_R = R·I*$. De plus, la loi d’additivité des tension permet d’écrire que $*E = U_C + U_R*$ comme on l’a déjà vu plus haut.
En utilisant cette relation et en remplaçant $*U_R*$ par ce qu’on a trouvé avant, on obtient l’équation différentielle : $µ \begin{aligned} E &= U_C + U_R \\ E &= U_C + R·I \\ E &= U_C + RC·\frac{\mathrm{d}U_C}{\mathrm{d}t} \end{aligned} µ$
Rappel
On a vu que la solution générale de l’équation différentielle $µ f'(x) + af(x) = b µ$ était $µ f(x) = Ke^{-ax} + \frac ba µ$On ramène la forme de cette équation différentielle à une forme qui nous est familière : $µ \frac{\mathrm{d}U_C}{\mathrm{d}t} + \frac{U_C}{RC} = \frac{E}{RC} µ$
La solution de cette équation différentielle est : $µ U_C(t) = Ke^{-\frac t{RC}} + E µ$
Si le condensateur est initialement déchargé, on a $*U_C(0) = 0*$ et donc $*K = -E*$. La solution devient : $µ U_C(t) = E·(1-e^{-\frac t{RC}}) µ$
Temps caractéristique de charge
Comme je l’explique dans la partie sur les équations différentielles, la constante $*RC*$ (résistance × capacité) est aussi appelée constante de temps $*\tau*$. Elle s’exprime en seconde (on peut démontrer que ohm × farad = seconde).
On considère généralement par commodité que le condensateur est chargé au bout de $*t = 5·\tau*$.
Tension UC(t) au cours de la charge
L’allure de la courbe représentant la tension $*U_C(t)*$ est la suivante.
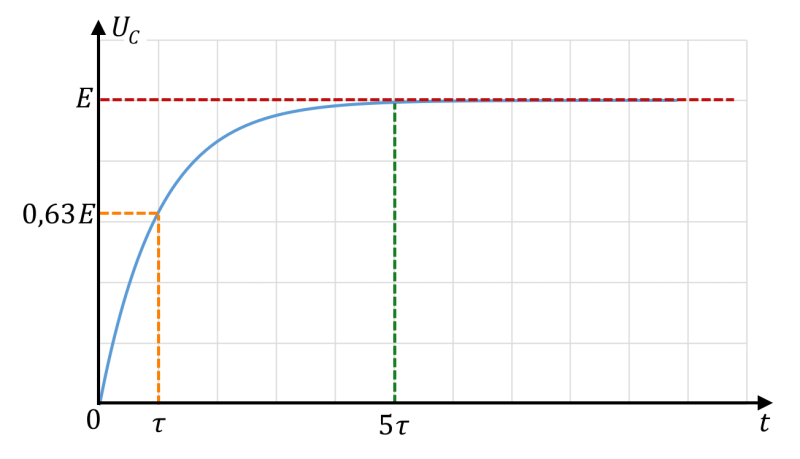
On voit que $*U_C(t)*$ tend vers la tension aux bornes du générateur, et que celle-ci augmente de plus en plus faiblement au cours du temps.
Analogie avec un transfert de gaz
Imaginons un récipient dans lequel règne le vide. Celui-ci est raccordé, par l’intermédiaire d’un tuyau mince, à une pompe P capable de maintenir une pression constante $*P_0*$. Un clapet (en rouge) peut être ouvert instantanément sur commande.
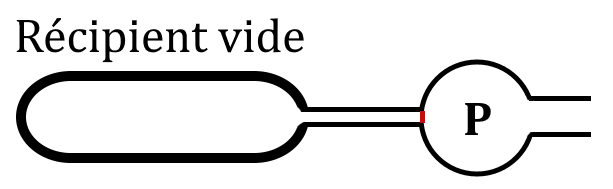
Au moment où le clapet est ouvert, le flux de gaz entrant dans le récipient est maximum, car aucune pression interne dans le récipient ne vient s’opposer à son mouvement.
À mesure que le récipient se remplit, la pression interne augmente et s’oppose au flux de gaz envoyé par la pompe. Le récipient se remplit donc de plus en plus lentement.
Lorsque la pression dans le récipient est égale à la pression $*P_0*$, il n’y a plus de flux de gaz. Le récipient est plein.
La vitesse de remplissage du récipient dépend du diamètre du tuyau (plus le tuyau est fin, plus le remplissage sera lent), mais aussi du volume du récipient. On peut montrer, par contre, que le temps au bout duquel le récipient est plein (c’est-à-dire que sa pression interne est égale à la pression $*P_0*$ fournie par la pompe) ne dépend pas de $*P_0*$.
Dans cette analogie, le volume du récipient correspond à la capacité du condensateur, le tuyau correspond à la résistance (plus il est fin, plus la résistance est élevée) et la pompe correspond au générateur.
Constante de temps
Il est commode d’avoir une idée du taux de charge d’un condensateur initialement déchargé et se trouvant dans un circuit RC au bout d’une durée égale au temps caractéristique $*\tau*$.
Caculer ce taux de charge (pourcentage de charge par rapport à la charge complète) pour un temps $*t = \tau = RC*$.
Correction
Lorsque $*t = \tau*$, on a $* U_C(t) = E·(1-e^{-1}) \simeq 0,63·E*$.
À ce moment, le condensateur est donc chargé à 63 %.
Charge d’un condensateur dans un circuit RC
Autrefois, les dispositifs de déclenchement des essuie-glaces étaient basés sur des circuits RC. Cet exercice vous propose de s’intéresser à cet usage des circuit RC.
On réalise un circuit RC série branché à une batterie de 12 V. La capacité du condensateur vaut $*C*$ = 1,0 mF. Aux bornes du condensateur est également branché un circuit telle que, si $*U_C*$ ≥ 6 V, ce circuit déclenche le balayage des essuie-glaces et vide le condensateur (on ne s’intéresse pas à cette partie du circuit dans cet exercice). Le condensateur se remet en charge dès que les essuie-glaces sont revenus à leur position d’origine.
1. Établir l’équation différentielle qui régit l’évolution de la tension $*U_C*$ aux bornes du condensateur.
2. Résoudre cette équation différentielle.
3. Calculer la valeur de la résistance $*R*$ à placer dans le circuit RC pour que le temps d’immobilisation des essuie-glaces soit de 3 secondes ?
Correction
1. et 2. Voir cours.
3. On veut que $* U_C(3) = 0,5·E*$. Résolution : $µ \begin{aligned} U_C(t) &= E·(1-e^{-\frac t{RC}}) \\ 0,5 &= 1-e^{-\frac t{RC}} \\ e^{-\frac t{RC}} &= 0,5 \\ -\frac t{RC} &= \ln(0,5) \\ R &= - \dfrac t{C·\ln(0,5)} \end{aligned} µ$ En remplaçant $*t*$ par 3 s et $*C*$ par 1,0·10-3 F, on obtient $*R*$ ≃ 4,3 kΩ
Tension UC(t) au cours de la décharge
Si vous avez compris ce qui se passe lors de la charge d’un condensateur dans un circuit RC série, la décharge ne vous posera aucun problème.
Si le condensateur est initialement chargé, lorsqu’on ferme l’interrupteur, on a $*U_R + U_C*$ = 0.
Ceci conduit de manière immédiate à l’équation différentielle qui régit l’évolution de la tension $*U_C(t)*$ au cours du temps :
À partir de là, on procède comme d’habitude : on se ramène d’abord à une forme connue pour trouver la solution de cette équation : $µ \frac{\mathrm{d}U_C}{\mathrm{d}t} + \frac{U_C}{RC} = 0 µ$ d’où la solution : $µ U_C(t) = Ke^{-\frac t{RC}} µ$ Si on note $*U_{C0}*$ la tension initiale aux bornes du condensateur, cette solution s’écrit : $µ U_C(t) = U_{C0}·e^{-\frac t{RC}} µ$
La courbe de décharge ressemble beaucoup à celle de la charge :
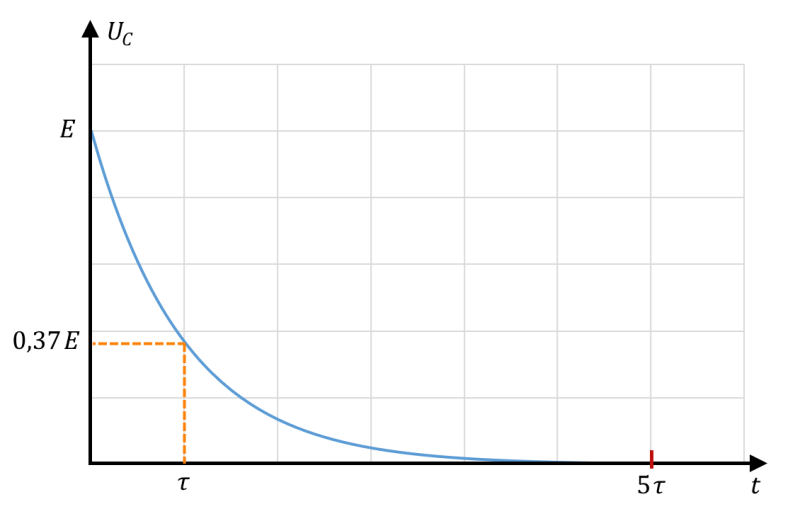
Décharge d’un condensateur
Vous avez peut-être remarqué que sur certains appareils, une petite diode reste allumée encore un certain temps (une ou deux secondes) alors même que l’appareil est débranché. Ceci est dû au fait que certains condensateurs sont chargés au moment où l’appareil est débranché. Ceux-ci se déchargent alors dans la diode, la gardant allumée le temps de la décharger.
Je vous propose dans cet exercice d’étudier un peu cette situation.
On réalise un circuit série dans lequel on connecte un diode électroluminescente (LED), un condensateur et une résistance.
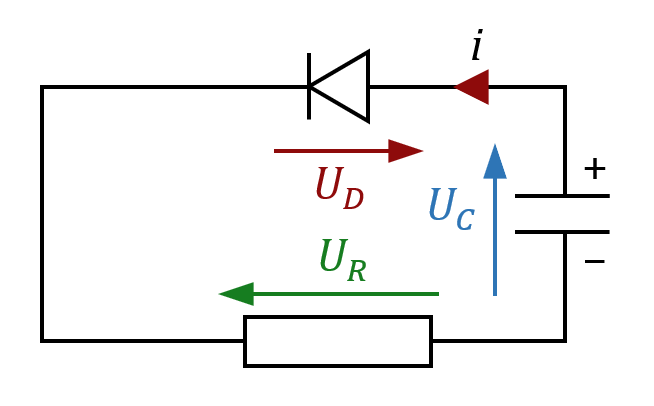
La tension initiale aux bornes du condensateur est de 6,0 V. Sa capacité vaut $*C*$ = 2,0 mF. La résistance à une valeur $*R*$ de 300 Ω.
Lorsqu’elle est passante, la tension aux bornes de la LED vaut 1,1 V quelle que soit l’intensité du courant qui la traverse et sa résistance est négligeable. Elle émet alors de la lumière. Lorsque la tension à ses bornes tombent en dessous de cette valeur (1,1 V), la diode devient bloquante : elle se comporte comme un interrupteur ouvert.
1. En utilisant la loi d’additivité des tensions, trouver la relation entre $*U_C*$, $*U_D*$ et $*U_R*$.
2. Trouver l’équation différentielle qui régit l’évolution de la tension $*U_C*$ au cours du temps lorsque la diode est passante. Donner sa solution.
3. En déduire combien de temps brillera la diode.
4. Le courant dans la diode ne doit jamais excéder 20 mA. Ce circuit électrique met-il en danger la diode ?
Correction
1. $*U_C = U_D + U_R*$
2. On sait que $*U_D*$ = 1,1 V, que $*U_R = RI*$ et que $*U_C = - \frac QC*$ (attention au signe moins ! Ceci est dû au fait qu’on orienté la flèche tension $*U_C*$ dans le même sens que le sens positif de l’intensité.)
On a également que
$µ I = -\dfrac QC µ$
Là encore, remarquez le signe – : le condensateur se décharge, donc la charge diminue au cours du temps et $*\frac {\mathrm{d}Q}{\mathrm{d}t}*$ est négatif. Or, le courant est positif d’après les conventions prises sur le schéma (qui ne sont pas les plus simples, mais qui auront eu le mérite d’attirer votre attention sur ce point. Donc cela implique la présence du signe –.
L’équation différentielle est donc : $µ U_C = U_D - RC·\frac {\mathrm{d}U_C}{\mathrm{d}t} µ$
3. La solution de cette équation différentielle est :
$µ U_C = K·e^{\frac {-t}{RC}} + 1,1 µ$
avec $*K*$ = 6 – 1,1 = 4,9 V.
La diode cesse de briller lorsque la tension aux bornes du condensateur sera égale à la tension de coupure de la diode, soit 1,1 V.
Ceci arrive après un temps $*t = 5·RC = *$ 3 secondes.
4. À $*t*$ = 0, $*U_C*$ = 6 V, $*U_D*$ 1,1 V, donc $*U_R*$ = 4,9 V. On peut donc en déduire l’intensité initiale du courant : $*I = \frac {U_R}R = *$ 4,9÷300 = 16,3 mA.
La diode n’est donc pas en danger.