Incertitudes
En physique (et en ingénierie), il est capital d’estimer l’incertitude associée à toute mesure. Estimer une incertitude peut être très complexe – il s’agit d’un domaine d’ingénierie à part entière (ça s’appelle ingénieur en métrologie). Voici quelques grandes lignes que vous devez savoir à ce propos.
Variabilité de la mesure d’une grandeur physique
- Exploiter une série de mesures indépendantes d’une grandeur physique : histogramme, moyenne et écart-type.
- Évaluer qualitativement la dispersion d’une série de mesures indépendantes.
- Capacité numérique : représenter l’histogramme associé à une série de mesures à l’aide d’un tableur ou d’un langage de programmation.
En sciences, la mesure d’une grandeur (par exemple, d’une masse, d’une température…) est forcément associée à une incertitude expérimentale. Il est impossible d’avoir une mesure d’une précision infinie (on n’est pas en math, on ne manipule pas des nombres « absolus » sans signification physique).
Exemple
Prenons un exemple concret pour bien vous faire sentir le problème. Imaginons que vous vouliez peser un volume d’eau – par exemple pour déterminer la densité de l’eau. Vous disposez de la meilleure balance du monde capable d’une précision infinie ! 😊
Que se passe-t-il pendant votre pesée ? Eh bien il y a une partie de l’eau que vous pesez qui s’évapore. Et peut-être même des substances présentes dans l’air qui se dissolvent (un peu) dans l’eau.
Donc pendant votre pesée, la masse de votre échantillon d’eau n’est pas constante. Certes, sa variation est très faible, mais il est illusoire d’imaginer que vous avez une précision absolue.
Eh bien non ! Car même la masse des solides change (interaction entre la surface et l’environnement, et autres raisons inconnues). N’imaginez pas que j’exagère ! Le problème se pose même avec le PIK.
Le PIK (Prototype International du Kilogramme) est un cylindre constitué d’un alliage de 90 % de platine et 10 % d’iridium (proportions massiques). Depuis 1889 et jusqu’au 20 mai 2019, il a servi à définir le kilogramme – sa masse était égale, par définition, à 1 kg.
Le problème, c’est que la masse du PIK a diminué d’environ 50 µg en un siècle en comparaison de ses copies officielles. La raison de cette divergence n’est pas connue. Ce problème a conduit à une redéfinition du kilogramme à partir des constantes fondamentales de l’Univers (mais c’est une autre histoire).
Bref, il y a déjà un problème rien qu’à cause de la fluctuation inhérente de la grandeur qu’on mesure.
Mais ce n’est pas tout ! 😮 Il est impossible d’avoir une balance (ou un autre instrument de mesure) d’une précision infinie. Et pour plein de raisons.
Ses circuits électroniques ont des caractéristiques qui dépendent de leur température, de leur âge et qui sont elles-mêmes associées à une certaine incertitude. D’autre part, l’intensité de la pesanteur n’est pas la même partout… Cela fait de nombreuses sources d’erreurs, certaines aléatoires, d’autres systématiques (voir paragraphe suivant).
Erreurs aléatoires et erreurs systématiques
Quand on fait une mesure, l’incertitude associée peut provenir de deux types d’erreurs. Les erreurs aléatoires et les erreurs systématiques.
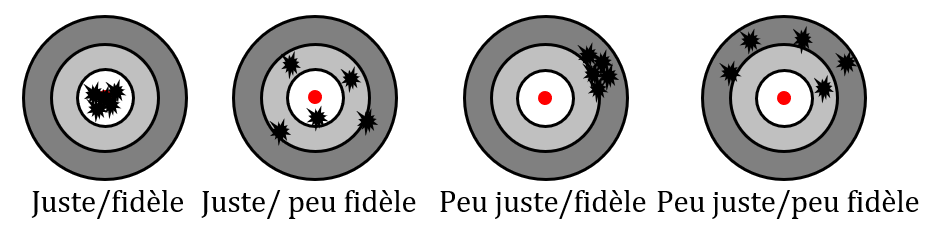
Les erreurs systématiques, dont dépend la justesse de la mesure, se résolvent facilement : il suffit de recalibrer l’appareil de mesure.
Les erreurs aléatoires, dont dépend la fidélité de la mesure, ne peuvent par contre pas être corrigées, puisque justement, elles sont aléatoires… 😁
Mais il faut savoir les estimer pour pouvoir déterminer l’incertitude-type associée à une mesure.
Un appareil de mesure de qualité (donc cher), un savoir-faire certain et un protocole astucieux permettent de minimiser les erreurs aléatoires. On aura l’occasion de s’entraîner sur ces notions au cours des TP et exercices à venir.
Lorsqu’on a une série de mesures d’une même grandeur qui fluctuent légèrement à cause des erreurs aléatoires, on peut quantifier ces erreurs aléatoires en calculant la moyenne des mesures et l’écart-type associé à la série de mesures.
Exemple
Restons sur l’exemple d’une balance. Une balance de qualité supérieure, capable d’afficher une mesure au centième de gramme, peut par exemple avoir une précision garantie de 0,15 % de la masse pesée (c’est ce qu’indiquerait le fabricant dans le manuel de la balance), si celle-ci est bien calibrée.
Ceci signifie que, si on pèse une masse de 5,00 g, la balance sera à ± 0,0075 g (0,15 % de 5,00 g). Elle peut donc afficher n’importe quelle mesure comprise entre 4,99 et 5,01 g (ça dépend de son humeur du moment 😁). Voilà un exemple d’erreur aléatoire.
Maintenant, si on se sert de cette balance en Guyane (où $*g*$ = 9,79 N·kg-1 au lieu de 9,81 N·kg-1 à Paris), comme il y a 0,2 % d’écart entre les valeurs de l’intensité de la pesanteur, on va introduire une erreur systématique de 0,2 % (en moins) sur une mesure faite en Guyane. Il faudra alors recalibrer la balance si on veut éliminer cette erreur systématique.
Variabilité d’une mesure
On a répété plusieurs fois la mesure d’une même masse. Ces mesures sont accessibles dans ce fichier texte.
La première colonne correspond à une première série de mesures, et la deuxième colonne à une autre série de mesures, réalisées différemment (autre balance, par exemple).
Pour apprécier la variabilité de ces séries de mesures, on trace un histogramme (ou « graphique statistique ») sur un tableur.
1. Créer un histogramme pour chacune des séries de valeurs données. Ajuster les paramètres du graphique de manière à obtenir les graphiques ci-dessous.
Vous pouvez notamment définir le nombre de catégories (et donc de barres) dans les paramètres liés à l’axe des abscisses.
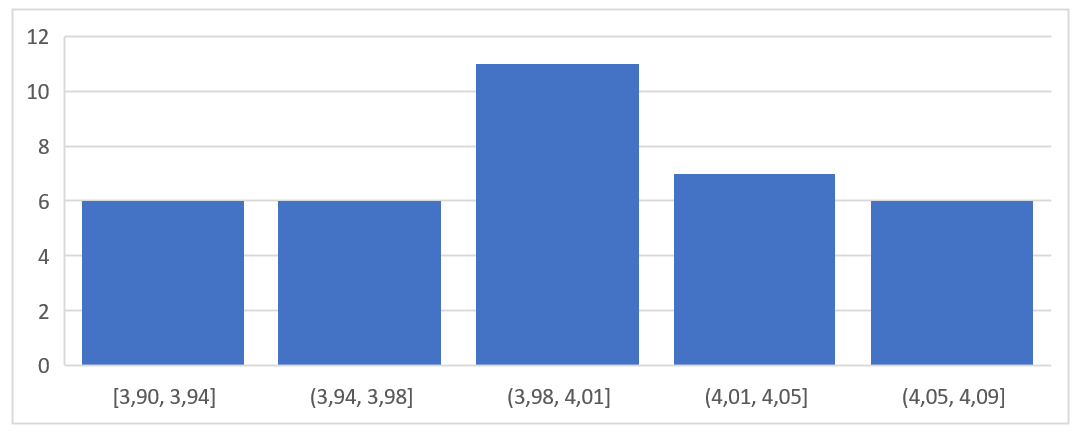
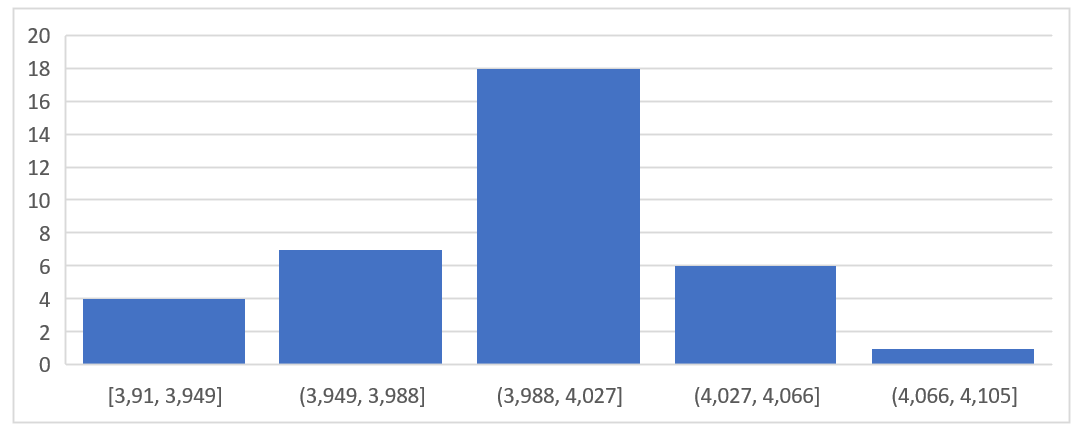
2. D’après ces graphiques, quelle est la série de mesures qui a la plus grande dispersion ?
On peut quantifier la dispersion d’une série de mesures en calculant l’écart-type de la série de mesures (c’est-à-dire une sorte d’« écart moyen » entre une valeur de la série prise au hasard et la moyenne de la série de mesure).
3. Calculer la moyenne et l’écart-type de chacune des séries de mesures. Quelle est la série de mesures qui paraît la plus fidèle ?
4. Ces deux séries de mesures vous paraissent-elles justes ?
Correction
Incertitudes
- Définir qualitativement une incertitude.
- Discuter de l’influence de l’instrument de mesure et du protocole.
- Procéder à l’évaluation d’une incertitude par une approche statistique (évaluation de type A).
- Procéder à l’évaluation d’une incertitude par une autre approche que statistique (évaluation de type B).
- Évaluer, à l’aide d’une formule fournie, l’incertitude d’une grandeur s’exprimant en fonction d’autres grandeurs dont les incertitudes-types associées sont connues.
En sciences, le résultat d’une mesure n’est (dans l’idéal) jamais une simple valeur. Il est toujours donné sous la forme $*m \pm u(m)*$ associé à un niveau de confiance. $*m*$ est appelé le mesurande (c’est la valeur lue sur l’appareil de mesure) et $*u*$ signifiant uncertainty.
Par exemple, si on indique que $*m*$ = 4,0 g ± 0,1 g avec un niveau de confiance de 95 %, cela signifie que le résultat de cette mesure nous permet d’affirmer qu’il y a 95 % de chance que $*m*$ soit compris dans l’intervalle [3,9 ; 4,1].
Incertitudes absolues et relatives
Une incertitude peut être exprimée de manière absolue, c’est-à-dire de manière indépendante de la valeur mesurée. Par exemple, lorsqu’on utilise un instrument gradué (une règle, une burette…), on considère généralement que l’incertitude absolue correspond à une demie graduation.
Quand on mesure une longueur $*\ell*$ avec une règle, on a donc une incertitude $*u(\ell)*$ = 0,5 mm. Et ce quelle que soit la valeur de $*\ell*$.
Mais une incertitude absolue est peu parlante quant à la précision de la mesure. Est-on précis si on fait une mesure de distance à ± 0,5 mm ? Eh bien ça dépend… Si vous mesurez la longueur d’une piscine, oui, c’est précis (et même illusoirement précis, car il y a d’autres sources d’incertitude, mais on en reparlera plus tard).Par contre, si vous mesurez la taille d’une fourmi, ça na va pas être précis du tout.
C’est pour ça qu’on préfère souvent exprimer une incertitude de manière relative, c’est-à-dire sous forme d’un pourcentage de la valeur mesurée.
0,5 mm d’incertitude, rapporté à une mesure de 5 mm , ça fait 10 % d’incertitude. Pas de quoi être particulièrement fier de la précision de cette mesure. 😏
Par contre, 0,5 mm rapporté à une mesure de 1 m, ça fait 0,05 %. C’est déjà plus intéressant… 😊
Incertitude de type A
Les incertitudes de type A sont évaluées à partir d’une série de mesure, en utilisant les outils statistiques. Il existe des formules vous permettant de calculer une incertitude de type A à partir de l’écart-type associé à une série de mesure, du nombre de mesures effectuées et du degré de confiance que vous souhaitez avoir dans votre résultat.
Ces formules sont de la forme : $µ u(x) = \frac{k \sigma(x)}{\sqrt{n}} µ$ avec $*\sigma(x)*$ l’écart-type de la série de mesure de la grandeur $*x*$, $*n*$ le nombre de mesure effectuées et $*k*$ un facteur qui dépend du degré de confiance que vous souhaitez avoir dans votre résultat.
✋ Pas de panique ! Vous n’avez rien à savoir par cœur, ces formules vous seront fournies et explicitées si vous devez y faire appel. Vous devez, par contre, savoir calculer rapidement un écart-type.
Incertitude de type B
Ce type d’incertitude se calcule à partir d’une mesure unique. Et ce n’est pas quelque chose de facile. En fait, il y a une bonne part d’estimation « au doigt mouillé » (c’est-à-dire un peu au pifomètre). On peut regrouper les sources d’erreurs en deux grandes catégories :
- Précision de l’instrument : elle est généralement fournie par le constructeur. Mais l’instrument est souvent moins précis que ça, à moins de le faire recalibrer régulièrement et/ou de respecter les conditions d’utilisation (notamment la température de mesure indiquée).
- Précision de l’expérimentateur : elle dépend non seulement de son expérience, mais aussi de la pertinence du protocole suivi. Elle s’estime, à notre niveau, « à la louche ».
Pour la lecture sur un instrument gradué, on considère que l’incertitude de lecture correspond à la moitié de la plus petite graduation.
Pour la lecture sur un instrument digital, on considère que l’incertitude de lecture correspond à la moitié du rang du dernier chiffre affiché.
Estimer une incertitude de pesée
Un élève souhaite peser une masse de 0,50 g de $*\ce{NaCl}*$ avec une balance qui affiche jusqu’au centième de gramme. Il pose une coupelle de 0,70 g sur la balance, puis il fait la tare et enfin il prélève le $*\ce{NaCl}*$. Il renverse quelques grains de sel sur le plateau par maladresse (ces grains sont pesés, mais ils ne sont pas récupérés – ils représentent au maximum 0,01 g, peut-être moins.). Le constructeur garantit une précision de la pesée à 0,5 %, mais la balance n’a pas été étalonnée depuis longtemps et on considère que sa précision est deux fois moins bonne (1 %).
1. Faire la liste de toutes les sources d’incertitudes en donnant leur valeur (absolue ou relative, celle qui est la plus directe à obtenir).
2. En déduire l’incertitude absolue et relative sur la masse de $*\ce{NaCl}*$ pesée (tenir compte de la tare de 0,70 g due à la coupelle).
3. Même question pour une masse $*m*$ = 5,0 g.
Correction
1. Liste des incertitudes
• Précision balance : 1 % (relative)
• Maladresse : 0,01 g (absolue)
• Affichage digital : 0,005 g (absolue)
2. Incertitude absolue
• Précision balance : 1 % de 1,2 g = 0,012 g
• Maladresse : 0,01 g
• Affichage digital : 0,005 g
Incertitude absolue totale : 0,027 g
Incertitude relative
0,027 g = 5,4 % de 0,5 g. Précision peu satisfaisante
3. Incertitude absolue = 0,057 (1 % de 5,7 g) + 0,01 + 0,005 = 0,072 g
Incertitude relative : 0,072 g = 1,44 % de 5 g. La précision est bien meilleure.
Incertitude composée (Tale)
Lorsqu’on calcule une grandeur à partir de grandeurs expérimentales (par exemple l’énergie cinétique à partir de la masse et de la vitesse), l’incertitude relative portant sur la grandeur calculée est appelée incertitude composée et elle se calcule à partir des incertitudes relatives des grandeurs expérimentales.
L’incertitude relative $* \frac {\Delta a}a*$ d’une grandeur $*a*$ qui se calcule à partir des grandeurs mesurées $*b*$, $*c*$, $*d*$ et $*e*$ par la relation : $µ a = \frac{bc^2}{de^3} µ$ vaut : $µ \frac {\Delta a}a = \sqrt{\left(\dfrac {\Delta b}b\right)^2 + 2 \left(\dfrac {\Delta c}c\right)^2 + \left(\dfrac {\Delta d}d\right)^2 + 3 \left(\dfrac {\Delta e}e\right)^2} µ$
Par exemple, si on veut calculer l’incertitude relative sur une énergie cinétique d’un objet, sachant que l’on connaît la masse $*m*$ de cet objet à 1 % près et la vitesse $*v*$ de cet objet à 3 % près, le calcul est le suivant : $µ u(E_c) = \sqrt { u(m)^2 + 2×u(v)^2} = \sqrt { 0,01^2 + 2×0,03^2} = 0,043 µ$
On obtient donc une incertitude de 4,3 %
Parce que dans la formule de l’énergie cinétique, la vitesse est élevée au carré. Si on a un grandeur à la puissance $*n*$, que ce soit au numérateur ou au dénominateur, il faut multiplier sa contribution à l’incertitude composée par $*n*$. Des facteurs de valeur fixe (par exemple le facteur ½ dans la formule de l’énergie cinétique) n’ont aucune influence sur l’incertitude composée, car ce sont des nombres et non pas des mesures. Ils n’ont donc aucune incertitude.
Estimer une qdm de gaz parfait
Un récipient de volume $*V*$ = 100 mL ± 0,1 mL contient un gaz considéré comme parfait, à une pression $*P*$ = 1009 hPa ± 3 hPa. Sa température est de 23 °C ± 0,5 °C. La constante des gaz parfait vaut $*R*$ = 8,31446 J·mol-1·K-1
Calculer la qdm de gaz contenu dans ce récipient. Donner l’incertitude relative et absolue sur cette valeur.
Correction
$* n = \cfrac{PV}{RT} = *$ 4,099826 mmol
Calcul de l’incertitude relative sur $*n*$ : $µ \begin{aligned} \cfrac {u(n)}n &= \sqrt{ \cfrac{u(P)}P +\cfrac{u(V)}V +\cfrac{u(T)}T} \\ &= \sqrt{ \cfrac{3}{1009} +\cfrac{0,1}{100} +\cfrac{0,5}{23+273}} \\ &= 0,0036 \end{aligned} µ$ Cette incertitude vaut 0,36 %.
$*n*$ = (4,099826 ± 0,0146) mmol ou 4,099826 mmol ± 14,6 µmol
Remarque : on écrira cette valeur avec un nombre de chiffres significatifs dans l’exercice suivant. Pour l’instant, on la laisse comme ça.
Écriture du résultat et valeur de référence
Chiffres significatifs
Les chiffres significatifs permettent souvent de se passer de la notation $*x \pm u(x)*$. C’est une manière commode, quoique moins précise, de donner une indication sur le degré de précision avec lequel on connaît la grandeur dont on parle.
Par exemple, si on écrit qu’une masse $*m*$ vaut 1,0 kg, on indique qu’on la connaît avec une incertitude de 0,05 kg (la moitié du rang du dernier chiffre significatif – ici le 10e de kg).
Par contre, si on écrit que $*m*$ vaut 1,00 kg, l’incertitude n’est plus que de 0,005 kg.
Lorsque, pour des raisons de précision, on doit tout de même faire figurer l’incertitude $*u(x)*$, il faut écrire $*x*$ avec un nombre pertinent de chiffres significatifs.
Par exemple, écrire $*x*$ = 1,2548723 ± 0,12 n’a pas de sens. En effet, l’incertitude ici est telle que les derniers chiffres de la valeur apportent une précision qui n’a en fait aucun sens. On ne donne pas une masse au µg près quand l’incertitude de mesure est de l’ordre de 100 g… 😏
La règle est d’adapter le nombre de chiffres significatifs à l’incertitude. Dans l’exemple ci-dessus, on écrirait $*x*$ = 1,25 ± 0,12.
Vous lirez souvent que l’incertitude doit être exprimée avec un seul chiffre significatif, arrondi au supérieur. Par exemple une incertitude de 0,12 deviendrait 0,2.
Ce n’est pas une règle absolue. Tout dépend de l’incertitude sur l’incertitude. 😅
Si vous avez estimé assez grossièrement cette incertitude, alors oui, un seul chiffre significatif est de rigueur. Ici, le résultat de la mesure deviendrait $*x*$ = 1,3 ± 0,2. Mais si vous avez fait une estimation plus fine de votre incertitude, et que vous avez confiance dans cette estimation, vous pouvez garder deux chiffres significatifs sur cette incertitude.
Chiffres significatifs
Exprimer le résultat trouvé dans l’exercice sur le gaz parfait avec un nombre correct de chiffres significatifs.
Correction
On avait trouvé $*n*$ = (4,099826 ± 0,0146) mmol ou 4,099826 mmol ± 14,6 µmol
Si on décide de garder 2 chiffres significatifs pour l’incertitude : $*u(n)*$ = 15 µmol.
Le dernier chiffre des incertitudes correspond au rang des µmol, donc on arrondit le résultat au rang des µmol.
$*n*$ = (4,100 ± 0,015) mmol ou 4,100 mmol ± 15 µmol
Si on décide de garder 1 chiffre significatif pour l’incertitude : $*u(n)*$ = 2 µmol. Rappelez-vous, on arrondit toujours l’incertitude au supérieur.
Le dernier chiffre des incertitudes correspond au rang des dizaines de µmol, donc on arrondit le résultat au même rang.
$*n*$ = (4,10 ± 0,02) mmol
Comparer à une valeur de référence
Pour valider une mesure, il est parfois possible de comparer cette mesure à une valeur de référence. Imaginons qu’en TP, vous ayez déterminé la vitesse de propagation du son. Vous avez trouvé $*c*$ = 329 m·s-1. La valeur théorique attendue vaudrait, dans les conditions de votre expérience, 343 m·s-1. Pouvez-vous valider votre mesure ? C’est-à-dire pouvez-vous dire « ma mesure est bien en accord avec le résultat attendu » ?
Eh bien, ça dépend ! 😁 L’écart entre la valeur attendue et la valeur expérimentale est de 4,1 %. Si votre incertitude est de 5 % par exemple, alors oui, votre mesure est bien valide, car la marge d’erreur (4,1 %) est inférieure à l’incertitude (5 %). Mais si au contraire, vous avez estimé votre incertitude de mesure à 1 % au maximum, alors il y a un problème quelque part… 😊
Et il faudra donc creuser le sujet.