P3. Mouvement d’un système
L’étude des mouvements et de leurs causes (les forces) est une branche de la physique appelée « Mécanique ». Ce domaine de la physique est très important aussi bien en ingénierie qu’en physique fondamentale (astronomie, physique des particules)
Dans ce chapitre, vous aller avoir une première approche de la mécanique. On reviendra largement dessus en terminale.
Préalables
Quelques définitions pour fixer les idées.
Système
Lorsqu’on étudie un mouvement, il faut clairement définir le système que l’on étudie. Le système, c’est l’objet, ou l’ensemble d’objets reliés entre eux, dont on étudie le mouvement.
Par exemple, on peut étudier le mouvement du système Terre-Lune autour du Soleil. Ce n’est pas le même que le mouvement du système Lune autour du Soleil.
Référentiel
Vous savez, depuis la sixième, qu’un mouvement est « relatif ». Le mouvement d’un système ne peut être étudié que par rapport à un autre objet, qu’on appelle un référentiel. Dans la vie courante, le référentiel que l’on choisit le plus souvent, parfois de manière inconsciente, c’est le référentiel terrestre, c’est-à-dire le sol.
- terrestre (le sol) ;
- géocentrique (centre de la Terre) ;
- héliocentrique (centre du Soleil) ;
Eh bien, c’est soit l’exercice qui vous l’indique, soit vous qui le choisissez. Dans ce cas, il est important que vous explicitiez bien quel référentiel vous avez choisi.
Repère
La position d’un point est définie par ses coordonnées. Et qui dit coordonnées dit … repère.
Un repère, c’est un système d’axes (3 au maximum) gradués et une origine.
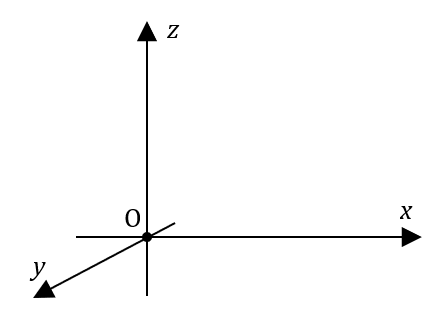
Eh bien parce que l’Univers possède 3 dimensions d’espace. Donc si vous voulez définir la position d’un point, il vous faut trois coordonnées, que l’on note généralement $*x*$, $*y*$ et $*z*$.
Mais, bonne nouvelle, on étudiera, au lycée, seulement des mouvements rectilignes et des mouvements plans. Dans une trajectoire rectiligne, le mouvement du système se fait selon une droite. Du coup, si vous choisissez bien votre repère, il n’y a qu’une seule coordonnée qui varie. On peut donc choisir un repère avec un seul axe (parce que sur les deux autres, les coordonnées du système sont constantes).
Et dans le cas d’une trajectoire plane, si vous choisissez bien votre repère, il n’y a que deux coordonnées qui varient, donc… je vous laisse deviner la suite. 😊
Référentiel et repère
On souhaite étudier la trajectoire d’un ballon lancé par un joueur de basket.
1.a. Quel référentiel est-il pertinent de choisir ?
1.b. Quel repère est-il pertinent de choisir ?
2. Quel est le mouvement d’un objet fixé au sol dans le référentiel géocentrique ?
Correction
1.a. Il faut choisir le référentiel terrestre (ça n’aurait aucun sens d’étudier le mouvement du ballon par rapport au joueur, car celui-ci peut être en mouvement pendant le déplacement du ballon.
1.b. Pour ce qui est du repère, on oriente son axe horizontal dans le sens du déplacement du ballon, de manière à ce que la partie « horizontale » du déplacement ne se fasse que selon cet axe. On évite ainsi d’avoir trois coordonnées pour repérer le ballon. Deux suffisent.
2. L’objet décrit un cercle dont le centre est traversé perpendiculairement par l’axe de rotation de la Terre.
Position
Bon, alors pour la suite du chapitre, il va falloir être à l’aise avec les vecteurs. 😏
La position d’un point dans un repère, c’est tout simplement ses coordonnées.
Si on appelle M le point matériel dont on étudie le mouvement, la position du point M peut s’écrire : ($*x*$ ; $*y*$ ; $*z*$). Et comme je vous le disais juste avant, on sera toujours dans une situation où au moins une des coordonnées ne change jamais au cours du mouvement. On pourra donc tout simplement ne pas en tenir compte.
Trajectoire d’un objet en mouvement
Imaginons un objet en mouvement, par exemple un ballon de basket, l’objet étant assimilé à un point. Sa trajectoire correspond aux positions qu’il occupe à différents instants du mouvement, dans un repère donné.
Vecteur vitesse
Définition et construction
La vitesse est une grandeur vectorielle. En effet, indiquer la valeur de la vitesse ne suffit pas à complètement décrire cette vitesse. Il faut encore indiquer dans quelle direction (et sens) l’objet se déplace.
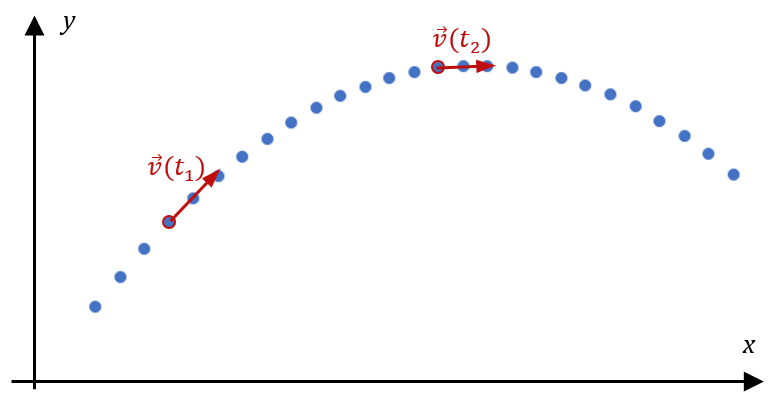
Le vecteur vitesse de cet objet, à un instant donné, est un vecteur dont la direction et le sens indiquent le sens de déplacement du point et dont la norme correspond à la valeur de sa vitesse.
La taille des vecteurs vitesse sur le schéma dépend de l’échelle de représentation choisie et n’est pas importante. C’est leur taille relative qui est importante : on voit que $*\vec{v}(t_2)*$ est plus petit que $*\vec{v}(t_1)*$, car le ballon se déplace moins vite en haut de sa trajectoire qu’au moment où il est lancé.
Valeur de la vitesse
La valeur approchée ou moyenne de la vitesse d’un objet parcourant une distance $*d*$ pendant une durée $*\Delta t*$ est donnée par : $µ v_{moy}= \frac{d}{\Delta t} µ$
Si la vitesse est constante pendant la durée $*\Delta t*$, alors la vitesse moyenne est égale à la vitesse instantanée (c’est-à-dire la vitesse exacte à un instant précis) à tout instant. Si la vitesse varie au cours du mouvement, la vitesse moyenne est une approximation de la vitesse instantanée, qui est d’autant plus proche de celle-ci que $*\Delta t*$ est petit.
Coordonnées du vecteur vitesse
Lorsqu’un mobile se déplace d’une position A ($*x_A*$ ; $*y_A*$) à une position B ($*x_B*$ ; $*y_B*$) pendant un temps $*\Delta t*$, les coordonnées du vecteur « vitesse moyenne » $*\vec{v}_{moy}*$ sont : $µ \vec{v}_{moy} \begin{pmatrix} \dfrac {x_B - x_A}{\Delta t} \\ \dfrac {y_B - y_A}{\Delta t} \end{pmatrix} µ$
Représentation d’un vecteur vitesse
Imaginons un bille se déplaçant horizontalement à vitesse constante en ligne droite, à la vitesse de 2,0 cm·s-1.
1. Représenter quatre positions successives de cette bille espacée de 2,0 secondes, à l’échelle 1:1 (taille réelle).
2. Représenter, pour ces quatre positions, le vecteur vitesse à l’échelle 0,5 cm pour 1 cm·s-1, puis à l’échelle 1 cm pour 1 cm·s-1.
Correction
En vert : vecteur vitesse à l’échelle 0,5 cm·s-1 → 1 cm
En rouge : vecteur vitesse à l’échelle 1 cm·s-1 → 1 cm
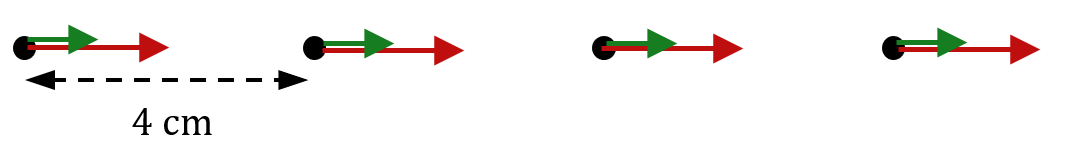
Variation de vitesse et accélération
- Exploiter une vidéo ou une chronophotographie d’un système modélisé par un point matériel en mouvement pour construire les vecteurs variation de vitesse. Tester la relation approchée entre la variation du vecteur vitesse entre deux instants voisins et la somme des forces appliquées au système.
- Capacité numérique : utiliser un langage de programmation pour étudier la relation approchée entre la variation du vecteur vitesse d’un système modélisé par un point matériel entre deux instants voisins et la somme des forces appliquées sur celui-ci.
- Capacité mathématique : Sommer et soustraire des vecteurs.
Vecteur variation de vitesse
Le vecteur variation de vitesse $*\Delta \vec{v}*$ entre deux instants $*t_1*$ et $*t_2*$ est la différence entre $*\vec {v}(t_2)*$ et $*\vec{v}(t_1)*$ : $*\Delta \vec{v} = \vec {v}(t_2) - \vec{v}(t_1)*$
Si cette différence est nulle, alors le vecteur vitesse $*\vec{v}*$ ne varie par entre ces deux instants. Plus $*\Delta \vec{v}*$ est grand, plus $*\vec{v}*$ varie, en norme et/ou en direction-sens.
Principalement la partie « Additionner et soustraire des vecteurs ».
TP Variation du vecteur vitesse
Objectif : à partir d’une vidéo d’un mouvement parabolique, tracer le vecteur variation de vitesse $*\Delta \vec{v}*$ au cours du mouvement grâce à un programme en Python.
Je ne vous cache pas que l’objectif de ce TP est ambitieux et que pour l’atteindre, vous allez devoir apprendre pas mal de chose. Mais vous êtes là pour ça, non ? 😊
Pointage de la vidéo
• Télécharger la vidéo que nous allons exploiter, puis réalisez le pointage vidéo de la balle sur Regressi (voir le tuto sur cette page).
✋ Attention : ne pointez la balle que si elle n’a pas de contact ni avec les mains de la joueuse, ni avec le panier.
Modélisation de la trajectoire dans Excel
• Exporter vos données ($*t*$, $*x*$ et $*y*$) vers Excel, puis afficher le graphique montrant la trajectoire du ballon, c’est-à-dire $*y*$ en fonction de $*x*$.
Remarquez que la trajectoire présente des petites imperfections dues à l’imprécision du pointage. Nous allons corriger ces imperfections en modélisant $*x(t)*$ et $*y(t)*$ à partir des valeurs expérimentales du pointage.
• Afficher le graphique $*x(t)*$, puis modéliser ce graphique en y ajoutant une courbe de tendance.
• Afficher l’équation de cette courbe de tendance sur le graphique. Vous disposez maintenant de l’équation mathématique liant $*x*$ à $*t*$.
• Calculer, dans une nouvelle colonne, pour chaque $*t*$, la valeur modélisée de $*x*$ à partir de l’équation mathématique déterminée précédemment.
• Faite pareil pour $*y(t)*$
Ces valeurs modélisées « lissent » les imperfections de la courbe.
Tracer un vecteur en Python
En vous aidant des explications données dans la rubrique Python de mon site, afficher une figure qui montre :
- Un vecteur $*\vec{v}*$ de coordonnées (1 ; 0,5) partant du point de coordonnées (0 ; 0)
- Un vecteur $*\vec{w}*$ partant de l’extrémité de $*\vec{v}*$ allant jusqu’à (2 ; 2,5)
- Le vecteur $*\vec{v} + \vec{w}*$ partant du point (0 ; 0)
- Le vecteur $*\vec{v} - \vec{w}*$ partant du point (0 ; 0)
Trajectoire du ballon sur Python
1. Importer les valeurs du pointage dans un programme Python
La première étape du programme, c’est d’importer les valeurs du pointage $*t*$, $*x*$ et $*y*$ dans un format que Python comprend. Pour ça, on va utiliser la fonction txt2list que vous trouverez dans la rubrique Python : Importer un fichier txt de colonnes de valeurs.
À la fin de cette étape, vous aurez une liste contenant 3 éléments, qui eux-mêmes sont des listes : la liste des valeurs de $*t*$, la liste des valeurs de $*x*$ et la liste des valeurs de $*y*$
2. Afficher la trajectoire
Voir dans la rubrique Python : Graphique simple.
Vecteur vitesse
Le vecteur « vitesse moyenne » entre deux positions successive (appelées dans l’ordre (1) et (2)) de la balle s’écrit : $µ \vec{v} \begin{pmatrix} \dfrac {x_2 - x_1}{\Delta t} \\ \dfrac {y_2 - y_1}{\Delta t} \end{pmatrix} µ$
Mais si vous l’affichez tel quel sur la représentation de la trajectoire du ballon, ces vecteurs vitesses seront très grands. Il faut donc changer d’échelle, en divisant les coordonnées du vecteur vitesse par un nombre bien choisi, de manière à ce que ce vecteur vitesse ne soit ni « trop grand », ni « trop petit ».
• Écrire le programme qui va tracer au point $*i*$ le vecteur vitesse qui correspond à la vitesse moyenne entre les positions $*i*$ et $*i+1*$. Ce programme doit comporte une boucle for (voir tuto Python) pour tracer le vecteur vitesse pour tous les points de la trajectoire (sauf le dernier).
Variation du vecteur vitesse
Nous allons maintenant afficher les variations du vecteur vitesse. Par exemple, pour la position 1, la variation du vecteur vitesse $*\Delta \vec{v}_1*$ vaut $*\vec{v}_1 - \vec{v}_0*$. On obtient donc que : $µ \Delta \vec{v}_1 \begin{pmatrix} \dfrac {x_2 - x_1}{\Delta t} - \dfrac {x_1 - x_0}{\Delta t} \\ \dfrac {y_2 - y_1}{\Delta t} - \dfrac {y_1 - y_0}{\Delta t} \end{pmatrix} µ$
On obtient après simplification : $µ \Delta \vec{v}_1 \begin{pmatrix} \dfrac {x_2 - 2x_1 + x_0}{\Delta t} \\ \dfrac {y_2 - 2y_1 + y_0}{\Delta t} \end{pmatrix} µ$
• Écrivez une boucle qui permet d’afficher tous les vecteurs variation de vitesse au cours du mouvement.
Que constate-t-on à propos de ces vecteurs ?
Éléments de correction
Vous trouverez dans ce fichier le résultat du pointage de la vidéo, au format txt, après modélisation sur Excel
Code pour afficher la variation du vecteur vitesse
import matplotlib.pyplot as plt
t = [0.36, 0.4, 0.44, 0.48, 0.52, 0.56, 0.6, 0.64, 0.68, 0.72,
0.76, 0.8, 0.84, 0.88, 0.92, 0.96, 1.0, 1.04, 1.08, 1.12,
1.16, 1.2, 1.24, 1.28, 1.32, 1.36]
x = [0.296, 0.474, 0.653, 0.832, 1.011, 1.189, 1.368, 1.547,
1.726, 1.904, 2.083, 2.262, 2.441, 2.62, 2.798, 2.977,
3.156, 3.335, 3.513, 3.692, 3.871, 4.05, 4.228, 4.407,
4.586, 4.765]
y = [2.475, 2.688, 2.886, 3.068, 3.235, 3.387, 3.524, 3.645,
3.752, 3.843, 3.918, 3.979, 4.025, 4.055, 4.07, 4.07,
4.054, 4.024, 3.978, 3.917, 3.841, 3.749, 3.643, 3.521,
3.384, 3.231]
plt.plot(x, y, 'ko', ms = 5)
for i in range(len(x)-1):
plt.arrow(x[i], y[i], (x[i+1]-x[i])/0.4, (y[i+1]-y[i])/0.4,
length_includes_head=True, head_width=0.05,
color='CornflowerBlue')
if i > 0 :
plt.arrow(x[i], y[i], (x[i+1]-2*x[i]+x[i-1])*20, (y[i+1]-2*y[i]+y[i-1])*20,
length_includes_head=True, head_width=0.05,
color='DarkRed')
plt.axis('equal')
plt.show()
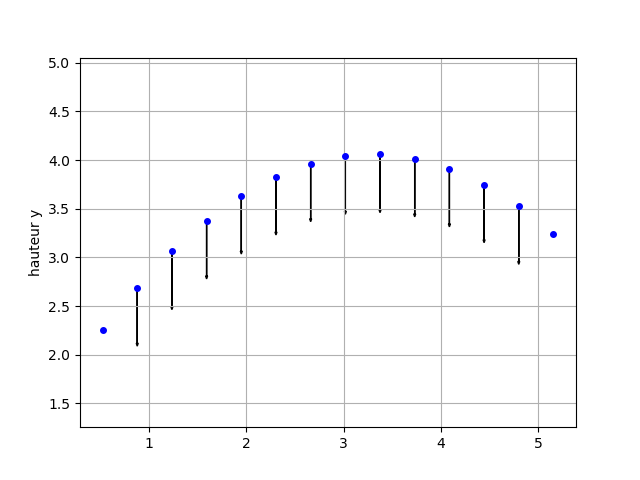
Graphique obtenu
Activité notée – Modélisation
À partir du fichier Excel, en utilisant la feuille qui vous est destinée :
- Modéliser $*x(t)*$ et $*y(t)*$. Vous devez faire apparaître ces deux modélisations sur un graphique, avec l’équation des courbes de tendance.
- Calculer $*x'(t)*$ et $*y'(t)*$ d’après les modèles dans deux nouvelles colonnes.
- Renvoyez-moi le fichier Excel par mail.
Au cours du TP précédent, on a pu constater que le vecteur variation de vitesse, au cours du mouvement de la balle, a le même sens et la même direction que la seule force qui s’exerce sur lui, à savoir son poids. Ce n’est bien sûr pas un hasard… 😊
Accélération moyenne
De la même manière qu’on a vu le vecteur « vitesse moyenne » un peu plus haut, on peut définir le vecteur « accélération moyenne » : $µ \vec{a}_{moy} = \frac{\Delta \vec{v}_{moy}}{\Delta t} µ$
Son unité est m/s/s soit m/s2 ou m·s-2.
Si au temps $*t*$, le vecteur vitesse est $*\vec{v}_1*$ et au temps $*t + \Delta t*$, le vecteur vitesse est noté $*\vec{v}_2*$, on a la relation approchée : $µ \vec{v}_2 = \vec{v}_1 + \vec{a}_{moy}·\Delta t µ$
Voici trois situations particulières.
| Situation | Signification |
|---|---|
 |
$*\vec{v}*$ et $*\vec{a}*$ ont même sens et même direction : l’objet se déplace en ligne droite à une vitesse croissante. |
 |
$*\vec{v}*$ et $*\vec{a}*$ ont la même direction mais un sens opposé : l’objet se déplace en ligne droite à une vitesse décroissante. |
 |
$*\vec{v}*$ et $*\vec{a}*$ sont orthogonaux : l’objet tourne dans le sens indiqué par $*\vec{a}*$ à vitesse constante |
Bien comprendre la notion d’accélération
Il est important que vous compreniez bien ici la différence entre le sens du terme « accélération » en physique et dans la vie courante.
Dans la vie courante, on dit qu’un objet « accélère » lorsque la valeur de sa vitesse augmente. Ceci ne correspond qu’à la première situation présentée où $*\vec{v}*$ et $*\vec{a}*$ ont même sens et même direction.
Le sens de l’accélération en physique est beaucoup plus large. On dit qu’un objet accélère lorsque son vecteur vitesse change au cours du temps. Donc dès qu’un objet n’est pas immobile ou qu’il n’est pas en mouvement rectiligne uniforme, son vecteur accélération n’est pas nul.
Et plus la variation du vecteur vitesse est importante au cours du temps, plus le vecteur accélération sera important.
Lois de Newton
- Utiliser la relation $* \sum \vec{F}_{ext} = m\vec{a} *$
Somme des forces extérieures appliquées à un système
Lorsqu’un système est soumis à plusieurs forces extérieures, la somme vectorielle des forces auxquelles il est soumis – que l’on appelle aussi la résultante des forces – est la somme de tous les vecteurs forces.
Par force extérieure, on entend une force exercée par quelque chose qui ne fait pas partie du système. Si on s’intéresse à un bateau à voile, par exemple, la force que le vent exerce sur la voile est une force extérieure. Mais la force que la voile exerce sur le mât n’est pas une force extérieure, car le mât et la voile sont tous les deux des parties du système considéré, à savoir le bateau.
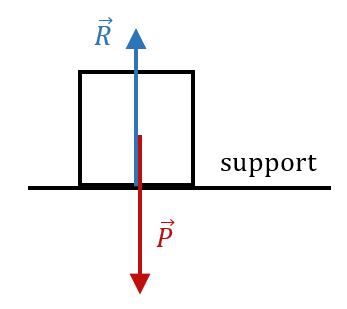
Dans l’exemple ci-dessus, il y a deux forces extérieures qui s’appliquent sur l’objet : son poids $*\vec{P}*$, exercé par la Terre, et la réaction $*\vec{R}*$ du support sur lequel il est posé. Ici la somme des forces $* \sum \vec{F}_{ext}*$ représente $*\vec{P} + \vec{R}*$.
$*\vec{P} = m\vec{g}*$ avec $*\vec{g}*$ le champ de pesanteur, d’intensité $*g*$ = 9,8 n·kg-1, de direction verticale et de sens vers le bas.
1e loi de Newton – Principe d’inertie
Cette loi a été vu en seconde :
Lorsque $*\sum \vec{F}_{ext} = \vec{0}*$, on dit que les forces extérieures se compensent. On dit aussi que le système est isolé (si aucune force ne s’exerce sur lui) au pseudo-isolé si ces forces se compensent.
Palet de curling
Un palet de curling glisse selon une trajectoire rectiligne, sans perdre de vitesse.

1. Quelles forces s’exercent sur le palet ?
2. Que peut-on dire de la résultante de ces forces ?
Correction
1. Son poids et la réaction de la glace.
2. L’énoncé précise que le palet a un mouvement rectiligne uniforme. On en déduit que la résultante des forces est nulle.
2e loi de Newton – Relation Fondamentale de la Dynamique (RFD)
La somme vectorielle des forces appliquées sur un objet de masse $*m*$ lui communique une accélération $*\vec{a}*$ vérifiant la relation :
Pour utiliser rigoureusement cette relation, il faut faire appel à des notions mathématiques que nous verrons l’année prochaine.
Alors, attention ! 😊 Sous son apparente simplicité, cette loi est extrêmement puissante ! 😎
Mais elle nécessite d’être rigoureux lorsqu’on l’utilise. On va voir ci-dessous un exemple détaillé de son utilisation. Ça va vous prendre un certain temps de l’assimiler, mais passer du temps pour comprendre à fond cet exemple, ça en vaut la peine.
Mouvement d’une luge sur un plan incliné
La situation
Un enfant descend une pente enneigé avec sa luge. La pente fait un angle $*\alpha*$ = 10° avec l’horizontale. La luge et l’enfant ont une masse totale $*m*$ et l’intensité du champ de pesanteur $*g*$ sera prise égale à 10 N·kg-1. On considère que les forces de frottement sont négligeables.
Notre objectif
Prévoir la vitesse de la luge après 3 secondes de glisse, la vitesse de la luge à $*t*$ = 0 étant nulle.
1ère étape : poser la situation
Avant toute chose, on fait un schéma. En physique, les schémas, c’est tout simplement indispensable ! 😑
Sur ce schéma, on place le système qu’on étudie {luge + enfant}, les forces qui s’exercent sur le système et un repère.
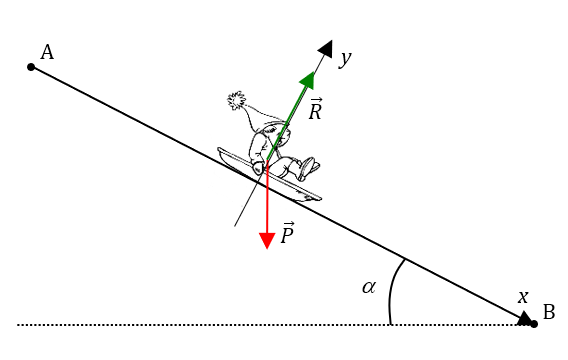
2e étape : expliciter les coordonnées des vecteurs-force
Si on néglige les frottements, il y a deux forces seulement qui s’exercent sur le système. Son poids, et la réaction du sol. Le poids est toujours vertical vers le bas (donc perpendiculaire à la droite en pointillés qui représente l’horizontale). La réaction du support est toujours perpendiculaire au support (ceci a été vue en seconde).
Les coordonnées de $*\vec{R}*$ sont faciles à trouver : l’abscisse de $*\vec{R}*$, notée $*R_x*$ est nulle (parce que ce vecteur est perpendiculaire à l’axe $*\mathrm{O}x*$) et son ordonnée est positive et sa valeur est égale à la norme de $*\vec{R}*$, notée $*R*$ (on la calculera plus tard).
Pour $*\vec{P}*$, c’est un peu plus délicat. Il faudra utiliser un peu de trigo… 😅
Un petit zoom sur la figure s’impose.
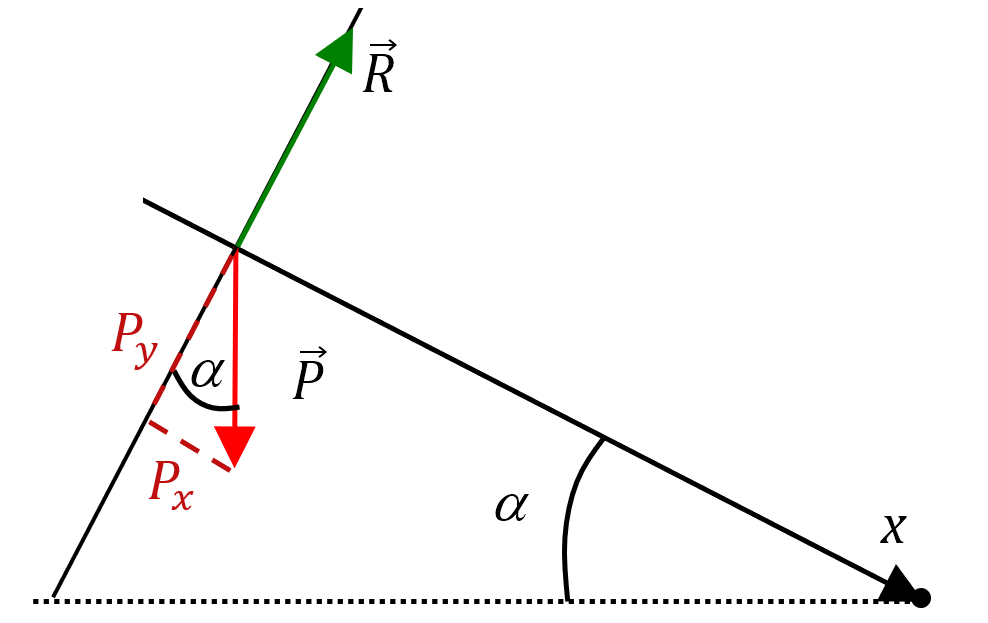
L’angle $*\alpha*$ se retrouve également entre le $*\vec{P}*$ et l’axe $*\mathrm{O}y*$. Du coup, l’abscisse de $*\vec{P}*$ vaut $*P_x = P·\sin \alpha*$. Elle est positive car $*\vec{P}*$ pointe vers les $*x*$ positifs. Je rappelle que $*P*$ est la notation pour la norme de $*\vec{P}*$.
L’ordonnée de $*\vec{P}*$ est négative (car $*\vec{P}*$ pointe vers les $*y*$ négatifs) et vaut $*P_y = -P·\cos \alpha *$
Si vous avez eu du mal à suivre, n’hésitez pas à relire la première partie de la page sur les vecteurs. Normalement, c’est du niveau seconde au maximum. 😏
Calculer les coordonnées du vecteur accélération grâce à la RFD
Dans la situation qu’on étudie, $*\sum \vec{F}_{ext}*$ c’est tout simplement $*\vec{P} + \vec{R}*$. Donc la RFD appliquée à notre situation nous permet d’écrire : $µ \vec{P} + \vec{R} = m\vec{a} µ$
Mais on ne peut rien faire de plus avec cette relation vectorielle. Il faut l’exprimer sur chacun des axes, avec les coordonnées correspondantes : $µ \begin{aligned} P_x + R_x &= ma_x \\ P_y + R_y &= ma_y \end{aligned} µ$
En partant du constat que la luge ne quitte pas le sol, et donc qu’elle n’a pas de mouvement selon l’axe $*\mathrm{O}y*$, on peut en déduire que $*a_y*$ = 0
Donc, on obtient, grâce à la relation sur l’axe $*\mathrm{O}y*$ : $µ -P \cos \alpha + R = 0 µ$
Et grâce à la relation sur $*\mathrm{O}x*$ : $µ P \sin \alpha + 0 = ma_x µ$
Ça y est ! 😅 On a les coordonnées du vecteur accélération !
$µ \vec{a} \begin{pmatrix} \begin{aligned} a_x &= g \sin \alpha \\ a_y &= 0 \end{aligned} \end{pmatrix} µ$
On peut maintenant faire le calcul : $*a_x*$ = 10×sin(10°) = 1,7 m·s-2.
Chaque seconde, la vitesse de la luge augmente de 1,7 m·s-1. Donc au bout de 3 secondes, cette vitesse vaut 3×1,7 ≃ 5 m·s-1.
Référentiel galiléen
Le principe d’inertie et la RFD ne s’appliquent que dans des référentiels galiléens. Qu’est-ce qu’un référentiel galiléen ? C’est un référentiel dans lequel la RFD peut s’appliquer. 😊
Oui ! On tourne en rond. 🔄
Je vais vous donner un exemple pour mieux vous faire sentir les choses et vous faire comprendre pourquoi la définition d’un référentiel galiléen tourne en rond. Imaginez une balle posée sur une surface parfaitement horizontale, dans une voiture. La balle est initialement immobile, donc d’après le principe d’inertie ($* \sum \vec{F}_{ext} = \vec{0} \Leftrightarrow *$ système immobile ou en MRU), la résultante des forces qui s’appliquent sur elle (son poids et la réaction du support) est nulle. Si la voiture se met à accélérer (dans le sens commun du terme), la balle va se mettre en mouvement vers l’arrière de la voiture. Et pourtant aucune nouvelle force n’est apparue sur la balle. Cette mise en mouvement est uniquement due à l’accélération de la voiture. On a ici un exemple de situation où la RFD ne s’applique pas. Le référentiel de la voiture est non galiléen.
Ce qu’il faut retenir
- La RFD (et le principe d’inertie) ne se vérifient que dans un référentiel galiléen.
- Le référentiel terrestre peut être considéré comme galiléen pour des mouvements localisés.
- Un référentiel en MRU par rapport à un référentiel galiléen est lui aussi galiléen.
- Un référentiel dont le vecteur accélération n’est pas nul par rapport à un référence galiléen n’est pas galiléen.
Accélération de la Tesla Roadster
La Tesla Roadster peut passer de 0 à 100 km/h en 3,9 s. Sa masse vaut $*m*$ = 1358 kg à vide.

1.a. Dans la situation où la voiture passe de 0 à 100 km·h-1 en ligne droite, que peut-on dire du sens et de la direction du vecteur accélération par rapport au vecteur vitesse ?
1.b. Calculer la valeur de son accélération moyenne en 3,9 s.
2.a. Quelles forces s’appliquent sur la voiture ? On négligera les forces de frottements.
2.b. Donner la valeur de la force motrice qui s’applique à cette voiture lors de ce mouvement. On considère qu’elle emporte avec elle un conducteur de 75 kg.
3. Quel temps mettrait-elle pour passer de 0 à 100 km/h si elle transporte 2 personnes de 75 kg ?
Correction
✋ Attention, passer des vecteurs aux valeurs nécessite une grande rigueur ! Soyez bien attentifs, dans cette correction, aux justifications des calculs effectués.
1.a. En supposant que la voiture accélère en ligne droite, le vecteur accélération $*\vec{a}*$ et le vecteur vitesse $*\vec{v}*$ ont même sens et même direction, car sa vitesse augmente et elle se déplace en ligne droite.

1.b. On a vu que $*\vec{a} = \dfrac{\Delta \vec{v}}{\Delta t} = \dfrac{\vec{v}_f-\vec{0}}{\Delta t} = \dfrac{\vec{v}_f}{\Delta t} *$ avec $* \vec{v}_f *$ la vitesse finale de la voiture, de valeur 100 km/h.
On a vu à la question précédente que $*\vec{a}*$ et $*\vec{v}*$ ont même sens et même direction.
On définit un vecteur unitaire $*\vec{u}*$ colinaire à $*\vec{v}*$ et de même sens. On a alors :
$µ a·\vec{u} = \dfrac{v_f·\vec{u}}{\Delta t} µ$
Donc
$µ a = \frac{v_f}{\Delta t} µ$
On convertit $*v_f*$ en m·s-1 : $*v_f*$ = 100÷3,6 ≃ 27,8 m·s-1.
Donc $*a*$ = 27,8÷3,9 = 7,1 m·s-2.
2.a. Son poids $*\vec{P}*$, la réaction de la route $*\vec{R}*$ et la force motrice $*\vec{F}*$.
2.b. Il y a deux forces verticales : $*\vec{P}*$ et $*\vec{R}*$ et une force horizontale $*\vec{F}*$.
Or la voiture ne bouge pas sur un axe vertical (elle ne tombe pas et ne s’envole pas). Donc on peut en déduire que $*\vec{P} + \vec{R} = \vec{0}*$
Donc, dans la situation de la voiture, $*\sum{\vec{F}_{ext}} = \vec{F}*$.
Ceci nous permet d’écrire que $*\vec{F} = m\vec{a}*$. Et comme ces deux vecteurs ont même direction et même sens (car $*m*$ >0), on a : $*F=ma*$.
Donc $*F*$ = (1358+75)×7,1 ≃ 10,2·103 N.
3. L’accélération de la voiture avec deux personnes dedans vaut $*a = \dfrac Fm = *$ 10,2·103 ÷ (1358 + 2×75) ≃ 6,8 m·s-2.
Grâce à la relation $* \vec{v}_f = \vec{a}·\Delta t + \vec{v}_i *$, sachant que $*\vec{v}_i = \vec{0}*$ et en utilisant le même vecteur unitaire $*\vec{u}*$ que précédemment, on obtient la relation : $* v_f·\vec{u} = a·\vec{u}·\Delta t *$, ce qui donne
$µ \Delta t = \frac {v_f}{a} µ$
Il faut maintenant 27,8÷6,8 ≃ 4,1 s pour atteindre les 100 km/h.
Distance de freinage
Exercice à faire avec un tableur.
On peut lire sur un site de sécurité routière que la distance de freinage d’une moto lancée à 90 km/h vaut à peu près 50 m.
On considère le système {moto + conducteur} pesant $*m*$ = 300 kg. Sa force de freinage maximale vaut $*F*$ = 1870 N.
1. Sur un schéma, représenter la moto par un point, puis représenter le vecteur vitesse et le vecteur accélération moyenne sans vous soucier de l’échelle (seuls la direction et le sens sont importants).
2. Vérifier que sa distance d’arrêt vaut bien environ 50 m en calculant, tous les 10e de seconde, sa vitesse et la distance parcourue pendant cet intervalle de temps.
Correction
1. Schéma

2. Pour répondre à cette question, il faut utiliser un tableur. Dans une colonne, on va mettre le temps écoulé depuis le début du freinage, tous les 10e de seconde. Dans la colonne suivant, on va mettre la valeur de la vitesse (en m·s-1). Et dans la 3e colonne, on va calculer la distance $*d*$ parcourue pendant le 10e de seconde en cours. Avant tout calcul, votre fichier doit ressembler à ceci :
| $*t*$ (s) | $*v*$ (m·s-1) | $*d*$ (m) |
|---|---|---|
| 0 | 25 | 0 |
| 0,1 | ||
| 0,2 | ||
| 0,3 | ||
| 0,4 | ||
| … |
Ensuite, on se sert de la formule que nous avons vu plus haut : $* \vec{v}_2 = \vec{v}_1 + \vec{a}·\Delta t *$
On définit un vecteur unitaire $*\vec{u}*$ de même direction et de même sens que $*\vec{v}*$.
Comme $*\vec{a}*$ et $*\vec{v}*$ ont des sens opposés, alors $*\vec{a} = -a·\vec{u}*$, et cette relation devient, après simplification par $*\vec{u}*$ :
$µ v_2 = v_1 -a·\Delta t µ$
$*a = \frac Fm =*$ 1870÷300 = 6,23 m·s-2.
Donc pour calculer la vitesse à $*t*$ = 0,1 s, on prend la vitesse à $*t*$ = 0 et on enlève $*a·\Delta t*$ = 6,23×0,1 = 0,623 m·s-1.
Et on répète cette opération jusqu’à ce que $*v*$ soit le plus proche de 0 possible.
Pour calculer la distance parcourue pendant chaque intervalle de 0,1 s, on a envie d’utiliser la relation $*d = v·t*$… 😊.
Mais quelle valeur de $*v*$ choisir ? La vitesse change tout au long de l’intervalle de temps. Par exemple, entre $*t*$ = 0 et $*t*$ = 0,1 s, la vitesse passe de 25 m·s-1 à 24,377 m·s-1. Quelle valeur choisir ? Si on prend 25 m·s-1, on surestime la vitesse. Si on prend 24,377 m·s-1, on la sous-estime. Le mieux, dans le cadre de ces calculs approximatifs, c’est de prendre un moyenne des deux (24,689 m·s-1).
C’est la « moins mauvaise » solution. On verra une autre manière de faire, plus rigoureuse, en classe de terminale.
Donc, pour calculer $*d*$ à $*t*$ = 0,1 s, on fait (25 + 24,377)÷2×0,1 = 2,469 m.
Et on répète le calcul, en étirant la formule, jusqu’à la date pour laquelle la moto est arrêtée.
Il ne reste plus qu’à faire la somme de toutes ces distances pour connaître la distance totale nécessaire pour que la moto s’arrête.
Voici le fichier Excel que vous devriez obtenir.
Révision & entraînement
Décollage de l’A330
Un avion de ligne moyen porteur tel que l’Airbus A330 a les caractéristiques suivantes : masse maximale au décollage $*m*$ = 200 tonnes ; poussée des réacteurs $*F*$ = 2×310 kN ; vitesse de décollage v = 270 km/h. On négligera les forces de frottement.
1.a. Faire un bilan des forces s’exerçant sur l’avion au cours de cette phase de décollage.
1.b. Calculer son accélération.
1.b. Calculer le temps nécessaire au décollage de l’avion.
2. Avec un tableur, calculer la distance nécessaire au décollage.
Correction
1.a. Bilan des forces extérieures qui s’appliquent sur l’avion : son poids $*\vec{P}*$, la réaction du sol $*\vec{R}*$, la force de poussée des réacteurs notée $*\vec{F}*$ (et aussi des forces de frottements que l’on négligera par la suite).
1.b. Calcul de l’accélération à partir de la 2e loi de Newton :
Sur l’axe vertical, l’avion n’a pas de mouvement (il n’est pas encore en train de s’élever dans les airs), donc $*\vec{P}*$ et $*\vec{R}*$ se compensent.
Dans la situation étudiée, la somme des forces extérieures se résume à $* \vec{F}*$.
La RFD s’écrit ici : $* \vec{F} = m\vec{a}*$
Comme $*\vec{F}*$ et $*\vec{a}*$ ont le même sens, la relation vectorielle $* \vec{F} = m\vec{a}*$ implique la relation en valeurs $*F = ma*$, ce qui permet d’en déduire la valeur de l’accélération : $*a*$ = $*F*$÷$*m*$ = (2×310·103)÷(200·103) = 3,1 m·s2.
1.c. Tout au long du mouvement, $*\vec{v}*$ et $*\vec{a}*$ ont le même sens. Donc la relation vectorielle $* \vec{v}_2 = \vec{v}_1 + \vec{a}_{moy}·\Delta t *$ implique la relation en valeurs $* v_2 = v_1 + a_{moy}·\Delta t *$.
Et comme l’accélération est constante, $*a_{moy}*$ = $*a*$ = 3,1 m·s2.
La vitesse initiale est nulle, donc on arrive enfin à la relation qui nous intéresse : $* v_2 = a·\Delta t *$.
On sait que $*v_2*$ doit valoir 270 km/h soit 75 m/s, donc $*\Delta t*$ = 75÷3,1 = 24 s.
L’avion met environ 24 secondes à décoller.
2. On programme le tableur pour calculer la distance parcourue pendant un temps $*\Delta t*$. Au lieu de prendre $*v(t)*$, on peut prendre la moyenne entre $*v(t)*$ et $*v(t+\Delta t)*$, l’erreur commise est moins importante (comme dans l’exercice sur le freinage de la moto).
Vous prenez un $*\Delta t*$ assez petit (0,1 s, par exemple), et vous trouvez une distance de décollage d’environ 900 m.
Chute verticale d’une pierre
On laisse tomber un caillou dans un puit. On néglige les frottements de l’air.
1. Faire un bilan des forces s’exerçant sur le caillou.
2. Donner la direction et le sens du vecteur accélération. Calculer la valeur de son accélération. Dépend-elle de la masse du caillou ?
3. Donner les caractéristiques du vecteur vitesse du caillou en fonction du temps.
Correction
1. Sur le caillou ne s’exerce que le poids $*\vec{P}*$.
2. L’accélération est verticale vers le bas, comme le poids.
2e loi de Newton : $* \sum \vec{F}_{ext} = \vec{P} = m\vec{a}*$ or $*\vec{P}=m\vec{g}*$, donc $*\vec{a} = \vec{g}*$.
On sait que $*g*$ = 9,8 m·s-2 donc $*a*$ = 9,8 m·s-2.
On voit que $*a*$ ne dépend pas de la masse de l’objet. Il est intéressant de retenir ce résultat : l’accélération d’un objet sous l’effet de son poids ne dépend pas de sa masse !
3. $*\vec{v}_2 = \vec{v}_1 + \vec{a}_{moy}·Δt*$. Ici, la vitesse initiale est nulle, l’accélération est constante, et la vitesse et l’accélération ont le même sens, donc $*v=a·Δt*$.
Le vecteur vitesse sera vertical vers le bas, et sa valeur vaut : $*v = 9,8t*$.
Accélération d’une voiture
Cet exercice a été donné en devoir en 2020/2021
On donne ci-dessous les performances d’une voiture telles qu’on peut les trouver sur sa fiche technique.
| Vitesse maxi | 140 km/h |
|---|---|
| 0 à 50 km/h | 3,6 s |
| 0 à 100 km/h | 9,5 s |
| 80 à 120 km/h | 7,1 s |
1.a. Calculer l’accélération moyenne de la voiture entre 0 et 50 km/h puis entre 0 et 100 km/h. Peut-on considérer que l’accélération est constante entre 0 et 100 km/h ?
1.b. Calculer son accélération moyenne entre 50 et 100 km/h.
2. Le schéma ci-dessous montre trois positions de la voiture : la première à $*t*$ = 0 où la voiture est à l’arrêt, la seconde à $*t*$ = 1 s puis la troisième à $*t*$ = 2 s. Représenter sur ce schéma le vecteur vitesse $*\vec{v}_1*$ à $*t*$ = 1 s et le vecteur$*\vec{v}_2*$ à $*t*$ = 2 s, à l’échelle 1 cm pour 2 m·s-1.

3. Donner les caractéristiques (direction, sens, valeur) du vecteur variation de vitesse $*\Delta \vec{v}*$ entre les dates $*t*$ = 1 s et $*t*$ = 2 s.
4. Quelle sont les forces qui s’exercent sur la voiture ? Que vaut $* \Sigma \vec{F}_{ext}*$ dans cette situation ? Justifier en vous appuyant sur la réponse à la question précédente.
5. La voiture pèse 1420 kg avec son conducteur. En utilisant la relation approchée de la deuxième loi de Newton, estimer la valeur moyenne de la force motrice de la voiture entre 0 et 50 km/h.
Correction
1.a. Comme $*\vec{v}*$ et $*\vec{a}*$ ont le même sens et que la vitesse initiale est nulle, on peut écrire $*v = a_{moy}·\Delta t*$, donc :
- $*a_{moy}*$ = 50÷3,6÷3,6 = 3,86 m·s-2 pour l’accélération de 0 à 50 km/h
- $*a_{moy}*$ = 100÷3,6÷9,5 = 2,62 m·s-2 pour l’accélération de 0 à 100 km/h
Ces deux valeurs sont différentes, donc l’accélération n’est pas constante de 0 à 100 km/h.
1.b. De 50 à 100 km/h, $*\vec{v}*$ et $*\vec{a}*$ ont le même sens, on peut écrire $*v_2 = a_{moy}·\Delta t + v_1*$ avec $*v_2*$ = 100 km/h soit 27,8 m·s-1 et $*v_1*$ = 13,9 m·s-1. Donc $*a_{moy} = \dfrac {v_2 - v_1}{\Delta t}*$ = 2,35 m·s-1
2. La valeur de l’accélération moyenne est de 3,86 m·s-2 (parce qu’au bout de deux secondes, la voiture n’a pas encore atteint 50 km·h-1, donc on prend la première valeur calculée à la question 1.a.
Ça signifie qu’au bout d’une seconde, la vitesse de la voiture est de 3,86 m·s-1 et au bout de deux secondes, sa vitesse est de 2×3,86 = 7,72 m·s-1.
À l’échelle indiquée, le premier vecteur vitesse (à $*t*$ = 1 s), doit mesurer 3,86÷2 ≃ 1,9 cm. Et le deuxième doit être deux fois plus grand.
Schéma des vecteurs vitesse
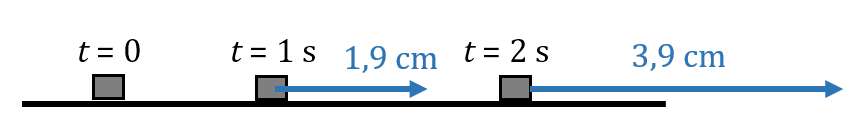
3. Direction et sens : horizontal vers l’avant.
Norme : $*\vec{v}_2*$ et $*\vec{v}_1*$ ont même sens et même direction, donc $* \Delta v = v_2 - v_1 *$ = 3,86 m·s-1
4. Forces extérieures qui s’exercent sur la voiture : poids, réaction du support et force motrice $*\vec{F}*$. Le poids et la réaction du support se compensent car la voiture a un mouvement horizontal. Donc $* \Sigma \vec{F}_{ext} = \vec{F}*$.
5. La 2e loi de Newton dit ici que $* \vec{F} = m\vec{a} *$. Donc $*\vec{F}*$ et $*\vec{a}*$ ont même sens et même direction. Donc $* F = ma *$ = 1420×3,86 ≃ 5,5 kN.