C4. Cinétique chimique
Une réaction chimique ne se fait pas de manière instantané. Il faut le temps que les réactifs se rencontrent, puis qu’ils réagissent. Une branche de la chimie étudie cette aspect des réactions chimiques : c’est la cinétique chimique.
Réaction rapide, réaction lente
- Justifier le choix d’un capteur de suivi temporel de l’évolution d’un système.
- Identifier, à partir de données expérimentales, des facteurs cinétiques.
- Citer les propriétés d’un catalyseur et identifier un catalyseur à partir de données expérimentales.
- Interpréter l’influence des concentrations et de la température sur la vitesse d’un acte élémentaire, en termes de fréquence et d’efficacité des chocs entre entités.
TP Suivi d’une réaction chimique
- Mettre en œuvre une méthode physique pour suivre l’évolution d’une concentration et déterminer la vitesse volumique de formation d’un produit ou de disparition d’un réactif.
- Mettre en évidence des facteurs cinétiques et l’effet d’un catalyseur.
Objectif : étudier la cinétique de la réaction entre les ions iodures $*\ce{I-}*$ et les ions peroxodisulfate $*\ce{S4O8^2-}*$ en faisant varier différents paramètres
Matériel disponible
- Solution S1 d’iodure de potassium ($*\ce{K+ + I-}*$) à $*c_1*$ = 0,50 mol·L-1
- Solution S2 de peroxodisulfate de sodium ($*\ce{2Na+ + S2O8^2-}*$) à $*c_2*$ = 20 mmol·L-1
- Colorimètre et filtres
- Verrerie usuelle
À propos de cette réaction
Les ions peroxodisulfate $*\ce{S2O8^2-}*$ sont des oxydants appartenant au couple $*\ce{S2O8^2-}/\ce{SO4^2-}*$. Ils sont capables d’oxyder les ions iodure en diiode. Cette réaction est lente et totale, c’est-à-dire qu’elle se poursuit jusqu’à épuisement d’un des réactifs (nous y reviendrons dans le chapitre C5).
1.a. Écrire l’équation-bilan de la réaction.
1.b. Sachant que le diiode est la seule espèce chimique colorée (le diiode est jaune-brun en solution aqueuse) et que la réaction se déroule en solution aqueuse, décrire ce que l’on observera au cours de la réaction.
1.c. En déduire quel filtre choisir pour le colorimètre pour pouvoir suivre l’évolution de la concentration de $*\ce{I2}*$ formée
Préparer le colorimètre pour des mesures d’absorbance due au diiode (choix du filtre adéquat + faire un blanc)
Cinétique de la réaction de référence
- Dans un petit bécher, verser 10,0 mL de S2 prélevés avec une pipette jaugée.
- Verser 10 mL d’eau disillée mesurés à l’éprouvette graduée.
- Verser 10 mL de S1 mesurés à l’éprouvette graduée, mélanger avec une baguette de verre et déclencher le chronomètre en même temps.
- Verser ce mélange dans une cuve et placer cette cuve dans le colorimètre.
- Noter l’absorbance du mélange toute les 30 secondes environ, jusqu’à ce que celle-ci n’évolue presque plus (25 minutes maxi). L’idéal est de noter les valeurs directement dans un tableur.
2.a. Calculer la concentration finale du mélange en $*\ce{I2}*$ après avoir dressé le tableau d’avancement de la réaction.
2.b. En déduire la constante de proportionnalité $*k*$ de la loi de Beer-Lamber $*A = k·c*$ dans ces conditions. Préciser son unité.
2.c. À l’aide d’un tableur, tracer le graphique $*[\ce{I2}] = f(t)*$.
Cinétique de la réaction à une température supérieur
- Refaite la même expérience que précédemment, mais en remplaçant les 10 mL d’eau distillée par 10 mL d’eau distillée bien chaude.
3. Tracer sur le même graphique la courbe $*[\ce{I2}] = f(t)*$ pour cette nouvelle expérience. Qu’observe-t-on ?
Cinétique de la réaction à une concentration de réactif supérieure
- Même expérience que la première, mais en utilisant 20 mL de S1 au lieu de 10 mL et pas d’eau distillée.
4.a. Calculer la concentration finale du mélange en $*\ce{I2}*$.
4.b. Tracer sur le même graphique la courbe $*[\ce{I2}] = f(t)*$ pour cette nouvelle expérience. Qu’observe-t-on ?
Éléments de réponses
Dans les trois expériences, le réactif limitant est l’ion peroxodisulfate. Un tableau d’avancement montre que le $*x_\max*$ est le même pour les trois expériences. Et comme le volume du mélange réactionnel est le même (30 mL), la concentration en diiode en fin de réaction sera la même pour les trois expériences.
Ce constat permet de déduire la relation entre l’absorbance $*A*$ mesurée et la concentration en diiode $*\ce{[I2]}*$ au cours du temps.
Le graphique ci-dessous montre les concentrations en diiode au cours du temps pour les trois expériences, dans l’ordre bleu – orange – gris.
On constate que la réaction est plus rapide quand la température est plus élevée (comparaison bleu – orange).
On constate que la réaction est plus rapide quand la concentration d’un réactif est plus élevée (comparaison bleu – gris)
Un système chimique, s’il n’est pas stable, évolue de son état initial vers son état d’équilibre.
Cette évolution prend un certain temps, appelé durée de réaction.
Une réaction est dite rapide si, à l’œil nu, elle paraît terminée dès que les réactifs entrent en contact (réaction acido-basique, par exemple). Sinon, elle est dite lente (combustion d’une feuille de papier, oxydation du fer par le dioxygène de l’air, etc.).
Facteurs cinétiques
Certains paramètres expérimentaux modifient la vitesse de réaction. On les appelles des « facteurs cinétiques ».
Au niveau microscopique, une réaction entre deux entités chimiques se fait lorsqu’elles :
- se rencontrent (il faut donc qu’il y ait un choc entre elles) ;
- se heurtent avec la bonne orientation et suffisament d’énergie pour qu’elles puissent interagir et se transformer (on parle de choc « efficace »)
Les facteurs cinétiques ont une influence sur le nombre de chocs et sur la probabilité qu’un choc donné soit « efficace », c’est-à-dire donne lieu à une transformation chimique
Température
Plus la température est élevée, plus le mouvement des entités chimiques est rapide, et donc plus les chocs entre elles sont nombreux et violents. Ceci rend la réaction plus rapide.
Concentration des réactifs
Dans une solution, plus les réactifs sont concentrés, plus la probabilité qu’ils se rencontrent est grande et donc plus il y a de chocs entre eux. Ceci rend également la réaction plus rapide.
Catalyseur
Un catalyseur est une espèce chimique qui augmente la vitesse d’une réaction donnée mais dont la quantité à l’état initial est égale à la quantité à l’état final. Il n’apparaît pas dans l’équation-bilan.
• Un catalyseur ne fournit pas d’énergie. Il ne permet donc pas de réaliser une réaction non spontanée, c’est-à-dire qui nécessite un apport d’énergie pour se réaliser.
• Un catalyseur peut être sélectif, c’est-à-dire favoriser une réaction plutôt qu’une autre à partir du ou des mêmes réactifs.
Ainsi, à partir du même réactif mais en choisissant un catalyseur différent, on peut orienter la réaction vers un produit plutôt qu’un autre.
• Dans le cas d’une réaction limitée (ou non totale – souvenez-vous on en a un peu parlé l’année dernière au chapitre C3*), un catalyseur permet d’atteindre l’équilibre plus rapidement (modification de la cinétique de la réaction), mais ne modifie pas l’état d’équilibre du système chimique (c’est-à-dire son avancement final).

Vitesse de réaction
- À partir de données expérimentales, déterminer une vitesse volumique de disparition d’un réactif, une vitesse volumique d’apparition d’un produit ou un temps de demi-réaction.
Le paragraphe précédent était purement qualitatif, c’est-à-dire qu’on a seulement parlé de réactions plus ou moins rapides. Comment quantifier une vitesse de réaction ? C’est-à-dire l’évaluer par une valeur chiffrée ?
Oui et non ! 😊 Imaginons qu’on étudie la vitesse d’une réaction en solution aqueuse. Prenons celle que nous avons étudiée en TP pour fixer les idées : $µ\ce{S2O8^2- + 2 I^- \rightarrow 2 SO4^2- + I2}µ$
Un groupe d’élèves (groupe A) trouve que, à un instant $*t_0*$, la vitesse de formation du diiode $*v_{I_2}(t_0)*$ égale à 5 µmol·s-1. Ce groupe travaille avec un volume de solution $*V_A*$ = 100 mL.
Un autre groupe d’élèves (groupe B), qui travaillent avec un volume de la même solution $*V_B*$ = 200 mL, trouve $*v_{I_2}(t_0)*$ égale à 8 µmol·s-1.
Quel groupe a une vitesse de réaction la plus élevée ?
Dans l’absolu oui, mais le groupe B travaille avec un volume deux fois plus grand. Donc à volume égal, la réaction est en fait plus lente chez le groupe B que chez le groupe A. La coloration de la solution chez le groupe B (due à l’apparition de $*\ce{I2}*$) sera plus lente.
En fait, il est plus pertinent de déterminer une vitesse volumique de réaction, en mol·L-1·s-1, c’est-à-dire la vitesse de réaction pour un volume donné.
Vitesse volumique
La vitesse volumique d’apparition ou de disparition d’une espèce chimique, c’est la variation de sa concentration molaire au cours du temps. Si cette espèce chimique est un réactif, cette variation sera négative (puisqu’elle réagit, sa concentration diminue au cours du temps). Donc en prend la valeur absolue de cette variation en précisant s’il s’agit d’une vitesse de disparition ou d’apparition dont on parle.
Écrit plus simplement, ça donne :
| $µ v_X(t) = \left| \frac {\mathrm{d}\ce{[X]}}{\mathrm{d}t} \right| µ$ | $*v_X(t)*$ : vitesse volumique d’apparition / disparition de l’espèce X $*\ce{[X]}*$ : concentration molaire de l’espèce X |
Cette grandeur se détermine la plupart du temps de manière expérimentale à partir d’un graphique
Temps de demi-réaction
Une définition à savoir par cœur :

Cette grandeur est souvent utilisée pour quantifier une vitesse de réaction sur l’ensemble de son déroulement, afin de pouvoir la comparer à une autre vitesse.
✋ $*t_{1/2}*$ n’est pas moitié de la durée de réaction !!!
Évolution d’une qdm au cours du temps
L’avancement de réaction n’est pas une grandeur que l’on peut déterminer directement par l’expérience. Seules les quantités de matière de produits et/ou de réactifs peuvent être déterminées par un suivi approprié (spectrophotométrie, conductimétrie…).
Les quantités de matières de réactifs et de produits sont, évidemment, liées à l’avancement de réaction.
✋ Il faut savoir faire un tableau d’avancement pour pouvoir trouver cette relation !
Vitesse de réaction
On a mesuré la concentration en $*\ce{I2}*$ d’une solution où se déroule la réaction $µ\ce{S2O8^2- + 2 I^- \rightarrow 2 SO4^2- + I2}µ$
On obtient les mesures suivantes :
| $*t*$ (min) | $*\ce{[I2]}*$ (mmol·L-1) | $*t*$ (min) | $*\ce{[I2]}*$ (mmol·L-1) |
|---|---|---|---|
| 0 | 0 | 11 | 4,7 |
| 1 | 1,13 | 12 | 4,73 |
| 2 | 1,98 | 13 | 4,82 |
| 3 | 2,66 | 14 | 4,86 |
| 4 | 3,13 | 15 | 4,85 |
| 5 | 3,58 | 16 | 4,90 |
| 6 | 3,86 | 17 | 4,95 |
| 7 | 4,13 | 18 | 4,98 |
| 8 | 4,33 | 19 | 4,94 |
| 9 | 4,51 | 20 | 4,94 |
| 10 | 4,62 | 21 | 4,96 |
À l’aide d’un tableur, déterminer :
1. le temps de demi-réaction ;
2. la vitesse initiale d’apparition de $*\ce{I2}*$
3. la vitesse d’apparition de $*\ce{I2}*$ à $*t*$ = 5 min
Correction

1. Temps de demi-réaction : environ 2,8 min (lecture graphique – construction en vert)
2. On trace la tangente à $*t*$ = 0 puis on détermine son coefficient directeur précisément (entre l’origine et le point A) : $*v*$ = 1,2 mmol/L/min.
3. On trace la tangente à $*t*$ = 5 min puis on détermine son coefficient directeur (entre les points B et C) : $*v*$ = 0,36 mmol/L/min.
Qdm et temps de demi-réaction
L’équation-bilan de la réaction d’oxydation de l’éthanol par l’ion permanganate en milieu aqueux s’écrit :
$* \ce{4 MnO4– + 12 H+ + 5 CH3CH2OH}*$ $*\ce{\rightarrow 4 Mn^2+ + 5 CH3CO2H + 11 H2O}*$
On fait réagir $*n_{1i}*$ = 50 mmol d’ions permanganate avec $*n_{2i}*$ = 70 mmol d’éthanol. Les ions $*\ce{H+}*$ sont en large excès. La quantité initiale $*n_{3i}*$ d’ions manganèse II et $*n_{4i}*$ d’acide éthanoïque est nulle. La réaction est totale.
1. Calculer l’avancement final de la réaction.
2. Donner la relation entre les différentes quantités de matière $*n_1*$, $*n_2*$, $*n_3*$ et $*n_4*$ et l’avancement de réaction.
3. Donner la valeur de ces quantités de matière en fin de réaction et pour $*t_{1/2}*$.
Correction
Tout peut se faire dans un tableau d’avancement. $*x_f*$ = 12,5 mmol.
| $*x*$ (mmol) | $*\ce{\quad 4 MnO4– + \; 12 H^+ \; + 5 C2H6O \rightarrow 4 Mn^2+ + 5 C2H4O2 \; + 11 H2O}*$ | |||||
| $*x*$ | $*50-4x*$ | Excès | $*70-5x*$ | $*4x*$ | $*5x*$ | Solvant |
| $*6,25*$ | $*25*$ | $*38,75*$ | $*25*$ | $*31,25*$ | ||
| $*12,5*$ | $*0*$ | $*7,5*$ | $*50*$ | $*62,5*$ | ||
La ligne 2, pour un $*x*$ quelconque, correspond à la question 2. Les lignes 3 et 4 correspondent à la question 3.
Cinétique et facteurs cinétiques
Soit une réaction chimique dont l’équation est de la forme : $µ \ce{A + 2B \rightarrow C + H2O} µ$
Cette réaction se fait en solution dans l’eau. À l’instant initial, $*n_{\mathrm{A}0}*$ = $*n_{\mathrm{B}0}*$ = 1,0 mol. Le milieu est maintenu à une température constante de 25 °C. La mesure de la quantité de matière de $*\ce{A}*$ au cours du temps a permis de tracer la courbe ci-dessous :

1. Compléter numériquement le tableau d’avancement de cette réaction totale.
| $*x*$ (mol) | $*\ce{\qquad A \quad + \quad 2B \quad \rightarrow \quad C \quad + \quad H2O \quad}*$ | |||
|---|---|---|---|---|
| 0 | Solvant | |||
| $*x*$ | ||||
| $*x_f = \quad*$ | ||||
2. Donner la définition du temps de demi-réaction $*t_{1/2}*$. Quelle est sa valeur ici ? (Faites apparaître la construction graphique).
3. Tracer l’allure de la courbe si la réaction était réalisée à une température supérieure à 25°C.
Correction
1. Tableau d’avancement
| $*x*$ (mol) | $*\ce{\qquad A \quad + \quad 2B \quad \rightarrow \quad C \quad + \quad H2O \quad}*$ | |||
|---|---|---|---|---|
| 0 | 1 | 1 | 0 | Solvant |
| $*x*$ | $*1-x*$ | $*1-2x*$ | $*x*$ | |
| $*x_f = 0,5*$ | $*0,5*$ | $*0*$ | $*0,5*$ | |
2. Temps au bout duquel $*x = \frac {x_{\max}}2*$. $*t_{1/2} \simeq*$ 1 min (construction graphique en rouge).
3. L’avancement final est le même, mais il est atteint plus rapidement (sur le graphique en vert).

Loi de vitesse d’ordre 1
- Identifier, à partir de données expérimentales, si l’évolution d’une concentration suit ou non une loi de vitesse d’ordre 1.
La loi de vitesse d’une réaction, c’est la relation qui existe entre la vitesse de réaction et tous les facteurs qui ont une influence sur celle-ci. Dans le cas général, la loi de vitesse ne peut pas être déduite directement de l’équation bilan de la réaction, elle doit être établie expérimentalement à partir de séries d’expériences.
Pour beaucoup de réactions faisant intervenir deux réactifs A et B, la loi de vitesse peut s’écrire $*v = k·\ce{[A]}^m·\ce{[B]}^n*$. $*n*$ et $*m*$ sont appelées les ordres partiels de la réaction (ils ne sont pas nécessairement égaux aux coefficients stœchiométriques, ils ne sont même pas nécessairement entiers ni positifs). $*k*$ est une constante qui dépend, entre autres choses, de la température.
L’ordre de la réaction est la somme $*n+m*$.
On n’étudiera ensemble que des réactions d’ordre 1 qui n’implique qu’un seul réactif (typiquement une réaction de décomposition comme celle du peroxyde d’hydrogène : $*\ce{H2O2 \rightarrow H2O + 1/2 O2}*$)
Pour une telle réaction, donc, on a $*v_{\ce{X}} = k\ce{[X]}*$. Ou encore, $* - \cfrac {\mathrm{d}[X]}{\mathrm{d}t} = k\ce{[X]}*$.
Oh ! Une équation différentielle ! 😄
On a supposé qu’on parlait, dans ce cas, de la vitesse de disparition d’un réactif. Donc $* \frac {\mathrm{d}[X]}{\mathrm{d}t} *$ est négatif dans ce cas. Du coup, à cause de la valeur absolue dans $* v_X(t) = \left| \frac {\mathrm{d}[X]}{\mathrm{d}t} \right| *$, on doit rajouter ce signe « – » pour se débarrasser des valeurs absolues.
Vous savez résoudre ce genre d’équa diff. La solution, c’est $*\ce{[X]}(t) = \ce{[X]_0}·e^{-kt} *$
Une conséquence intéressante, c’est que si on veut vérifier qu’une vitesse de réaction est d’ordre 1 par rapport au réactif $*\ce{X}*$, il suffit de tracer $*\ln \ce{[X]}*$ en fonction du temps. Si on obtient une droite (forcément décroissante), alors on a la preuve que la vitesse de réaction est d’ordre 1 par rapport à $*\ce{X}*$.
Preuve : si $* \ce{[X]} = \ce{[X]_0}·e^{-kt} *$, alors $*\ln \ce{[X]} = \ln \ce{[X]}_0 - kt*$

Vous devez savoir écrire un programme Python qui permet, à partir de données expérimentales, de tracer l’évolution temporelle d’une concentration, d’une vitesse volumique d’apparition ou de disparition et de tester une relation donnée entre la vitesse volumique de disparition et la concentration d’un réactif.
C’est un peu stupide de faire ça en Python sachant qu’un tableur permet de le faire beaucoup plus vite et plus simplement, mais bon, puisqu’on vous le demande… allons-y 😊
TP Loi de vitesse d’ordre 1
- Capacité numérique : à l’aide d’un langage de programmation et à partir de données expérimentales, tracer l’évolution temporelle d’une concentration, d’une vitesse volumique d’apparition ou de disparition et tester une relation donnée entre la vitesse volumique de disparition et la concentration d’un réactif.
Objectif : tester s’il y a une relation de proportionnalité entre la vitesse de disparition d’un réactif et sa concentration. En conclure quant à l’ordre de la loi de vitesse de la réaction.
Concentration et vitesse de disparition en fonction du temps
Vous trouverez dans ce fichier des données concernant la concentration $*c*$ d’un réactif $*\ce{X}*$ (en mmol/L) en fonction du temps (en secondes) déterminées expérimentalement. Elles ont déjà été mise en forme de liste Python pour une utilisation plus facile sur repl.it. Les données $*t_{exp}*$ et $*c_{exp}*$ sont celles que nous avons obtenues lors du TP précédents (1ère expérience).
- Dans cette première partie, vous allez écrire un programme qui affiche $*c*$ et $*v_{\ce{X}}*$ en fonction du temps.
Vous devez trouver un moyen de calculer une valeur approchée de $*v_{\ce{X}}*$ sans rien supposer de la loi de vitesse. On ne peut pas supposer à l’avance qu’elle est d’ordre 1.
Remarque : la valeur de la vitesse de réaction est très faible devant la valeur de la concentration. Si vous voulez que votre graphique soit lisible (et oui ! vous le voulez ! 😊) il faut utiliser un graphique avec deux axes des ordonnées…
t_exp = [0.0, 17.0, 47.0, 77.0, 107.0, 137.0, 167.0, 197.0, 227.0, 257.0, 287.0, 317.0, 347.0, 377.0, 407.0, 437.0, 467.0, 497.0, 527.0, 557.0, 587.0, 617.0, 647.0, 677.0, 707.0, 737.0, 767.0, 797.0, 827.0, 857.0, 887.0, 917.0, 947.0, 977.0, 1007.0, 1037.0, 1067.0, 1097.0, 1127.0, 1157.0, 1187.0, 1217.0, 1247.0, 1277.0, 1307.0, 1337.0, 1367.0, 1397.0, 1427.0, 1457.0, 1487.0, 1517.0]
c_exp = [0.0, 0.333, 0.805, 1.238, 1.662, 2.033, 2.386, 2.705, 2.981, 3.248, 3.476, 3.695, 3.895, 4.067, 4.233, 4.386, 4.524, 4.652, 4.762, 4.871, 4.971, 5.057, 5.143, 5.224, 5.295, 5.362, 5.424, 5.476, 5.524, 5.614, 5.629, 5.667, 5.714, 5.762, 5.795, 5.819, 5.862, 5.89, 5.91, 5.943, 5.967, 5.99, 6.01, 6.038, 6.062, 6.071, 6.09, 6.11, 6.124, 6.148, 6.162, 6.171]
v_exp = []
for i in range (len(c_exp)-1) :
v_exp.append((c_exp[i+1]-c_exp[i])/(t_exp[i+1]-t_exp[i]))
import matplotlib.pyplot as plt
fig, axe1 = plt.subplots()
axe1.set_xlabel('t(s)')
axe1.set_ylabel('c (mmol/L', color='b')
# axe1.set_ylim(min, max)
for valeur in axe1.get_yticklabels() :
valeur.set_color('b') # couleur graduation gauche
axe2 = axe1.twinx()
axe2.set_ylabel('v(I2) (mmol/L/s)', color='r')
# axe2.set_ylim(min, max)
for valeur in axe2.get_yticklabels():
valeur.set_color('r') # couleur graduation droite
axe1.plot(t_exp, c_exp, 'bo', ms=5)
axe2.plot(t_exp[0:-1], v_exp, 'ro', ms=5)
# si on veut ajouter y3 connecté à l’axe 2
# axe2.plot(x, y3, 'go', ms=5)
plt.show()
Vitesse de disparition en fonction de la concentration
- Modifier votre code pour qu’il affiche $*v_{\ce{X}} = f(c)*$. Il vaut mieux ne rien effacer du code que vous avez déjà. Passez les lignes inutiles en commentaires pour les désactiver.
Question : que constatez-vous ? Est-ce que cela laisse présager quelque chose sur l’ordre de la vitesse de réaction ?
Modélisation de la vitesse de réaction en fonction du temps
Dans cette section, on va voir quelque chose de nouveau : la modélisation par une fonction affine d’une série de valeur. Vous savez le faire sur un tableur (Ajouter une courbe de tendance…), mais pas sur Python. C’est très simple, et le modèle est plus précis que sur Excel. Allez voir dans la section Python.
- Ajouter une droite de régression à la courbe $*v_{\ce{X}} = f(c)*$.
Question : que peut-on conclure ?
Autre réaction
La série de mesure $*c_2*$ correspond-elle à une cinétique de réaction d’ordre 1 ?
Éléments de réponse
Le code ci-dessous contient plus que ce qu’il faut faire, car il affiche simultanément les deux graphiques demandés au cours du TP.
import matplotlib.pyplot as plt
import scipy.stats as sst
# les données
t1 = [0.0, 50.0, 100.0, 150.0, 200.0, 250.0, 300.0, 350.0, 400.0, 450.0, 500.0, 550.0, 600.0, 650.0, 700.0, 750.0, 800.0, 850.0, 900.0, 950.0, 1000.0, 1050.0, 1100.0, 1150.0, 1200.0, 1250.0, 1300.0, 1350.0, 1400.0]
c1 = [15.01, 13.28, 11.57, 10.32, 9.12, 8.06, 7.04, 6.29, 5.56, 4.84, 4.34, 3.78, 3.37, 2.94, 2.61, 2.29, 2.03, 1.81, 1.58, 1.4, 1.23, 1.08, 0.96, 0.84, 0.74, 0.66, 0.59, 0.52, 0.45]
c2 = [15.0, 7.5, 5.0, 3.75, 3.0, 2.5, 2.14, 1.88, 1.67, 1.5, 1.36, 1.25, 1.15, 1.07, 1.0, 0.94, 0.88, 0.83, 0.79, 0.75, 0.71, 0.68, 0.65, 0.63, 0.6, 0.58, 0.56, 0.54, 0.52]
t_exp = [0.0, 17.0, 47.0, 77.0, 107.0, 137.0, 167.0, 197.0, 227.0, 257.0, 287.0, 317.0, 347.0, 377.0, 407.0, 437.0, 467.0, 497.0, 527.0, 557.0, 587.0, 617.0, 647.0, 677.0, 707.0, 737.0, 767.0, 797.0, 827.0, 857.0, 887.0, 917.0, 947.0, 977.0, 1007.0, 1037.0, 1067.0, 1097.0, 1127.0, 1157.0, 1187.0, 1217.0, 1247.0, 1277.0, 1307.0, 1337.0, 1367.0, 1397.0, 1427.0, 1457.0, 1487.0, 1517.0]
c_exp = [0.0, 0.333, 0.805, 1.238, 1.662, 2.033, 2.386, 2.705, 2.981, 3.248, 3.476, 3.695, 3.895, 4.067, 4.233, 4.386, 4.524, 4.652, 4.762, 4.871, 4.971, 5.057, 5.143, 5.224, 5.295, 5.362, 5.424, 5.476, 5.524, 5.614, 5.629, 5.667, 5.714, 5.762, 5.795, 5.819, 5.862, 5.89, 5.91, 5.943, 5.967, 5.99, 6.01, 6.038, 6.062, 6.071, 6.09, 6.11, 6.124, 6.148, 6.162, 6.171]
# choix de la série de données
t = t_exp
c = c_exp
# calcul de la vitesse de réaction
v=[]
for i in range(len(c)-1):
v.append(-(c[i+1]-c[i])/(t[i+1]-t[i]))
# on supprime les données pour lesquelles la vitesse ne peut pas être calculée
del t[-1]
del c[-1]
# la régression linéaire
a,b,r,p,err = sst.linregress(c,v)
text = f"y = {a:.2e}·x + {b:.2e} \n R² = {r**2:.4f}"
vm=[a*x+b for x in c]
# les graphiques
fig, (axe1, axe2) = plt.subplots(2,1)
axe1.set_xlabel('temps (s)')
axe1.set_ylabel('[X] (mmol/L)', color='b')
axe1.plot(t,c,'bx', ms = 5)
axe1b = axe1.twinx()
axe1b.set_ylabel('$v_\mathrm{X}$ (mmol/L/s)', color='r')
axe1b.plot(t, v, 'rx', ms = 5)
axe2.set_xlabel('concentration (mmol·L$^{-1}$)')
axe2.set_ylabel('vitesse disparition\n(mmol/L/s)')
axe2.plot(c, v, 'bx', ms = 5)
axe2.plot(c, vm, 'r')
axe2.text (0.05,0.75, text, transform=axe2.transAxes)
fig.tight_layout(pad=2.0)
plt.show()
Modélisation microscopique
- À partir d’un mécanisme réactionnel fourni, identifier un intermédiaire réactionnel, un catalyseur et établir l’équation de la réaction qu’il modélise au niveau microscopique.
- Représenter les flèches courbes d’un acte élémentaire, en justifiant leur sens.
Cette partie n’est pas au programme des épreuves écrites de mars 2022.
Mécanisme réactionnel
Une transformation chimique nécessite une rencontre entre les réactifs au niveau microscopique. Beaucoup de réactions se déroulent en plusieurs étapes, c’est-à-dire que pour passer des réactifs aux produits finaux, il y a plusieurs étapes intermédiaires. Chaque étape correspond à un choc entre deux entités chimiques, qui conduit à une modification de la répartition des électrons autour de ces entités.
Au cours de ces étapes, il se forment des entités chimiques dont la durée de vie est extrêmement brève et que l’on appelle des intermédiaires réactionnels.
Un mécanisme réactionnel est noté en matérialisant, par des flèches courbes les mouvements des électrons entre les réactifs.
La figure ci-dessus montre un mécanisme réactionnel simple, correspondant à l’équation-bilan de la réaction $µ\ce{Cl–C(CH3)3 + HO^- \rightarrow Cl^- + OH–C(CH3)3}µ$
Que nous indique-t-elle ? Eh bien que lorsque l’ion hydroxyde rencontre la molécule de 2-chloro-2-méthylpropane,
- un électron d’un des doublets non liant de l’oxygène est donné au carbone porteur du chlore, ce qui crée une liaison C–O
- le chlore récupère un électron de la liaison C–Cl. Ça le transforme en ion chlorure et il n’est plus lié au carbone.
Un mécanisme réactionnel est la suite des différentes étapes menant des réactifs aux produits (il peut y en avoir qu’une seule).
Chaque étape correspond à un choc entre deux entités, au cours du quel il y a des déplacement d’électrons.
Le mouvement de ces électrons est symbolisé par une flèche courbe, qui part de l’emplacement initial des électrons et qui va vers leur nouvel emplacement.
Bien sûr, on ne vous demande pas de deviner un mécanisme réactionnel, mais simplement de comprendre sa représentation. 😅
Influence d’un catalyseur
Un catalyseur modifie le mécanisme réactionnel d’une réaction. Il intervient dans une ou plusieurs étapes de celle-ci en les remplaçant par des étapes plus rapides.
Du coup, la réaction est plus rapide. Le catalyseur est nécessairement régénéré à la fin de la réaction, même s’il participe au mécanisme réactionnel.
La réaction d’estérification, par exemple, est une réaction qui a lieu entre un acide carboxylique et un alcool. Son équation-bilan est : $µ \ce{R^{1}–COOH + R^{2}–OH \leftrightarrows R^{1}–COO–R^2 + H2O} µ$
Celle-ci est catalysée par l’ion $*\ce{H+}*$. Son mécanisme réactionnel ci-dessous rend très bien compte de cela.
On voit que c’est le catalyseur qui permet d’obtenir facilement le premier intermédiaire réactionnel. À partir de là, les autres étapes de la réaction peuvent se dérouler. On voit également qu’un fin de réaction, l’ion $*\ce{H+}*$ impliqué en début de réaction est régénéré.
Mécanisme réactionnel
La synthèse du paracétamol se produit en trois étapes ci-dessous. Compléter chaque étape avec la ou les flèches courbes qui rendent compte de l’obtention de l’intermédiaire.
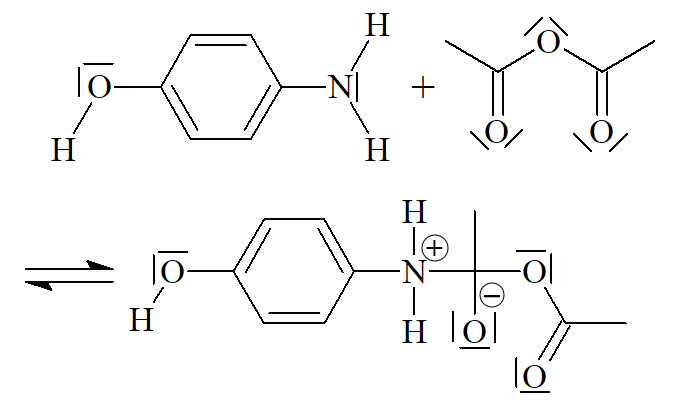
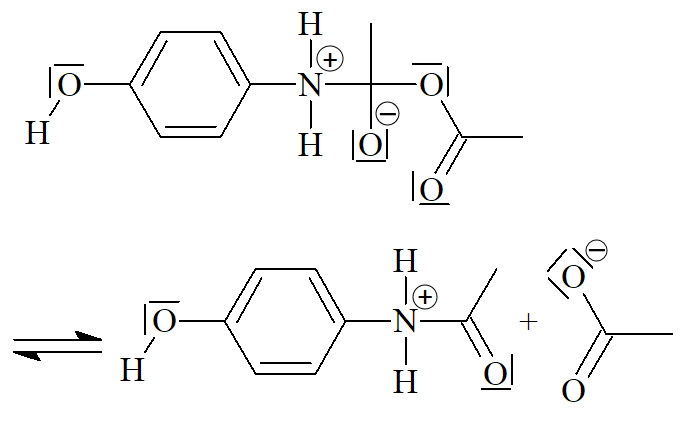
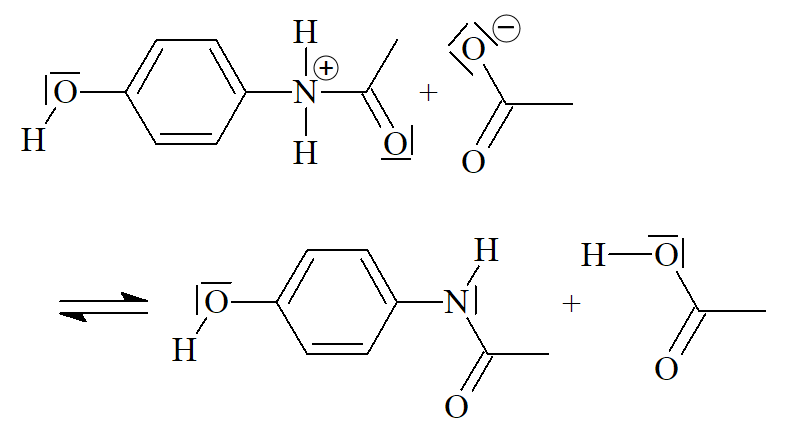
Correction
Révision & entraînement
Décomposition de H2O2
La décomposition du peroxyde d’hydrogène $*\ce{H2O2(aq)}*$ aboutit à la formation d’eau $*\ce{H2O(\ell)}*$ et de dioxygène $*\ce{O2(g)}*$.
On réalise le suivi de cette réaction avec une quantité de matière initiale de peroxyde d’hydrogène est égale à $*n_0(\ce{H2O2}*$) = 20,0 mol.

1. Écrire l’équation-bilan de cette réaction.
2. Calculer l’avancement maximum.
3. À l’aide du graphique, déterminer le temps de demi-réaction $*t_{1/2}*$.
4. Comment faire pour améliorer la conservation d’une solution concentrée de $*\ce{H2O2}*$.
5. Cette réaction est-elle d’ordre 1 ?
Correction
1. $*\ce{H2O2 \rightarrow H2O + 1/2 O2}*$
2. $*x_{\max}*$ = 20,0 mol
3. On a déjà vu plusieurs fois la construction. On trouve $*t_{1/2}*$ ≃ 1350 s.
4. Il faut la stocker au froid (et/ou la diluer, à condition qu’on n’ait pas besoin quelle soit concentrée pour une utilisation ultérieure.
5. Le raisonnement est le même que pour le TP Loi de vitesse d’ordre 1. Par une lecture graphique, on trouve $*n(\ce{O2})*$ pour différentes valeurs de $*t*$.
Puis on précise que la vitesse d’apparition de $*\ce{O2}*$ est proportionnelle à la vitesse de disparition de $*\ce{H2O2}*$.
On ne connaît pas le volume de la solution qui contient les 20 mol de $*\ce{H2O2}*$, mais peu importe, on sait que $*\ce{[H2O2]}*$ est proportionnel à $*n_{\ce{H2O2}}*$.
Ensuite, on calcule une approximation de la vitesse de réaction au temps $*t_i*$ en faisant $* v \simeq \cfrac {n_\ce{O2}(t_{i+1}) - n_\ce{O2}(t_{i-1})}{t_{i+1} - t_{i-1}}*$.
On obtient les résultats suivants :
| $*t*$ | $*n_{\ce{O2}}*$ | $*v*$ | $*n_{\ce{H2O2}}*$ |
|---|---|---|---|
| 0 | 0 | – | 20 |
| 1000 | 4 | 0,00635 | 12 |
| 2000 | 6,35 | 0,0039 | 7,3 |
| 3000 | 7,9 | 0,00235 | 4,2 |
| 4000 | 8,7 | 0,0013 | 2,6 |
| 5000 | 9,2 | 0,0008 | 1,6 |
| 6000 | 9,5 | 0,0006 | 1 |
| 7000 | 9,8 | 0,0004 | 0,4 |
| 8000 | 9,9 | – | 0,2 |
Lorsqu’on trace $*v*$ en fonction de $*n_{\ce{H2O2}}*$, on constate que les deux grandeurs sont proportionnelles. La réaction est donc bien d’ordre 1.

Iodation de la propanone
Soit la réaction totale d’équation-bilan : $µ \ce{CH3COCH3(aq) + I2(aq) \rightarrow CH3COCH2I(aq) + H^+(aq) + I^−(aq)} µ$
On effectue le suivi spectrophotométrique de cette réaction. Les mesures d’absorbance sont consignées dans le tableau ci-dessous. Les conditions initiales du mélange réactionnel sont telles que la propanone est introduite en large excès.
La seule espèce colorée est le diiode.
| $*t*$ (min) | Absorbance $*A*$ | $*t*$ (min) | Absorbance $*A*$ |
|---|---|---|---|
| 0 | 1,89 | 6 | 1,28 |
| 1 | 1,79 | 7 | 1,17 |
| 2 | 1,68 | 8 | 1,07 |
| 3 | 1,58 | 9 | 0,97 |
| 4 | 1,48 | 10 | 0,88 |
| 5 | 1,38 | 11 | 0,77 |
1. Exprimer la concentration en diiode $*\ce{[I2]}*$ en fonction de l’absorbance $*A*$ de la solution.
2. En déduire le temps de demi-réaction en le justifiant.
3. Est-ce une réaction d’ordre 1 par rapport au diiode ?
Correction
1. C’est la loi de Beer-Lambert : $*A=k·\ce{[I2]}*$
2. Il y a une relation de proportionnalité entre $*A*$ et $*\ce{[I2]}*$. La réaction est totale et $*\ce{I2}*$ = 0 à l’état final. Lorsque $*t=t_½*$, $*x*$ = $*\frac {x_\max}2*$ et donc la moitié du diiode a réagi et l’absorbance a diminué de moitié.

On trouve $*t_½*$ ≃ 9,25 minutes.
3. Pour une réaction d’ordre 1, la vitesse de disparition du réactif est proportionnelle à la concentration du réactif. Or ici, on voit que $*\ce{[I2]}*$ décroit linéairement. Donc la vitesse de disparition de $*\ce{I2}*$ est constante. Ce n’est donc pas une réaction d’ordre 1.
Fermentation malolactique
Cet exercice a été donné en devoir en 2020/2021.
Lors de la fermentation malolactique, l’acide malique présent dans le vin se transforme en acide lactique, avec production de $*\ce{CO2}*$ à l’état gazeux. Cette transformation est modélisée par l’équation-bilan :
Données
- masse molaire de l’acide malique : $*M_{mal}*$ = 134,0 g·mol-1
- masse molaire de l’acide lactique : $*M_{lac}*$ = 90,0 g·mol-1
Un vigneron suit la fermentation malolactique d’un vin contenu dans une cuve. La température ambiante est de 15 °C. La concentration massique initiale en acide malique dans le vin est de 3,0 g·L-1. La concentration massique en acide lactique au cours du temps est représentée sur le graphique ci-dessous.

1. La fermentation malolactique est-elle une transformation totale ? Justifier.
2.1. Donner la définition du temps de demi-réaction d’une transformation chimique.
2.2. En expliquant votre raisonnement, calculer le temps de demi-réaction de cette transformation.
3. Estimer graphiquement la vitesse volumique initiale d’apparition de l’acide lactique. Indiquez clairement l’unité de cette vitesse.
On souhaite savoir si l’évolution de la vitesse volumique de disparition de l’acide malique peut être modélisée par une loi d’ordre 1. Pour cela, on écrit un programme en Python qui permet de calculer les vitesses volumiques de disparition de l’acide malique aux différentes dates, puis de représenter l’évolution de cette vitesse en fonction de la concentration de l’acide malique.
Extrait du programme Python
# temps en jour et concentration acide malique en mmol/L
t = [0.0, 0.5, 1.0, 1.5, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0,
10.0, 12.0, 14.0, 16.0, 18.0, 20.0, 22.0]
c = [22.39, 19.05, 16.05, 13.5, 11.28, 7.94, 5.5, 3.72, 2.5,
1.72, 1.17, 0.5, 0.28, 0.17, 0.11, 0.05, 0.0, 0.0]
# calcul de la vitesse de réaction
v=[]
for i in range(len(c)-1):
v.append(-(c[i+1]-c[i])/(t[i+1]-t[i]))
Une partie du programme non reproduite ci-dessus permet de modéliser les résultats obtenus par une fonction affine.

4.1. Expliquez, en vous appuyant sur l’extrait de programme proposé, pourquoi le calcul des vitesses volumiques de disparition donne une valeur approchée.
4.2. Indiquer si la cinétique de la fermentation malolactique peut être modélisée par une loi d’ordre 1. Justifier.
5. Si la température ambiante était de 20 °C, quel impact cela aurait-il sur le premier graphique ? Justifier.
Correction
1. Concentration initiale de l’acide malique : 3,0 g·L-1 → 22,4 mmol·L-1
Concentration de l’acide lactique à l’état final : 2,0 g·L-1 → 22,2 mmol·L-1
La réaction est donc totale (on est à deux chiffres significatifs)
2.1. Temps au bout du quel l’avancement de réaction a atteint la moitié de sa valeur finale.
2.2. La concentration massique en acide lactique est proportionnelle à l’avancement de réaction, donc on trouve $*t_½*$ par construction graphique lorsque la concentration en acide lactique est de 1,0 g·L-1 : 2 jours
3. Il faut tracer la tangente à la courbe à $*t*$ = 0.

On trouve une pente de cette tangente égale à 2,2 g·L-1 ÷ 3,3 jours = 0,76 g·L-1·jour-1, soit 8,4 mmol·L-1·jour-1.
4.1. La valeur réelle instantanée de la vitesse de réaction est obtenue pour un $*\Delta t*$ qui tend vers 0. Ici, on a un $*\Delta t*$ qui varie (selon les mesures) entre 0,5 jours et 2 jours. On n’obtient donc qu’une valeur approchée de la vitesse.
4.2. On voit que la vitesse de réaction est proportionnelle à la concentration du réactif. C’est la définition d’une réaction d’ordre 1. Donc la réponse est oui.
5. La vitesse de réaction serait plus élevée. Le graphique aurait la même allure que celui qui est montré, mais il tendrait plus vite vers la concentration finale de 2,0 g·L-1.