P1. Cinématique
La cinématique est la description mathématique d’un mouvement, sans s’intéresser à ses causes (c’est-à-dire les forces et/ou l’inertie à l’origine de ce mouvement). Son objectif est de mettre sous forme d’équations la position d’un objet en mouvement, ainsi que sa vitesse et son accélération.
Nous avons déjà fait, en première, un peu de mécanique au chapitre P3. Je vais tâcher, dans ce cours, de tout reprendre à zéro. Ça ne fera pas de mal… 😊
Sachez également que, au lycée, nous ne ferons que ce que l’on appelle de la « mécanique du point ». C’est à dire que nous réduirons tous les objets étudiés à leur centre de gravité. On appelle ce modèle un « point matériel » (matériel parce qu’il s’agit d’un point qui possède néanmoins une masse : la masse du système qu’il représente.)
Oui, dans certains cas. Ça revient, entre autres, à ignorer l’éventuelle rotation de l’objet sur lui-même au cours du mouvement.
Préalables
Quelques définitions pour fixer les idées.
Système
Lorsqu’on étudie un mouvement, il faut clairement définir le système que l’on étudie.
Par exemple, on peut étudier le mouvement du système Terre-Lune autour du Soleil. Ce n’est pas le même que le mouvement du système Lune autour du Soleil.
Référentiel
Vous savez, depuis la sixième, qu’un mouvement est « relatif ». Le mouvement d’un système ne peut être étudié que par rapport à un autre objet, qu’on appelle un référentiel. Dans la vie courante, le référentiel que l’on choisit le plus souvent, parfois de manière inconsciente, c’est le référentiel terrestre, c’est-à-dire le sol.
- terrestre (le sol) ;
- géocentrique (centre de la Terre) ;
- héliocentrique (centre du Soleil) ;
Eh bien, c’est soit l’exercice qui vous l’indique, soit vous qui le choisissez. Dans ce cas, il est important que vous explicitiez bien quel référentiel vous avez choisi.
Repère
Mettre en équation le mouvement d’un système, c’est-à-dire le modéliser mathématiquement, c’est exprimer ses coordonnées de position en fonction du temps. Et qui dit coordonnées dit … repère.
Eh bien parce que l’Univers (du moins sa partie visible) possède 3 dimensions d’espace (et une de temps). Donc si vous voulez définir la position d’un point, il vous faut trois coordonnées, que l’on note généralement $*x*$, $*y*$ et $*z*$.
Mais, bonne nouvelle, on étudiera en terminale seulement des mouvements rectilignes et des mouvements plans. Dans une trajectoire rectiligne, le mouvement du système se fait selon une droite. Du coup, si vous choisissez bien votre repère, il n’y a qu’une seule coordonnée qui varie. On peut donc choisir un repère avec un seul axe (parce que sur les deux autres, les coordonnées du système sont constantes).
Et dans le cas d’une trajectoire plane, si vous choisissez bien votre repère, il n’y a que deux coordonnées qui varient, donc… je vous laisse deviner la suite. 😊
Référentiel et repère
On souhaite étudier la trajectoire d’un ballon lancé par un joueur de basket.
• Quel référentiel est-il pertinent de choisir ?
• Quel repère est-il pertinent de choisir ?
Pour répondre à cette dernière question vous devez indiquer l’orientation des axes du repère de manière à ce que le mouvement soit le plus simple possible à décrire.
Correction
Il faut choisir le référentiel terrestre (ça n’aurait aucun sens d’étudier le mouvement du ballon par rapport au joueur, car celui-ci peut être en mouvement pendant le déplacement du ballon.
Pour ce qui est du repère, on oriente son axe horizontal dans le sens du déplacement du ballon, de manière à ce que la partie « horizontale » du déplacement ne se fasse que selon cet axe. On évite ainsi d’avoir trois coordonnées pour repérer le ballon. Deux suffisent.
Vecteur position
Bon, alors pour la suite du chapitre, il va falloir être à l’aise avec les vecteurs. 😏
La position d’un point dans un repère, c’est tout simplement ses coordonnées. Jusque là, j’imagine que je ne vous apprends pas grand-chose.
Si on appelle M le point matériel dont on étudie le mouvement, la position du point M peut s’écrire : $* x(t)*$ ; $*y(t)*$ ; $*z(t)*$.
Non, pas dans ce cas ! $*x*$ est une fonction… du temps ! (enfin, sauf si l’objet est immobile. Mais là, ce n’est pas très intéressant à étudier… 😏) Comme on étudie des grandeurs qui varient au cours du temps, la variable sera le temps, noté $*t*$. Mais parfois, par commodité, on notera $*x(t)*$ simplement $*x*$, le fait que $*x*$ varie au cours du temps est sous-entendu. Pareil pour d’autres grandeurs ($*y*$, $*z*$, et d’autres que nous verrons plus tard).
Bonne question ! 😊 J’y arrive. On parle du vecteur position, en effet. Un vecteur, c’est quoi, au fond ? C’est simplement une collection de nombres (ou de fonctions dont la valeur est un nombre), que l’on appelle ses coordonnées. Et c’est bien ce qu’on a ici : un ensemble de trois nombres qui sont les coordonnées de $*\mathrm{M}*$.
Donc, le vecteur position, c’est le vecteur $* \overrightarrow{\mathrm{OM}} *$, $*\mathrm{O}*$ étant l’origine du repère, de coordonnées (0;0;0).
Vecteur vitesse
Bon, là il va falloir bien suivre, parce que ça se corse un peu ! 😊
Quand un objet est immobile dans un référentiel donné, c’est-à-dire quand son vecteur position $* \overrightarrow{\mathrm{OM}} *$ ne varie pas, que peut-on dire de sa vitesse ? Qu’elle est nulle, en effet.
En fait, le vecteur vitesse est lié à la variation du vecteur position.
Eh bien non ! Dans la vie courante, quand on parle de vitesse, on ne parle que de sa valeur. Mais ça ne suffit pas si on veut décrire un mouvement rigoureusement. Il faut indiquer également la direction dans laquelle se fait le mouvement. Et pour ça, on a besoin d’un vecteur.
Le vecteur vitesse, c’est en fait la dérivée du vecteur position : $µ \vec{v} ≝ { \mathrm{d}\overrightarrow{\mathrm{OM}} \over \mathrm{d}t } µ$
Mais non, mais non 😊. On va examiner cette formule pas à pas… Ça va aller. Il y a plusieurs choses importantes à comprendre :
- D’abord, commencez par remarquer le signe ≝. Cela signifie « égal par définition ». Cette relation est la définition même du vecteur $*\vec{v}*$. Elle est donc toujours vraie.
- Ensuite, remarquez la notation $*{ \mathrm{d}\overrightarrow{\mathrm{OM}} \over \mathrm{d}t }*$. Cette notation signifie « la dérivée par rapport au temps du vecteur $*\overrightarrow{\mathrm{OM}}*$ ». Voir la note ci-contre (ou ci-dessous si vous lisez ceci sur votre téléphone).
- Enfin, on voit qu’on peut dériver un vecteur. Ce point nécessite d’être un peu plus détaillé.
En physique, la notation $*f'(x)*$ devient : $µ f'(x) = { \mathrm{d}f(x) \over \mathrm{d}x } = { \mathrm{d}f \over \mathrm{d}x } µ$ Je reviendrai peut-être oralement sur la pertinence de cette notation.
Dérivée d’un vecteur
La dérivée d’un vecteur, ce n’est pas bien compliqué à comprendre si vous gardez bien en tête qu’un vecteur n’est qu’une simple collection de nombres ou, plus exactement, de grandeurs scalaires, qui sont ses coordonnées.
La dérivée $*\vec{w}*$ d’un vecteur $*\vec{m}*$ est elle-même un vecteur. Pour trouver les coordonnées de $*\vec{w}*$, rien de plus simple : il suffit de dériver les coordonnées de $*\vec{m}*$.
On peut donc réécrire la définition du vecteur vitesse comme ceci : $µ \vec{v} \begin{pmatrix} v_x(t) = { \mathrm{d}x(t) \over \mathrm{d}t } \\ v_y(t) = { \mathrm{d}y(t) \over \mathrm{d}t } \\ v_z(t) = { \mathrm{d}z(t) \over \mathrm{d}t } \end{pmatrix} µ$ On va, par commodité, utiliser une notation plus simple pour symboliser la dérivée d’une grandeur $*x*$ par rapport au temps. Cette notation est très utilisée dans le supérieur, mais vous ne la trouverez jamais au lycée. On va noter $*\dot{x}*$ la dérivée par rapport au temps de $*x*$. Vous avez le droit de vous servir de cette notation en devoir et au bac, à condition que vous précisiez sa signification, la première fois que vous l’utilisez.
Cela donne, pour le vecteur vitesse : $µ \vec{v} \begin{pmatrix} v_x(t) = \dot{x}(t) \\ v_y(t) = \dot{y}(t) \\ v_z(t) = \dot{z}(t) \end{pmatrix} µ$ Avouez que c’est plus simple. Mais attention, comme avec toutes les notations « raccourcies », il ne faut jamais oublier ce qu’il y a derrière.
Vecteur et norme
Quand on parle de la « valeur » de la vitesse (par exemple 50 km·h-1), on parle en fait de la norme de ce vecteur. Vous savez déjà comment calculer la norme d’un vecteur en fonction de ses coordonnées : $µ \Vert \vec{v} \Vert = \sqrt{v_x^2 + v_y^2 + v_z^2} µ$
1 m·s-1 = 3,6 km·h-1
En physique, on a pour habitude par commodité de noter $*v*$ plutôt que $* \Vert \vec{v} \Vert *$ la norme du vecteur $*\vec{v}*$.
Prenez donc bien garde à ne pas confondre ces différentes notations :
- $*\vec{v}*$ est le vecteur vitesse. Il ne s’agit en aucun cas d’un nombre, mais d’une collection de trois coordonnées.
- $*v*$ est la valeur de la vitesse, c’est la norme $*\Vert \vec{v} \Vert*$ de $*\vec{v}*$. Cette valeur est toujours positive.
- $*v_x*$, $*v_y*$ et $*v_z*$ sont les coordonnées du vecteur $*\vec{v}*$ sur les axes $*\mathrm{O}x*$, $*\mathrm{O}y*$ et $*\mathrm{O}z*$. Ce sont des nombres, qui peuvent être aussi bien positifs que négatifs ou nuls. Ça dépend de l’orientation du vecteur $*\vec{v}*$ par rapport à ces axes.
Allez ! Un petit exercice qui vous permettra de faire le point. Il est un peu abstrait, mais pour l’instant vous ne savez pas encore assez de choses pour étudier un cas concret plus intéressant. 😏
Vecteur vitesse
Imaginez un point $*M*$ qui glisse le long d’une droite à vitesse constante. On choisit un repère de manière à ce que cette droite coïncide avec l’axe $*\mathrm{O}x*$, les autres coordonnées $*y*$ et $*z*$ restent nulles tout au long du mouvement. Cet axe est gradué en mètres.
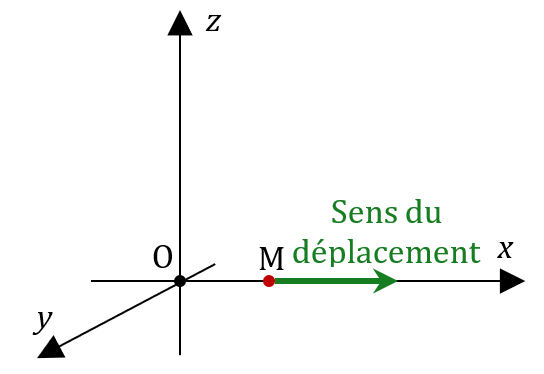
La coordonnée $*x(t)*$ du point M en fonction du temps s’écrit : $*x(t)=2t+2*$
1. Où se trouvait le point M à $*t = 0*$ ?
2. Quelles sont les coordonnées du vecteur $* \overrightarrow{\mathrm{OM}} *$ ?
3.a. Quelles sont les coordonnées du vecteur vitesse $*\vec{v}*$ ?
3.b. Quelle est la valeur de la vitesse $*v*$ ?
On change un peu la situation : l’objet est initialement au même endroit, il se déplace à la même vitesse mais cette fois dans le sens des $*x*$ décroissants.
4.a. Donner les coordonnées de son vecteur position.
4.b. Quelles sont les coordonnées de son vecteur vitesse $*\vec{v}*$ ?
4.c. Quelle est la valeur de sa vitesse $*v*$ ?
Correction
1. Le point M se trouvait en $*x(0) = 2*$.
2. $*x(t)=2t+2*$ ; $*y(t) = 0*$ et $*z(t) = 0*$
3.a. $*v_x = \dot{x} = 2*$ m·s-1 ; $*v_y = \dot{y} = 0*$ et $*v_z = \dot{z} = 0*$.
3.b. $* v = \sqrt{v_x^2 + v_y^2 + v_z^2} = 2*$ m·s-1.
4.a. Même endroit, donc $*x(0) = 2 *$. Par contre, vitesse opposée, donc $*x(t) = -2t +2*$
4.b. $*v_x(t)*$ = –2 m·s-1
4.c. $*v = \sqrt{v_x^2} =*$ 2 m·s-1
Vecteur accélération
- Définir le vecteur vitesse comme la dérivée du vecteur position par rapport au temps et le vecteur accélération comme la dérivée du vecteur vitesse par rapport au temps.
- Établir les coordonnées cartésiennes des vecteurs vitesse et accélération à partir des coordonnées du vecteur position et/ou du vecteur vitesse.
- Capacité mathématique : dériver une fonction, déterminer la primitive d’une fonction.
Là, il faut tout de suite clarifier un point important. Dans le langage commun, on dit qu’un objet « accélère » si sa vitesse augmente. En physique, ceci ne veut pas dire grand-chose, pour la bonne raison que la vitesse est une grandeur vectorielle. Qu’est-ce que ça veut dire « un vecteur qui augmente » ? Réponse : rien ! 😊
En physique, l’accélération est également un vecteur. Il ne suffit pas de dire de « combien » on accélère, mais également « vers où » on accélère.
Eh bien pas forcément. En physique, dès que le vecteur vitesse n’est pas constant, alors le vecteur accélération n’est pas nul. Pour faire simple (et pas très rigoureux 😊), dès qu’un objet tourne, « accélère » ou freine, son vecteur accélération n’est pas nul. Nous aurons l’occasion d’expliquer pourquoi lorsque nous verrons la deuxième loi de Newton.
La définition du vecteur accélération $*\vec{a}*$ est : $µ \vec{a} ≝ { \mathrm{d}\vec{v} \over \mathrm{d}t } µ$
Maintenant que vous savez dériver un vecteur, cette relation sera beaucoup plus claire pour vous. Un petit point sur les notations : $µ \vec{a} ≝ { \mathrm{d}\vec{v} \over \mathrm{d}t } ≝ { \mathrm{d}^2\overrightarrow{\mathrm{OM}} \over \mathrm{d}t^2 } µ$
On peut également écrire cela : $µ \vec{a} \begin{pmatrix} a_x(t) = \dot{v}_x(t) = \ddot{x}(t) \\ a_y(t) = \dot{v}_y(t) = \ddot{y}(t) \\ a_z(t) = \dot{v}_z(t) = \ddot{z}(t) \end{pmatrix} µ$
Notez les doubles points $*\ddot{x}*$, $*\ddot{y}*$ et $*\ddot{z}*$ pour indiquer que l’on parle de la dérivée seconde par rapport au temps. Notez aussi que l’on peut simplement sous-entendre que $*x*$, $*y*$ et $*z*$ sont des fonctions du temps, sans forcément écrire $*x(t)*$, $*y(t)*$ et $*z(t)*$. $µ \vec{a} \begin{pmatrix} a_x = \dot{v}_x = \ddot{x} \\ a_y = \dot{v}_y = \ddot{y} \\ a_z = \dot{v}_z = \ddot{z} \end{pmatrix} µ$
Attention : la simplicité de cette notation ne doit pas vous faire oublier tout ce qui se cache derrière !
Excellente question ! Merci de l’avoir posée ! 😎
Nous avons vu qu’il suffit de dériver le vecteur position $* \overrightarrow{\mathrm{OM}} *$ pour obtenir le vecteur vitesse $*\vec{v}*$. Pareil pour le vecteur accélération $*\vec{a}*$, il suffit de dériver le vecteur vitesse $*\vec{v}*$. Mais peut-on faire l’opération inverse ? Connaissant le vecteur accélération, peut-on en déduire le vecteur vitesse ?
Intégrer une fonction
Trève de suspense ! 😊 La réponse est… presque !
Faire l’opération inverse de « dériver », c’est intégrer. C’est, en générale, beaucoup plus compliqué d’intégrer une fonction que de la dériver, vous aurez largement l’occasion de le constater en math 😊. Mais en ce qui concerne la physique (du moins en terminale), j’ai une très bonne nouvelle : nous n’allons intégrer que des fonctions très très simples.
Pour intégrer une fonction $*f(t)*$, posez-vous la question : « quelle est la fonction $*F(t)*$ qui, lorsqu’on la dérive, me donne $*f(t)*$ ?
Tout ce que vous avez besoin de savoir, c’est :
- intégrer 0 : ça donne une constante $*a*$, parce que n’importe quelle constante, quand on la dérive, donne 0 ;
- intégrer une constante $*a*$ : ça donne une fonction affine $*at+b*$ ;
- intégrer une fonction affine $*at+b*$ : ça donne $* \frac12 at^2+bt+c*$.
Et voilà, c’est tout.
Rappelez-vous : $*x*$ n’est pas une variable mais une coordonnée de position.
Je reprends cette chaîne d’intégration, car il est capital que vous sachiez la retrouver :
Ça, je vous laisse y réflechir… 😉
Ah ! Voilà une question qui mérite qu’on s’y attarde un peu. Rappelez-vous un peu plus haut, lorsqu’on s’est posé la question « Est-ce qu’on peut connaître le vecteur vitesse $*\vec{v}*$ si on connaît le vecteur accélération $*\vec{a}*$ ? », je vous ai répondu « presque » 😊.
Prenons un exemple concret : un système, dans un référentiel donné, a un vecteur accélération $*\vec{a} = \vec{0}*$. Que peut-on dire de son vecteur vitesse ? Eh bien seulement qu’il est constant. En effet, si le vecteur accélération est nul, alors ses coordonnées sont : $µ \vec{a} \begin{pmatrix} a_x = 0 \\ a_y = 0 \\ a_z = 0 \end{pmatrix} µ$
Or d’après la définition même du vecteur accélération, que peut-on déduire de ça ? Eh bien que : $µ \begin{pmatrix} \dot{v}_x = 0 \\ \dot{v}_y = 0 \\ \dot{v}_z = 0 \end{pmatrix} µ$
Donc que peut-on dire de $*v_x*$, $*v_y*$ et $*v_z*$ si leur dérivée est nulle ? Tout simplement qu’il s’agit de constantes. Quelle valeur ont-elles ? Eh bien ça, on ne peut pas le dire sans avoir d’autres informations. Si on sait par exemple, que à $*t=0*$, $*v_x = 5*$, $*v_y = 0*$ et $*v_z = 0*$ (c’est-à-dire si on connaît la vitesse initiale, alors on pourra connaître à n’importe quel moment le vecteur vitesse $*\vec{v}*$ car on sait qu’il ne varie pas.
De manière plus générale, lorsqu’on intègre une fonction $*f(t)*$, il apparaît ce qu’on appelle une constante d’intégration dans l’expression de sa primitive $*F(t)*$ qu’on ne peut pas connaître, sauf si on connaît la valeur de $*F(t)*$ à un moment donné. Et en général, ce moment, c’est le moment correspondant au début du mouvement, à $*t=0*$.
Allez, sur cette seule notion d’intégration, je pense qu’il est temps de faire un excercice simple d’application, juste pour bien fixer les idées.
Intégrer une fonction
1.a. Soit la fonction $*f(t) = -6t + 2*$. Donner l’expression de sa primitive $*F(t)*$ pour laquelle $*F(0)=0*$.
1.b. Même question avec la fonction $*g(t) = 4*$ dont la primitive $*G(t)*$ vaut 5 pour $*t = 4*$.
2. Soit $*v(t)*$ la primitive d’une fonction $*a*$ constante. Soit $*x(t)*$ la primitive de la fonction $*v(t)*$. Donner l’expression de $*x(t)*$ sachant que $*v(0) = 0*$ et $*x(0) = 5*$.
Correction
1.a. Expression générale : $*F(t) = -3t^2 + 2t + c*$. Or $*F(0) = 0*$. Donc $*F(t) = -3t^2 + 2t*$ .
1.b. Expression générale : $*G(t) = 4t+c*$. Or $*G(4) = 4×4 + c = 5*$. Donc $*c = 5 - 16 = -11*$. Merci à Luka d’avoir remarqué l’erreur.
2. Expressions générales : $*v(t) = at+b*$ ; $*x(t) = \frac a2 t^2 + bt + c*$. Or $*v(0) = 0*$ donc $*b = 0*$. De plus, $*x(0) = 5*$, donc $*c=5*$.
Et maintenant un exercice un peu plus concret.
Mouvement rectiligne
Une voiture se déplace en ligne droite, à une vitesse constante de 30 m·s-1. Son passage en un point O constitue l’origine des dates (autrement dit, on considère que $*t = 0*$ lorsque la voiture passe par le point O). On souhaite étudier son mouvement dans le référentiel terrestre.
1. Choisissez un repère d’étude permettant le traitement mathématique le plus simple de son mouvement et donner les coordonnées des vecteurs accélération, vitesse et position de la voiture (que l’on assimilera à un point M).
2. Même question si on inverse l’orientation de tous les axes du repère.
Une moto initialement à l’arrêt s’apprête à courir le kilomètre départ arrêté. Elle part d’un point O et suit une trajectoire rectiligne de 1 km. La valeur de son accélération, supposée constante tout au long de son mouvement, est de 6,5 m·s-2.
3. Donner les coordonnées des vecteurs $*\vec{a}*$, $*\vec{v}*$, et $*\overrightarrow{\mathrm{OM}}*$ dans un repère de votre choix que vous expliciterez.
4. Déterminer :
a. Le temps au bout duquel la moto atteint 100 km/h ;
b. Le temps au bout duquel la moto franchit la ligne d’arrivée ;
c. La vitesse à laquelle elle franchit la ligne d’arrivée. Cette valeur vous paraît-elle réaliste ? D’où pourrait venir ce problème ?
Correction
1. Le plus simple est de choisir un repère dont l’axe $*\mathrm{O}x*$ est confondu avec la trajectoire de la voiture, dans le sens de son déplacement. Ça permet de n’avoir qu’une seule coordonnée (celle en $*x*$) à traiter pour tous les vecteurs, toutes les autres coordonnées sont nulles.
Toutes les valeurs sont en unités S.I
- $*v_x(t) = 30*$.
- $*a_x(t) = \dot{v}_x(t) = 0*$.
- $*x(t)*$ est la primitive de $*v_x (t)*$ : $*x(t) = 30t + x_0*$.
Or à $*t = 0*$, la voiture est à l’origine de l’axe donc $*x_0 = x(0) = 0*$
2. Si on inverse les axes du repère, la seule chose qui va changer est le signe des coordonnées de $*v_x(t)*$ et de $*x(t)*$.
3. On choisit un axe horizontal $*\mathrm{O}x*$ orienté dans le sens de déplacement de la moto. L’origine correspond au point de départ de la moto. On a donc : $*x_0 = 0*$ et $*\vec{v}_0 = \vec{0}*$ donc $*v_{0x} = 0*$.
Coordonnées des vecteurs : $*a_x=6,5*$ ; $*v_x=6,5t*$ ; $*x=3,25t^2*$
4.a. On veut savoir pour quelle valeur de $*t*$, $*v*$ = 100 km/h = 27,8 m·s-1.
Or $*v = \sqrt{v_x^2} = 6,5t*$.
On doit donc résoudre : $*6,5t = 27,8*$ soit $*t = 4,27*$ s
4.b. On cherche $*t*$ pour $*x*$ = 1000 m. On sait que $*x = 3,25t^2*$. Donc $*t=\sqrt{(1000/3,25)}=17,5*$ s.
4.c. On cherche $*v*$ pour $*t*$ = 17,5 s. Donc $*v = 6,5×17,5 = 114*$ m/s (soit 410 km/h ! 😮). Cette valeur n’est pas réaliste. Le problème vient du fait qu’on a supposé que l’accélération est constante. Mais vous savez par expérience qu’un véhicule n’accélère pas de manière constante sur une plage de vitesse aussi grande.
TP Cinématique
- Réaliser et/ou exploiter une vidéo ou une chronophotographie pour déterminer les coordonnées du vecteur position en fonction du temps et en déduire les coordonnées approchées ou les représentations des vecteurs vitesse et accélération.
- Capacité numérique : représenter, à l’aide d’un langage de programmation, des vecteurs accélération d’un point lors d’un mouvement.
Objectif : à partir d’une vidéo, trouver les coordonnées du vecteur position d’un objet en mouvement, en déduire, par modélisation, les coordonnées des vecteurs vitesse et accélération, puis afficher sur un graphe une représentation de ces vecteurs.
Je ne vous cache pas que l’objectif de ce TP est ambitieux et que pour l’atteindre, vous allez devoir apprendre pas mal de chose. Mais vous êtes là pour ça, non ? 😊
Deux bonnes nouvelles pour ce TP : d’abord, il ressemble fort à un TP que nous avons fait en 1e (chapitre P3), donc vous ne serez pas en terrain totalement inconnu. Ensuite, il ne fait appel qu’à des logiciels libres, téléchargeables gratuitement sur internet (Regressi pour obtenir des données à partir de la vidéo, puis un tableur pour les traiter, puis Python pour afficher des graphes). Vous pourrez donc vous entraîner chez vous avec votre propre ordinateur.
1. Pointage vidéo
Commencez donc par télécharger la vidéo que nous allons exploiter, puis réalisez le pointage vidéo de la balle sur Regressi (voir le tuto sur cette page).
Attention : ne pointez la balle que si elle n’a pas de contact ni avec les mains de la joueuse, ni avec le panier.
2. Modélisation
Après avoir copier/coller les données du pointage dans un tableur, vous devez normalement avoir trois colonnes : $*t*$, $*x*$ et $*y*$. Avec ces données :
- Afficher les graphiques montrant $*x(t)*$ et $*y(t)*$, puis modélisez ces deux grandeurs (Ajouter un courbe de tendance…)
- En déduire l’expression des coordonnées des vecteurs vitesse $*\vec{v}*$ et accélération $*\vec{a}*$ en fonction du temps.
- Dans 4 nouvelles colonnes, $*v_x*$, $*v_y*$, $*a_x*$ et $*a_y*$, vous allez calculer la valeur de ces coordonnées d’après votre modélisation, pour chaque valeur de $*t*$.
- Afficher les graphiques montrant $*v_x(t)*$ et $*v_y(t)*$.
Questions
1. Que signifie, physiquement, le fait que $*v_x(t)*$ soit constant ?
2. Que signifie, physiquement, le fait que $*v_y(t)*$ change de signe au cours du mouvement ?
3. Vecteurs vitesse et accélération
Allez ! Un peu de Python maintenant… 😎
Notre objectif, dans cette partie, va être de représenter les vecteurs vitesse et accélération pour chaque position du ballon, dans un graphique montrant les positions successives du ballon (relisez cette phrase calmement… 😊).
Pour ça, il n’est pas question que je vous mâche le boulot ! Par contre, je vais mettre à votre disposition quelque petits tutos Python portant sur des tâches simples, que vous allez combiner pour arriver à vos fins.
Importer les valeurs dans Python
À la fin de l’étape précédente, nous avons obtenu les coordonnées des trois vecteurs position, vitesse, et accélération pour les différentes positions du ballon au cours de son mouvement. Comment faire pour disposer de ces valeurs dans Python ? Il n’est pas question de les rentrer à la main, nous allons utiliser la fonction text2list que j’ai créée spécialement pour vous et que vous trouverez dans la section Python. Inutile de chercher à trop l’analyser (sauf si vous êtes curieux, mais alors vous ferez ça chez vous). C’est simplement de la manipulation de chaînes de caractères et de tableaux. C’est simple, mais fastidieux.
Représenter la trajectoire du ballon
Tracer avec Python le graphique $*y(x)*$ montrant la trajectoire du ballon. Reportez-vous au tuto « Représenter un graphique » dans la section Python.
Attention, dans votre code, il va falloir tenir compte que vous voulez afficher $*y(x)*$. Or après import de vos données, vous disposez d’une liste qui a la structure suivante :
liste = [ [liste des t],
[liste des x],
[liste des y],
[liste des vx],
[liste des vy],
[liste des ax],
[liste des ay]
]
Allez, un petit rappel quand-même. Lorsqu’on veut accéder à l’élément i d’une liste appelée liste, on fait liste[i].
Représenter le vecteur vitesse
Ajouter au graphique précédent la représentation du vecteur vitesse pour chaque position du ballon. Voir le même tuto que tout à l’heure pour les vecteurs. Rappelez-vous que « chaque » en Python se dit for … in …. Cette partie va vous demander un peu plus de réflexion que la précédente. 😊
Représenter le vecteur accélération
Même principe pour le vecteur accélération. Sauf qu’ici c’est plus simple, car comme vous l’avez remarqué, le vecteur accélération est constant. Prévoyez un moyen de rendre optionnel l’affichage des vecteurs vitesse et des vecteurs accélération.
Questions
1. Que remarquez-vous à propos des vecteurs vitesse ?
2. Que remarquez-vous à propos des vecteurs accélération ?
3. Sauriez-vous refaire ce TP avec comme seule aide les tutos Python que vous avez utilisés ?
Éléments de réponses
Voici le fichier txt contenant les 7 colonnes de valeurs ($*t*$, $*x*$, $*y*$, $*v_x*$, $*v_y*$, $*a_x*$, $*a_y*$)
Le code Python permettant d’afficher la trajectoire $*y(x)*$. Attention, je n’ai pas remis la définition de la fonction txt2list
valeurs = txt2list('dossier/valeurs.txt')
import matplotlib.pyplot as plt
x = valeurs[1]
y = valeurs[2]
plt.plot(x, y, 'bo', ms = 5)
vitesse = True
acceleration = True
for k in range(len(valeurs[0])) :
if vitesse :
plt.arrow(
valeurs[1][k], # x
valeurs[2][k], # y
valeurs[3][k]/20, # vx
valeurs[4][k]/20, # vy
length_includes_head=True,
head_width=0.05,
color = 'black')
if acceleration :
plt.arrow( valeurs[1][k],
valeurs[2][k],
valeurs[5][k]/40,
valeurs[6][k]/40,
length_includes_head=True,
head_width=0.05,
color='red')
plt.show()
Quelques mouvements simples
- Caractériser le vecteur accélération pour les mouvements suivants : rectiligne, rectiligne uniforme, rectiligne uniformément accéléré, circulaire, circulaire uniforme.
Mouvement rectiligne
Un mouvement rectiligne, c’est un mouvement qui se fait… en ligne droite. En termes mathématiques, ça veut dire que la direction du vecteur vitesse ne change jamais. Mais attention, son sens peut changer si l’objet oscille (par exemple une masse que l’on suspendrait à un ressort vertical aurait un mouvement rectiligne, mais le sens de son vecteur vitesse change périodiquement au cours du temps). Pour un mouvement rectiligne quelconque, le vecteur accélération $*\vec{a}*$ a la même direction que le vecteur vitesse $*\vec{v}*$ (mais pas forcément le même sens, et il peut aussi être égal au vecteur nul !).
Un mouvement rectiligne uniforme, c’est un genre particulier de mouvement rectiligne : la vitesse de l’objet est constante. Du coup, c’est le vecteur vitesse qui est constant (direction, sens et valeur). Deuxième conséquence : comme le vecteur vitesse est constant, le vecteur accélération est… nul (rappelez-vous, $*\vec{a}*$ est la dérivée de $*\vec{v}*$).
Un mouvement rectiligne uniformément accéléré signifie que le vecteur accélération reste constant tout au long du mouvement. Un exemple de mouvement rectiligne uniformément accéléré, c’est le mouvement d’un caillou qu’on laisse tomber sans vitesse initiale. Mais nous y reviendrons dans le chapitre suivant.
Mouvement circulaire
Un mouvement circulaire, c’est… Bon, vous avez deviné ? Très bien. Pour ce qui est du vecteur accélération dans un mouvement circulaire, hé bien on ne peut rien en dire de particulier. Mais on va l’étudier plus en détails dans le paragraphe suivant avec le repère de Frenet.
Un mouvement circulaire uniforme se fait avec une valeur de vitesse constante. ✋ Attention ! J’ai bien mis le terme valeur en gras. C’est très important de le comprendre. Le vecteur vitesse, lui, change de direction tout au long du mouvement (sinon, il s’agirait d’un mouvement rectiligne uniforme). Donc $*v*$ est constant, mais pas $*\vec{v}*$ car il change de direction.
Du coup, puisque $*\vec{v}*$ n’est pas constant, sa dérivée $*\vec{a}*$ n’est pas nulle. L’objet a bel et bien une accélération.
Rappelez-vous ce que je vous disais dans le paragraphe sur l’accélération : « dès qu’un objet tourne, « accélère » ou freine, son vecteur accélération n’est pas nul. ».
En fait, le vecteur vitesse est dévié à chaque instant vers le centre de la trajectoire, car on a dit que le mouvement était circulaire. Si le mouvement est circulaire uniforme, la valeur de la vitesse ne change pas, seule sa direction change. Et dans ce cas, le vecteur accélération pointe exactement vers le centre de la trajectoire.
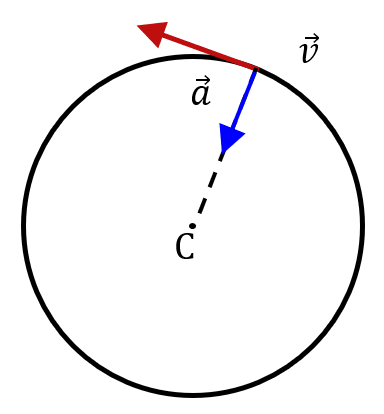
Nous allons parler un peu plus en détails des mouvements circulaires dans le paragraphe suivant