P4. Thermodynamique
La thermodynamique est la branche de la physique qui traite des phénomènes où interviennent des échanges thermiques, en particulier des transformations de l’énergie thermique en énergie mécanique.
Un système thermodynamique est constitué d’un grand nombre de particules. Pour l’étude de ce système, la thermodynamique s’intéresse à des propriétés d’ensemble et non aux comportements individuels de chaque entité (atomes, molécules…). La thermodynamique établit des relations entre des propriétés macroscopiques (pression, température, volume) sans faire intervenir les mécanismes microscopiques sous-jacents (énergie cinétique individuelle des entités qui composent le système).
Gaz parfait
- Relier qualitativement les valeurs des grandeurs macroscopiques mesurées aux propriétés du système à l’échelle microscopique.
- Exploiter l’équation d’état du gaz parfait pour décrire le comportement d’un gaz.
- Identifier quelques limites du modèle du gaz parfait.
Modèle du gaz parfait
Pour commencer, un gaz « parfait », c’est comme un corps noir, ça n’existe pas ! 😊 Mais vous le saviez déjà, car la perfection n’est pas de ce monde…
Un gaz parfait, c’est un modèle simplifié d’un gaz réel. Ce modèle permet, dans certaines conditions sur lesquelles on reviendra un peu plus loin, de décrire le comportement d’un gaz réel avec un degré de précision satisfaisant.
Que dit ce modèle ? Eh bien qu’un gaz est constitué de particules ponctuelles qui n’interagissent pas entre elles en dehors des chocs.
Équation d’état d’un gaz parfait
L’équation d’état d’un gaz parfait est la relation qui lie ses variables d’état : sa pression $*P*$, sa température $*T*$ et son volume $*V*$.
| $*P·V = n·R·T*$ | $*P*$ : pression (Pa) $*V*$ : volume (m3) $*n*$ : qdm (mol) $*R*$ : constante des gaz parfaits = 8,314 J·mol-1·K-1 $*T*$ : température (K) |
Sur l’échelle de Kelvin, 0 K = -273 °C (il s’agit du zéro absolu). Une augmentation de 1 K correspond à une augmentation de 1 °C. $µ T(\text{K}) = \theta (\text{°C}) + 273 µ$
La connaissance de deux variables d’état (et de la qdm du gaz) fixe la 3e variable d’état
Volume molaire d’un gaz parfait
1. Trouver le volume molaire, en L·mol-1 d’un gaz (considéré comme parfait) dans les Conditions Normales de Température et de Pression (CNTP) soit $*\theta*$ = 0 °C et $*P*$ = 1013,25 hPa.
2. Même question dans les Conditions Standard de Température et de Pression (CSTP) soit $*\theta*$ = 25,0 °C et $*P*$ = 1,00·105 Pa.
Correction
Le volume molaire est le volume d’une mole. Il s’agit donc de calculer $*V = \frac {nRT}P*$ avec $*n*$ = 1.Il ne faut pas oublier de convertir les températures en kelvins et les pressions en pascals.
On trouve $*V_{CNTP}*$ = 22,4 L·mol-1 et $*V_{CSTP}*$ = 24,8 L·mol-1.
Limites du modèle du gaz parfait
Le modèle du gaz parfait suppose deux choses qui sont fausses : d’une part que les molécules sont ponctuelles (c’est à dire que leur taille est négligeable devant la distance moyenne qui sépare deux molécules) et d’autre part qu’elles n’interagissent pas entre elles, c’est-à-dire qu’il n’y a pas de forces de Van der Waals entre elles.
Selon les conditions et la nature chimique du gaz, ces deux suppositions peuvent être très proches de la réalité (et donc le modèle du gaz parfait permet de faire des prévisions très proches de ce qui est effectivement constaté expérimentalement) ou pas si proches que ça…
Quand la taille des molécules n’est plus négligeable devant l’espace moyen séparant deux molécules (par exemple à basse température et pression élevée), les prévisions du modèle du gaz parfait peuvent différer assez sensiblement de ce qu’on observe expérimentalement.
De même, si l’interaction entre entités n’est pas négligeable (par exemple, dans le cas d’un gaz composé de molécules polaires) les observations expérimentales vont différer plus ou moins sensiblement des prévisions du modèle du gaz parfait.
Le domaine de validité de ce modèle dépend donc de plusieurs facteurs : d’abord bien sûr de la différence que l’on est prêt à accepter entre les prévisions de ce modèle et le comportement réel du gaz. Le domaine de validité de ce modèle sera beaucoup plus grand si on considère qu’une différence de 1 % entre les prévisions et l’expérience est acceptable, que dans le cas où on ne tolère pas plus de 0,1 % d’écart.
Ensuite, le domaine de validité dépend aussi de la nature chimique du gaz. L’hélium (petites particules, non polaires) va se comporter comme un gaz parfait dans un domaine de température et de pression beaucoup plus grand que le butanol (« grosses » molécules polaires).
Il existe d’autres modèles des gaz, ayant un domaine de validité plus large, mais plus compliqué d’un point de vue mathématique… on a rien sans rien 😊
Transferts d’énergie
- Citer les différentes contributions microscopiques à l’énergie interne d’un système.
- Prévoir le sens d’un transfert thermique.
- Distinguer, dans un bilan d’énergie, le terme correspondant à la variation de l’énergie du système des termes correspondant à des transferts d’énergie entre le système et l’extérieur.
Énergie interne d’un système
L’énergie interne (notée $*U*$) d’un système thermodynamique est l’énergie qu’il renferme. C’est une fonction d’état (c’est-à-dire qu’elle dépend des variables d’état du système) extensive (c’est-à-dire que si on double la taille du système, on double son énergie interne), associée à ce système.
Elle peut être décomposée en deux catégories :
- les énergies cinétiques, correspondant aux mouvements des particules qui le constituent, que l’on peut assimiler à l’agitation thermique ;
- les énergies potentielles dues aux interactions entre les molécules, ions, atomes, électrons, noyaux, nucléons… qui constituent ce système.
$µ U = \sum E_{\text{cin,micro}} + \sum E_{\text{pot,micro}} µ$
Étant donnée la complexité des interactions au niveau microscopique, l’énergie interne $*U*$ n’est pas calculable. On peut néanmoins calculer ses variations $*\Delta U*$.
L’énergie globale $*E_{\text{globale}}*$ d’un système est égale à son énergie mécanique macroscopique, plus son énergie interne. $µ E_{\text{globale}} = E_{\text{cin, macro}} + \sum E_{\text{pot, macro}} + U µ$
Premier principe de la thermodynamique
Selon le premier principe de la thermodynamique, lors de toute transformation, il y a conservation de l’énergie.
Le terme « principe » vient du fait que cette affirmation a toujours été vérifiée expérimentalement, mais jamais démontrée formellement de façon théorique.
Pour un système thermodynamique fermé, c’est-à-dire qui n’échange aucune matière avec l’exterieur, ce principe s’énonce de la manière suivante :
S’il n’y a pas de variation d’énergie macroscopique (c’est le cas le plus courant), alors le premier principe devient : $µ \Delta U = Q + W µ$
Toutes ces grandeurs sont algébriques (c’est-à-dire qu’elles peuvent être positives ou négatives). Pour déterminer le signe d’un transfert d’énergie, on adopte la convention dite « du banquier » : l’énergie qui sort du système est comptée négativement, tandis que celle qui rentre est comptée positivement.
Par exemple, si le transfert thermique d’un système vaut $*Q*$ = 100 J, le système a reçu 100 J.
Transferts thermiques
Un transfert thermique, c’est-à-dire un échange d’énergie thermique entre un système et le milieu extérieur, se fait toujours du corps chaud vers le corps froid. Toujours !
Il y a des dispositifs réfrigérants (frigo, congélateur, climatiseur), capable de prendre de la chaleur à un corps froid (l’intérieur du frigo) pour la céder à l’extérieur (vous avez remarqué qu’un frigo, ça chauffe à l’extérieur ?).
Mais il ne s’agit pas du tout d’un transfert spontané (il faut apporter de l’énergie électrique pour que ces sytèmes fonctionnent). Puisque les exercices sur ces sytèmes sont classiques, je vais vous exposer le principe de fonctionnement de ces systèmes.
Fonctionnement d’un frigo
Dans un frigo (ou un climatiseur), il y a au départ un gaz – qui n’a aucun rôle chimique. Le compresseur du frigo comprime fortement ce gaz, jusqu’à le liquéfier. Ce processus augmente fortement la température du fluide. On fait ensuite circuler ce fluide chaud dans un radiateur pour qu’il cède sa chaleur au milieu extérieur, jusqu’à ce qu’il retourne à la température ambiante – celle de la pièce pour un frigo, ou celle de l’extérieur pour un climateur.
Ensuite, ce fluide est décompressé peu à peu. Ce faisant, sa température diminue fortement – il repasse de l’état liquide à l’état gazeux. Ceci est bien entendu fait à proximité de l’intérieur du frigo. Comme le fluide est plus froid que l’intérieur du frigo, le transfert thermique se fait donc de l’intérieur du frigo vers le fluide.
À la fin de cette étape, le fluide est recompressé et le cycle recommence.
Le bilan global est bien le transfert d’énergie thermique d’un corps froid (l’intérieur du frigo), vers un corps chaud (le milieu extérieur). Mais ce transfert n’a rien de spontané. Il faut un apport d’énergie au frigo pour fonctionner.
Par contre, il y a deux transferts thermiques spontanés au cours du cycle : le gaz chaud comprimé transfert de la chaleur vers le milieu extérieur, puis, lors de la phase de décompression du fluide – où celui-ci est très froid, l’intérieur du frigo, qui est plus chaud que le fluide transfert de la chaleur au fluide. Ces deux transferts se font bien du chaud vers le froid.
Fonctionnement d’un frigo
1. En le justifiant rigoureusement, déterminer le signe des grandeurs $*Q_C*$, $*Q_F*$ et $*W*$ dans le cas du réfrigérateur. Préciser également la nature des sources chaude et froide en légendant le schéma ci-dessous.
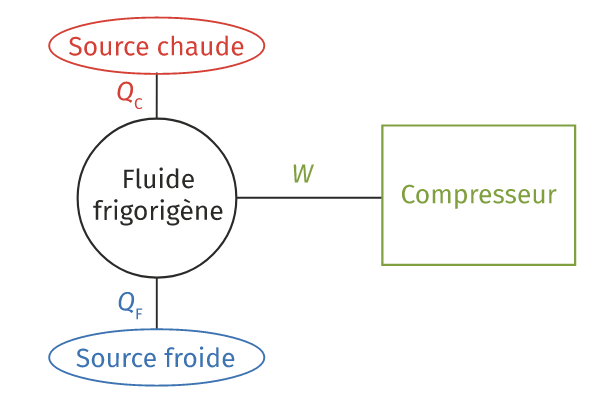
Le fluide frigorigène d’un réfrigérateur échange avec des aliments une énergie $*Q_1*$ = 104 kJ et échange avec l’extérieur une énergie $*Q_2*$ = −162 kJ.
2.a. Justifier que, au cours d’un cycle, la variation d’énergie interne du fluide est nulle.
2.b. Déterminer alors le travail mécanique $*W*$ reçu par le fluide frigorigène du réfrigérateur.
Correction
1. Le système thermodynamique étudié est le fluide frigorigène au cours de son cycle compression/décompression.
$*Q_C*$ est la chaleur cédée à la source chaude (milieu extérieur). $*Q_C*$ < 0.
$*Q_F*$ est la chaleur prise à la source froide (milieu intérieur). $*Q_F*$ > 0.
$*W*$ est le travail reçu du compresseur. $*W*$ > 0.
2.a. L’état de fluide est le même au point de départ du cycle et au point d’arrivée (sinon, il ne s’agirait pas d’un cycle. Le fluide est à la même température, à la même pression et sa nature n’a pas changé. Donc son énergie interne est la même
2.b Comme au cours d’un cycle, la variation d’énergie interne du fluide $*\Delta U*$ est nulle, alors on peut écrire que : $µ Q_C + Q_F + W = 0 µ$ et donc $*W = -Q_C -Q_F =*$ 58 kJ.
Variation d’énergie interne d’un système incompressible
- Exploiter l’expression de la variation d’énergie interne d’un système incompressible en fonction de sa capacité thermique et de la variation de sa température pour effectuer un bilan énergétique.
Très peu de choses à savoir pour cette partie. Tout tient en une seule phrase : lorsqu’un système solide ou liquide échange une chaleur $*Q*$, s’il n’y a pas de changement d’état, la variation de sa température $*\Delta T*$ (ou $*\Delta \theta*$) est proportionnelle à l’énergie échangée $*Q*$.
Mais rappelez-vous qu’une variation de $*x*$ K est égale à une variation de $*x*$ °C.
La constante de proportionnalité $*C*$, appelée capacité calorifique, dépend de la masse du système et de sa nature chimique, bien sûr. Par exemple, pour 1,0 kg d’eau liquide, elle vaut 4,2 kJ·K-1 mais pour 1,0 kg de fer, elle ne vaut que 0,44 kJ·K-1. Autrement dit, il faut presque 10 fois moins d’énergie pour chauffer du fer que pour chauffer de l’eau…
On utilise souvent la capacité calorifique massique d’une substance (par exemple 4,2 kJ·K-1·kg-1 pour l’eau). Il n’y a qu’à ensuite multiplier cette capacité calorifique massique par la masse du système pour trouver la capacité calorifique totale du système.
Mélange chaud-froid
Cette loi permet de prévoir la température d’un mélange entre un corps chaud et un corps froid, si le mélange n’échange pas de chaleur à l’extérieur.
Un exemple vaut mieux qu’un long discours. Imaginons qu’on prenne 1,0 kg d’eau à 10 °C, et qu’on plonge dans cette eau froide un morceau de fer de 50 g à une température de 95 °C. On réalise cette expérience dans un calorimètre (un genre de « thermos » particulièrement bien isolé) pour pouvoir négliger les échanges entre le système {eau - fer} avec l’extérieur. Quelle va être la température finale $*\theta_f*$ du mélange ?
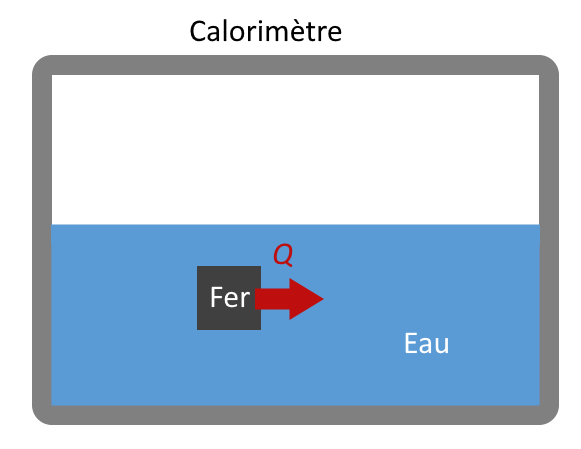
On a toutes les données pour pouvoir répondre à la question. Il faut tenir compte du fait que :
- l’énergie cédée par le fer est égale à l’énergie reçue par l’eau, car l’énergie thermique perdue par le calorimètre est considérée comme négligeable.
- le fer cède de l’énergie à l’eau jusqu’à atteindre l’équilibre thermique, c’est-à-dire jusqu’à ce que le fer ait la même température que l’eau.
Énergie thermique échangée par le fer : $*Q_1 = m_{fer}·c_{fer}·(\theta_f - 95)*$ ($*Q_1*$ < 0 car le fer cède cette énergie)
Énergie thermique échangée par l’eau : $*Q_2 = m_{eau}·c_{eau}·(\theta_f - 10)*$. ($*Q_2*$ > 0 car l’eau reçoit cette énergie)
L’énergie échangée par la totalité du système est nulle (car le système n’échange pas de chaleur avec l’extérieur). Donc $*Q_1 + Q_2 = 0*$. Du coup on obtient l’équation suivante : $µ m_{fer}·c_{fer}·(\theta_f - 95) + m_{eau}·c_{eau}·(\theta_f - 10) = 0 µ$
Sachant que $* c_{fer} *$ = 0,44 kJ·kg-1·K-1 et $*c_{eau}*$ = 4,2 kJ·kg-1·K-1, on trouve que $*\theta_f*$ = +10,4 °C
TP Capacité calorifique du cuivre
- Effectuer l’étude énergétique d’un système thermodynamique.
- Mettre en œuvre un dispositif pour réaliser un bilan énergétique et suivre l’évolution de la température d’un système.
- Mettre en œuvre un protocole permettant d’estimer une énergie transférée électriquement ou mécaniquement.
Objectif : déterminer la capacité calorifique massique du cuivre.
Données
- Capacité calorifique massique de l’eau : $*c_{eau}*$ = 4180 J·K-1·kg-1
Capacité calorifique d’un calorimètre
Un calorimètre est un récipient thermiquement très bien isolé. Il permet d’étudier des échanges de chaleur (ou énergie thermique) internes.
Cependant, même s’il n’échange qu’une chaleur négligeable avec l’extérieur, il possède une capacité thermique (faible, mais pas nécessairement négligeable). C’est-à-dire qu’il échange de l’énergie thermique avec son contenu jusqu’à avoir atteint l’équilibre thermique avec son contenu.
Pour pouvoir réaliser des mesures précises, il faut donc déterminer expérimentalement cette capacité thermique.
- Proposer un manière de déterminer expérimentalement la capacité calorifique du calorimètre dont vous disposez, en vous servant du fait que vous connaissez celle de l’eau.
- Réaliser votre expérience et calculer la capacité calorifique du calorimètre.
- Calculer la valeur en eau du calorimètre : c’est la masse d’eau qui aurait la même capacité calorifique que lui.
Capacité calorifique du cuivre
Vous disposez d’une lame de cuivre et de tout le matériel du laboratoire dont vous avez besoin.
- Proposer un protocole pour déterminer le plus précisément possible la capacité calorifique massique du cuivre.
- Réaliser votre mesure expérimentale en estimant les incertitudes associées.
Chauffe-eau
1. Calculer l’énergie nécessaire pour chauffer l’eau nécessaire pour une douche (50 L). L’eau est chauffée de 10 °C à 40 °C ($*c_{eau}*$ = 4,2 kJ·kg-1·K-1).
2. En fait, l’eau qui sort du chauffe-eau a une température de 60 °C. Elle est mélangée à de l’eau froide à 10 °C. Quel est le volume d’eau chaude consommée pour une douche ?
Correction
1. $*E*$ = 50×4,2×(+30) = 6300 kJ.
2. Si on suppose qu’il n’y a pas de perte de chaleur vers l’extérieur, l’échange thermique ne se fait qu’entre l’eau chaude et l’eau froide. On peut donc écrire :
$µ m_C·c_{eau}·(-20) + m_F·c_{eau}·(+30) = 0 µ$
avec $*m_C*$ la masse d’eau chaude et $*m_F*$ la masse d’eau froide.
On a deux inconnues $*m_C*$ et $*m_F*$, il nous faut donc une 2e équation. On se sert du fait qu’une douche nécessite 50 L d’eau, donc $*m_c + m_F*$ = 50.
On obtient donc l’équation :
$µ m_C×(-20) + (50 - m_C)×30 = 0 µ$
d’où $*m_C*$ = 30 kg, soit 30 L.
Révision & entraînement
Échauffement d’un gaz par compression
Vous savez par expérience que lorsqu’on comprime un gaz, sa température augmente. On va s’intéresser dans cet exercice à ce phénomène.
Un gaz est placé dans un cylindre de 5,0 cm de diamètre et de profondeur $*h*$ = 10 cm. Sa pression initiale $*P_0*$ est égale à la pression atmosphérique (1,0·105 Pa). Il peut être comprimé par action d’un piston (exactement comme dans une seringue bouchée). On exerce une force $*F*$ = 150 N sur ce piston (en plus de la poussée exercée par la pression atmosphérique), ce qui a pour effet de le faire avancer d’une distance $*d*$, jusqu’à ce que la pression interne du gaz $*P_f*$ soit en équilibre avec la pression exercée par le piston (ajoutée à celle de l’air extérieur).
La température initiale du gaz vaut $*\theta_0*$ = 20 °C.
1.a. Rappeler la relation entre pression, force et surface.
1.b. Calculer la pression d’équilibre finale du gaz sous l’effet de la compression du piston.
1.c. Peut-on déduire, à partir de la loi des gaz parfaits, quel sera le volume du gaz dans cet état ? Justifier
Puisque la loi des gaz parfaits ne peut pas nous aider ici, il faut faire appel à une autre loi, qui n’est pas au programme.
Lors d’une compression adiabatique d’un gaz parfait (c’est-à-dire une compression sans échange de chaleur avec le milieu extérieur), la loi de Laplace dit que :
$µ PV^{\gamma} = \text{constante} µ$
Pour l’air, l’indice adiabatique $*\gamma*$ vaut 1,40.
On va ici négliger les échanges thermiques entre le gaz (qui est de l’air) et l’ensemble {cylindre + piston} pour pouvoir appliquer la loi de Laplace.
2.a. Calculer le volume du gaz après la compression.
2.b. Calculer la distance $*d*$
2.c. En déduire le travail fourni par le piston.
3. Calculer la température finale $*T_f*$ du gaz.
Correction
1.a. $*P = \cfrac FS*$
1.b. La force exercée par le piston vaut 150 N.
Sa surface vaut $*S*$ = π×0,0252 = 1,96·10-3 m2.
La pression du gaz est donc égale à la pression exercée par le piston due à la force de 150 N, plus la pression atmosphérique (qui pousse également sur le piston).
$*P_1*$ = 150÷2,0·10-3 + 1,0·105 = 1,76·105 Pa.
1.c. Non, car on ne connaît ni son volume, ni sa température (on peut par contre calculer la qdm initiale $*n*$ grâce aux données du problème.
2.a. D’après la loi de Laplace, on a $*P_0V_0^{\gamma} = P_1V_1^{\gamma}*$
D’où on obtient que :
$µ V_1 = V_0 \sqrt[\gamma]{\frac{P_0}{P_1}} µ$
$*V_0*$ = $*S·h*$ = 2,0·10-3×0,10 = 0,196 L
donc $*V_1*$ = 0,130 L
2.b. $*d = h - \cfrac {V_1}S =*$ 3,33 cm
2.c. $*W*$ = 150×3,33·10-2 = 5,00 J
3. Il faut d’abord calculer la qdm de gaz : $*n = \cfrac {P_0V_0}{RT_0}= \cfrac {10^5×1,96·10^{-4}}{8,314×293}*$
d’où $*n*$ = 8,06·10-3 mol.
Donc $*T_f = \cfrac{P_1V_1}{nR} =*$ 345 K, soit 72 °C (ça chauffe bien… 😊)