P6. Ondes
Un tout nouveau thème dont nous allons parler sur les deux prochains chapitres. Révisez le chapitre P6 de première pour vous rafraîchir la mémoire.
Ondes sonores
- Exploiter l’expression donnant le niveau d’intensité sonore d’un signal.
- Capacité mathématique : utiliser la fonction logarithme décimal et sa fonction réciproque.
Qu’est-ce que le son ?
Le son, c’est une vibration de l’air (ou plus généralement du milieu matériel dans lequel le son se propage, car le son ne se propage pas que dans l’air…) qui se propage. Les ondes sonores font partie de la grande famille des ondes mécaniques, c’est-à-dire des ondes liées à une déformation de la matière.
Un son (ou onde sonore) est produit par une perturbation qui fait se déplacer la matière de part et d’autre de sa position d’équilibre. C’est une onde périodique (pas forcément sinusoïdale) de fréquence comprise entre 20 Hz et 20 kHz (en dehors de ces limites, il s’agit d’infrason ou d’ultrason).

Cette perturbation va créer des zones de plus forte densité de particules (haute pression) et des zones de plus faible densité de particules (faible pression).
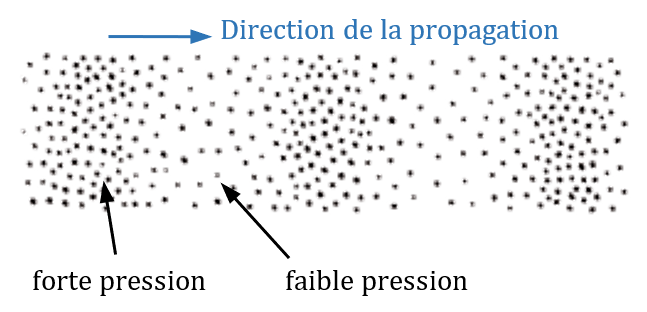
Ondes mécaniques (rappel)
Lorsqu’on perturbe mécaniquement de la matière (c’est-à-dire lorsqu’on la déforme ou qu’on la comprime), cette perturbation peut se propager à cause des propriétés élastiques de la matière. Par exemple, si vous tendez une corde et que vous créez un mouvement rapide vertical d’une de ces extrémité, cette perturbation va se propager tout au long de la corde.

Tout est une question d’échelle. Le verre est tout de même élastique, tant qu’on reste dans son (faible) domaine d’élasticité. Le verre peut donc vibrer ce qui signifie que le son peut se propager dans le verre. C’est le cas de toutes les matières, même celles qui ne nous paraissent pas élastiques ou compressibles (la roche, le verre…)
Notez bien que lorsqu’elle est parcourue par une onde mécanique, la matière ne se déplace pas. En tout cas pas de manière permanente. Les molécules oscillent autour d’une position moyenne, mais cette position moyenne ne change pas. Par contre, une onde transporte de l’énergie.
Intensité et niveau sonore
Une source sonore est caractérisée par la puissance sonore $*P*$ qu’elle émet, en watt.
Cette puissance est émise dans toutes les directions, transportée par l’onde sonore, et se « dilue » sur la surface de la sphère d’émission qui grandit à mesure que le son se propage (on suppose que cette puissance est émise de manière égale dans toutes les directions de l’espace – dans la pratique, c’est rarement le cas).
L’intensité $*I*$ d’un son correspond à une puissance sonore par unité de surface. $*I*$ s’exprime en W·m-2. Plus on se trouve loin de la source, plus l’intensité sonore perçue est faible.
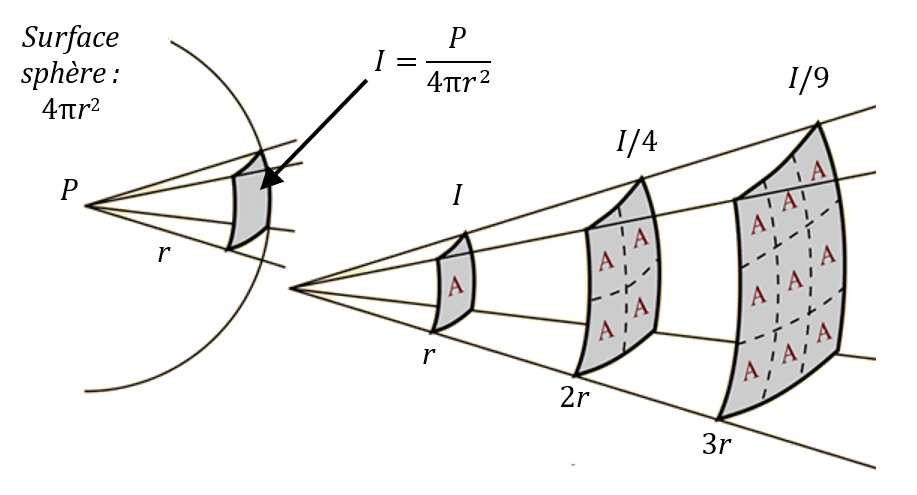
Lorsqu’on se trouve à une distance $*r*$ de la source, la puissance sonore $*P*$ est répartie sur une surface de $*4\pi r^2*$.
Lorsqu’on se trouve à une distance deux fois plus grande, la même puissance est répartie sur une surface 4 fois plus grande $*4\pi (2r)^2*$. L’intensité sonore est donc 4 fois plus faible.
L’intensité sonore ne reflète cependant pas la perception « biologique » qu’on peut avoir d’un son. Pour le dire de manière approximative, si vous doublez l’intensité d’un son, vous n’aurez pas l’impression que le son est « deux fois plus fort ». C’est parce que la perception d’un son est « logarithmique ». Autrement dit, vous aurez une impression de son « deux fois plus fort » si le logarithme de l’intensité sonore a doublé. C’est pour ça qu’on a définit, en plus de l’intensité sonore (noté $*I*$), le niveau sonore (noté $*L*$).
Le niveau sonore $*L*$ d’un son d’intensité $*I*$ s’exprime en décibel (dB) et se calcule grâce à la relation suivante :
| $µ L = 10·\log \left( \frac I{I_0} \right)µ$ |
$*L*$ : niveau sonore (dB) $*I*$ : intensté sonore (W·m-2) $*I_0*$ : intensité sonore de référence (10-12 W·m2) |
$*I_0*$ correspond plus ou moins au son le plus faible qui soit perceptible (mais ça dépend de la fréquence du son et des capacités auditives de la personne, bien sûr).
Pour calculer l’intensité sonore connaissant le niveau sonore, on utilise la fonction réciproque du log (ici sous-entendu le logarithme décimale log10).
| $µ I = I_0·10^{\frac L{10}}µ$ | $*L*$ : niveau sonore en dB $*I*$ : intensité sonore en W·m-2 $*I_0*$ : intensité de référence = 10-12 W·m-2 |
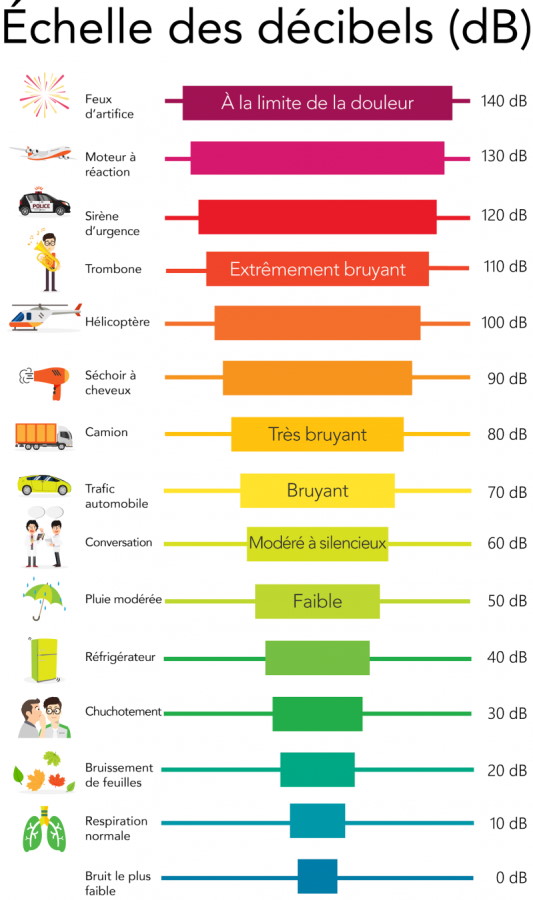
À partir de 85 dB, la loi estime qu’une durée d’exposition prolongée peut présenter un risque pour l’audition. Ce risque est d’autant plus grand que la durée d’exposition est grande (5 h par semaine à 89 dB, 1h45 par semaine à 100 dB).
Niveau sonore
Une personne parle avec un niveau sonore perçu à 1 m égal à 60 dB. Quel est le niveau sonore total si une deuxième personne se met à parler en même temps à la même distance avec la même intensité sonore ?
Correction
On ne peut ajouter que des intensités sonores. 60 dB correspond à une intensité sonore de 10-12×106 = 10-6 W·m-2. S’il y a deux sources sonores identiques, l’intensité sonore est doublée. Donc le niveau sonore correspondant vaut : $µ L = 10 \log \frac{2·10^{-6}}{10^{-12}} = 63,0 \; \mathrm{dB} µ$
Ce résultat est intéressant à retenir. Doubler un grandeur correspond à une variation de 3,0 dB car 10·log(2) ≃ 3,0.
Atténuation du son
À mesure que l’on s’éloigne d’une source sonore, le son perçu est de plus en plus faible. Il y a deux raisons totalement indépendantes à ce phénomène.
Dilution de l’énergie sonore dans l’espace
Imaginons un petit pétard (assimilé à un point) qui explose en l’air, loin de tout obstacle tel que des murs ou le sol (on reverra plus tard pourquoi je précise ça maintenant). L’explosion du pétard crée une onde sonore d’une certaine puissance et cette onde se propage dans toute les directions. La figure géométrique formée par le « front d’onde », c’est-à-dire la première vague de surpression, est une sphère (on dit que l’onde est sphérique).
La puissance de cette première « vague de pression » a une certaine valeur, et à mesure que l’onde se propage, cette puissance se trouve répartie sur une surface (la surface de la sphère qui correspond au front d’onde) de plus en plus grande.
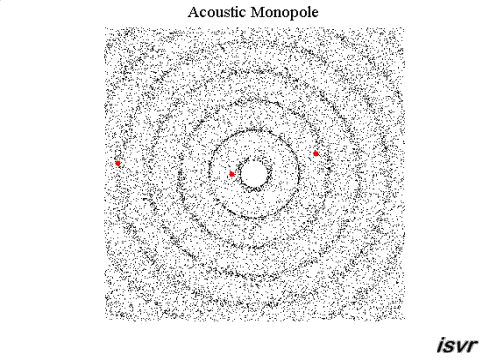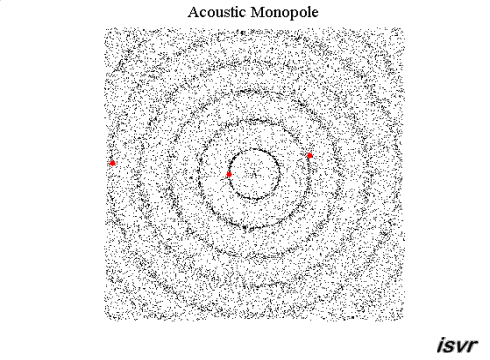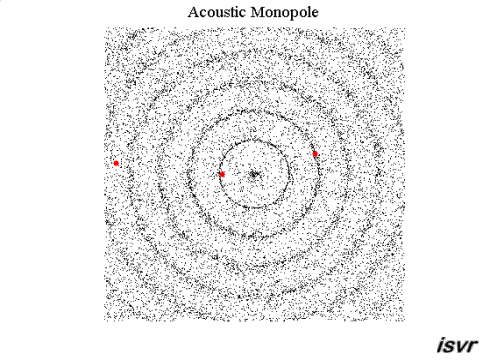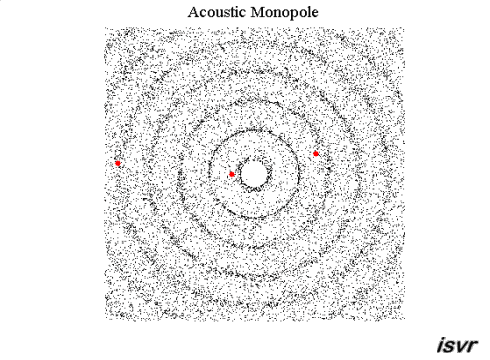
La surface d’une sphère $* 4\pi R^2 *$ est proportionnelle au carré de son rayon $*R*$. Donc l’intensité sonore est inversement proportionnel au carré de la distance entre la source et le récepteur.
Atténuation et distance
1. Démontrer formellement la phrase « l’intensité sonore est inversement proportionnel au carré de la distance entre la source et le récepteur ».
2. Calculer l’atténuation du niveau sonore d’un son se propageant dans l’air sans dissipation d’énergie et en l’absence de tout phénomène de réflexion (donc la situation dans laquelle on s’est placé dans le cours un peu plus haut), lorsque la distance source-récepteur est doublée.
Correction
1. L’intensité sonore, c’est la puissance $*P*$ de la source sonore (supposée constante), répartie sur la surface de la sphère dont le centre correspond à la position de la source et dont le rayon $*R*$ correspond à la distance à laquelle on se trouve de la source. $µ I = \frac P{4\pi R^2} µ$
On voit que $*I*$ varie en $*\frac 1{R^2}*$, c’est-à-dire que $*I*$ est proportionnel à l’inverse de $*R*$ au carré.
2. Calculons l’atténuation lorsqu’on passe d’une distance $*R*$ à une distance $*2R*$ de la source. Il suffit d’exprimer $*L*$ en fonction de $*I*$ à une distance $*R*$ puis à une distance $*2R*$ : $µ \begin{aligned} L(R) &= 10 \log \frac P{4\pi R^2·I_0} \\ L(2R) &= 10\log \frac P{16\pi R^2·I_0} \end{aligned} µ$ Donc la variation du niveau sonore vaut : $µ \begin{aligned} L(2R) - L(R) &= 10\log \frac P{16\pi R^2·I_0} - 10 \log \frac P{4\pi R^2·I_0} \\ &= 10 \log \left( \frac P{16\pi R^2·I_0}·\frac {4\pi R^2·I_0}P \right) \\ &= 10 \log \left( \frac 14 \right) \\ &= -\, 6 \; \mathrm{dB} \end{aligned} µ$
On constate que cette atténuation ne dépend pas de $*R*$ : à chaque fois qu’on double la distance source – récepteur, on perd 6 dB.
Absorption de l’énergie sonore par la matière
En plus de la simple « dilution » géométrique de la puissance d’une onde sonore, la matière absorbe une partie de l’énergie sonore qui la traverse et la transforme en chaleur. Ce phénomène est complexe, il dépend de nombreux facteurs (nature de la matière, fréquence du son, température, etc). On n’entrera pas dans les détails, mais sachez qu’il existe. Il est mis à profit dans les isolations acoustiques.
TP Niveau sonore et atténuation
- Mesurer un niveau d’intensité sonore.
- Illustrer l’atténuation géométrique et l’atténuation par absorption.
Objectif du TP : étudier l’atténuation du niveau sonore en fonction de la distance à la source, ainsi que l’atténuation sonore par absorption.
Matériel
- Une source sonore de puissance constante
- Un sonomètre
Travail demandé
- Tracer un graphique illustrant l’évolution du niveau sonore $*L*$ en fonction de la distance à la source sonore. L’idéal est de réaliser les mesures en milieu ouvert, avec un son de fréquence pas trop basse (800 à 1000 Hz) et d’une intensité importante pour pouvoir négliger les bruits ambients. Réaliser les mesures sur des distances assez courtes (entre 25 cm et 2,5 m de la source sonore.
- Évaluer l’effet d’un matériau absorbant (mousse ou polystyrène expansé) sur le niveau sonore reçu. Pour cela, l’idéal est de placer la source sonore dans la pièce voisine, juste en face de la porte de communication entre cette pièce et la salle de TP. Mettre en évidence la diminution du niveau sonore lorsque la porte est fermée. Mettre en évidence que cette diminution dépend assez sensiblement de la fréquence du son émis par la source.
Éléments de réponses
Dans notre situation, on a une atténuation d’environ -0,16 dB·cm-1
L’expérience de la mesure de l’atténuation par la porte montre que l’atténuation est comprise entre -5 dB et -20 dB environ, selon la fréquence du son. Il n’y a cependant pas de lien clair entre la fréquence et l’atténuation par la porte.
Casque anti-bruit
Sur un chantier, une personne se trouve à 1 m d’un engin dont la puissance sonore est de 15 mW.
1. Préciser s’il y a danger pour cette personne, c’est-à-dire si $*L*$ > 90 dB.
2. Un casque anti-bruit dont l’atténuation est de -20 dB peut-il protéger cette personne ?
3. Y a-t-il danger à 10 m de l’engin si on ne porte pas de casque anti-bruit ?
Correction
1. $*I = \frac P{4\pi R^2} = *$ 1,19 mW·m-2 soit $*L*$ = 90,8 dB. On est légèrement au-dessus du seuil de danger.
2. Avec un casque de protection, le niveau passe à 70,8 dB, donc il n’y a plus de danger.
3. À 10 m de l’engin, on a $*L*$ = 70,8 dB. Pas de danger sans casque anti-bruit.
Réduction active de bruit
La réduction active de bruit consiste à supprimer le bruit résiduel dans les oreillettes d’un casque audio grâce à l’injection d’un son appelé « anti-bruit ». Le graphique ci-dessous présente le niveau d’intensité sonore mesurée en fonction de la fréquence dans les situations suivantes :
- niveau d’intensité sonore ambiant à proximité immédiate du casque (cas n°1) ;
- niveau d’intensité sonore entre les oreillettes lorsque le dispositif actif est éteint et que les oreillettes interviennent seules (cas n°2) ;
- niveau d’intensité sonore entre les oreillettes lorsque le dispositif actif fonctionne (cas n°3).
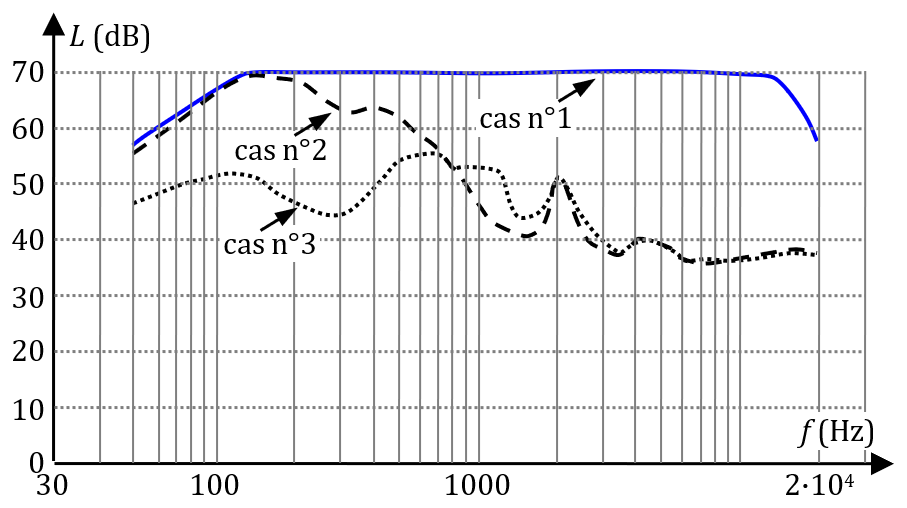
Identifier approximativement les domaines de fréquence pour lesquels :
- seules les oreillettes sont efficaces pour la réduction de bruit ambiant ;
- seul le dispositif actif est efficace pour la réduction du bruit ambiant ;
- les deux dispositifs participent à la réduction du bruit ambiant.
Correction
• Seules les oreillettes sont efficaces : les courbes n°2 et 3 sont confondues (ou la courbe n°3 est au-dessus de la courbe n°2), c’est-à-dire où la réduction active de bruit n’apporte rien (voire génère du bruit). C’est le cas au-delà de 700 Hz.
• Seul le dispositif actif est efficace : les courbes n°1 et 2 sont confondues, c’est-à-dire où les oreillettes ne diminuent aucunement le bruit extérieur. C’est le cas dans les basses fréquences jusqu’à 150 Hz environ.
• Les deux dispositifs participent à la réduction : la courbe n°3 est situé sous la courbe n°2 et la courbe n°2 est située sous la courbe n°1. C’est le cas entre 150 et 700 Hz.
Diffraction
- Caractériser le phénomène de diffraction dans des situations variées et en citer des conséquences concrètes.
- Exploiter la relation exprimant l’angle caractéristique de diffraction en fonction de la longueur d’onde et de la taille de l’ouverture.
TP Diffraction
- Illustrer et caractériser qualitativement le phénomène de diffraction dans des situations variées.
- Exploiter la relation donnant l’angle caractéristique de diffraction dans le cas d’une onde lumineuse diffractée par une fente rectangulaire en utilisant éventuellement un logiciel de traitement d’image.
Objectifs du TP :
- Étudier le phénomène de diffraction
- Exploiter ce phénomène pour déterminer l’épaisseur d’un cheveu
Matériel disponible
- un laser
- un écran
- un jeu de fils de différent diamètre (en µm) : 38 ; 50 ; 76 ; 100 ; 120 ; 150
Expérience préalable
- Installer le laser et l’écran à environ deux à trois mètres de distance, de manière à obtenir le spot lumineux au milieu de l’écran.
- Placer un fil sur le chemin du rayon, à environ 10 cm de la source laser.
- Observer ce qu’il se passe sur l’écran.
1. Qu’est-ce qu’on s’attend à obtenir a priori sur l’écran ?
Le fait que l’on obtienne pas ce qu’on attend a priori met en évidence le phénomène de la diffraction. Ce phénomène est propre aux ondes.
2. Quelle est l’influence du diamètre du fil sur ce phénomène (c’est-à-dire sur la largeur de la tache centrale) ? Une réponse qualitative est attendue.
3. De quelle autre grandeur physique modifiable sur votre montage dépend la largeur de la tache centrale ?
Modélisation du phénomène
- Trouver la loi mathématique reliant l’importance du phénomène de diffraction (que l’on quantifiera par la largeur de la tache centrale $*\ell*$) au diamètre du fil $*a*$.
Conseils pour la réalisation de vos mesures
-
La figure ci-dessous vous indique comment mesurer la largeur de la tache centrale.

La taille de la tache centrale se mesure entre les milieux des zones sombres qui l’entourent - Pour être le plus précis possible, vous disposerez le montage de manière à ce que votre tache centrale soit la plus large possible (voir question 3).
Exploitation de la diffraction pour mesure le diamètre d’un cheveu
- En mesurant la largeur de la tache centrale produite par la diffraction par un cheveu, en déduire son diamètre.
- Vérifier que ce diamètre correspond bien à la réalité, grâce à un microscope et une lame de Malassez.
Éléments de réponses
Lorsqu’on trace le graphique montrant la largeur de la tache centrale $*\ell*$ en fonction de l’épaisseur $*a*$ du fil, on obtient la figure suivante
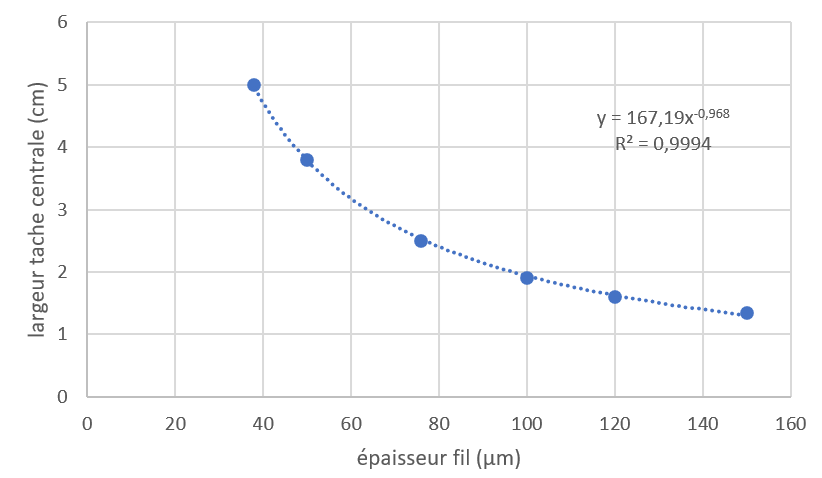
On voit que la largeur de la tache centrale est inversement proportionnelle à l’épaisseur du fil.
À partir de là, on peut déduire l’épaisseur d’un cheveu de la largeur de la tache centrale qu’il crée dans les mêmes conditions, soit par lecture graphique, soit en utilisant le modèle mathématique proposé par le tableur.
Qu’est-ce que la diffraction ?
Ce qu’en dit Wikipédia
La diffraction est le comportement des ondes lorsqu’elles rencontrent un obstacle ou une ouverture. Ce phénomène peut être interprété par la diffusion d’une onde par les points de l’objet.
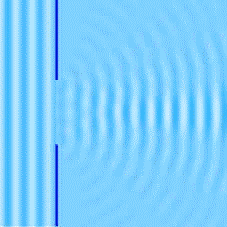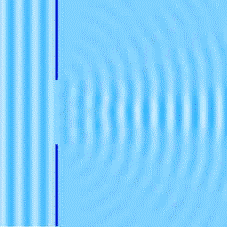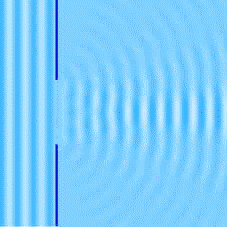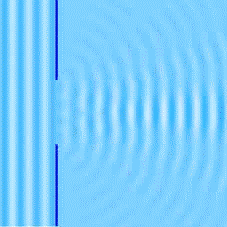
La diffraction s’observe avec la lumière, mais de manière générale avec toutes les ondes : le son, les vagues, les ondes radio, les rayons X, etc. Elle permet de mettre en évidence le caractère ondulatoire d’un phénomène et même de particules matérielles tels que des électrons, neutrons, atomes froids, etc.
Dans le domaine de l’étude des phénomènes de propagation des ondes, la diffraction intervient systématiquement lorsque l’onde rencontre un objet qui entrave une partie de sa propagation (typiquement le bord d'un mur ou le bord d'un objectif). Elle est ensuite diffractée avec d'autant plus d'intensité que la dimension de l'ouverture qu'elle franchit se rapproche de sa longueur d'onde : une onde type radio sera facilement diffractée par des bâtiments dans une ville, tandis que la diffraction lumineuse y sera imperceptible.
Source : Wikipédia


Taille de l’obstacle et ouverture
La diffraction est donc le phénomène d’éparpillement ou de déviation des ondes par les bords d’une ouverture ou d’un obstacle. L’importance du phénomène de diffraction dépend de la taille de l’obstacle ou de l’ouverture qu’elle rencontre par rapport à sa longueur d’onde. Plus l’obstacle est petit, plus le phénomène de diffraction sera marqué – mais, et c’est plus embêtant, plus la fraction de l’onde diffractée sera petite (donc moins perceptible).

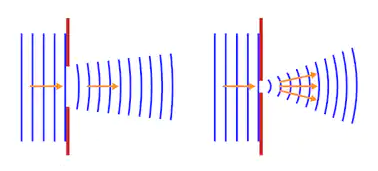
L’angle d’ouverture du faisceau dû à la diffraction est lié à la taille de l’obstacle et à la longueur d’onde de l’onde diffracté par la relation suivante :
| $µ\theta = \dfrac \lambda a µ$ |
$*\theta*$ : ouverture du faisceau principal (radian) $*\lambda*$ : longueur d’onde de l’onde diffracté $*a*$ : plus petite taille de l’obstacle |
La figure ci-dessous est obtenue par diffraction d’un faisceau laser par une fente rectangulaire. On observe qu’il y a une tache centrale plus lumineuse, accompagnée de part et d’autre d’autres taches plus petites et moins lumineuses.

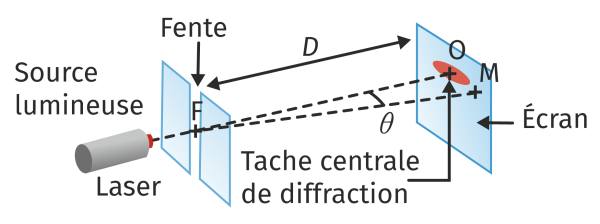
Ce qu’on appelle « ouverture du faiseau principal », c’est l’angle $*\theta*$ indiqué sur la figure ci-dessous. Sur cette figure, seuls le faisceau principal et la tache centrale sont représentés. La largeur de la tache centrale est notée $*\ell*$.
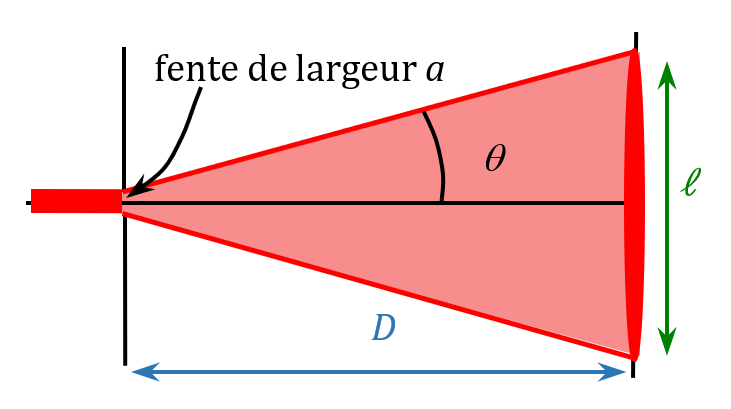
Diffraction et longueur d’onde
Les ondes radio sont divisées en différentes « bandes » qui dépendent de leur longueur d’onde ou de leur fréquence. Les « grandes ondes » (LW) de radiodiffusion ont une fréquence comprise entre 150 et 300 kHz, alors que la bande FM s’échelonne entre 88 et 108 MHz.
Quelle bande d’onde capte-t-on mieux au milieu d’un tunnel ? Justifier qualitativement et quantitativement
Correction
Les ondes FM seront moins diffractées que les ondes LW car la taille de l’ouverture du tunnel est comparativement beaucoup plus grande pour les ondes FM que pour les ondes LW (de fréquence plus faible que les ondes FM). Comme les ondes FM sont moins diffractées, elles sont donc moins déviées et pénètreront moins profondément dans le tunnel. C’est donc les ondes LW qui seront mieux captées.
Tache centrale de diffraction
Reprenons la figure du cours montrant l’ouverture du faisceau de diffraction.

1. Trouver la relation liant les grandeurs $*\ell*$, $*\theta*$ et $*D*$.
2. En vous servant du fait que $*\theta*$ est très petit et donc que $*\tan \theta \simeq \theta*$ lorsque $*\theta*$ est exprimé en radian, donner l’expression de $*\ell*$ en fonction de $*\theta*$, $*D*$ et $*a*$.
Correction
1. On voit sur la figure que le côté opposé à $*theta*$ mesure $*\frac {\ell}2 *$. Donc $* \tan \theta = \frac {\ell/2}D*$ soit $* \tan \theta = \frac {\ell}{2D}*$.
2. Si $*\theta*$ est très petit, on a : $* \theta = \dfrac {\ell}{2D}*$. Or on sait que $*\theta = \dfrac \lambda a *$ donc $* \dfrac \lambda a = \dfrac {\ell}{2D} *$
d’où $* \ell = \dfrac {2 \lambda D}a *$.
Mesure du diamètre d’un fil
On cherche à déterminer le diamètre d’un fil par diffraction. On place ce fil sur le trajet d’un faisceau laser de longueur d’onde $*\lambda*$ = 632,8 nm. On recueille sur un écran la figure de diffraction due au fil. Cet écran est placé à une distance $*D*$ = 2,00 m ± 5 mm. On mesure la taille de la tache centrale de diffraction et on trouve 2,1 cm ± 2 mm.
Déterminer le diamètre du fil, ainsi que l’incertitude portant sur cette mesure. On considère que l’incertitude portant sur $*\lambda*$ est négligeable.
Correction
On peut se servir du résultat de l’exercice précédent : $* \ell = \dfrac {2 \lambda D}a *$.
Donc $* a = \dfrac {2 \lambda D}\ell \simeq *$ 121 µm
Pour trouver l’incertitude sur le diamètre du fil, on utilise le fait que l’incertitude relative sur un grandeur calculée est la moyenne géométrique de l’incertitude des autres grandeurs :
$µ \begin{aligned}
\frac {\Delta a}a &= \sqrt{\left(\frac{\Delta D}D\right)^2 + \left(\frac{\Delta \ell}\ell\right)^2} \\
&= \sqrt{\left(\frac{0,005}2\right)^2 + \left(\frac{2}{21}\right)^2}
\end{aligned}µ$
D’où $*\frac {\Delta a}a*$ ≃ 10 %
Le diamètre du fil est donc de 121 µm ± 12 µm
Interférences
- Caractériser le phénomène d’interférences de deux ondes et en citer des conséquences concrètes.
- Établir les conditions d’interférences constructives et destructives de deux ondes issues de deux sources ponctuelles en phase dans le cas d’un milieu de propagation homogène.
- Prévoir les lieux d’interférences constructives et les lieux d’interférences destructives dans le cas des trous d’Young, l’expression linéarisée de la différence de chemin optique étant donnée. Établir l’expression de l’interfrange.
- Exploiter l’expression donnée de l’interfrange dans le cas des interférences de deux ondes lumineuses, en utilisant éventuellement un logiciel de traitement d’image.
- Capacité numérique : représenter, à l’aide d’un langage de programmation, la somme de deux signaux sinusoïdaux périodiques synchrones en faisant varier la phase à l’origine de l’un des deux.
Superposition d’ondes
Lorsque deux ondes de même nature (par exemple deux ondes sonores, ou deux ondes électromagnétiques) passent en un même point, elles se superposent (et continuent ensuite à se propager sans être le moins du monde affectées par cette rencontre – elles ne sont pas déviées l’une sur l’autre par exemple).
Ça veut dire qu’en ce point, la perturbation totale $*S(t)*$ – c’est-à-dire la valeur de la grandeur modifiée par le passage de l’onde, comme la pression de l’air pour une onde sonore, ou encore le champ électrique pour une onde électromagnétique – la perturbation totale $*S(t)*$ donc, est la somme algébrique des perturbations dues à chacune des ondes : $*S(t) = s_1(t) + s_2(t)*$

Quand on dit « algébrique », ça veut dire que ça peut être positif ou négatif. Autrement dit, si en un point, $*s_1(t)*$ = $*-s_2(t)*$, la superposition de ces deux ondes en ce point et à cet instant va être… nulle. 😅
Autrement dit, une onde + une autre onde, dans certain cas, ça peut être égale à une absence d’onde ! 😵

Alors bien sûr, tout ça se passe très vite. On ne peut pas observer quoique ce soit lorsque, de manière ponctuelle, deux ondes s’ajoutent ou s’annulent en un point. Sauf… quel suspens ! 😊
Sauf si on est en présence d’ondes périodiques de même fréquence (et de même nature, bien sûr… une onde électromagnétique ne peut bien évidemment pas s’ajouter à une onde sonore).
Imaginons deux ondes qui se propagent en sens inverse. Si ces deux ondes ont la même fréquence, alors sur certains points du trajet, l’une va toujours annuler l’autre, tandis que sur d’autres, les deux vont toujours s’amplifier – ce n’est pas très rigoureux ce que je viens d’écrire, mais c’est pour vous faire « sentir » les choses dans un premier temps.
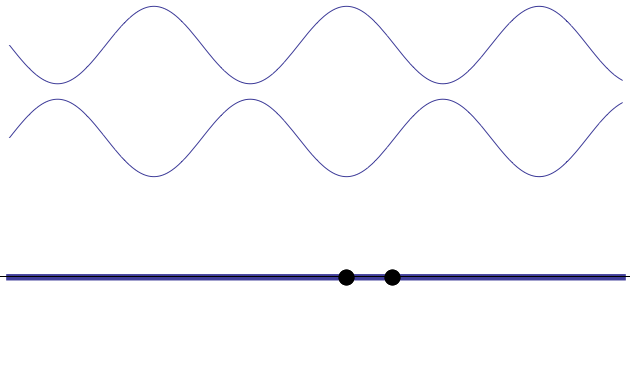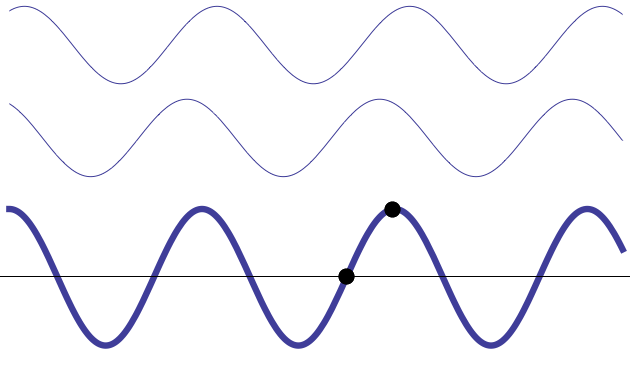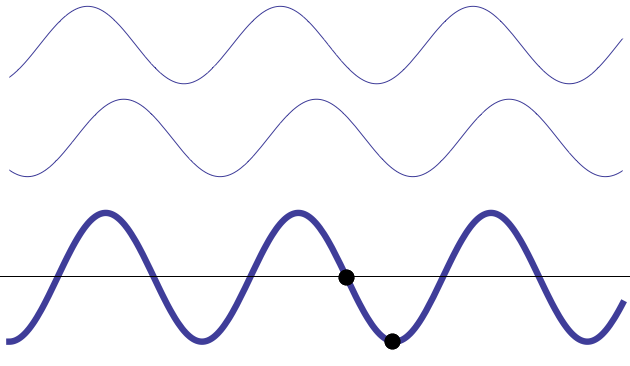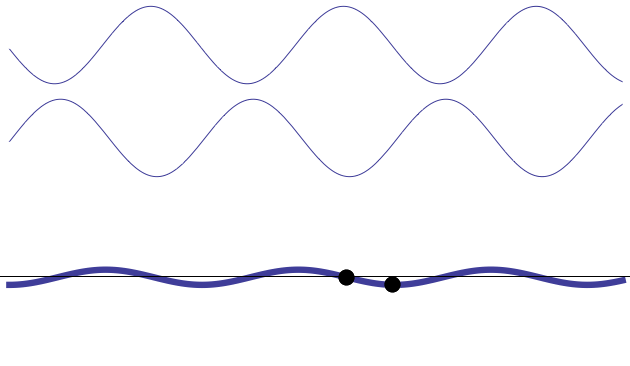
On voit que au niveau du point à gauche (appelons-le P1), les ondes arrivent de telle manière qu’à tout instant, $*s_1(t) + s_2(t) = 0*$. J’insiste sur le « à tout instant ». C’est ça qui va permettre de percevoir l’annulation de ces ondes. Et ce n’est possible que si les ondes ont la même fréquence. Et bien sûr ça n’arrive qu’en certains points, pas partout.
Au niveau du point de droite (P2), celui-ci est situé à une position où la somme $*s_1(t) + s_2(t)*$ a une amplitude maximale.
On dit qu’en P1, les ondes sont en opposition de phase, alors qu’en P2, elles sont en phase.


J’y viens… Mais avant, un petit exercice !
Superposition d’onde
Imaginons deux ondes de même nature arrivant en un point P. La première crée un perturbation $*s_1(t) = \sin t*$ et la deuxième une perturbation $*s_2(t) = \sin 1,5t*$. L’intensité d’une onde dépend de la valeur moyenne du carré de son amplitude.
1. Tracer un graphique montrant la résultante $*S(t) = s_1(t) + s_2(t)*$ pour $*t*$ variant entre 0 et 65 s. L’intensité de l’onde résultante est-elle nulle ?
2. Même question si $*s_2(t) = \sin (1,5t+\pi)*$ ($*s_1*$ ne change pas).
3. Même question si $*s_2(t) = \sin t*$ ($*s_1*$ ne change pas).
4. Même question si $*s_2(t) = \sin (t+\pi)*$ ($*s_1*$ ne change pas). Conclure.
Correction
1. Graphique obtenu en prenant un point toutes les 0,1 s.
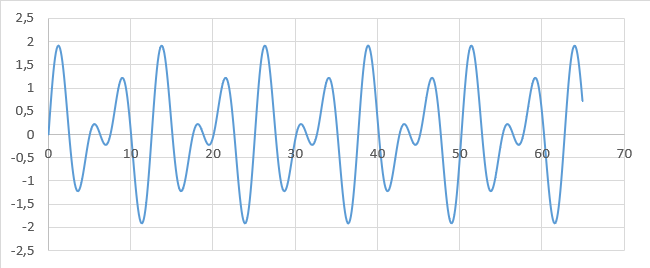
On constate que la valeur moyenne du carré de l’amplitude de la superposition n’est pas nulle, donc l’intensité de l’onde résultante n’est pas nulle.
2. Graphique obtenu pour $*s_2(t) = \sin (1,5t+\pi)*$.
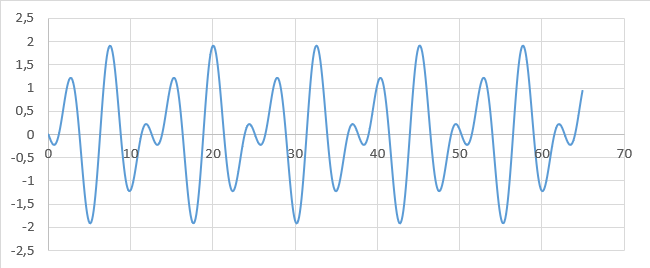
On constate que la valeur moyenne du carré de l’amplitude de la superposition n’est pas nulle, donc l’intensité de l’onde résultante n’est pas nulle.
3. Graphique obtenu pour $*s_2(t) = \sin (t)*$.
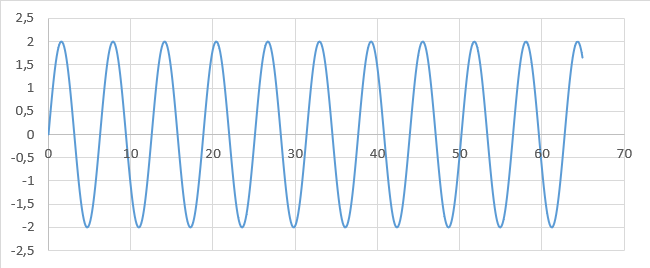
On constate que la valeur moyenne du carré de l’amplitude de la superposition n’est pas nulle, donc l’intensité de l’onde résultante n’est pas nulle.
4. Graphique obtenu pour $*s_2(t) = \sin (t+\pi)*$.
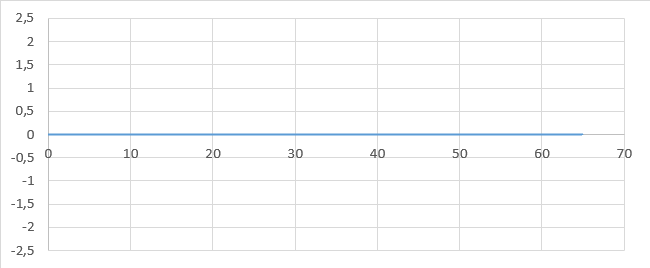
On constate que la valeur moyenne du carré de l’amplitude de la superposition est nulle, donc l’intensité de l’onde résultante est nulle. La superposition de deux ondes de même fréquence mais en opposition de phase a une intensité nulle.
Interférence de deux ondes
Maintenant, vous êtes en mesure de comprendre le petit paragraphe introductif de l’article de Wikipédia à propos des ondes…
Les interférences sont la combinaison de deux ondes susceptibles d'interagir. Ce phénomène apparaît souvent en optique avec les ondes lumineuses, mais il s’obtient également avec des ondes électromagnétiques d’autres longueurs d’onde, ou avec d’autres types d’ondes comme des ondes sonores. Le phénomène d'interférence [n’est observable que](…) lors de la combinaison de deux ondes de même fréquence.
Source : Wikipédia
Imaginons qu’on ait deux sources ponctuelles d’ondes lumineuses monochromatiques parfaitement synchrones (c’est-à-dire que les sources émettent de la lumière en phase). Je ne vous cache pas que dans la nature, ça n’arrive jamais 😊
Mais au labo, on a un moyen très simple de faire ça, j’en parlerai plus tard. Ça nous donne quelque chose qui est représenté sur l’animation ci-dessous.
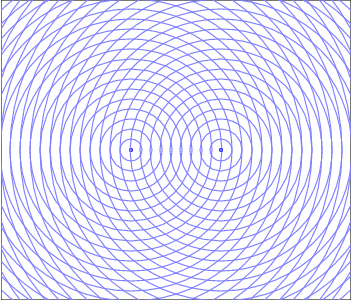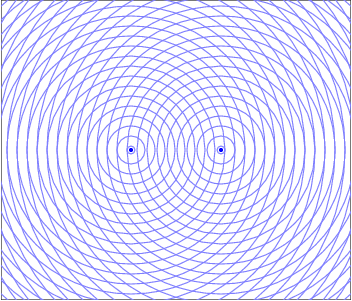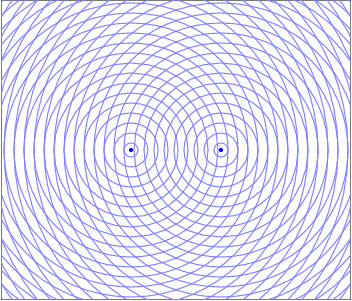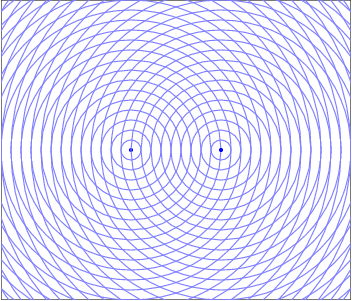
Prenons un point P au hasard dans l’espace autour des deux sources. Le chemin parcouru par l’onde issue de la source S1 et celui parcouru par l’onde issue de la source S2 n’a pas forcément la même longueur. Donc les deux ondes, bien que les sources émettent en phase, ne sont pas nécessairement en phase au niveau du point P.
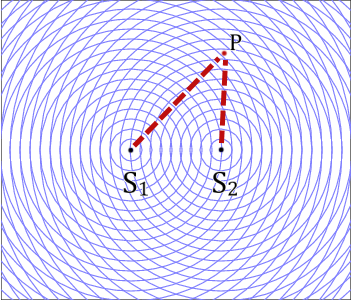
Mais il existe des endroits de l’espace où ces ondes sont en phase (et donc leur somme $*s_1(t) + s_2(t)*$ a une amplitude maximale). À ces endroits, il y a une interférence dite constructive car leurs amplitudes s’additionnent.
De même, il y a des endroits où ces deux ondes sont en opposition de phase. À ces endroits, on dit qu’il y a interférence destructive car les amplitudes se soustraient.
Toute l’astuce consiste à trouver où se trouvent ces endroits particuliers… 😊
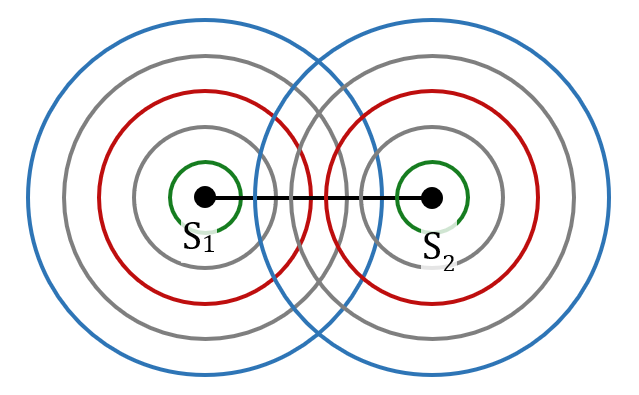
Sur cette figure, les cercles bleus correspondent à un « sommet » de l’onde (c’est-à-dire un maximum de la perturbation) émis au même moment par les deux sources S1 et S2. Idem pour les cercles rouges et les cercles verts. Les cercles gris correspondent à des minima.
Là où deux cercles colorés se rencontrent, il y a interférences constructives car les ondes sont en phase. Pareil là où les cercles gris se croisent.
Par contre, l’intersection d’un cercle gris avec un cercle coloré correspond à un maximum rencontrant un minimum. Les ondes sont, en ce point, en opposition de phase et il y a donc interférences destructives.
Interférence constructive
Dans l’exemple donné plus haut (les deux sources lumineuses synchrones), donner une position de P pour laquelle on aura une interférence constructive.
Correction
Si les ondes issues des deux sources parcourent le même chemin, alors elles arriveront en phase. Donc pour tous les points équidistants de S1 et S2, c’est-à-dire les points se trouvant sur la médiatrice du segment S1S2, il y aura interférence constructive.
Différence de chemin et décalage temporel
Si on sait évaluer la différence de chemin $*\mathrm{\delta}*$ que parcourent deux ondes issues de deux sources différentes pour arriver à un même point, alors on sait si elles interfèrent de manière constructive, destructive ou entre les deux.
L’onde qui parcourt le chemin le plus long arrive avec un certain retard, noté $*\tau*$ par rapport à l’onde qui a parcouru le chemin le plus court. Jusque là, vour devriez suivre sans difficulté… 😊
Si ce retard $*\tau*$ équivaut exactement à une période de l’onde, alors les deux ondes, qui étaient en phase au départ, seront aussi en phase à l’arrivé.
Eh bien parce que si ce retard correspond exactement à une période, alors lorsque le point P reçoit le sommet $*n*$ de l’onde qui a parcouru le plus court chemin, il reçoit en même temps le sommet $*n*$ – 1 de l’onde qui a parcouru le chemin le plus long. Il reçoit donc bien deux sommets en même temps, bien que ces sommets n’aient pas été générés en même temps.
Quelle est la différence de chemin qui génère un retard d’une période ? Eh bien une différence égale à la longueur d’onde de l’onde.

Et tout ce qu’on a dit pour un retard $*\tau*$ = $*T*$ et aussi vrai pour $*\tau*$ = 2$*T*$, 3$*T*$, … et donc pour $*\mathrm{\delta}*$ = $*\lambda*$, 2$*\lambda*$, 3$*\lambda*$ …
Par un raisonnement similaire, on montre qu’il y a interférence destructive si $*\tau*$ = 0,5$*T*$, 1,5$*T*$, 2,5$*T*$, … et donc pour $*\mathrm{\delta}*$ = 0,5$*\lambda*$, 1,5$*\lambda*$, 2,5$*\lambda*$ …
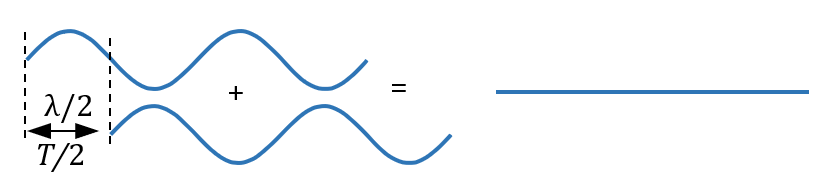
| Différence de chemin $*\mathrm{\delta}*$ | décalage temporel $*\tau*$ | Interférence |
|---|---|---|
| $*n\lambda*$ | $*nT*$ | constructive |
| ($*n*$ + 0,5)$*\lambda*$ | ($*n*$ + 0,5)$*T*$ | destructive |
Comment obtenir deux sources lumineuses synchrones au labo
On peut facilement observer des interférences lumineuses en faisant passant un faisceau laser à travers deux fentes (ou deux trous) proches. Chacune de ces fentes va se comporter comme une petite source lumineuse et les deux sources seront synchrones, c’est-à-dire en phase entre elle.
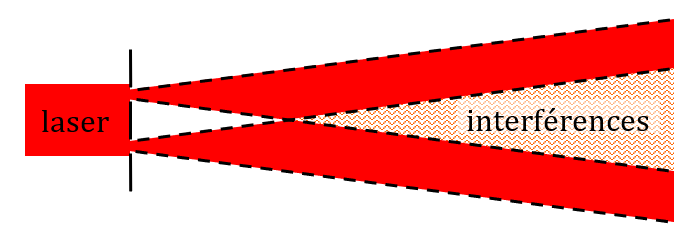
La fraction du faisceau laser qui passe par chaque trou est diffractée, comme on l’a vu dans la partie sur la diffraction. Chaque faisceau va donc s’ouvrir à cause du phénomène de diffraction, et dans une certaine zone de l’espace, ces deux faisceaux vont coexister. C’est dans cette zone qu’on pourra observer le phénomène d’interférence
Si la diffraction se fait par des fentes, on pourra observer, sur un écran placé devant les fentes (à une très grande distance devant l’écartement des fentes), la figure d’interférence suivante :

On reconnaît le motif de diffraction qu’on a déjà vu, mais celui-ci est découpé par une alternance des petites zones noires (où il y a interférence destructive) et de petites zones lumineuses (où il y a interférence constructive).
Expérience des fentes d’Young
Cette expérience est un classique en physique, pour des raisons que je n’ai pas le temps de développer ici. Le montage expérimental est celui décrit dans l’encadré « Comment obtenir deux sources lumineuses synchrones au labo ». Il permet de mettre en évidence des interférences lumineuses.
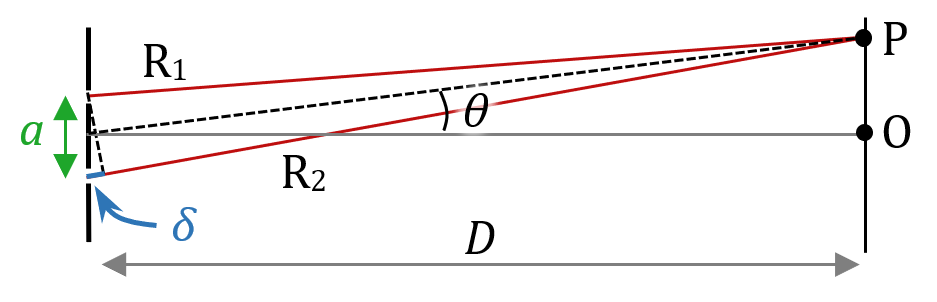
Le rayon R1 issu de la première fente parcourt une distance légèrement plus petite que le rayon R2 pour arriver jusqu’au point P. cette différence de marche, représentée en bleu et notée $*\mathrm{\delta}*$ est très petite devant la taille des rayons.
1. Exprimer $*\mathrm{\delta}*$ en fonction de $*\theta*$ et $*a*$. On considère que $*D*$ est tellement grand devant $*a*$ que les deux rayons R1 et R2 sont parallèles entre eux.
2. Que vaut $*\mathrm{\delta}*$ si le point P est situé en O ? Quel type d’interférence a-t-on en ce point ?
3. Établir l’expression littérale de la distance entre O et la première position de P pour laquelle on a de nouveau une interférence constructive. Comme $*\theta*$ est très petit, on a $* \sin \theta \simeq \tan \theta \simeq \theta*$.
Remarque : on appelle cette distance l’« interfrange ». C’est la distance qui sépare deux raies lumineuses consécutives. Si on peut mesurer cette distance expérimentalement, on peut en déduire la longueur d’onde de l’onde utilisée.
Correction
1. Refaisons le schéma pour y voir plus clair.
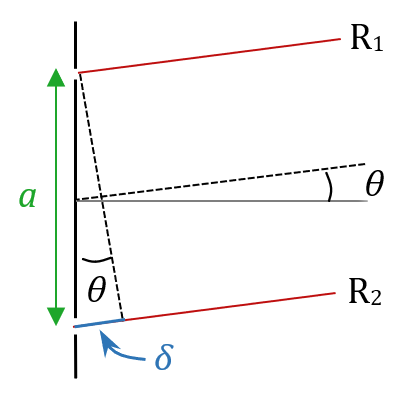
On voit que $*\sin \theta = \dfrac \delta a *$
Comme $*\theta*$ est très petit, on a $*\sin \theta \simeq \theta*$. Donc $*\delta \simeq a·\theta *$
2. Si le point P est situé en O, l’angle $*\theta*$ vaut 0, donc $*\delta*$ = 0. Les ondes arrivent sans décalage, donc elles sont en phase et donc il y a des interférences constructives.
3. Appelons $*i*$ cette distance. Comme il s’agit de la première position (c’est-à-dire la plus proche de O sans que ce soit O) où il y a des interférences constructives, ça veut dire que la différence de marche $*\delta*$ entre les ondes issues des deux sources est exactement égale à une longueur d’onde ($*\delta = \lambda*$).
D’autre part, $*i*$, $*D*$ et $*\theta*$ sont liés par la relation $µ\tan \theta = \dfrac iDµ$ (regardez sur le schéma de l’énoncé pour vous en convaincre).
Comme $*\theta*$ est tout petit, on a $*\theta \simeq \dfrac iD*$. Or $*\theta \simeq \dfrac \delta a = \dfrac \lambda a*$
Donc $µ i = \frac {\lambda D}a µ$
On remarque quelque chose de très intéressant : cette distance ne dépend pas de $*\theta*$ (tant que $*\theta*$ est petit et qu’on peut faire l’approximation $*\tan \theta \simeq \theta*$). Donc les raies lumineuses sont séparées par des intervales réguliers de largeur $*i*$. La mesure de cet intervale, qui peut être très précise (car cet intervale se répète), peut nous donner la valeur de la longueur d’onde de l’onde utiliser.
TP Interférence
- Exploiter l’expression donnée de l’interfrange dans le cas des interférences de deux ondes lumineuses, en utilisant éventuellement un logiciel de traitement d’image.
Objectif : déterminer la longueur d’onde d’un laser à partir d’une figure d’interférence.
Travail demandé
- Réaliser un montage permettant de recueillir une figure d’interférence formée par un laser passant à travers des fentes doubles. Vous mesurez avec précision la distance entre les fentes et l’écran.
- Prendre une photo de cette figure au verso de l’écran (qui est une simple feuille de papier – la figure est visible par transparence). Pour éviter toute déformation due à la perspective, vous placerez l’appareil photo bien dans l’axe du laser. Placez également un repère visible sur l’écran, de longueur précisémment connue.
Utilisez votre appareil en mode « pro » pour assombrir l’image. Attention : le repère de distance doit rester visible. Vous devez obtenir une figure ressemblant à celle-ci :
- Ouvrez cette photo avec Paint.net et utiliser ce logiciel pour déterminer le plus précisément possible la valeur de l’interfrange.
Déduire de vos mesures la longueur d’onde du laser utilisé.
Éléments de réponses
Effet Doppler
- Décrire et interpréter qualitativement les observations correspondant à une manifestation de l’effet Doppler.
- Établir l’expression du décalage Doppler dans le cas d’un observateur fixe, d’un émetteur mobile et dans une configuration à une dimension.
- Exploiter l’expression du décalage Doppler dans des situations variées utilisant des ondes acoustiques ou des ondes électromagnétiques.
Vous avez remarqué depuis votre plus tendre enfance que la fréquence du son émis par une sirène ou un moteur d’un véhicule est plus élevée quand le véhicule s’approche que quand le véhicule s’éloigne. D’accord, vous ne vous le formuliez pas comme ça… 😊
À que ce phénomène est-il dû ?
Mais non, mais non… Pas tant que ça. En fait, il n’y a aucun « phénomène physique » mytérieux et fascinant derrière l’effet Doppler. Tout s’explique de manière parfaitement logique !
Principe
Remarque : ce phénomène se manifeste pour toutes les ondes, y compris électromagnétique, bien que dans ce dernier cas, sa manifestation ne soit pas aussi « immédiate » que pour les ondes sonores. On en reparlera plus loin.
Émetteur immobile
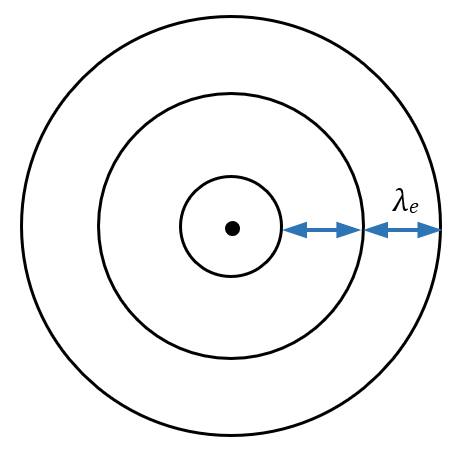
Si l’émetteur est immobile, la longueur d’onde $*\lambda_e*$ de l’onde qu’il émet dépend de la fréquence de l’onde $*f_e*$ et de sa vitesse $*c*$ dans le milieu de propagation. C’est la formule que vous connaissez depuis la 1e : $µ \lambda_e = \frac c{f_e}µ$
Émetteur en mouvement
Maintenant, imaginons une source d’onde en mouvement (disons vers la droite pour fixer les idées). À $*t*$ = 0, le signal émis par le source est à son maximum (on est au « sommet » d’une vague, qu’on va appelée vague n°1).
Pendant que la partie de l’onde qui se déplace vers la droite (dans le même sens que la source) avance, la source avance aussi.
Au bout d’un temps $*T_e*$ correspondant à une période de l’onde émise, le sommet n°1 a avancé d’une longueur $*\lambda_e = c·T_e*$.
Mais comme la source a également avancé dans cette direction, (disons d’une longueur $*d*$ < $*\lambda_e*$), le sommet n°2 ne sera pas émis à une distance $*\lambda_e*$ du sommet n°1, mais à une distance $*\lambda_e - d*$ plus petite.
La longueur d’onde de l’onde telle qu’elle est perçue par un récepteur fixe situé à droite de la source va être plus petite que si la source était immobile.
Et qui dit $*\lambda*$ plus petit dit $*f*$ plus grand. La fréquence perçue $*f_r*$ sera plus grande que la fréquence émise $*f_e*$.
Observez la figure ci-dessous.
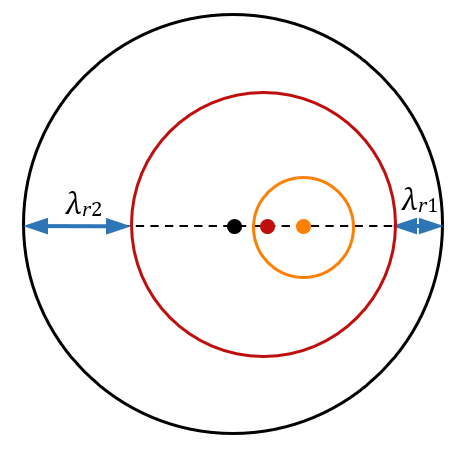
Lorsque la source se trouvait au niveau du point noir, elle a émis un maximum représenté en noir. Quelque temps plus tard, lorsqu’elle était dans la position en rouge, elle a émis un maximum représenté en rouge. Puis, lorsqu’elle était dans la position en orange, elle a émis le maximum en orange. Peu de temps après, on a pris une « photo » correspondant à la figure représentée.
À cause du déplacement de la source, l’onde émise « vers l’avant » a une longueur d’onde plus courte. Sa longueur d’onde perçue $*\lambda_{r1}*$ pour un récepteur qui se situerait devant la source est égale à la longueur d’onde de l’onde émise $*\lambda_e*$ si la source était immobile, moins la distance parcourue par la source pendant une période ($*vT*$). La longueur d’onde perçue est donc plus courte que la longueur d’onde émise, et donc la fréquence perçue est plus élevée. Le son est plus aigu. Il est d’autant plus aigu que la source est rapide.
L’onde émise vers l’arrière voit sa longueur d’onde augmenter pour les mêmes raisons et $*\lambda_{r2} = \lambda_e + vT*$.
À toute allure
Vous êtes sur le bord de la route lorsque une moto s’approche de vous à toute allure. Lancée à 280 km·h-1, son moteur tourne à 12.000 tour·min-1. 🏍
Sachant que la fréquence du son émis par le moteur est égale à la fréquence de rotation de celui-ci, déterminer :
1. La fréquence du son perçue lorsque la moto s’approche
2. La fréquence du son perçue lorsque la moto s’éloigne.
Correction
1. Fréquence $*f_e*$ du son émis par le moteur : 12000÷60 = 200 Hz.
Longeur d’onde du son émis par le moteur : $*\lambda_e*$ = 340÷200 = 1,70 m.
Période du son émis : 1÷200 = 5,00 ms.
Pendant une période (soit 5,00 ms), la moto parcourt 280÷3,6×5·10-3 = 0,389 m
Donc la longueur d’onde perçue $*\lambda_r*$ = 1,70 – 0,389 = 1,31 m.
La fréquence perçue $*f_r*$ vaut $*f_r = \frac c{\lambda_r} =*$ 260 Hz
2. Par un raisonnement analogue, on détermine que $*\lambda_r*$ = 2,09 m
Et donc que $*f_r*$ = 163 Hz
Décalage Doppler et vitesse
Le but de ce paragraphe et de vous faire trouver le lien mathématique entre la vitesse de la source par rapport à l’émetteur et le décalage Doppler, c’est-à-dire la différence entre la fréquence émise par la source et la fréquence perçue par le récepteur.
Mais tout d’abord, une petite précision. Rappelez-vous ce que je vous disais en début de paragraphe à propos de l’effet Doppler :
Pourquoi ai-je mis peut en gras ? Eh bien parce que ce n’est pas toujours le cas. Pour que ce soit le cas, il faut que la distance émetteur – récepteur varie.
Non, pas forcément… Pensez à la Terre qui tourne autour du Soleil.
Donc, pour qu’il y ait effet Doppler, il faut que la source s’approche ou s’éloigne du récepteur.
On va toujours se placer dans le cas le plus simple où la source se déplace sur une droite sur laquelle se trouve également le récepteur.
Non, on ne va pas se poser le problème du croisement de la source et du récepteur. C’est une modélisation simple… ne cherchez pas la petite 🐞.
D’ailleurs, c’est tellement simple que vous allez chercher cette relation vous-même. Allez hop ! Exercice.
Vitesse et décalage Doppler
On considère une source d’onde (lumineuse ou sonore, on s’en fiche pour l’instant) se déplaçant le long d’une droite (AB) à une vitesse $*v*$.
L’onde émise se déplace avec une vitesse $*c*$. La fréquence de l’onde émise est notée $*f_e*$.
Un récepteur se trouve sur cette droite. La fréquence de l’onde reçue est notée $*f_r*$.
Question : donner la relation liant $*f_r*$, $*f_e*$, $*v*$ et $*c*$ en distinguant le cas où l’émetteur s’éloigne de la source et le cas où il se rapproche.
Remarque : on suppose que l’émetteur s’approche où s’éloigne de la source à une vitesse inférieure à la vitesse de propagation de l’onde. Ça va sans dire s’il s’agit d’onde lumineuse, mais ce n’est pas une obligation dans le cas d’une onde sonore.
Correction
Pendant que l’onde parcourt un distance $*\lambda_e*$, la source parcourt une distance $*vT*$.
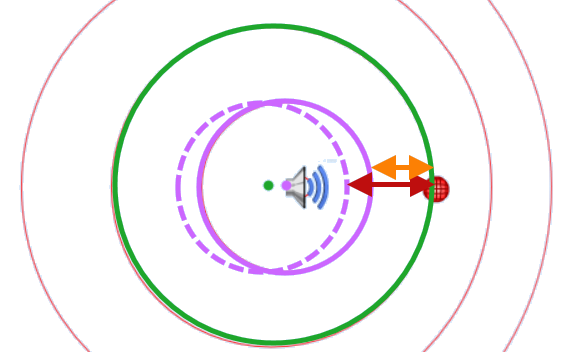
Dans le cas où l’émetteur se rapproche du récepteur, le deuxième sommet (cercle continu violet) n’est pas émis à une distance $*\lambda_e*$ du premier (cercle vert), mais à une distance plus courte $*\lambda_r = \lambda_e - vT*$.
Sur la figure, le cercle violet en pointillé représente le deuxième sommet si l’émetteur n’avait pas bougé.
De la même manière, si on se place l’émetteur s’éloigne du récepteur, on a $*\lambda_r = \lambda_e + vT*$
Plutôt que de retenir deux formules, on adopte la convention suivante :
• Si le l’émetteur se rapproche du récepteur, $*v*$ > 0.
• Dans le cas contraire, $*v*$ < 0.
Ceci permet de n’avoir qu’une seule formule à retenir : $*\lambda_r = \lambda_e - vT*$.
L’énoncé demande de donner la relation liant $*f_r*$, $*f_e*$, $*v*$ et $*c*$. Il faut donc se servir du fait que $*\lambda = \frac cf*$.
On obtient alors :
$µ f_r = \dfrac 1{1-\frac vc}f_e µ$
| $* f_r = \dfrac 1{1-\frac vc}f_e *$ |
$*f_r*$ : fréquence reçue $*f_e*$ : fréquence émise $*v*$ : vitesse de rapprochement (>0) ou d’éloignement (<0) de l’émetteur $*c*$ : vitesse (ou célérité) de l’onde |
✋ Il faut savoir retrouver cette formule.
Mesure d’une vitesse par effet Doppler
- Exploiter l’expression du décalage Doppler en acoustique pour déterminer une vitesse.
Fichiers à télécharger
Enregistrement sonore et Vidéo à exploiter
Travail demandé
- À l’aide d’Audacity, déterminer la fréquence du son avant et après passage du vélo. En déduire la vitesse du vélo.
- Estimer l’incertitude portant sur la valeur de la vitesse.
- Vérifier la valeur trouvée par pointage du fichier vidéo sur Regressi. Ces deux valeurs de vitesse sont-elles compatibles ?
Éléments de réponses
1. Détermination de la vitesse du vélo par effet Doppler
On a, dans cette situation, deux inconnues : la fréquence émise par le haut-parleur et la vitesse du vélo. Mais on peut obtenir deux équations : la fréquence reçue $*f_{r1}*$ avant le passage du vélo et celle reçue après son passage $*f_{r2}*$. On obtient donc un système d’équations qui nous permettent de trouver la vitesse du vélo. $µ \left\{ \begin{aligned} f_{r1} =& \dfrac 1{1-\frac vc}f_e \\ f_{r2} =& \dfrac 1{1+\frac vc}f_e \end{aligned} \right. µ$
En utilisant l’analyse spectrale d’Audacity, on trouve que la fréquence avant le passage du vélo vaut $*f_{r1}*$ = 1216 Hz, et après le passage $*f_{r2}*$ = 1185 Hz.
On isole $*v*$ et on note $*\alpha*$ le rapport $*\frac {f_{r1}}{f_{r2}}*$. On obtient la relation : $µ v = \frac {\alpha -1}{\alpha +1}c µ$
En prenant comme vitesse du son dans l’air $*c*$ = 340 m·s-1, on calcule que $*v*$ ≃ 4,4 m·s-1.
2. Estimation de l’incertitude sur cette vitesse
Audacity arrondi à l’hertz près la fréquence mesurée. C’est l’erreur minimale portant sur cette mesure. On a donc $*f_{r1}*$ = 1216 Hz ± 0,5 Hz et $*f_{r2}*$ = 1185 Hz ± 0,5 Hz
Cette incertitude permet de calculer l’incertitude portant sur $*\alpha*$ : en prenant les valeurs extrêmes possibles pour $*\alpha*$, on trouve que $*\alpha*$ = 1,026 ± 0,001.
On peut ensuite calculer les valeurs extrêmes de $*v*$ : entre 4,25 et 4,53 m·s-1, que l’on peut écrire (4,4 ± 0,2) m·s-1.
3. Détermination de la vitesse par pointage vidéo
Après pointage vidéo et modélisation de la trajectoire, on trouve que $*v*$ = 4,25 m·s-1. En considérant une erreur de 5 % sur l’étalonnage en distance de la vidéo, on a $*v*$ = (4,25 ± 0,20) m·s-1. On voit que ces deux mesures sont compatibles entre elles : l’intersection des valeurs possibles pour chaque méthode n’est pas nulle.
Révision & entraînement
Interféromètre de Michelson
Cet exercice a été donné en devoir en 2020/2021
La détection des ondes gravitationnelles, réalisées pour la première fois en 2015, nécessite de mesurer des variations de longueur extrêmement petites (de l’ordre d’un millième de la taille d’un proton sur plusieurs kilomètres, soit une variation relative de 10-21 !). Cette détection est rendue possible par un interféromètre de Michelson géant. Cet exercice se propose d’étudier comment on peut, grâce à cet appareil, détecter de faible variation de longueur.
Le principe de l’interféromètre de Michelson est le suivant.
Un faisceau de lumière issu d’une source laser est séparé en deux au point A d’une lame séparatrice semi-réfléchissante. Chacun des deux faisceaux ainsi formés est alors en phase. Ils constituent un système de sources cohérentes.
Ces deux faisceaux sont réfléchis par les miroirs plans M1 et M2 (respectivement aux point B et C) et redirigés vers le point A de la lame séparatrice pour finalement se rejoindre au niveau d’un capteur qui mesure l’intensité lumineuse résultante.
L’un des miroirs (le miroir M1 par exemple) peut être déplacé avec une grande précision.
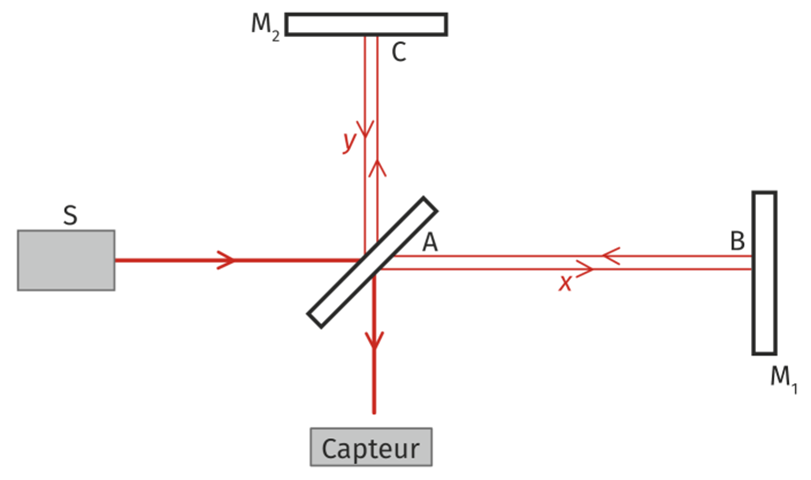
1. Lorsque les deux miroirs sont à la même distance de la lame semi-réfléchissante ($*x*$ = $*y*$), comment les rayons arrivent-ils au niveau du capteur (en phase ou en opposition de phase) ? Justifier.
2. Si M1 avance d’une longueur $*\delta x*$, quelle est la différence de marche entre les deux rayons ?
3. À quelle condition cette différence de marche va-t-elle créer une interférence destructive ?
On considère que la variation minimale de longueur de $*x*$ est celle qui va faire passer les interférences de constructives à destructives ou inversement.
4. Exprimer la plus petite variation de longueur de $*x*$ détectable en fonction de la longueur d’onde du laser utilisé.
5. Si on utilise un laser d’une longeur d’onde de 400 nm et que la distance $*x*$ vaut 1,00 m, quelle est la précision de la mesure (exprimée par $* \frac {\delta x}x*$) ? Exprimer également cette précision en pourcentage.
Correction
1. En phase, car ils sont en phase au départ et ils parcourent la même distance.
2. La différence de marche est de $*2 \delta x*$ (à cause de l’aller-retour).
3. Si cette différence de marche est égale à $*n*$+0,5 fois la longueur d’onde, avec $*n*$ entier relatif.
4. La plus petite variation $*\delta x*$ est celle qui va causer une différence de marche de 0,5$*\lambda*$. Donc $*2 \delta x*$ = $*0,5 \lambda *$ et donc $* \delta x*$ = $*0,25 \lambda*$.
5. $* \delta x*$ = 100 nm, donc $*\frac{ \delta x}x*$ = 10-7, soit 10-5 %.
Effet doppler et astrophysique
Cet exercice est extrait de l’épreuve de bac Polynésie 2013
L’effet Doppler constitue un moyen d’investigation utilisé en astrophysique.
Cet exercice s’intéresse à deux applications distinctes : l’étude de l’expansion de l’Univers en expansion et la détection d’une étoile double « spectroscopique ».
Donnée : 1 Å = 0,1 nm
Document 1. Principe de l’effet Doppler
On note $*λ_0*$ la longueur d’onde de référence de la raie étudiée dans le spectre (source immobile par rapport à l’observateur) et $*λ*$ la longueur d’onde de la radiation émise par la source en mouvement.
Lorsqu’une étoile s’éloigne de la Terre, on observe un décalage vers les grandes longueurs d’onde appelé « redshift » et caractérisé par le nombre : $µ z = \frac {\lambda - \lambda _0}{\lambda _0} µ$
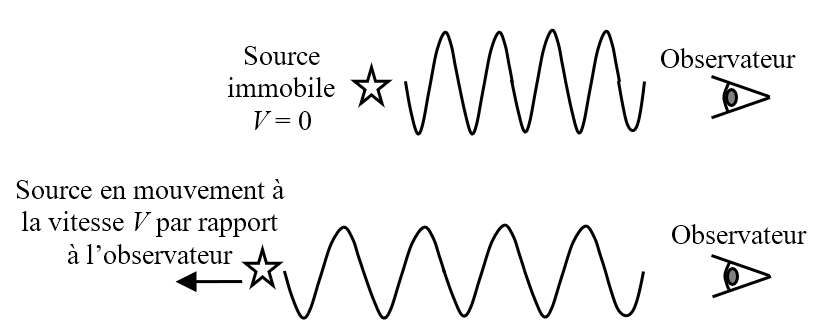
La formule de Doppler donne la vitesse d’éloignement $*v*$ de la source lumineuse par rapport à l’observateur terrestre dans le cas non relativiste : $µ v = c \frac {λ-λ_0}{λ_0} µ$ $*c*$ est la célérité de la lumière dans le vide ($*c*$ = 3,00·108 m·s-1).
Document 2. Décalage vers le rouge
En 1930, Edwin HUBBLE avait constaté expérimentalement que plus les galaxies étaient lointaines, plus leur spectre présentait un décalage vers le rouge important.
Le « décalage vers le rouge », qui sera appelé « redshift » apparaît, quand il est petit, comme proportionnel à la distance : $µ z = \frac {H_0⋅d}c µ$ où $*H_0*$ est une constante appelée constante de Hubble.
Ce décalage est traditionnellement interprété comme dû à la vitesse d’éloignement des galaxies. Cette interprétation, si elle est vraie pour les « redshifts » petits, est en fait fondamentalement erronée dans une perspective de relativité générale. Les « redshifts » observés vont d’une fraction de l’unité pour la plupart des galaxies, à 4 ou 5 pour les objets les plus lointains, quasars, ou certaines autres galaxies.

1. Preuve de l’expansion de l’Univers
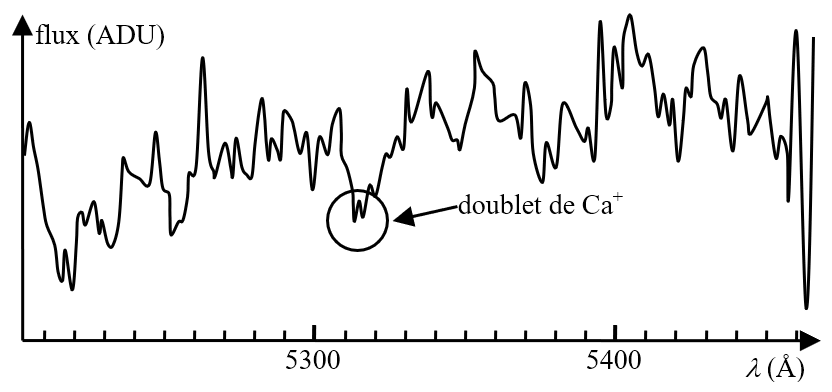
1.1. En utilisant le document 3, déterminer la longueur d’onde médiane du doublet de $*\ce{Ca+}*$ dans le spectre de la galaxie nommée NGC 691.
Sachant que la longueur d’onde médiane $*λ_0*$ de ce doublet mesurée sur Terre pour une source au repos est de 5268 Å, calculer le « redshift » $*z*$ caractérisant le décalage vers le rouge de cette galaxie.
1.2. Calculer la vitesse d’éloignement de la galaxie NGC 691 par rapport à la Terre.
1.3. À l’aide des documents 1 et 2, établir dans le cas non relativiste, la relation entre la vitesse d’éloignement $*v*$ de la galaxie et sa distance $*d*$ à la Terre, montrant que $*v*$ est proportionnelle à $*d*$.
1.4. À partir des valeurs du nombre $*z*$ données dans le document 2, montrer que l’expression utilisée pour calculer la vitesse d’éloignement des galaxies donnée dans le document 1 n’est pas applicable dans tous les cas.
2. Détection d’une étoile double « spectroscopique »
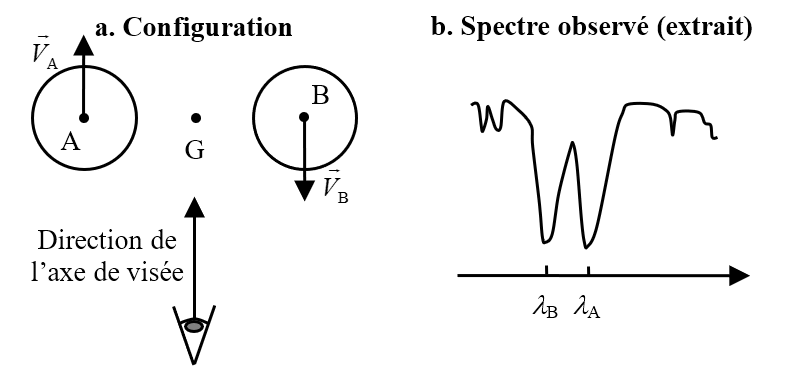
On appelle « étoile double » un système stellaire composé de deux étoiles proches en orbite autour du même point (ce point étant le centre d’inertie G du système).
Une étoile double « spectroscopique » est constituée de deux astres trop proches pour être séparés par un télescope optique et ne peut être détectée que par l’étude de son spectre à haute résolution. Le mouvement des deux étoiles provoque en effet un léger déplacement des raies d’absorption du spectre par effet Doppler.
Dans les questions suivantes, on suppose que les deux étoiles A et B décrivent des orbites circulaires de même rayon $*R*$, avec la même valeur de vitesse $*v*$ = $*v_A*$ = $*v_B*$.
La période de rotation commune aux deux étoiles A et B est notée $*T*$. C’est la période de l’étoile double.
2.1. Expliquer pourquoi, dans la situation décrite sur le document 4, on a $*λ_A*$ > $*λ_B*$.
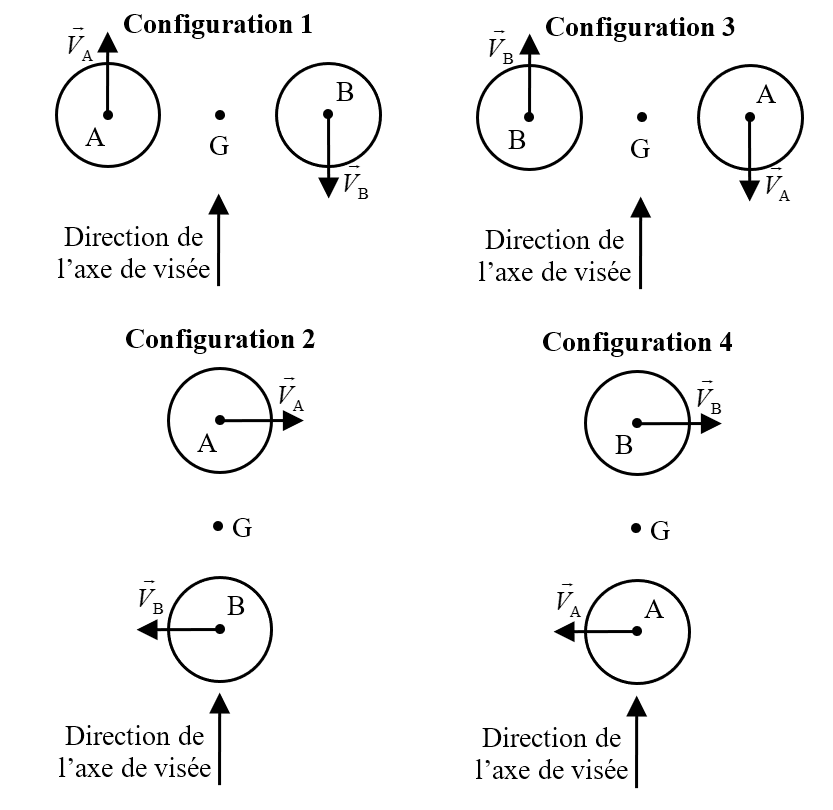
2.2. Sachant que l’effet Doppler ne se manifeste pas lorsque le vecteur vitesse de la source est perpendiculaire à la direction de visée, compléter en justifiant le tableau ci-dessous. Schématiser sans souci d’échelle le spectre correspondant à chaque configuration et montrer que l’évolution temporelle de ces spectres est périodique, de période $*T*$/2.
| Relation entre $*\lambda_A*$ et $*\lambda_B*$ | $*\lambda_A*$ = $*\lambda_B*$ | $*\lambda_A*$ > $*\lambda_B*$ | $*\lambda_A*$ < $*\lambda_B*$ |
|---|---|---|---|
| Configuration(s) |
2.3. En utilisant les spectres du document 5 qui montrent l’évolution temporelle de la position de la raie Hα dans le spectre de l’étoile double HD 80715, vérifier que la période $*T*$ de celle-ci est voisine de 3,8 jours.
Correction
1.1. Valeur médiane de $*\lambda*$ dans le spectre de NGC 691 : environ 5315 Å.
$*z*$ = (5315-5268)÷5268 = 8,922·10-3
1.2. $*v*$ = $*c·z*$ = 2,67·106 m·s-1
1.3. $*v*$ = $*c·z*$ et $*z*$ = $*H_0·\frac dc*$, donc $*v*$ = $*H_0·d*$. $*v*$ est bien proportionnel à $*d*$.
1.4. Le doc. 1 dit que $*v*$ = $*c·z*$. Or si $*z*$ est égal à 4 ou 5, on obtient une vitesse d’éloignement 4 ou 5 fois supérieure à la vitesse de la lumière, ce qui n’est pas possible.
2.1. L’étoile A s’éloigne de l’observateur, ce qui va augmenter les longueurs d’onde de ses rayonnements, par effet Doppler. L’étoile B se rapproche de l’observateur, ce qui va diminuer les longueurs d’onde des rayonnements émis. D’où $*\lambda_A*$ > $*\lambda_B*$.
2.2. On a $*\lambda_A*$ = $*\lambda_B*$ lorsque les étoiles se déplacent perpendiculairement à l’axe de visée (cas 2 et 4). $*\lambda_A*$ > $*\lambda_B*$ pour le cas 1 (justification dans la réponse précédente). Par le même raisonnement, on montre que $*\lambda_A*$ < $*\lambda_B*$ pour le cas 3.
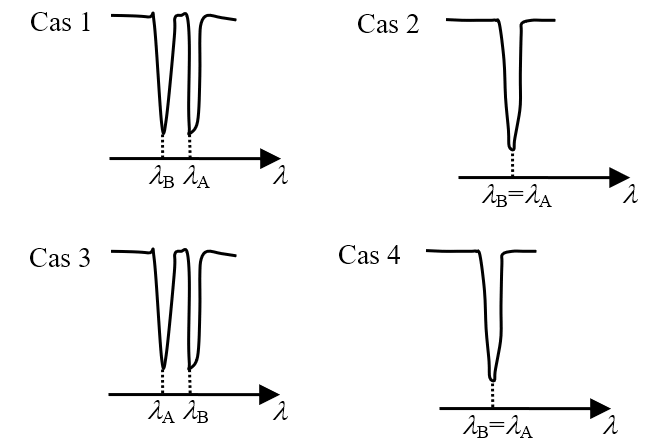
On constate que lors d’une révolution complète des 2 étoiles, la superposition des raies arrivent 2 fois (cas 2 et 4) et leurs écartement maximum également (cas 1 et 3). La périodicité de l’évolution du spectre est donc 2 fois plus courte que celle de la révolution des étoiles.
2.3. Les 2 raies coïncident pour $*t*$ = 0,061 jour puis quelque part entre 1,886 et 2,038 jours soit une date moyenne de 1,962. Cela fait une période de 1,962 – 0,061 = 1,901 jour. La période de rotation de cette étoile double est d’environ 1,9×2 = 3,8 jours.