Physique & Chimie au lycée

Cours de physique-chimie pour les classes de 1ère et Terminale

Sommaire
SP-1 ES-1
SP-T ES-T
3e SNT
Divers Annales
Contact

P9. Radioactivité

Certains noyaux atomiques sont instables du fait de leur ratio protons/neutrons ou du grand nombre de nucléons qu’ils contiennent. Ils se transforment au bout d’un temps aléatoire en d’autres noyaux après émission de particules.

Désintégration radioactive
  • Déterminer, à partir d’un diagramme (N,Z), les isotopes radioactifs d’un élément.
  • Utiliser des données et les lois de conservation pour écrire l’équation d’une réaction nucléaire et identifier le type de radioactivité.

Noyaux radioactifs

Les 118 éléments connus à ce jour ont tous plusieurs isotopes, dont certains (voire tous) sont instables. Un noyau instable est dit « radioactif » car, au bout d’un temps aléatoire, il se « désintègre » spontanément.

Diagramme de Segrè interactif

Le terme « désintégrer », bien qu’il soit fréquemment utilisé, peut prêter à confusion… En fait, le noyau ne disparaît pas, il émet une petite particule et peut éventuellement se transformer en un autre noyau.

Exemple de l’uranium 238 ($*\ce{^{238}U}*$)

L’uranium 238 est l’isotope de l’uranium le plus courant sur Terre (99,3 %). Son noyau possède 92 protons et 146 neutrons.
Un noyau d’uranium 238 donné à une probabilité de 50 % de se désintégrer au cours d’une période de 4,5 milliards d’année.
En se désintégrant, il éjecte une particule α de son noyau, c’est-à-dire un noyau d’hélium 4 ($*\ce{{^4_2}He}*$).
Après cette désintégration, il restera toujours un noyau, mais celui-ci aura 90 protons et 144 neutrons : il s’agit du thorium 234 ($*\ce{^{234}_{90}Th}*$)

Lois de conservation

Au cours d’une transformation nucléaire, il y a conservation du nombre de nucléons et des charges.

Différentes radioactivités

Radioactivité α

Elle concerne les noyaux très lourds. Lors d’une désintégration α, le noyau « père » émet une particule α c’est-à-dire un noyau de $*\ce{{^4_2}He}*$ composé de deux protons et de deux neutrons.

Le noyau « fils » aura donc deux protons et deux neutrons en moins par rapport au noyau père.

Radioactivité β+ et β–

La radioactivité β– correspond à une désintégration par émission d’un électron (et d’un antineutrino – particule très légère et neutre).
Cette désintégration concerne les noyaux ayant un excès de neutrons par rapport à leur proton. Elle correspond en fait à la transformation d’un neutron en proton à l’intérieur d’un noyau, avec émission d’un électron pour la conservation de la charge.

La radioactivité β+ est l’émission d’un antiélectron (un positon ou positron) et d’un neutrino, lors de la transformation d’un proton en neutron. Elle concerne les noyaux ayant un excès de protons.

Radioactivité γ

Tout comme un atome peut être dans un état excité et émettre de l’énergie sous forme d’un photon afin d’atteindre un état plus stable, un noyau obtenu après désintégration α ou β se trouve généralement dans un état excité.
Il va donc se désexciter en émettant un photon. Ce photon (qualifié de photon γ) aura une très grande énergie (et sera donc associé à un rayonnement de très courte longueur d’onde).

On marque généralement d’une astérisque un noyau se trouvant dans un état excité : $µ \ce{^A_ZX^* \rightarrow {^A_Z}X + \gamma} µ$

Désintégrations radioactives

Compléter les équations suivantes en précisant la particule p et le noyau fils $*\ce{{^A_Z}X}*$

1. (β+)   $*\ce{^{15}_8O \rightarrow {^A_Z}X + p} *$

2. (β–)   $*\ce{{^3_1}H \rightarrow {^A_Z}X + p} *$

3. (γ)   $*\ce{^{234}_{91}Pa^* \rightarrow {^A_Z}X + p} *$

4. (α)   $*\ce{^{212}_{84}Po \rightarrow {^A_Z}X + p} *$

5. (β–)   $*\ce{^{14}_6C \rightarrow {^A_Z}X + p} *$

6. (α)   $*\ce{^{172}_{79}Au \rightarrow {^A_Z}X + p} *$

Correction

Je précise le contenu des électrons et positrons, pour faciliter la visualisation de la conservation des charges et des nucléons. Mais ce n’est pas une obligation.

1. (β+)   $*\ce{^{15}_8O \rightarrow {}^{15}_7N + {^0_1}e^+} *$

2. (β–)   $*\ce{{^3_1}H \rightarrow {^3_2}He + {^0_{-1}}e^-} *$

3. (γ)   $*\ce{^{234}_{91}Pa^* \rightarrow {}^{234}_{91}Pa + \gamma} *$

4. (α)   $*\ce{^{212}_{84}Po \rightarrow {}^{208}_{82}Pb + {^4_2}He} *$

5. (β–)   $*\ce{^{14}_6C \rightarrow {}^{14}_7N + {^0_{-1}}e^-} *$

6. (α)   $*\ce{^{172}_{79}Au \rightarrow {}^{168}_{77}Ir + {^4_2}He} *$

Loi de décroissance radioactive
  • Établir l’expression de l’évolution temporelle de la population de noyaux radioactifs.
  • Exploiter la loi et une courbe de décroissance radioactive.
  • Capacité mathématique : résoudre une équation différentielle linéaire du premier ordre à coefficients constants.

À l’échelle des noyaux, il faut savoir qu’un type de noyau radioactif donné (par exemple un noyau de $*\ce{^{238}U}*$), a une certaine probabilité de se désintégrer chaque seconde.
Cette probabilité dépend uniquement de la constitution du noyau. Tous les noyaux de $*\ce{^{238}U}*$ par exemple, ont la même probabilité de se désintégrer chaque seconde. Cette probabilité n’est pas la même si on considère un noyau de $*\ce{^{235}U}*$ ou de $*\ce{^{14}C}*$.

Cette propriété rend donc possible d’élaborer une loi qui va décrire l’évolution d’un grand nombre de noyaux. Souvenez-vous, on a déjà vu ça l’année dernière en Enseignement scientifique (chap. 1.1 Éléments chimiques & radioactivité).

Activité : loi de décroissance

Imaginons un échantillon de $*N_0*$ noyaux radioactifs identiques ($*N_0*$ est très grand), dont la probabilité de se désintégrer chaque seconde est de $*\lambda*$.

1. En utilisant la loi des grands nombres, prévoir le nombre de désintégrations $*x*$ ayant lieu dans l’échantillon durant un temps $*\Delta t*$ suffisamment petit pourqu’on puisse considérer la variation de $*N*$ négligeable durant cette période.

En mathématiques, la loi des grands nombres permet d’interpréter la probabilité comme une fréquence de réalisation et présente l’espérance comme une moyenne.

2. Si on fait tendre $*\Delta t*$ vers 0, montrer que $µ -\frac{\mathrm{d}N}{\mathrm{d}t} = \lambda N µ$

3. Donner l’expression de la quantité $*N(t)*$ de noyaux non encore désintégrés dans l’échantillon en fonction du temps.

L’activité $*A*$ d’un échantillon de matière radioactive est le nombre de désintégrations qui a lieu dans cet échantillon chaque seconde.

4. Trouver l’expression de $*A*$ en fonction de $*N*$ de notre échantillon.

Vous venez d’établir la loi de décroissance radioactive. 😎

Activité radioactive

L’activité $*A*$ d’un échantillon radioactif, c’est le nombre de désintégrations qui s’y déroulent chaque seconde.
L’unité de l’activité est le bequerel (Bq), qui correspond en fait à des s-1.

Exemples d’activités

1 L d’eau douce : 1 Bq
1 kg de légume : 150 Bq
Humain (70 kg) : 8000 Bq

Cette activité est proportionnelle à la quantité $*N*$ de noyaux radioactifs présents dans l’échantillon. S’il n’existe qu’un seul type de noyaux radioactifs dans l’échantillon, et que leur probabilité de se désintégrer chaque seconde vaut $*\lambda*$, on a :

$µ A = \lambda N µ$

Loi de décroissance radioactive

Pendant une durée infinitésimale $*\mathrm{d}t*$, il y a un certain nombre infinitésimal $* \lambda N \mathrm{d}t *$ de noyaux qui se désintègrent.
Donc la quantité de noyaux $*N*$ varie d’un nombre $*\mathrm{d}N*$ < 0 (car $*N*$ diminue) tel que : $µ \mathrm{d}N = - \lambda N \mathrm{d}t µ$

Et hop ! Équation différentielle 😁

$µ \frac {\mathrm{d}N}{\mathrm{d}t} = - \lambda N µ$

Vous savez que cette équation différentielle a pour solution :

$* N(t) = N_0·e^{-\lambda t} *$ $*N(t)*$ : nombre de noyaux restant à un temps $*t*$
$*N_0*$ : nombre de noyaux à $*t*$ = 0
$*\lambda*$ : probabilité qu’un noyau se désintègre chaque seconde.

$*N(t)*$ suit donc une évolution en exponentielle décroissant que vous connaissez bien (transfert thermique, décharge d’un condensateur, cinétique d’ordre 1…).

Allure de $*N(t)*$

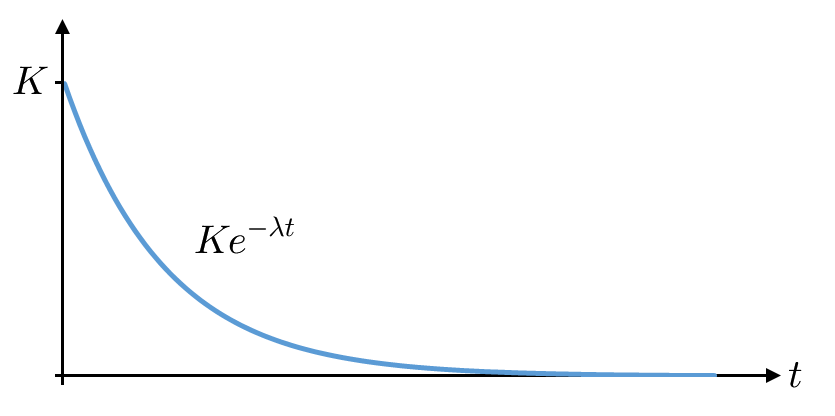
Du coup, comme $*A = \lambda N*$, on a également $*A*$ = $*\lambda N_0·e^{-\lambda t}*$, d’où :

$µ A = A_0·e^{-\lambda t} µ$

Cette expression est appelée « loi de décroissance radioactive »

Demi-vie

Plutôt que la constante $*\lambda*$, les tables de données mentionnent la « demi-vie » d’un isotope radioactif, notée $*t_{1/2}*$. C’est le temps au bout duquel un noyau de cet isotope a 50 % de chance de se désintégrer.
Ou bien, si on raisonne sur un échantillon macroscopique, c’est le temps au bout duquel la quantité de noyaux radioactifs de cet isotope a été divisée par deux.

$µ \lambda = \frac {\ln 2}{t_{1/2}} µ$

Demi-vie

1. Démontrer la relation $* \lambda = \dfrac {\ln 2}{t_{1/2}} *$

2. La demi-vie du $*\ce{^{14}C}*$ est de 5730 ans. Quelle est la probabilité qu’un tel noyau se désintègre chaque seconde ?

Datation
  • Expliquer le principe de la datation à l’aide de noyaux radioactifs et dater un évènement.

La radioactivité est un phénomène naturel omniprésent. Cette activité est aussi présente dans les roches et dans les organismes. Lorsque ceux-ci ne renouvellent plus la quantité d’isotopes par des échanges avec l’extérieur, l’activité radioactive décroît. Si la population initiale $*N_0*$​ en noyaux radioactifs est connue, une mesure de $*A*$ à un instant $*t*$ peut permettre une datation.

Pour choisir un isotope radioactif lors d’une datation, il faut que :

  • l’isotope soit présent initialement dans l’organisme ou l’objet à dater ;
  • le temps de demi-vie $*t_{1/2}*$​ de l’isotope ne soit pas trop court par rapport à l’âge de l’échantillon analysé.

Le mieux est de traiter un cas concret sous forme d’exercice

Datation au carbone 14

Les réactions nucléaires ayant lieu dans la haute atmosphère entraînent une teneur constante de l’atmosphère en $*\ce{^{14}C}*$ (et de tout les corps échangeant du carbone avec l’atmosphère). En effet, celui-ci se désintègre naturellement à un rythme identique à celui de sa formation.

Un atome de carbone de l’amosphère sur 1012 est un atome de $*\ce{^{14}C}*$.

Le bois sec contient 50 % de carbone en masse. Le reste étant principalement de l’oxygène et de l’hydrogène.

1. Calculer l’activité de 100 g de bois sec récent (c’est-à-dire pour lequel on peut négliger la diminution de la part de $*\ce{^{14}C}*$ due à la décroissance radioactive).

2. On mesure l’activité de bois récupéré sur l’épave d’un navire. Cette activité, pour 100 g de bois sec, vaut $*A*$ = (7,6 ± 0,1) Bq. Donner une estimation de l’âge de ce bois. Est-on sûr qu’il s’agit de l’âge du navire ?

Article Wikipédia sur la datation au carbone 14, mentionnant notamment ses limites et corrections.

Radioactivité & santé
  • Citer quelques applications de la radioactivité dans le domaine médical.
  • Citer des méthodes de protection contre les rayonnements ionisants et des facteurs d’influence de ces protections.

La radioactivité est utilisée dans de nombreuses applications médicales (imagerie, radiothérapie pour détruire des cellules cancéreuses).

Une exposition excessive (ponctuelle ou permanente), peut avoir des conséquences sur la santé.

Les méthodes de protection dépendent du type de radioactivités et de la durée d’exposition.

  • Les particules α sont facilement arrêtées (une feuille de papier suffit).
  • Pour se protéger du rayonnement β, une feuille d’aluminium de quelques millimètres suffit. On peut également utiliser une feuille de verre ou un écran d'un centimètre de plexiglas, qui permet d’arrêter une majorité de ces particules.
  • Le rayonnement γ va pénétrer davantage dans l’organisme que les rayonnements α et β, mais il modifie moins les particules qu’il rencontre. On s’en protège par un blindage très épais. Par exemple, pour réduire de seulement 30 % ce rayonnement, il est nécessaire d’être derrière 6 cm de plomb, 30 cm de béton ou 54 cm de terre.

Révision & entraînement

Datation des roches par le potassium 40

Le potassium 40 $*\ce{_19^40K}*$ est un isotope radioactif du potassium, qui se désintègre par émission β+ avec une demi-vie de 1,25 milliard d’années.

Il est utilisé pour daté les roches magmatiques, de la façon suivante :

  • On suppose que le magma au départ ne contenait pas d’argon (l’argon est un gaz noble – donc non réactif. Au moment de l’éruption volcanique, ce gaz, s’il était présent, s’échappe du magma). Il contient, par contre, du potassium, y compris du potassium 40.
  • Lorsque le magma se solidifie, le potassium 40 se désintègre peu à peu en argon.
  • Si on arrive à déterminer la proportion potassium 40 / argon dans la roche, on peut ainsi la dater. Par exemple si ce rapport vaut 1, c’est que la moitié du $*\ce{^40K}*$ initialement présent s’est désintégré en $*\ce{^40Ar}*$ et donc que la roche a 1,25 Ga.

1. Écrire l’équation de la désintégration du potassium 40.

2. Établir la loi de décroissance radioactive permettant de connaître la quantité $*N*$ de noyaux d’un isotope radioactif en fonction de la quantité initiale $*N_0*$ et du temps qui s’est écoulé depuis l’instant initial.

3. Un paléontologue cherche à dater une roche volcanique. Il fait mesurer par un laboratoire le rapport isotopique $*\ce{^40K}*$ / $*\ce{^40Ar}*$ et le résultat obtenu est 3,4 ± 0,1. Donner un encadrement de l’âge de cette roche.

Correction

1. $*\ce{_19^40K → _18^40Ar + _1^0e^+}*$

2. Durant un temps infinitésimal $*\mathrm{d}t*$, la quantité de noyaux qui se désintègre est proportionnelle à cette durée et au nombre $*N*$ total de noyaux. Donc la variation $*\mathrm{d}N*$ de noyaux est égale à : $µ \mathrm{d}N = -\lambda N \mathrm{d} t µ$ On obtient l’équation différentielle : $µ \frac {\mathrm{d}N}{\mathrm{d}t} = - \lambda N µ$ On sait que la solution de cette équation différentielle est : $µ N(t)=N_0 e^{-\lambda t} µ$ Avec $*N_0*$ la quantité de noyaux à $*t*$ = 0

3. La quantité de noyaux de $*\ce{^40K}*$ présents à l’instant $*t*$ est $*N(t)=N_0 e^{-\lambda t}*$
La quantité de noyaux de $*\ce{^40Ar}*$ formés à l’instant $*t*$ est $*N_\mathrm{Ar} (t) = N_0 - N(t) = N_0 (1-e^{-λt})*$
Donc le rapport $*\ce{^40K}*$ / $*\ce{^40Ar}*$ (noté $*R*$) s’écrit : $µ R = \frac {N_0 e^{-λt}}{N_0 (1-e^{-λt})} = \frac{e^{-λt}}{1-e^{-λt}} µ$ D’autre part, $* λ = \dfrac {\ln(2)}{t_{1/2}}*$
Donc $*λ*$ = 5,55·10-10 année-1
Il ne reste qu’à isoler $*t*$, $*R*$ et $*λ*$ étant connus : $µ \begin{aligned} R(1-e^{-λt}) &= e^{-λt} \\ R &= e^{-λt} (1+R) \\ -λt &= \ln⁡(\frac R{1+R}) \\ t &= \frac 1λ·\ln⁡(\frac {1+R}R) \end{aligned} µ$ On trouve que $*t*$ est compris entre 453 et 477 Ma.