P10. Mécanique des fluides

La mécanique des fluides est un domaine de la physique consacré à l’étude du comportement des fluides (liquides, gaz et plasmas) et des forces internes associées. Elle se divise en deux parties : la statique des fluides qui est l’étude des fluides au repos et la dynamique des fluides, qui est l’étude des fluides en mouvement.

La statique des fluides a été abordée en première dans ce chapitre. Merci d’aller vous rafraîchir la mémoire 😊

Poussée d’Archimède

Expliquer qualitativement l’origine de la poussée d’Archimède.
Utiliser l’expression vectorielle de la poussée d’Archimède.

La poussée d’Archimède, c’est la force qu’un fluide exerce sur un corps plongé dedans (partiellement ou complètement). Cette force est verticale, orientée vers le haut.

Origine de la poussée d’Archimède

Il est assez facile de comprendre intuitivement d’où vient cette force.

Faisons une expérience de pensée et plongeons un objet ayant la forme d’un pavé de manière à l’immerger complétement dans de l’eau.
Les forces pressantes exercées par le fluide sur les faces verticales n’ont aucune composante verticale. Elles ne contribuent à pousser l’objet ni vers le haut ni vers le bas.

Les forces qui s’exercent sur les faces horizontales, par contre, poussent l’objet vers le haut (pour les forces qui s’exercent sur le fond de l’objet) ou vers le bas (pour celle qui s’exercent sur la face supérieure de l’objet).

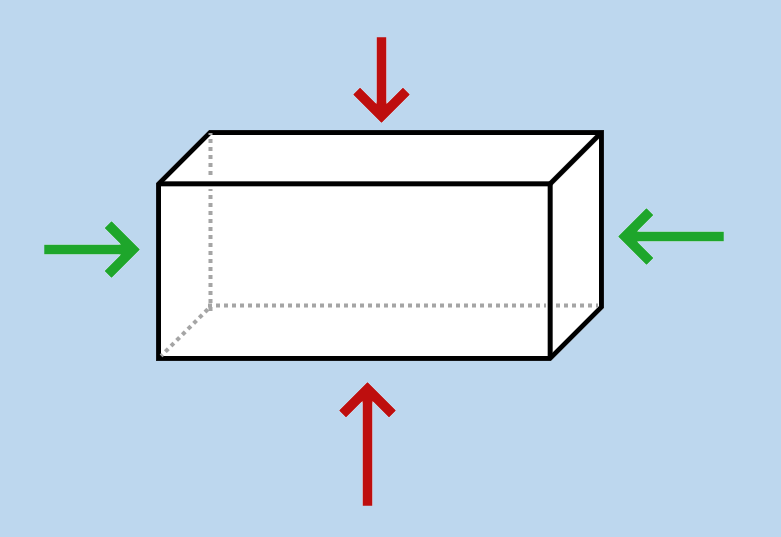
Force s’exerçant sur un pavé plongé dans un fluide. Les forces s’exerçant sur la face avant et la face arrière ne sont pas représentées par souci de clarté.

Or, et nous l’avons vu en première – c’est pour ça que je vous ai demandé de vous rafraîchir la mémoire – la pression dans un fluide augmente à mesure que l’on descend (c’est-à-dire qu’on se dirige dans le sens du champ de pesanteur).

Donc la pression dans l’eau au niveau du fond de l’objet est plus forte que la pression au niveau du haut de l’objet. Du coup, les forces pressantes qui poussent l’objet vers le haut sont plus intenses que celles qui poussent l’objet vers le bas. Cette différence de force, c’est… la poussée d’Archimède.

TP Poussée d’Archimède

Mettre en œuvre un dispositif permettant de tester ou d’exploiter l’expression de la poussée d’Archimède.

Mesurer la poussée d’Archimède

Proposer et réaliser une expérience permettant de montrer que la poussée d’Archimède est égale au poids du volume d’eau déplacé.

Vérifier que vos mesures sont cohérentes si vous changez la densité du liquide étudié (par exemple de l’éthanol).

Ballast de sous-marin

Réaliser un ludion. En quoi ce petit montage amusant illustre-t-il le principe des ballasts de sous-marins ?

Expression de la poussée d’Archimède

La poussée d’Archimède, souvent notée $*\vec{\mathit{\Pi}}*$, est une force verticale orientée vers le haut, dont la valeur est égale au poids du volume de fluide déplacée par l’objet.

$* \vec{\mathit{\Pi}} = -\rho V \vec{g} *$

$*\rho*$ : masse volumique du fluide
$*V*$ : volume de fluide déplacé
$*\vec{g}*$ : champ de pesanteur

Ligne de flottaison

On modélise la coque d’un bateau par un prisme de longueur 10 m et de hauteur 2 m. L’angle formé par les deux pans de coque est de 60 °.

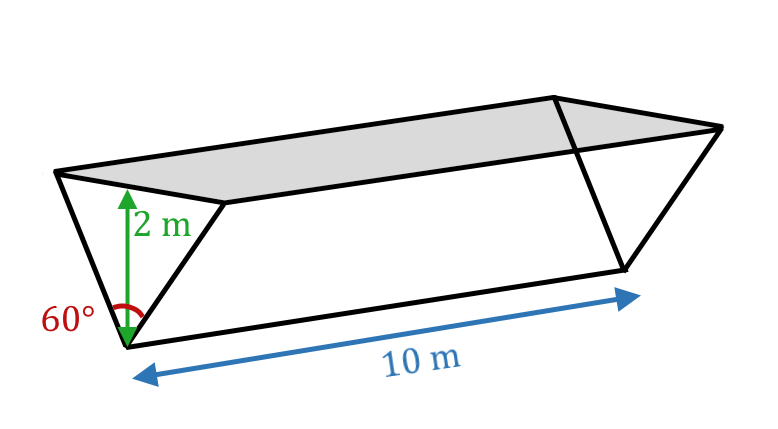
1. Démontrer que la hauteur $*h*$ de coque submergée est donnée par la relation : $µ h = \sqrt{\dfrac{m}{\rho_{eau}·\ell·\tan{30°}}} µ$ avec $*\ell*$ la longueur du bateau (10 m) et $*m*$ sa masse.

2. La masse du bateau à vide est de 5,8 t. Calculer la hauteur de coque submergée.

3. Pour des raisons de sécurité, on souhaite que le bateau ne s’enfonce jamais plus de 1,50 m dans l’eau. Quelle charge peut-il embarquer ?

Correction

1. Le surface immergée des triangles avant et arrière vaut $*S = h^2·\tan{30°}*$.
Donc le volume immergé vaut $*V = S·\ell = \ell·h^2·\tan{30°}*$
Comme le bateau flotte, la poussée d’Archimède compense le poids, donc : $µ \rho_{eau}·\ell·h^2·\tan{30°}·g = mg µ$ Yapuka isoler $*h*$… 😊

2. Pour $*m*$ = 5,8·10³ kg, on trouve $*h*$ ≃ 1,2 m. Le bateau s’enfonce de 1,2 m dans lorsqu’il est vide.

3. La masse totale ne doit pas excèder 9,7 t, soit environ 4 t de chargement.

Écoulement d’un fluide

Exploiter la conservation du débit volumique pour déterminer la vitesse d’un fluide incompressible.

Modèle de la particule fluide

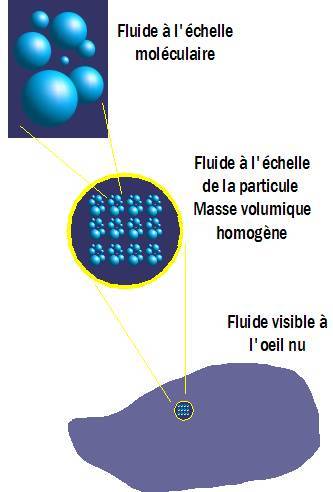
Un fluide est modélisé par un grand nombre de petits volumes appelés « particules fluides ».

Si on s’intéresse à de l’eau, ces particules fluides peuvent être imaginées comme de minuscules volumes d’eau qui, pris ensemble, constituent l’ensemble du volume d’eau qu’on étudie.

Les particules fluides doivent être petites devant les échelles de l’écoulement : elles n’auront bien sûr par la même taille si on s’intéresse à de grands courants océaniques ou à l’écoulement de l’eau dans une rivière ou un tuyau d’arrosage.

Cependant, la taille d’une particule fluide est toujours très grande devant la taille des molécules qui la composent. On considère donc les fluides comme des milieux continus, C'est-à-dire que l'on admet que des propriétés telles que la densité, la pression, la température, et la vitesse sont prises pour étant bien définies à des points « infiniment petits », et changent progressivement d'un point à l'autre. La nature discrète et moléculaire d'un fluide est donc ignorée.

La définition de Wikipédia

Le terme particule fluide est utilisé en mécanique des fluides pour désigner un volume élémentaire de fluide d'échelle mésoscopique. L’échelle mésoscopique est typiquement de l'ordre du micromètre. C'est une échelle d'une part suffisamment petite pour que la grandeur étudiée puisse être considéré comme ponctuelle, et d'autre part suffisamment grande pour pouvoir considérer le milieu comme continu, c'est-à-dire ne pas avoir à faire une étude discrète de toutes les molécules.

Mouvement du fluide

L’étude du mouvement d’un fluide se fait de la même manière que celle d’un solide : on se place dans un référentiel galiléen et on commence par définir un système d’étude, ici une particule de fluide.

Le mouvement du fluide est décrit par un champ de vitesse, qui est l’ensemble des vecteurs vitesse de toutes les particules du fluide.

Écoulement incompressible : on considère que la particule de fluide ne peut pas changer de volume au cours du déplacement. C’est le cas des fluides incompressibles, c’est-à-dire les liquides.

Écoulement permanent (ou stationnaire) : c’est un écoulement stable dans le temps. Cela se traduit par un champ de vitesse qui ne varie pas dans le temps.

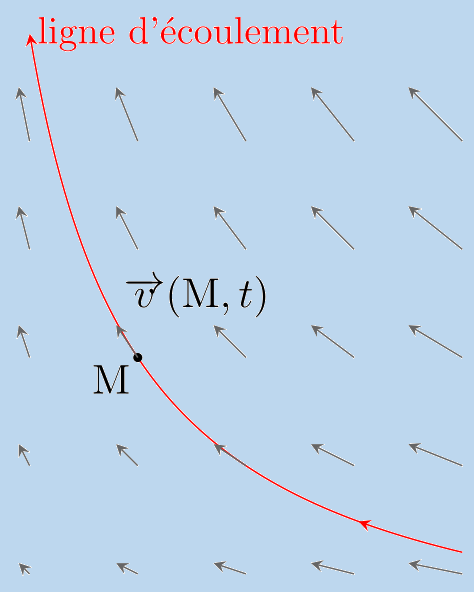
Ligne de courant

Une ligne de courant est une courbe de l’espace décrivant le mouvement d’un fluide et qui, à tout instant, possède en tout point une tangente parallèle à la vitesse des particules du fluide.

Lorsque l'écoulement est permanent, le mouvement d’une poussière (de masse volumique égale à celle du fluide) emportée par cet écoulement trace une ligne de courant.

Conservation du débit volumique

Pour caractériser les écoulements, on utilise une grandeur appelée le débit volumique $*D_V*$ :

$* D_V = \dfrac{\mathrm{d}V}{\mathrm{d}t} *$

$*D_V*$ : débit volumique (m³·s^-1)
$*V*$ : volume de fluide écoulée (m³)
$*t*$ : temps (s)

La masse d’une particule fluide reste constante au cours du temps. Pour un écoulement incompressible, le volume d’une particule fluide reste constant même si elle se déforme. Il existe alors une relation entre le débit volumique $*D_V*$ et la surface $*S*$ traversée :

$* D_V = S·v *$

$*D_V*$ : débit volumique (m³·s^-1)
$*v*$ : vitesse d’écoulement (m·s^-1)
$*S*$ : surface traversée par l’écoulement (m²)

Débit d’un robinet

Exprimer, puis calculer la vitesse de l’écoulement de débit volumique 5,1 L·min^-1 sortant d’un robinet de section 1,3 cm².

Si le fluide est incompressible, il y a conservation du débit volumique. Le long d’un tube de courant, le débit volumique est constant et uniforme : $µ D_V = v_1⋅S_1 = v_2⋅S_2 µ$

Cette loi de conservation est très utile pour calculer des vitesses en différents points d’un écoulement.

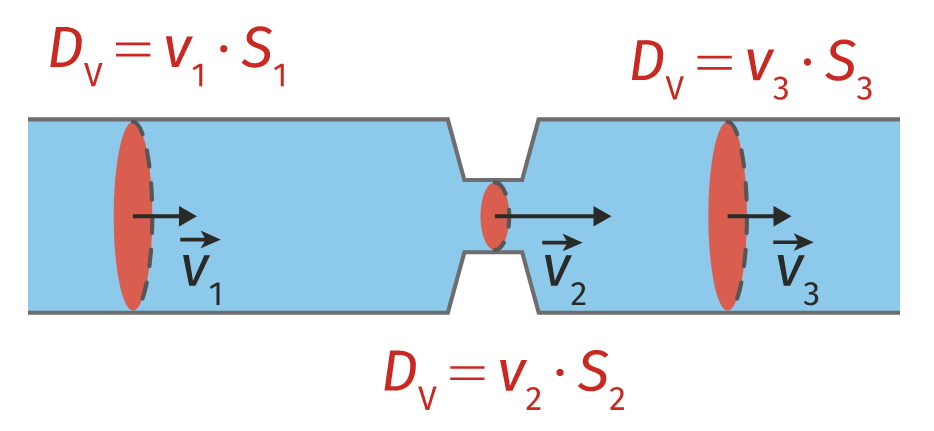
Écoulement dans un tuyau de section variable

Conservation du débit

On adapte maintenant un embout au robinet de manière à réduire la section de sortie. Cet embout a une sortie circulaire de 3 mm de diamètre. Quelle est la nouvelle vitesse d’écoulement ?

Relation de Bernouilli

Exploiter la relation de Bernoulli pour étudier qualitativement et quantitativement l’écoulement d’un fluide incompressible en régime permanent.

Relation de Bernoulli

Pour un écoulement incompressible et permanent d’un ﬂuide parfait, dans un champ de pesanteur uniforme, la conservation de l’énergie implique que la quantité $µ p + \frac 12 \rho v^2 + \rho g z µ$ est constante le long d’une ligne de courant.

Ces trois termes représentent des énergies volumiques :

$*p*$ est l’énergie potentielle volumique associées aux forces pressantes.
$*\frac 12 \rho v^2*$ est l’énergie cinétique volumique.
$*\rho g z*$ est l’énergie potentielle de pesanteur volumique.

Pour vous convaincre « physiquement » que la pression est une énergie potentielle volumique, vous pouvez raisonner de la manière suivante :

Considérons un tube cylindrique de gaz parfait de longueur $*\ell*$ et de section $*S*$. Une des extrémité de ce tube est fermée et l’autre est compressible par un piston.

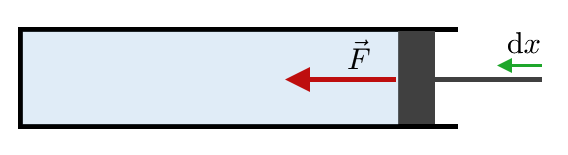
Lorsqu’on pousse le piston sur une toute petite distance $*\mathrm{d}x*$ suffisament lentement pour que la température du gaz ne change pas (compression isotherme), le travail de la force, fournit au gaz est : $µ F\mathrm{d}x = PS\mathrm{d}x = - P\mathrm{d}V µ$ Cette relation montre bien que l’énergie communiquée au gaz sous forme d’énergie potentielle de pression correspond à une pression multpliée par un volume.

La pression est donc bien une énergie volumique (autrement dit 1 Pa = 1 J·m^-3)

TP Loi de Bernoulli

Mettre en œuvre un dispositif expérimental pour étudier l’écoulement permanent d’un fluide et pour tester la relation de Bernoulli.

Objectif : vérifier si, dans la situation suivante, l’énergie mécanique du fluide reste à peu près constante (c’est-à-dire si la relation de Bernoulli est vérifiée ou non).

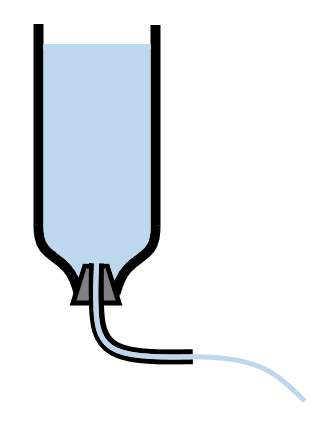
Questions préalables

1. Quelle est la pression à la surface de l’eau en haut de la bouteille ?

2. Quelle est la pression de l’eau juste à la sortie du tuyau ?

3. Comment peut-on faire pour estimer la vitesse de sortie de l’eau ?

Mesures

Réaliser les mesures nécessaires pour déterminer la vitesse de l’eau à différents moments de la vidange.

Exploitation

Vérifiez que la relation de Bernoulli est vérifiée au cours de l’écoulement.

Éléments de réponses

Réponse aux questions préalables

À la surface de l’eau comme à la sortie du tuyau, l’eau est à l’air libre, donc sa pression est celle de l’atmosphère.
Plusieurs possibilités pour mesurer la vitesse de l’eau à la sortie du tuyau :

mesurer le débit du tuyau pendant quelques secondes, en faisant l’approximation que ce débit est constant au cours de la mesure ;
Modéliser la parabole formée par le jet d’eau pour en extraire la valeur de la vitesse de l’eau (voir chapitre P2 – je sais, c’était il y a longtemps… 👴)

Résultats des mesures

Par mesure du débit : les débits mesurés sont de l’ordre de 80 mL en 5 secondes, soit environ 16 ml·s^-1 (16·10^-6 m³·s^-1 en unité S.I).
le diamètre intérieur du tuyau est de 4 mm, soit une section de 1,3·10^-5 m².
On peut en déduire la vitesse de sortie de l’eau : $*v_B*$ = 16·10^-6 ÷ 1,3·10^-5 ≃ 1,2 m·s^-1.

Par modélisation de la trajectoire du jet d’eau :

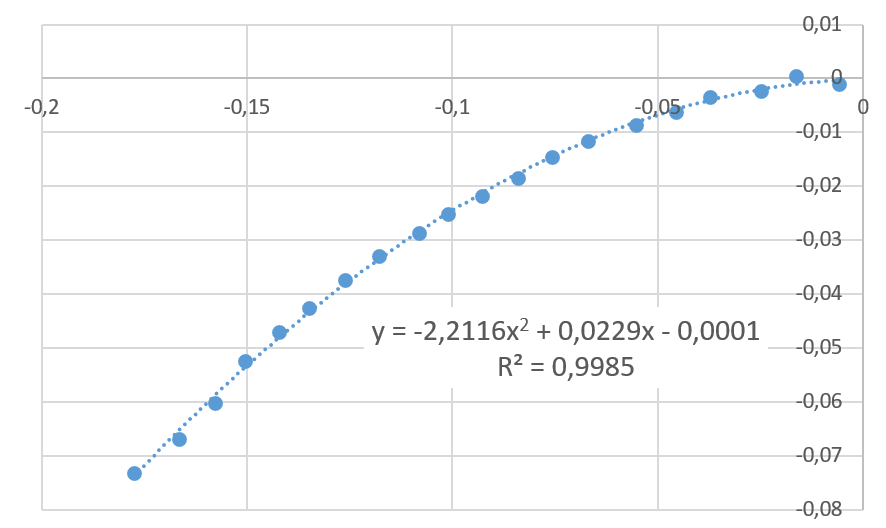
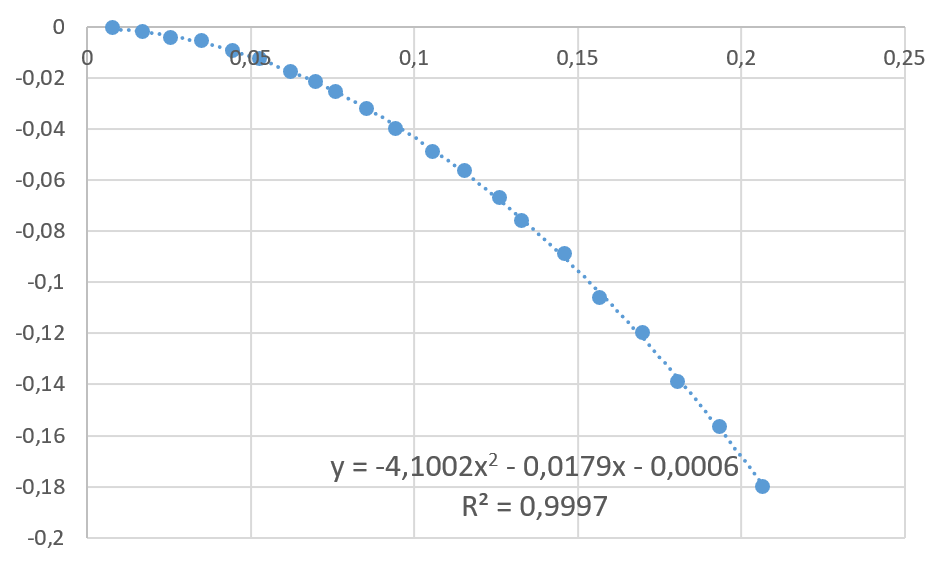
Le facteur devant $*x^2*$ (-2,2) vaut $* - \frac 12 \frac g{v_0} *$ (voir chapitre P2) car le vecteur vitesse initiale est horizontal.
On en déduit que $*v_0*$ ≃ 1,5 m·s^-1. Les deux valeurs sont relativement proches.

Vérification de la loi de Bernoulli. On doit vérifier qu’entre un point A pris à la surface de l’eau dans la bouteille et un point B pris à la sortie du tuyau, on a $µ p_A + \frac 12 \rho v_A^2 + \rho g z_A = p_B + \frac 12 \rho v_B^2 + \rho g z_B µ$ Les deux pressions $*p_A*$ et $*p_B*$ sont égales. Si on prend $*z_B*$ comme origine des altitudes et en simplifiant par la masse volumique de l’eau, ça revient à vérifier l’égalité $µ \frac 12 v_A^2 + g z_A = \frac 12 v_B^2 µ$ $*v_A*$ est de l’ordre de 3 mm par seconde, $*z_a*$ vaut environ 23 cm. On obtient donc : $µ \frac 12 v_A^2 + g z_A = \frac 12 0,003^2 + 9,8×0,23 = 2,25 µ$ $µ \frac 12 v_B^2 = \frac 12 1,5^2 = 1,13 µ$ Les résultats s’expriment en m²·s^-2.

On voit que la relation de Bernoulli n’est pas vérifié. L’énergie volumique à la surface de l’eau est environ deux fois plus grande que l’énergie volumique à la sortie du tube.

Conclusion : lors de cet écoulement, les frottements ne sont pas du tout négligeables. En fait, le diamètre du tuyau est petit et ce dernier est assez long, créant ainsi des frottements assez importants.

Pour valider cette hypothèse, on peut refaire l’expérience avec une bouteille dans laquelle on a fait un trou (assez gros – environ 6 à 7 mm de diamètre). L’eau sort directement par le trou, limitant ainsi les frottements.

Par les mêmes calculs, on trouve que la vitesse d’écoulement vaut 1,1 m·s^-1. La hauteur d’eau au-dessus du jet est de 7,8 cm, la vitesse $*v_A*$ est d’environ 2 à 3 mm par seconde.

Ce qui nous donne : $µ \frac 12 v_A^2 + g z_A = \frac 12 0,003^2 + 9,8×0,078 = 0,76 µ$ $µ \frac 12 v_B^2 = \frac 12 1,1^2 = 0,61 µ$ Il subsiste alors une différence, mais bien moins grande (0,76 m²·s^-2 à la surface contre 0,61 m²·s^-2)

Ceci montre que les frottements sont moins importants dans cette situation.

Vidange d’un bac

On considère un bac de la forme d’un parallélépipède rectangle de surface horizontale 20 × 30 cm². Au fond de ce bac se trouve un tuyau de 0,5 cm de diamètre.

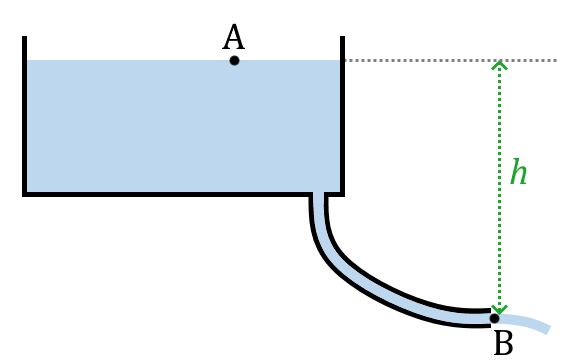
1. Appliquer littéralement la relation de Bernoulli aux points A et B.

2.a. Le fluide est de l’eau. On se place sur Terre. La hauteur $*h*$ vaut 30 cm. Quelle est la vitesse d’écoulement en B ?

2.b. En déduire le débit d’eau sortant du tuyau.

3. Le débit est-il constant au cours de la vidange ?

Effet Venturi

Ce qu’en dit Wikipédia

L’effet Venturi, du nom du physicien italien Giovanni Battista Venturi, est le nom donné à un phénomène de la dynamique des fluides, selon lequel un fluide en écoulement subit une dépression là où la vitesse d'écoulement augmente, ou encore là où la section d'écoulement se rétrécit.

L’effet est une manifestation du principe de conservation de l’énergie (formalisé dans le cas des écoulements fluides par le théorème de Bernoulli) et peut s’énoncer de la façon suivante : dans le cas d’un écoulement fluide horizontal, lorsque la vitesse d’écoulement augmente, la pression diminue nécessairement.

La pression au point 1 est plus grande qu'au point 2. Et la vitesse du fluide au point 2 est plus grande qu’au point 1.

Une vidéo très intéressante sur une application de l’effet Venturi (e-penser)
Comment une pompe à essence s'arrête

Analysons un peu ce que vous venez de lire… D’après la relation de Bernoulli (aussi appelé théorème de Bernoulli), nous dit que $µ p_1 + \frac 12 \rho v_1^2 + \rho g z_1 = p_2 + \frac 12 \rho v_2^2 + \rho g z_2 µ$ Les indices 1 et 2 font référence aux points 1 et 2 du schéma ci-dessous.

L’altitude ne change pas entre ces deux points. Par contre $*v_2*$ > $*v_1*$, donc nécessairement $*p_1*$ > $*p_2*$

On peut même aller au-delà d’une comparaison qualitative. Allez hop ! Un petit exercice pour vérifier ça !

Trompe à eau

Une trompe à eau est un dispositif permettant d’aspirer de l’air en utilisant le débit d’eau d’un robinet.

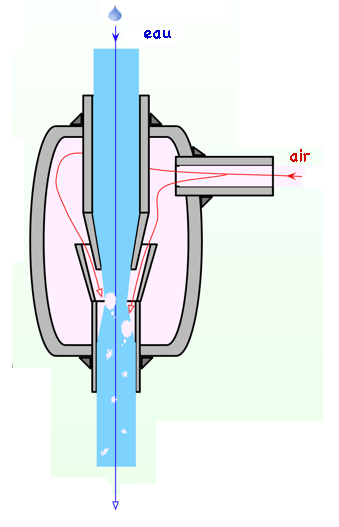
Supposons que la section du conduit d’entrée d’eau soit de 12 mm² et que celui-ci se rétrécisse jusqu’à 3 mm² au niveau de sa sortie dans la zone d’aspiration de l’air.

Le robinet est ouvert de manière à avoir un débit de 30 mL·s^-1. La pression à la sortie du robinet vaut 1,1 bar. On négligea la variation d’énergie potentielle du liquide lors de sa descente dans la trompe.

Question

Quelle sera la valeur de la pression dans la zone d’aspiration ?

Physique & Chimie au lycée

Cours de physique-chimie pour les classes de 1^ère et Terminale