C3. Titrages
Un titrage, c’est un type de dosage particulier. Rappelez-vous, lorsqu’on fait un dosage, on cherche à déterminer une concentration. Un titrage, c’est un dosage qui implique une réaction chimique. En fait, l’idée est d’introduire en quantité connue un réactif titrant pour qu’il réagisse entièrement avec le réactif titré, sans ajouter le réactif titrant (qu’on abrège parfois par le terme « titrant »). Ça nécessite pas mal de conditions qu’on va étudier dans ce chapitre.
Titre massique & densité
- Réaliser une solution de concentration donnée en soluté apporté à partir d’une solution de titre massique et de densité fournis.
Bon, ce paragraphe est assez peu lié aux titrages en général.
On va commencer par clarifier le terme de « titre ». Le titre d’une solution, c’est sa concentration. Ces deux termes sont synonymes. Vous êtes donc maintenant capables de comprendre la phrase suivante : « Dans un titrage, on titre le titré avec un titrant pour connaître son titre ». 😄
Mais trêve de plaisanterie. Il arrive, sur certains flacons (notamment ceux d’acides concentrés), que l’on lise les informations suivantes :

Il y a également sur l’étiquette la densité de la solution (pour l’acide chlorhydrique concentré $*d*$ = 1,19). Vous devez savoir, à partir de ces informations, calculer la concentration molaire de cette solution. Comment faire ?
Le « 37 % » correspond au titre massique de la solution. Ça veut dire que 100 g de solution contiennent 37 g d’acide chlorhydrique pur.
De là, en utilisant la densité, vous pouvez calculer que :
• 100 g de solution = 84,0 mL ;
• 37 g d’acide chlorhydrique = 37/36,5 = 1,01 mol.
La masse molaire de ce qui est appelé improprement acide chlorhydrique, mais qui est en fait du chlorure d’hydrogène $*\ce{HCl}*$, vaut 36,5 g·mol-1, c’est généralement aussi écrit sur le flacon.
Ce qui fait une concentration de $*c = \frac nV =*$ 12,0 mol·L-1.
Je me suis toujours demandé pourquoi les fabricants n’indiquaient pas cette concentration sur l’étiquette, ce qui éviterait des calculs quand on a un trou de mémoire. 😔
Allez, un petit exercice pour vérifier si vous avez bien compris, et on rentre dans le cœur du chapitre
Acide nitrique concentré
On peut lire, sur un flacon d’acide nitrique $*\ce{HNO3}*$ concentré, les indications suivantes :
- Titre massique : 69 %
- Densité : 1,41
- Masse molaire : 63 g·mol-1
1. Calculer la concentration molaire de cet acide
2. Dans cette solution, qui est majoritaire en qdm : l’eau ou l’acide nitrique ?
Correction
1. 1 L pèse 1,41 kg. Donc 1 L de cette solution contient 1,41×0,69 = 0,973 kg d’acide nitrique pur. Soit une qdm de 973÷63 ≃ 15,4 mol·L-1.
2. 1 L de cette solution contient 1,41 – 0,973 = 0,437 kg, soit 24,3 mol d’eau. L’eau est tout de même majoritaire.
Généralités sur les titrages
Tout ce paragraphe n’est qu’un rappel de ce qui a été vu au chapitre C5 de 1e.
Réaction de titrage
Un titrage direct s’appuie sur une réaction de titrage.
- On introduit un réactif titrant
- de manière à connaître à chaque instant quelle est la quantité introduite,
- dans un volume parfaitement connu de solution contenant le titré.
Le titrant réagit avec le titré.
Lorsqu’on a introduit le titrant
- de manière à avoir réagi avec tout le titré,
- mais sans l’avoir ajouté en excès,
alors on peut en déduire quelle était la qdm initiale de titré dans le volume de solution dont on disposait.
Le moment clé où on a ajouté le titrant en quantité stœchiométrique avec le titré est appelé l’équivalence
Si vous prenez le temps de réfléchir à toutes les conditions à respecter, vous réaliserez que ça fait pas mal de contraintes sur la réaction de titrage.
Contraintes sur la réaction de titrages
La réaction de titrage doit être :
- rapide (sinon, on ne sait pas quand arrêter l’ajout d’espèce titrante).
- totale (sinon, on ne dosera pas toute l’espèce à titrer).
- spécifique de l’espèce à titrer (si elle réagit aussi avec une autre espèce, on ne peut pas déterminer la quantité de matière de l’espèce à titrer).
De plus :
- l’équivalence doit être repérable (sinon, on ne sait pas quand arrêter l’ajout d’espèce titrante).
Montage expérimental
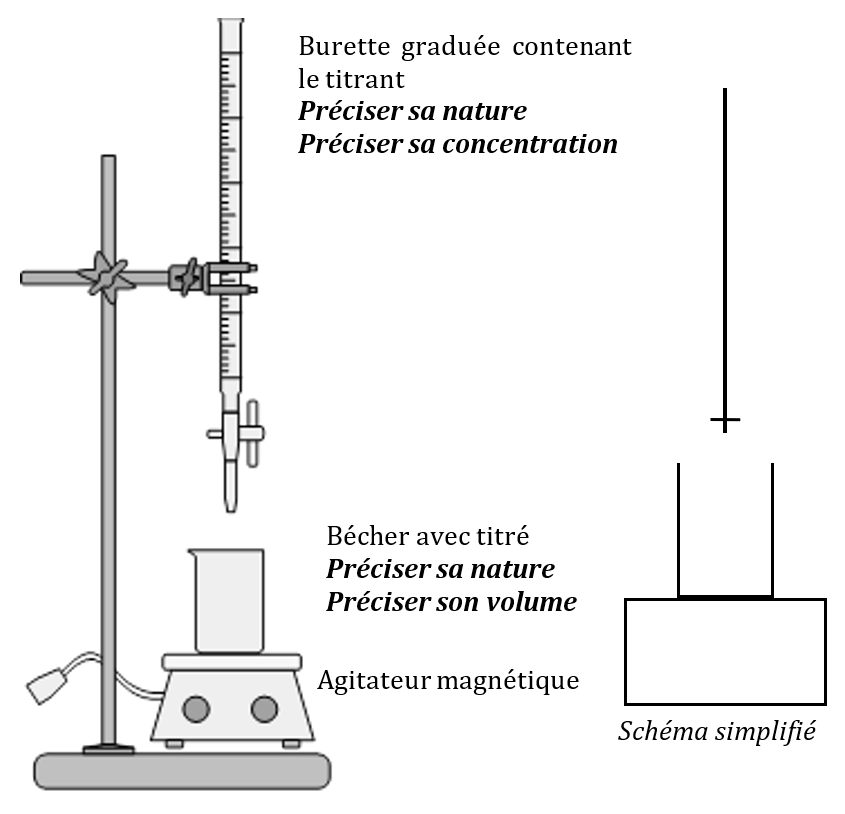
La burette sert à connaître le volume de titrant versé à tout moment.
La solution contenant le titré doit avoir été prélevée avec une pipette jaugée pour qu’on connaisse son volume le plus précisément possible.
Lorsque vous devrez faire un schéma du montage, faites toujours le schéma simplifié.
L’équivalence
Je vous l’ai déjà dit plus haut, mais c’est un point capital à retenir :
Relation entre les qdm de titrant et de titré à l’équivalence
Imaginons une réaction chimique générale dont le bilan est : $µ a\mathrm{A} + b\mathrm{B} \rightarrow c\mathrm{C} + d\mathrm{D} µ$
Disons, pour fixer les idées, que $*\mathrm{A}*$ est le titrant et $*\mathrm{B}*$ le titré. Quelle relation on a à l’équivalence ? Eh bien, rappelez-vous des tableaux d’avancement en 1e : $µ \frac {n_{Ae}}a = \frac {n_{Bi}}b µ$ où $*n_{Ae}*$ est la qdm de titrant introduite à l’équivalence et $*n_{Bi}*$ est la qdm de titré présente dans le bécher avec le début du titrage.
Remarque : pour certaines réactions, $*a=b*$ et donc la proportion stœchiométrique est atteinte lorsque les deux réactifs ont été introduits en même quantité. Mais ce n’est pas nécessairement le cas pour tous les titrages. Pas de généralisation hâtive, donc, sous peine de vous planter le jour où je vous tendrai ce piège. 😈
Choix du volume de titré à prélever
Voilà un problème qui peut parfois être un peu délicat. Si vous prélevez trop de titré, vous n’arriverez pas à l’équivalence même après avoir vidé la burette. Et vous pouvez donc tout recommencer. Et si vous n’en prélevez pas assez, votre volume équivalent $*V_e*$, qui est le volume de titrant versé pour atteindre l’équivalence, va être très petit et votre dosage sera très imprécis – il faut tout recommencer aussi. Il faut donc trouver le « juste milieu ». 😊
L’idéal, en termes de précision, est d’avoir un volume $*V_e*$ qui soit compris entre la moitié et les trois quarts du volume de la burette.
Bonne question ! Rappelez-vous ce que je vous avais dit à propos du dosage conductimétrique par étalonnage. Il faut qu’on ait une idée approximative de la concentration du titré. Si vraiment vous n’avez aucune idée de sa concentration, il va falloir faire deux dosages : un plus imprécis, mais qui va vous permettre d’avoir une idée de la concentration du titré, puis un deuxième pour lequel vous adapterez le volume de solution titrée à doser pour optimiser la précision de votre titrage.
Un petit exemple pour fixer les idées.
On veut doser de l’acide chlorhydrique $*\ce{(H3O+ ; Cl^-)}*$ dont la concentration attendue est d’environ 40 à 80 mmol·L-1, par de la soude $*\ce{(Na+ ; HO^–)}*$ de concentration 10,0 mmol·L-1.
L’équation de la réaction est : $*\ce{H3O+ + HO^– \rightarrow 2 H2O}*$. Quel volume d’acide doser ?
L’acide est environ 4 à 8 fois plus concentré que la soude. Donc, en tenant compte de la stœchiométrie de la réaction (1 mol de $*\ce{H3O+}*$ réagit avec 1 mol de $*\ce{HO^-)}*$ le volume de soude versé à l’équivalence sera 4 à 8 fois plus grand que le volume d’acide dosé. Si l’on souhaite que $*V_E*$ soit entre environ 20 mL et environ 40 mL, il faut doser un volume d’acide $*V_A*$ de 5,0 mL.
✋ Il est parfois nécessaire de préalablement diluer le réactif titrant ou le réactif titré si les écarts de concentration sont très importants.
TP Représenter des qdm au cours d’un dosage
- Capacité numérique : représenter, à l’aide d’un langage de programmation, l’évolution des quantités de matière des espèces en fonction du volume de solution titrante versé.
- Établir la composition du système après ajout d’un volume de solution titrante, la transformation étant considérée comme totale.
Objectif : représenter, sur un graphique en barres animé, l’évolution des quantités de matière en fonction du temps.
Prenons un réaction déjà vue en classe de première :
$µ \ce{ I2 + 2 S2O3^{2-} \rightarrow 2I^- + S4O6^{2-}} µ$
Imaginons que, dans un bécher, on dispose de 5 mmol de $*\ce{I2(aq)}*$. On ajoute, mmol par mmol, une solution de thiosulfate de sodium ($*\ce{2Na+ ; S2O3^{2-}}*$), jusqu’à en avoir ajouté 20 mmol.
Créer un graphique en barres animé montrant les qdm de : $*\ce{I2}*$ ; $*\ce{S2O3^{2-}}*$ ; $*\ce{S4O6^{2-}}*$ ; $*\ce{I^-}*$ et $*\ce{Na+}*$ ; pour chaque ajout de 1 mmol.
Ce graphique devra avoir pour titre « Avant l’équivalence » ou « Après l’équivalence » selon qui est le réactif en excès. (Oui, c’est une petite déco inutile mais classe… 😊)
Je vous ai préparé les outils nécessaires dans la section Python… Merci qui ?
Éléments de correction
Comment évoluent les qdm lors de l’ajout mmol par mmol de thiosulfate ? On va noter $*i*$ la qdm de thiosulfate ajoutée.
Un petit tableau indiquant les qdm des différentes espèces dans le bécher après ajout de $*i*$ mmol de $*\ce{S2O3^{2-}}*$ (toutes les valeurs sont en mmol) :
| $*i*$ | $*\ce{I2}*$ | $*\ce{S2O3^{2-}}*$ | $*\ce{I^-}*$ | $*\ce{S4O6^{2-}}*$ | $*\ce{Na+}*$ |
|---|---|---|---|---|---|
| 0 | 5 | 0 | 0 | 0 | 0 |
| 1 | 4,5 | 0 | 1 | 0,5 | 2 |
| $*i*$ ≤ 10 | 5-0.5$*i*$ | 0 | $*i*$ | 0,5$*i*$ | 2$*i*$ |
| $*i*$ > 10 | 0 | $*i*$-10 | 10 | 5 | 2$*i*$ |
Attention, ce tableau n’est pas un tableau d’avancement. Mais il se construit grâce à un tableau d’avancement.
Voici un code possible.
import matplotlib.pyplot as plt
x=range(5)
for i in range(21):
plt.cla()
axes = plt.gca()
axes.set_ylim(0, 41)
if i <= 10 :
n_I2 = 5-0.5*i
n_thio = 0
n_I = i
n_tetra = 0.5*i
n_Na = 2*i
plt.title("Avant l’équivalence")
else :
n_I2 = 0
n_thio = i-10
n_I = 10
n_tetra = 5
n_Na = 2*i
plt.title("Après l’équivalence")
plt.bar(
x,
[n_I2, n_thio, n_I , n_tetra, n_Na],
width = 0.5,
color = ['indianred', 'lightblue', 'lightskyblue', 'peachpuff', 'grey']
)
plt.xticks(x, ('$\mathrm{I}_2$',
'$\mathrm{S}_2\mathrm{O}_3^{2-}$',
'$\mathrm{S}_4\mathrm{O}_6^{2-}$',
'$\mathrm{I}^-$',
'$\mathrm{Na}^+$') )
plt.ylabel('qdm (mmol)')
plt.pause(0.2)
plt.show()
Choix d’un volume de solution à titrer
On souhaite titrer une solution d’acide chlorhydrique $*\ce{(H3O+ ; Cl^-)}*$ de concentration attendue entre 0,08 et 0,18 mol·L-1.
On dispose de soude $*\ce{(Na+ ; HO^–)}*$ à 0,10 mol·L-1, d’une burette graduée de 25 mL et de pipettes jaugées (5 mL, 10 mL, 15 mL et 20 mL).
Quel volume d’acide doit-on doser si on veut un volume versé à l’équivalence le plus proche possible de 20 mL, sans excéder 20 mL ?
Correction
On calcule le volume d’acide $*V_A*$ à prélever pour avoir un volume à l’équivalence $*V_{BE}*$ égal à 20 mL au maximum, c’est-à-dire pour la concentration $*C_A*$ maximale attendue (0,18 mol·L-1). On a ici $µ V_A = \frac {C_BV_{BE}}{C_A} µ$ soit un volume $*V_A*$ = 11,1 mL. On est donc obligé (à cause des pipettes jaugées) de prélever 10 mL d’acide (si on en prend 15 mL, le volume de base versé à l’équivalence pourrait être trop important).Titrage pH-métrique
- Exploiter un titrage pour déterminer une quantité de matière, une concentration ou une masse.
Un titrage pH-métrique, ou plus exactement un titrage avec suivi pH-métrique, est un titrage pour lequel l’équivalence est repérée grâce à la variation du pH. Il s’agit d’un titrage acide-base : on titre une solution acide par une solution basique ou l’inverse.
Réaction de titrage acido-basique
Que l’on titre un acide par une base ou l’inverse, la réaction de titrage est toujours une réaction acido-basique (d’où le nom du titrage).
Titrage d’un acide par une base forte
$µ\ce{AH + HO- \rightarrow A- + H2O}µ$
Titrage d’une base par un acide fort
$µ\ce{B + H3O+ \rightarrow BH+ + H2O}µ$
Remarque : la signification du terme « fort » dans le contexte d’un acide ou d’une base sera vu plus en détails dans le chapitre C6. Contentez-vous pour l’instant de retenir que dans une solution d’acide fort à $*x*$ mol·L-1, $*\ce{[H3O+]} = x*$ mol·L-1.
Même principe pour une base forte : dans une solution de base forte à $*x*$ mol·L-1, $*\ce{[HO-]} = x*$ mol·L-1.
Suivi pH-métrique
On suit l’évolution du pH en fonction du volume de réactif titrant versé tout au long du titrage. En traçant la courbe $*\mathrm{pH} = f(V_\mathrm{titrant})*$, on peut facilement repérer, a posteriori, l’équivalence grâce à la méthode des tangentes.
TP Titrage de la soude par l’acide chlorhydrique
- Mettre en œuvre le suivi pH-métrique d’un titrage ayant pour support une réaction acide-base.
Présentation du TP
Vous allez déterminer la concentration d’une solution de soude $*\ce{(Na^+ +}*$ $*\ce{HO^-)}*$ (concentration attendue ≲ 0,4 g·L-1.).
Pour cela, vous disposer du matériel nécessaire au titrage, d’un pH-mètre et d’une solution d’acide chlorhydrique de concentration $*c_A*$ = 10,0 mmol·L-1.
Questions préalables
1. Quelle est l’équation-bilan de la réaction de titrage ?
2. Comparer la concentration de l’acide chlorhydrique et de la soude. Quel problème pourrait se poser ? comment le résoudre ?
3. Déterminer le volume de soude à doser une fois que vous avez résolu le problème éventuel soulevé à la question précédente.
4. Réaliser un schéma du montage expérimental comme vous l’avez appris dans le paragraphe précédent.
Travail demandé
- Réaliser le titrage de la soude par l’acide chlorhydrique, en mesurant le pH du mélange pour chaque ajout d’acide. Au début du dosage vous ferez une mesure pour chaque mL ajouté, mais lorsque vous arriverez près de l’équivalence supposée, vous ferez une mesure de pH pour chaque demi millilitre ajouté.
- Tracer le graphique $* \mathrm{pH} = f(V_A) *$ sur Excel.
Exploitation du graphique
- Utilisez la méthode des tangentes (dans la rubrique Divers > Méthodes &s techniques de TP) pour déterminer le volume d’acide ajouté à l’équivalence $*V_{AE}*$.
- En déduire la concentration de la solution de soude.
En êtes-vous bien sûr… ?
On va maintenant estimer l’incertitude sur la concentration de la soude. Pour ça, la seule incertitude que je vous donne est celle portant sur $*C_A*$ : $*\Delta C_A*$ = ± 0,2 mmol·L-1.
- Estimer les incertitudes portant sur $*V_A*$ et $*V_{BE}*$ en vous aidant notamment des indications sur la verrerie. Si besoin, allez vous rafraîchir la mémoire sur la partie Incertitudes.
- En déduire l’incertitude sur $*C_B*$ en utilisant les règles sur les incertitudes composées.
Éléments de réponses
1. $*\ce{H3O^+ + OH^- \rightarrow 2 H2O}*$
2.
3.
4. Voir cours. La soude est dans la burette et l’acide dans le bécher.
Dérivée du pH en fonction du volume de titrant versé
Vous pourrez voir, sur certains graphiques de suivi du pH, un deuxième courbe, en plus de $*\mathrm{pH} = f(V_\mathrm{titrant})*$. Il s’agit de la courbe représentant la dérivée du pH en fonction de $*V_\mathrm{titrant}*$ ajouté.
Lors d’un titrage pH-métrique, l’équivalence est le point de la courbe où le pH varie le plus fortement (en hausse ou en baisse).
Donc sur la courbe $* \dfrac{\mathrm{dpH}}{\mathrm{d}V} *$, l’équivalence sera repérable par le pic que présente cette courbe.
Exploitation du titrage
Dans le cas des titrages acide-base, on voit que les proportions stœchiométriques acide – base sont de 1 pour 1. À l’équivalence, on a mis autant de réactif titrant (en qdm) qu’il y avait initialement de réactif titré. On a donc la relation suivante à l’équivalence :
| $*C_1V_1=C_2V_{2E}*$ | $*C_1*$ : concentration molaire du titré (inconnue) $*V_1*$ : volume de titré (prélevé à la pipette jaugée) $*C_2*$ : concentration molaire du titrant (connue) $*V_{2E}*$ : volume de titrant versé à l’équivalence (déterminé expérimentalement). |
Titrage de l’acide lactique
On réalise le titrage pH-métrique d’une solution SA d’acide lactique $*\ce{H3C-CH(OH)-COOH}*$ par de la soude. La concentration massique de l’acide lactique attendue vaut 1,8 g·L-1 ± 10 %.
On dispose d’une solution de soude à la concentration $*C_B*$ = 3,00·10-2 mol·L-1.
1. Donner l’équation-bilan de la réaction de titrage. Vous noterez l’acide lactique $*\ce{AH}*$ dans cette équation.
2. Proposer un volume de solution d’acide lactique $*V_A*$ à doser de telle sorte que l’on soit sûr, si SA a bien la concentration attendue, que le volume de base versé à l’équivalence $*V_{BE}*$ soit compris entre 10 et 20 mL. Le volume $*V_A*$ doit pouvoir être prélevé avec une pipette jaugée (donc être égal à 5, 10, 15, 20 ou 25 mL).
On réalise le dosage de $*V_A*$ = 20 mL de SA par suivi pH-métrique. On obtient la courbe ci-dessous.
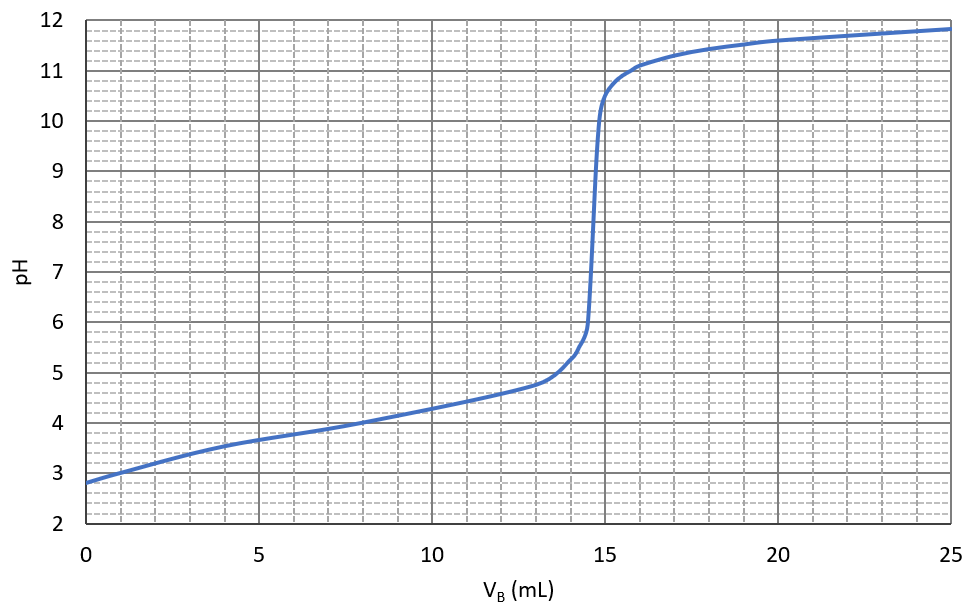
3. Déterminer le volume de soude versé à l’équivalence $*V_{BE}*$ par la méthode des tangentes (vous pouvez soit imprimer le graphique, soit le copier-coller dans un traitement de texte et faire votre construction sur ce document).
4. En déduire la concentration molaire $*C_A*$ de l’acide lactique, puis sa concentration massique $*C_{mA}*$.
Incertitudes
5. Estimer l’incertitude portant sur $*V_{BE}*$. On attend une incertitude absolue estimée « à la louche » mais de manière « intelligente » quand-même. 😊
L’incertitude sur le prélèvement de $*V_A*$ est de 0,05 mL. Celle sur la concentration $*C_B*$ est de 0,1 mmol·L-1.
6.a. Donner l’incertitude expérimentale portant sur $*C_A*$.
6.b. Est-on absolument sûr que la solution SA a bien la concentration attendue ?
Correction
1. $*\ce{AH + HO^- \rightarrow A^- + H2O}*$
2. La méthode la plus simple (mais pas le plus exhaustive) consiste à utiliser la concentration « moyenne » d’acide lactique (1,8 g·L-1) et le volume « moyen » souhaité à l’équivalence (15 mL). On calcule ensuite le volume d’acide $*V_A*$ nécessaire.
Concentration molaire en acide lactique : $*C_A*$ = 1,8÷90 = 20 mmol·L-1.
$*V_{A}*$ = 30×15÷20 = 22,5 mL. On va donc choisir de doser 20 mL d’acide (à cause du choix limité de pipettes jaugées disponibles).
On vérifie ensuite que ce choix de $*V_A*$ = 20 mL est compatible avec le volume de base versé à l’équivalence $*V_{BE}*$ souhaité.
Si l’acide à une concentration de 22 mmol·L-1 (20 mmol·L-1 + 10 %), on aura $*V_{BE}*$ = 22×20÷30 = 14,7 mL
Si l’acide à une concentration de 18 mmol·L-1 (20 mmol·L-1 – 10 %), on aura $*V_{BE}*$ = 18×20÷30 = 12 mL
On trouve donc bien un $*V_{BE}*$ compris entre 10 et 20 mL. Une remarque en passant, on aurait aussi pu choisir un volume $*V_A*$ = 25 mL et vérifier que ce volume est bien compatible avec les valeurs de $*V_{BE}*$ souhaitées (ce qui est le cas).
3. Par la méthode des tangentes, on trouve $*V_{BE}*$ ≃ 14,6 mL
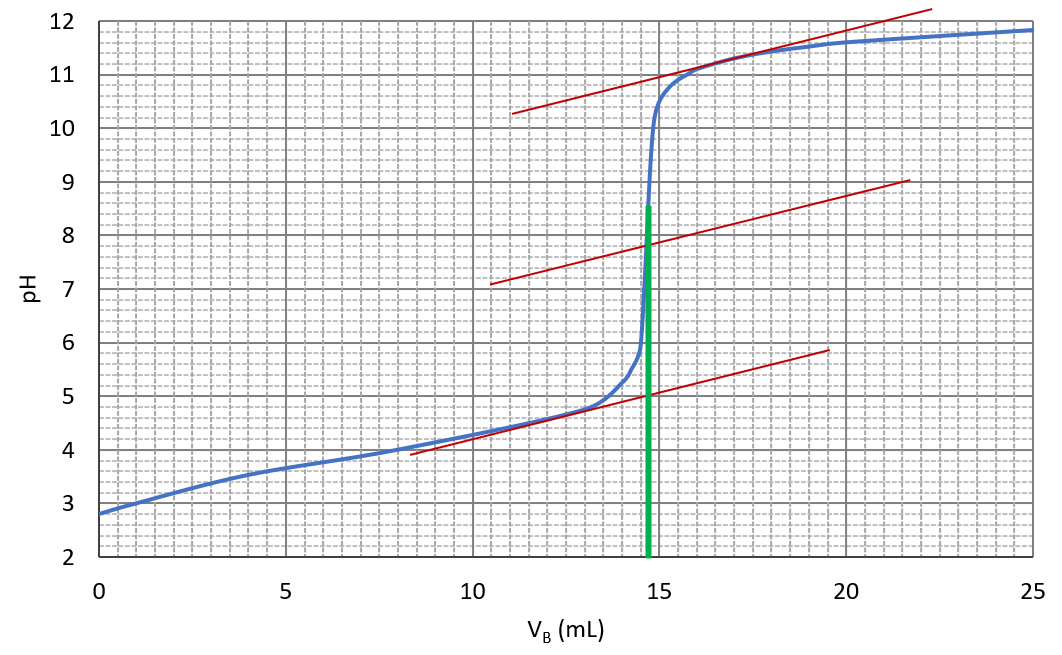
4. $*C_A*$ = 0,03×14,6÷20 = 21,9 mmol·L-1. Concentration massique $*C_{mA}*$ ≃ 1,97 g·L-1.
5. Graphiquement, on est sûr que 14,5 ≤ $*V_{BE}*$ ≤ 14,8. Donc $*V_{BE}*$ = 14,65 mL ± 0,15 mL. À cette incertitude on peut ajouter l’incertitude liée au réglage du « zéro » qui est de ± 0,05 mL (une demie plus petite graduation). Oui, je sais, j’ai oublié de vous en parler en cours 😊. On arrive à $*V_{BE}*$ = 14,65 mL ± 0,2 mL.
6.a. L’incertitude relative sur $*C_A*$ est la moyenne quadratique (ou géométrique) des incertitudes des grandeurs grâce auxquelles on la calcule. Donc : $µ \frac{\Delta C_A}{C_A} = \sqrt{ \left( \frac{\Delta C_B}{C_B} \right)^2 + \left( \frac{\Delta V_A}{V_A} \right)^2 + \left( \frac{\Delta V_B}{V_B} \right)^2} µ$ Donc $*\frac{\Delta C_A}{C_A}*$ = 0,014 (1,4%)
6.b. On a trouvé que $*C_A*$ = 1,97 g·L-1 ± 1,4%, donc 1,94 g·L-1 ≤ $*C_A*$ ≤ 2,00 g·L-1
Or la concentration attendue est comprise entre 1,62 et 1,98 g·L-1
Donc, d’après le résultat de nos expériences, on ne peut pas exclure que $*C_A*$ soit supérieur à 1,98 g·L-1 puisqu’il peut valeur jusqu’à 2,00 g·L-1. La réponse est donc non.
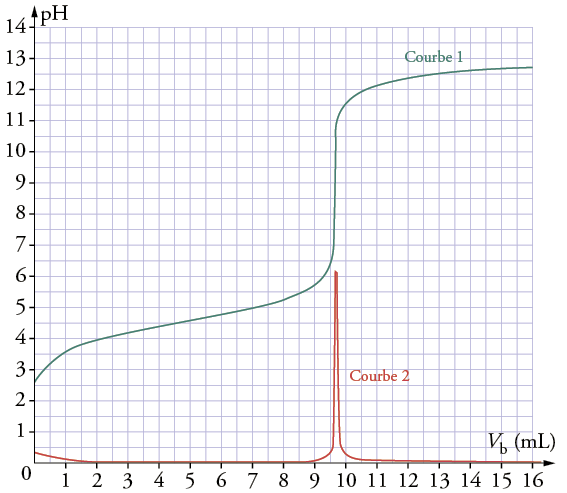
Titrage de l’acide ascorbique dans la vitamine C
D’après un exercice de bac Antilles 2014
L’acide acorbique est un acide faible organique qu’on notera $*\ce{AH}*$, de masse molaire 176 g·mol-1.
On souhaite vérifier l’indication figurant sur une boîte de comprimés de vitamine C vendue en pharmacie : de 500 mg d’acide ascorbique par comprimé.
Protocole
- Un comprimé de vitamine C est écrasé dans un mortier. La poudre est ensuite dissoute dans une fiole jaugée de 200,0 mL que l’on complète avec de l’eau distillée jusqu’au trait de jauge en homogénéisant le mélange. On obtient la solution S.
- On prélève 10,0 mL de cette solution que l’on titre avec une solution d’hydroxyde de sodium de concentration molaire $*c_B*$ 10,0 mmol·L-1.
- On suit le titrage par pH-métrie et on obtient le graphique ci-dessous.
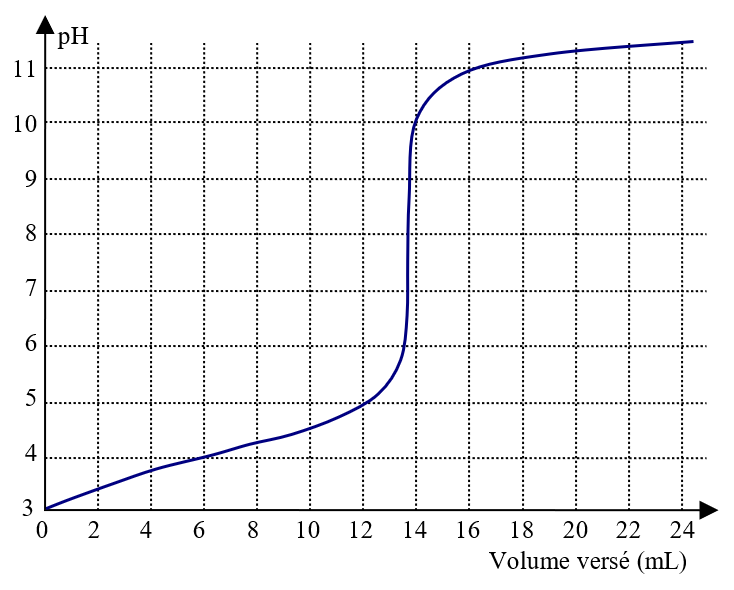
Évolution du pH en fonction du volume de solution d’hydroxyde de sodium versé
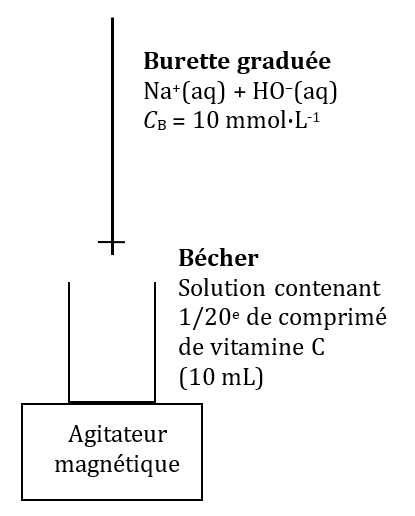
1. Réaliser un schéma annoté du montage expérimental nécessaire à la mise en œuvre du titrage.
2. Écrire l’équation de la réaction support du titrage.
3. Déterminer la masse d’acide ascorbique contenue dans le comprimé.
4. Calculer l’écart relatif entre la masse théorique et la masse expérimentale.
5. L’incertitude sur les 10 mL de solution d’acide ascorbique prélevée est de ± 0,05 mL, L’incertitude sur $*c_B*$ est de ± 1 %. Estimer l’incertitude sur $*V_{BE}*$ et calculer l’incertitude sur la masse d’acide ascorbique contenue dans le comprimé.
Que peut-on conclure quant à l’exactitude de l’indication du fabriquant ?
Correction
1. Schéma annoté du montage expérimental
2. $*\ce{AH + HO^- \rightarrow A^- + H2O}*$
3. On détermine d’abord $*V_{BE}*$ ≃ 13,8 mL (méthode des tangentes, non détaillées ici)
$*n_A*$ = $*C_B×V_{BE}*$ = 10×13,8 = 138 µmol, soit une masse $*m_A*$ = 138·10-6×176 = 24,3 mg pour 1/20e de comprimé.
Donc pour un comprimé : 486 mg
4. Écart relatif : (500-486)÷500 = 0,028 (2,8 %).
5. $*\Delta V_{BE}*$ = ± 0,25 mL (la lecture graphique n’est pas évident, mais on est sûr d’être entre 13,5 et 14 mL)
En calculant la moyenne géometrique des incertitudes relatives sur $*V_A*$, $*C_B*$ et $*V_{BE}*$, on trouve une incertitude relative sur $*C_A*$ de ± 1,6 %. $*m_A*$ et $*C_A*$ étant proportionnelles, on a la même incertitude relative sur $*m_a*$, donc $*m_a*$ = 486 mg ± 10 mg.
Malgré l’incertitude de ce titrage, on peut être sûr que le fabriquant a légèrement exagéré son indication.
Titrage conductimétrique
- Dans le cas d’un titrage avec suivi conductimétrique, justifier qualitativement l’évolution de la pente de la courbe à l’aide de données sur les conductivités ioniques molaires.
Si la réaction de titrage implique des ions, il est possible de suivre cette réaction (et donc de répérer l’équivalence) par conductimétrie.
Rappelez-vous la loi de Kohlrausch :
| $* \sigma = \sum_i \lambda_i·[\mathrm{X}_i] *$ |
$*\lambda_i*$ : conductivité ionique molaire de l’ion $*\mathrm{X}_i*$ $*[\mathrm{X}_i]*$ : concentration de l’ion $*\mathrm{X}_i*$ |
Cette loi nous dit que la conductivité $*\sigma*$ d’une solution dépend de la nature des ions qu’elle contient et de leur concentration. Si l’une et/ou l’autre change, la conductivité change.
C’est le cas pour une réaction acide-base, par exemple : lors de la réaction $*\ce{AH + HO^- \rightarrow A^- + H2O}*$, des ions $*\ce{HO^-}*$ sont consommés et des ions $*\ce{A^-}*$ apparaîssent.
TP Titrage de la soude par l’acide chlorhydrique
- Mettre en œuvre le suivi conductimétrique d’un titrage.
Présentation du TP
On va faire la même chose que dans le TP précédent : déterminer la concentration d’une solution de soude par de l’acide chlorhydrique $*\ce{(H3O^+ +}*$ $*\ce{Cl^-)}*$. La concentration attendue de la soude est de (0,10 ± 0,01) mol·L-1. Vous disposez d’une solution d’acide chlorhydrique à 0,100 mol·l-1
Mais à la place du pH-mètre, on utilisera un conductimètre.
Travail demandé
- Déterminer quel volume de soude il est pertinent de doser si on veut que $*V_{AE}*$ ≃ 15 mL.
- Attention, lisez bien ce qui suit : vous rajouterez environ 100 mL d’eau distillée au volume de base que vous avez prélevé (du coup, pensez à prendre un bécher assez grand).
- Réaliser le titrage de la soude par l’acide chlorhydrique, en mesurant la conductivité du mélange pour chaque ajout de base. Vous ferez une mesure pour chaque mL ajouté, jusqu’à avoir dépassé l’équivalence prévue d’au moins 10 mL.
- Tracer le graphique $* \sigma = f(V_B) *$ sur Excel.
Exploitation du graphique
Utilisez votre 🧠 (et les données de conductivité des différents ions) pour :
- comprendre pourquoi le graphique a cette forme ;
- comprendre comment repérer l’équivalence (et pourquoi on peut faire comme ça) ;
- en déduire la concentration de l’acide.
Conductivités ioniques molaires
$*\lambda_\ce{HO^-}*$ = 20 mS·m2·mol-1$*\lambda_\ce{H3O^+}*$ = 35 mS·m2·mol-1
$*\lambda_\ce{Na^+}*$ = 5,0 mS·m2·mol-1
$*\lambda_\ce{Cl^-}*$ = 7,6 mS·m2·mol-1
- Dernière question assez subtile : pourquoi ajouter 100 mL d’eau distillée dans l’acide à doser ? Vous pouvez tester sur le tableur ce que donne la courbe simulée $*\sigma = f(V_B)*$ si on ne dilue pas l’acide à titrer.
En êtes-vous bien sûr… ?
Estimer l’incertitude sur la concentration de l’acide. Vous commencez à être habitué, je n’en dis pas plus, débrouillez-vous 😊
Éléments de réponses
Allure de la courbe de titrage
La représentation graphique de $*\sigma = f(V_B)*$ est l’association de deux droites (si l’effet de la dilution sur le dosage est négligeable – sinon, ces droites tendent à se courber). L’équivalence est repérable au moment du changement de pente.
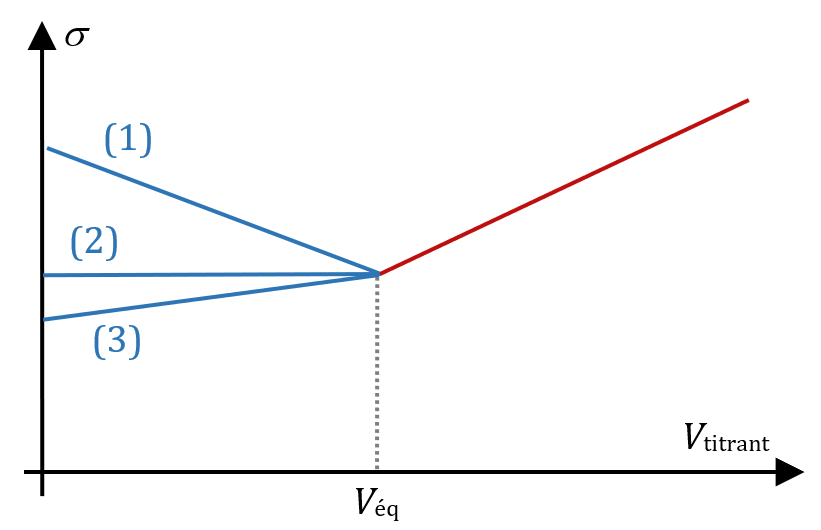
Le segment de droite avant l’équivalence peut être décroissant (1), constant (2) ou croissant (3) : ça dépend de la réaction de titrage et de la conductivité des ions présents lors du titrage (y compris des ions spectateurs). Par contre, après l’équivalence, la conductivité est toujours croissante car on ne fait qu’ajouter les ions contenus dans le titrant.
Il vous faut savoir justifier l’allure de la courbe dans le cas où la variation du volume de la solution titrée est négligeable (autrement dit, la solution titrante doit être beaucoup plus concentrée – ce qui sera toujours le cas).
Lorsque le volume de solution titrante versé n’est pas négligeable devant le volume total de solution contenu dans le bécher où on réalise le titrage, l’effet de la dilution sur la conductivité du mélange a tendance à « courber » les deux droites, rendant la détermination de l’équivalence moins précise.
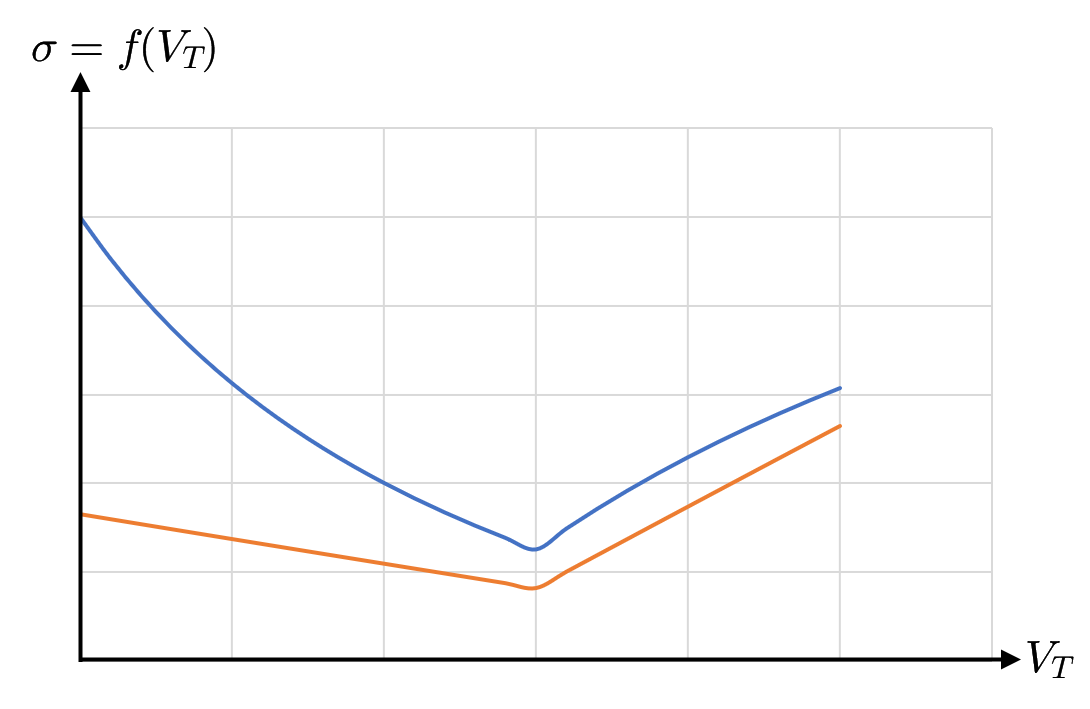
Exemple du titrage de l’acide chlorhydrique par la soude
C’est l’exemple que nous avons vu en TP. Au départ, dans le bécher contenant la solution titrée – c’est-à-dire l’acide chlorhydrique – il y a des ions oxonium $*\ce{H3O^+}*$ et des ions chlorure $*\ce{Cl^-}*$.
Avant l’équivalence : pour chaque ion hydroxyde introduit dans le bécher, on introduit également un ion sodium. Bien sûr, cet ion ne participe pas à la réaction, mais il a une influence sur la conductivité de la solution… l’ion hydroxyde réagit avec l’ion oxonium $*\ce{H3O^+ + HO^- \rightarrow 2 H2O}*$. Donc en terme d’ion, ça revient à remplacer un ion oxonium par un ion sodium. Or, les ions oxonium sont de bien meilleurs conducteurs que les ions sodium ($*\lambda_\ce{H3O^+}*$ = 35 mS·m2·mol-1 et $*\lambda_\ce{Na^+}*$ = 5,0 mS·m2·mol-1). Donc la conductivité de la solution diminue.
Après l’équivalence : On ne fait qu’ajouter des ions $*\ce{HO–}*$ et $*\ce{Na+}*$, donc la conductivité augmente.
Titrage des ions chlorure
Un exemple classique de titrage par suivi conductimétrique est celui des ions chlorure. Le titrant est une solution de nitrate d’argent $*\ce{(Ag^+ + NO3^- )}*$.
Le chlorure d’argent $*\ce{AgCl}*$ est quasi-insoluble dans l’eau. Du coup, lorsqu’on verse du nitrate d’argent dans une solution contenant des ions chlorure, on obtient la réaction totale et rapide : $µ \ce{Ag^+(aq) + Cl^-(aq) \rightarrow AgCl(s)} µ$
On dose 15,0 mL d’une solution S de chlorure de sodium par une solution S’ de nitrate d’argent de concentration $*C_{na}*$ = 15 mmol·L-1. On a préalablement rajouté environ 100 mL d’eau distillée aux 15 mL de solution S.
Les mesures de conductivité sont rassemblées dans ce fichier texte.
Conductivités ioniques molaires
$*\lambda_\ce{NO3^-}*$ = 7,1 mS·m2·mol-1
$*\lambda_\ce{Cl^-}*$ = 7,6 mS·m2·mol-1
1. En déduire la concentration de S.
2. Justifier l’allure du graphique obtenu.
3. Expliquer pourquoi on dilue S avec un grand volume d’eau distillée.
4. L’incertitude sur la concentration en nitrate d’argent est de ±1 %. Estimer l’incertitude sur le volume équivalent sachant que le 0 de la burette est reglé à ±0,05 mL (il faut aussi estimer l’incertitude sur la détermination graphique du volume équivalent). L’incertitude sur le volume de S dosé est de 0,5 %. En déduire l’incertitude sur la concentration de S.
Correction
1. Il faut d’abord tracer le graphique $*\sigma = f(V_{S’})*$.
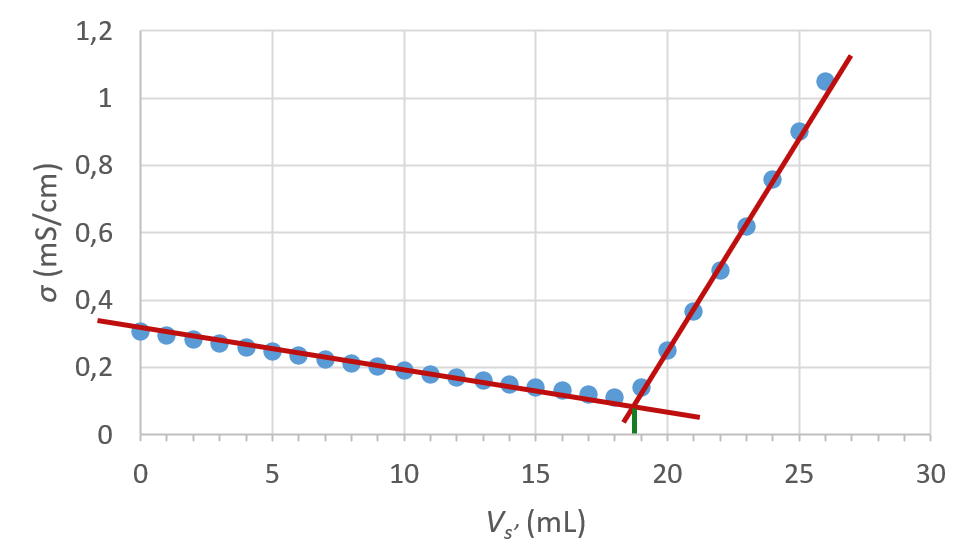
On trouve un volume à l’équivalence de $*V_{S’E}*$ = 18,8 ou 18,9 mL.
Qdm d’ions $*\ce{Ag^+}*$ introduits à l’équivalence : $*n_{\ce{Ag^+}E}*$ = 18,85×15 = 280 µmol environ.
Étant donné les nombres stœchiométriques de la réaction, on en déduit que $*n_{\ce{Cl^-}i}*$ = 280 µmol.
D’où $*\ce{[Cl^-]}_i*$ ≃ 19 mmol·L-1.
2. Avant l’équivalence, les ions chlorure réagissent et sont remplacés par des ions nitrate. Or $*\lambda_{\ce{NO3^-}}*$ < $*\lambda_{\ce{Cl^-}}*$, donc la conductivité de la solution diminue.
Après l’équivalence, on ne fait qu’ajouter des ions $*\ce{Ag^+}*$ et $*\ce{NO3^-}*$ à la solution, dons sa conductivité augmente.
3. Ça permet de négliger l’effet de la dilution sur la conductivité de la solution. Celle-ci ne varie qu’à cause de la variation de la qdm des différents ions. On obtient ainsi un graphique formé de deux segments de droite, où l’équivalence peut être repérée de manière plus précise.
4. Par lecture graphique, on est sûr que le volume équivalent est compris entre 18,6 et 19 mL (±0,2 mL). En comptant que le 0 est fait à ± 0,1 mL, ça nous fait une incertitude totale de ±0,25 mL sur le volume à l’équivalence. $µ \frac{\Delta C_S}{C_S} = \sqrt{\left(\frac{\Delta V_S}{V_S}\right)^2 + \left(\frac{\Delta V_E}{V_E}\right)^2 + \left(\frac{\Delta C_{na}}{C_{na}}\right)^2} µ$ On trouve $* \dfrac{\Delta C_S}{C_S} *$ = 1,7 %
Révision & entraînement
Titrage d’une solution de soude
On dispose de soude solide $*\ce{NaOH(s)}*$ qui a été soumise à l’humidité de l’air. On souhaite déterminer quel est le pourcentage massique en eau de cette soude « hydratée ». On estime que ce pourcentage massique est compris entre 0 et 5 %.
À partir de 1,00 g de cette soude, on réalise 250,0 mL de solution.
On dispose d’acide chlorhydrique ($*\ce{H3O+ + Cl–}*$) de concentration 0,100 mol·L-1, de pipettes jaugées (5, 10, 15, 20 et 25 mL) d’une burette graduée de 25 mL, d’un agitateur magnétique et d’un pH-mètre étalonné.
Données
- Masse molaire de la soude $*M(\ce{NaOH})*$ = 40,0 g·mol-1
- Incertitude relative sur une grandeur calculée : si $*a = \dfrac {bc}d*$, alors : $* \dfrac {\Delta a}a = \sqrt{\left(\dfrac {\Delta b}b\right)^2 + \left(\dfrac {\Delta c}c\right)^2 + \left(\dfrac {\Delta d}d\right)^2} *$
1. Donner l’équation-bilan de la réaction de titrage.
2. Proposer un volume de solution de soude à doser sachant que l’on veut avoir un volume d’acide chlorhydrique versé à l’équivalence voisin de 15 mL. Justifier votre réponse par les calculs nécessaires.
On réalise le dosage de 15 mL de cette solution de soude par l’acide chlorhydrique décrit en début d’énoncé. On obtient la courbe suivante.
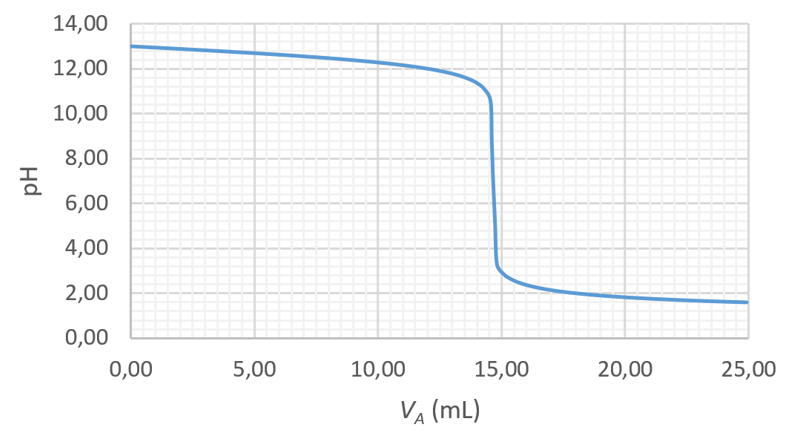
3. En déduire le pourcentage massique d’eau contenue dans la soude utilisée.
L’incertitude sur la concentration de l’acide chlorhydrique est de ± 0,5 %. L’incertitude sur la mesure du volume de base prélevée est de ± 0,05 mL.
4.1. Estimer l’incertitude sur le volume d’acide versé à l’équivalence.
4.2. Calculer l’incertitude relative sur la concentration de la soude.
4.3. Sachant que l’incertitude sur la masse de soude pesée est de ± 0,005 g, pensez-vous que la précision du pourcentage d’eau trouvé grâce à ce titrage soit satisfaisante ?
Correction
1. $*\ce{HO– + H3O+ \rightarrow 2 H2O}*$
2. On s’attend à une concentration de la soude comprise entre 0,100 et 0,095 mol·L-1.
Donc le volume d’acide versé à l’équivalence $*V_{AE}*$ sera compris entre $*V_B*$ et 1,05$*V_B*$. Si on dose $*V_B*$ = 15,0 mL, on est sûr d’avoir un volume compris entre 15 mL et 14,25 mL, ce qui satisfait aux exigences.
3. Volume à l’équivalence (méthode des tangentes) : entre 14,55 et 14,6 mL.
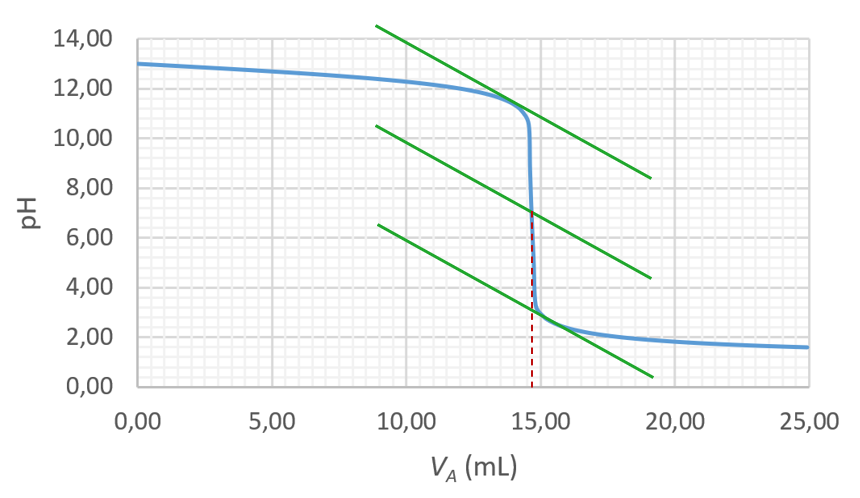
Il y a une quantité de matière $*n_B*$ = $*C_A·V_{AE}*$ = 0,10×14,55 = 1,455 mmol de soude dans les 15 mL de solution dosée. Donc il y a 1,455×250÷15 = 24,25 mmol de soude dans les 250 mL de solution réalisée. Ça représente 0,97 g de soude (pour 1,00 g pesé). C’est donc qu’il y a 0,03 g d’eau et donc que la teneur massique en eau de la soude est de 3 %.
4.1. En tenant compte d’une incertitude de ± 0,05 mL sur le réglage du zéro et de l’incertitude de lecture sur la courbe, on est sur que $*V_{AE}*$ est compris entre 14,45 mL et 14,80 mL. Qu’on peut encore écrire : 14,625 mL ± 0,175 mL et qu’on peut arrondir à 14,63 ± 0,18 mL.
4.2. Il faut calculer l’incertitude relative sur $*V_{AE}*$ : ± 1,2 % et l’incertitude relative sur $*V_B*$ : 0,33 %
Donc : $* \dfrac{\Delta C_B}{C_B} = \sqrt{0,012^2 + 0,0033^2 + 0,005^2}*$ = 0,0134
L’incertitude relative sur $*C_B*$ est de 1,34 % (qu’on peut arrondir à 1,4 %).
4.3. Sachant qu’on a trouvé qu’il y a 0,03 g d’eau dans cette soude est qu’on est à ± 0,005 g, ça fait une incertitude relative sur la masse d’eau de près de 17 %. Ce n’est pas très satisfaisant.
Autre manière de faire
On est sûr d’avoir pesé au minimum 0,995 g d’eau, pour lesquels il y a 0,97 g de soude. Ça fait un pourcentage massique d’eau de 2,5 % environ.
On est sûr d’avoir pesé au maximum 1,005 g d’eau, pour lesquels il y a 0,97 g de soude. Ça fait un pourcentage massique d’eau de 3,5 % environ. Donc le pourcentage massique est de (3±0,5) %.
Remarque
Pour être rigoureux, il faudrait qu’on tienne également compte de l’incertitude sur la détermination de CB (1,4 %).
Dans le pire des cas, on a 98,6 % de 0,97 g (soit 0,956 g) de soude pure pour une masse totale de 1,005 g (soit 0,049 g d’eau).
Dans le meilleur des cas, on a 101,4 % de 0,97 g (soit 0,98 g) de soude pure pour une masse totale de 0,995 g (soit 0,015 g d’eau).
En tenant compte de toutes les incertitudes, on a donc entre 1,5 % et 4,9 % d’eau. C’est encore moins précis.
Mais je n’en attendais pas autant en devoir. 😅
Titrage acide-base par suivi pH-métrique
Cet exercice a été donné en devoir en 2020/2021
On dose une solution d’acide faible $*\ce{AH}*$ de concentration attendue $*C_A*$ = 0,10 mol·L-1 ± 10 % par de la soude à 60 mmol·L-1.
1. Donner l’équation-bilan de la réaction de titrage
2. Proposer un volume d’acide à doser pour avoir un volume de base versée à l’équivalence $*V_{BE}*$ voisin de 15 mL.
3.a. Le volume trouvé à l’équivalence est de $*V_{BE}*$ = 13,8 mL pour un volume d’acide dosé $*V_A*$ = 10 mL.
Trouver la concentration de la solution d’acide dosée, ainsi que l’incertitude qui lui est associée.
Données
- Incertitude sur $*V_A*$ : négligeable
- Incertitude sur $*C_B*$ : ± 2 %
- Incertitude sur $*V_{BE}*$ : ± 0,2 mL
3.b. Ce résultat est-il compatible avec la concentration attendue ? Justifier.
Correction
1. $*\ce{AH + HO– → A– + H3O+}*$
2. $* V_A = \dfrac {C_B V_{BE}}{C_A} *$ = 0,06×15÷0,1 = 9 mL. Il faut donc doser 10 mL.
3.a. $* C_A = \dfrac {C_B V_{BE}}{V_A} *$ = 0,060×13,8÷10 = 8,28·10-2 mol·L-1
Incertitude relative sur $*C_A*$ : $* \dfrac {\Delta C_A}{C_A} = \sqrt{\left( \dfrac {ΔC_B}{C_B} \right)^2 + \left( \dfrac {ΔV_{BE}}{V_{BE}} \right)^2 }*$= 2,5 %
Donc $*C_A*$ = (0,083 ± 0,002) mol·L-1
3.b. On s’attend à une concentration comprise entre 0,090 et 0,110 mol·L-1. On a trouvé une concentration comprise 0,081 et 0,085 mol·L-1, donc ce n’est pas compatible avec la concentration attendue.